Heron method
The Heron method , Heron's approximation method or Babylonian root extraction is a calculation method for calculating an approximation of the square root of a real number .
Procedure
The iteration equation of the Heron method can be derived from the Newton method for the zero of the quadratic function . With results from the recursion formula of Newton's method , the iteration :
- .
As long as it is not equal to zero, the start value of the iteration can be set arbitrarily; the iteration always converges. It should be noted that with negative starting values, the iteration converges to the negative square root. A qualified estimate for the starting value is obtained from the Taylor series expansion of the binomial series by 1, the first two terms of which provide this equation:
The Heron method is one of the fixed point methods . If one sets , then applies to the fixed point (which fulfills the condition ) with the (positive) solution .
example
In the following simple example, the square root of 9 is shown as an approximation with three calculation steps to the true value . With the start value for the iteration is calculated and inserted into the iteration rule:
convergence
The procedure can be expressed as a recursively defined sequence as follows:
- .
It is a purely positive consequence. One can now show that the -th term is for all of them . To do this, one shows the equivalent inequality :
- .
We also show that a monotonically decreasing sequence is:
- .
Due to the limitedness and monotony shown, the sequence must converge, from above to the root sought:
- .
Since the Heron method can be derived from Newton's approximation method and the zero to be calculated is simple, the order of convergence is 2.
The method converges very quickly if there is already a good approximation. The number of correct digits is roughly doubled with each step. However, if the first approximation is bad, it takes many steps to get a good approximation.
For example, if the root is to be calculated from an integer with 200 binary digits and you start with the first approximation, then the approximation becomes about one binary digit shorter with each step, i.e. approx. H. only after about 100 steps does the approximation have the correct length of 100 places. Then six to seven more steps ( ) are sufficient to correctly calculate all 100 places before the decimal point.
It is therefore advisable to determine a starting value that is as precise as possible . In the example, you should first determine the bit length of and use a start value with half the length.
Error estimation
The following applies to the Heron sequence :
- (Inclusion),
and the following estimate for the error
This error estimation has the disadvantage that it is not known but should be calculated. Using the above inclusion, the following workable estimate is obtained:
- .
Applied to the above example one obtains:
- .
For the relative error
the recursion applies
- .
The consequence of is therefore independent of the starting approximation for a given relative error .
Geometric illustration of the Heron process
The Heron method is based on the idea that a square with area has a side length of . The starting point of the procedure is any rectangle with area . Step by step, the aspect ratio of the rectangle is changed so that its shape more and more approximates that of a square, while the area remains the same. The side lengths of the rectangle are the approximate values for .
In the first step any side length is chosen for the rectangle. So that this has the desired area, the second side length is calculated using the formula
calculated. As an example, the square root of 9 should be calculated. The value 9 is selected for one side length, so that the other side length is calculated as 1. The first rectangle therefore has the following shape.
The resemblance of this rectangle to a square is little. This is also expressed by the fact that the side lengths 1 and 9 are very poor approximations for the root of 9.
To get a better approximation of a square, the long side needs to be shortened and the short side lengthened. The new length of the long side becomes the mean
of the two previous side lengths taken. The length of the other side is calculated as above
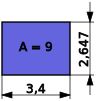
In the example, the average side length is 5. The corresponding short side has a length of 1.8.
Here, too, the resemblance to a square is still small. However, the new rectangle is more compact compared to the previous one.
The process described is repeated in every further step of the Heron process. The mean value of the side lengths of a rectangle corresponds to the length of the long side of the new rectangle and the length of the short side can be calculated from this as described above. In the example, the following two rectangles are created in the next two steps.
The last rectangle is almost square. The side length of 3.024 is accordingly close to 3, the exact value of .
Implementation in software
The method is particularly suitable for implementation in software, since only basic arithmetic operations are required, so it is rarely needed today in view of the wide availability of numerical processor hardware.
If a floating point representation with a two-way exponent is also used, the approach becomes relatively simple, as an example , the root of 5 is considered and the relative error to the final value (i.e. abs ((x i - x) / x)) is followed:
- First an even number is split off from this two-way exponent, so that either a 0 or 1 remains as the exponent, ie the number is normalized to the interval [½, 2] . In this interval the square root function is only a slightly curved curve, so it can be treated numerically well. Example: For the time being, only a = 1.25 with the goal x = 1.118034 will be treated.
- As a starting value for the actual iteration, this curve is approximated by an even simpler one that can be calculated directly (without iteration). This initial calculation is used to determine the starting value with which the following iteration is started. This curve can be applied more or less laboriously, with the increasingly complicated approaches below, one iteration step can be saved if necessary:
- a simple constant (for example 1), for
example: x 0 = 1; rel. Error = 1.1 * 10 −1 ; - a straight line with a gradient of 1/2 and an additive constant of 1/2 (to simplify the following case),
example: x 0 = 1/2 + 1.25 / 2 = 1.125; rel. Error = 6.2 * 10 −3 ; - a straight line with a gradient of 1/2 and an additive, optimized constant of , example: x 0 = 0.929683 / 2 + 1.25 / 2 = 1.089841; rel. Error = 2.5 * 10 −2 ;
- a straight line with an optimized slope and an additive constant (not considered here).
- a simple constant (for example 1), for
- A fixed number of iteration steps is carried out on the basis of the start value x 0 determined in this way . The number required to achieve the desired accuracy can be calculated directly as the worst case within the start interval thanks to the above error estimate. For example, with a 32-bit mantissa and the middle starting point, you only need three steps. This fixed number saves considerably more time-consuming queries to achieve accuracy. Replacing the mentioned constants with the number 1.0 does not change this. Even the even more complicated approach would not save a further iteration step, at least with this accuracy. It can look different with higher accuracy requirements.
Example with three steps according to approach 1 (constant 1, with the other approaches it converges one step faster):
x 1 = (x 0 + a / x 0 ) / 2 = (1 + 1.25 / 1) / 2 = 1.125; rel. Error = 6.2 * 10 −3
x 2 = (x 1 + a / x 1 ) / 2 = (1.125 + 1.25 / 1.125) / 2 = 1.118056; rel. Error = 2.0 * 10 −5
x 3 = (x 2 + a / x 2 ) / 2 = (1.118056 + 1.25 / 1.118056) / 2 = 1.118034; rel. Error = 0
You can see the effect of the quadratic convergence, that the error is squared from step to step or the number of valid digits or the negative error exponent roughly doubles. - Finally, the exponent is restored by adding half of the value split off in the first step.
Example: x = 2 * x 3 = 2.236068.
Generalization of the procedure
This procedure can be generalized so that for is calculated. The larger is, the more steps are needed to accurately calculate the root.
The Newton method is used to determine the positive zero of the function . The iteration rule follows from the recursion formula of Newton's method :
Here the sequence has to be started with a suitable starting value for the searched value of .
The same convergence statements apply to positive integers as above for
Determination of the reciprocal
For one obtains a procedure with which (without using the division!) The reciprocal value can be calculated approximately:
This procedure converges to the quadratic for all
For the first computers without built-in division, iteration made it possible to reduce this operation to multiplication and subtraction. The division of two numbers was carried out in such a way that the reciprocal of the denominator was determined and multiplied by the numerator.
example
It should be calculated approximately with the start value :
For the start value one gets
thus no convergence to the sought value of
Historical
The method was already known in Mesopotamia at the time of Hammurapi I (approx. 1750 BC), a king of Babylon . It was described by Heron of Alexandria in the first book of his work Metrica around 100 AD .
literature
- Bernd Ziegenbalg: Algorithms: From Hammurapi to Gödel . Harri Deutsch Verlag 2007, ISBN 978-3-8171-1814-4 , pp. 54-59.
- David Fowler, Eleanor Robson : Square Root Approximations in Old Babylonian Mathematics (PDF; 215 kB). Historica Mathematica 25, 1998, pp. 366-378.
- Hans R. Schwarz, Norbert Köckler: Numerical Mathematics. 6th edition. Teubner, Stuttgart 2006, ISBN 3-519-42960-8 , pp. 189-192.
Web links
- The Heron method for calculating the roots on arndt-bruenner.de (explanation and example calculator)
Remarks
- ↑ Start value: If the output value is already available as a binary number (in the place value system), you can simply count where its highest value '1' is; Start value is then . If the output value is in (binary) exponential notation, the exponent can simply be halved as the start value (shift by 1 bit to the right). See also section Implementation in software
Individual evidence
- ↑ Suitable transformations: zeros and fixed points. In: Montanuniversität Leoben . February 23, 2005, accessed August 27, 2019 .
- ↑ Bernd Ziegenbalg: Algorithms: From Hammurapi to Gödel . Harri Deutsch Verlag 2007, ISBN 978-3-8171-1814-4 , p. 54 ( excerpt (Google) )
- ↑ John J. O'Connor, Edmund F. Robertson : Heron method. In: MacTutor History of Mathematics archive .















































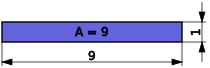






![\ left (2 \ cdot {\ sqrt [{4}] {2}} - {\ sqrt {2}} \ right) ^ {2} / 2 \ approx 0 {,} 4648415](https://wikimedia.org/api/rest_v1/media/math/render/svg/db61bf11555d17d421ce860273076e41e035893a)
![{\ sqrt [{k}] {a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eb8365e5cc7e07cd1dd14623222d5d03c556d6c)






![{\ sqrt [{- 1}] {a}} = 1 / a](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec3b09908cabfff51c3fc04a74f7f76d27a6aaf)













