Fixed point iteration

A fixed point iteration (or a fixed point method ) is a numerical method in mathematics for the approximate determination of solutions to an equation or a system of equations . The equation must first be converted into a fixed point equation, i.e. into an equation of the form

${\displaystyle \varphi (x)=x}$

can be transformed with a function . A starting approximation is then selected and calculated. The result is put back into the function , and so on. Under appropriate conditions, the additive thus obtained approaches result a solution of and thus a solution of the original problem on and on. ${\displaystyle \varphi }$ ${\displaystyle x_{0}}$ ${\displaystyle x_{1}=\varphi (x_{0})}$ ${\displaystyle \varphi }$ ${\displaystyle x_{2}=\varphi (x_{1})}$ ${\displaystyle x_{0},x_{1},x_{2},\dotsc }$ ${\displaystyle \varphi (x)=x}$

General procedure

Let there be a function that maps a set in itself, as well as a starting element . The sequence in generated by the associated fixed point method is then iteratively defined by ${\displaystyle \varphi \colon M\to M}$ ${\displaystyle M}$ ${\displaystyle x_{0}\in M}$ ${\displaystyle (x_{k})_{k\in \mathbb {N} _{0}}}$ ${\displaystyle M}$

${\displaystyle x_{k+1}=\varphi (x_{k})}$   for . ${\displaystyle k\in \mathbb {N} _{0}}$

If there is a concept of convergence on the set , one can ask whether this sequence converges to a fixed point of , that is, to a with . The Banach fixed point theorem indicates relatively general conditions under which this is the case: Is a complete metric space, so for example, a closed subset of or a Banach space , and a contraction , then there exists in the set exactly one fixed point of and through the fixed point method generated sequence converges for arbitrary against . ${\displaystyle M}$ ${\displaystyle \varphi }$ ${\displaystyle x^{*}}$ ${\displaystyle \varphi (x^{*})=x^{*}}$ ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \varphi }$ ${\displaystyle M}$ ${\displaystyle x^{*}}$ ${\displaystyle \varphi }$ ${\displaystyle x_{0}\in M}$ ${\displaystyle x^{*}}$

Examples

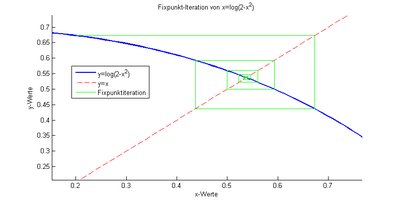
Graphical representation of the one-dimensional fixed point iteration

Find the positive solution to the equation

${\displaystyle 2-x^{2}=e^{x}}$.

By taking logarithms we obtain the fixed point equation

${\displaystyle \ln(2-x^{2})=x}$.

The iteration function given by , for example, maps the interval in itself and is on a contraction (see adjacent figure). ${\displaystyle \varphi (x)=\ln(2-x^{2})}$ ${\displaystyle M=[0{,}2;0{,}7]}$ ${\displaystyle M}$

Starting from the initial value is obtained for the next iteration , , etc. In the approximation after 20 steps already the first four digits correspond to the exact solution. ${\displaystyle x_{0}=0{,}2}$ ${\displaystyle x_{1}=\varphi (x_{0})\approx 0{,}6729}$ ${\displaystyle x_{2}=\varphi (x_{1})\approx 0{,}4364}$ ${\displaystyle x_{3}=\varphi (x_{2})\approx 0{,}5931}$ ${\displaystyle x_{20}\approx 0{,}5373}$

The Heron method also represents a fixed point iteration. For the function has the (positive) fixed point , so that it can be used for the numerical determination of . ${\textstyle a>0}$ ${\textstyle \varphi (x)={\frac {1}{2}}\cdot \left(x+{\frac {a}{x}}\right)}$ ${\textstyle x={\sqrt {a}}}$ ${\textstyle \varphi (x)}$ ${\textstyle {\sqrt {a}}}$

A sentence about existence and uniqueness

Let be a continuously differentiable fixed point iteration function with and for all off . Then there is exactly one fixed point from with . ${\displaystyle f\colon [a,b]\to [a,b]\subset \mathbb {R} }$ ${\displaystyle f(a)>a,f(b)<b}$ ${\displaystyle f'(x)\neq 1}$ ${\displaystyle x}$ ${\displaystyle (a,b)}$ ${\displaystyle x^{*}}$ ${\displaystyle (a,b)}$ ${\displaystyle f(x^{*})=x^{*}}$

proof

You bet . Then is . From the intermediate value theorem it follows that there is at least one zero with . If there were a second zero, for example , then there would have to be a point from the interval with according to Rolle's theorem , which implies contradicting the assumption. So the fixed point is clear. ${\displaystyle F(x):=f(x)-x}$ ${\displaystyle F(a)>0,F(b)<0}$ ${\displaystyle x^{*}\in [a,b]}$ ${\displaystyle F(x^{*})=0}$ ${\displaystyle x^{**}}$ ${\displaystyle F(x^{*})=F(x^{**})}$ ${\displaystyle {\check {x}}}$ ${\displaystyle (x^{*},x^{**})}$ ${\displaystyle F'({\check {x}})=0}$ ${\displaystyle f'({\check {x}})=1}$ ${\displaystyle x^{*}}$

example

The following applies to the function : ${\displaystyle f(x)={\frac {x^{3}-1}{x^{3}-2}}}$ ${\displaystyle [-1,+1]}$

• ${\displaystyle f(-1)>0>-1}$.
• ${\displaystyle f(+1)=0<1}$.
• ${\displaystyle f'(x)={\frac {-3x^{2}}{(x^{3}-2)^{2}}}\neq 1}$for everyone . ${\displaystyle x\in (-1,+1)}$

From this it follows from the sentence above that in has exactly one fixed point ( ). ${\displaystyle f}$ ${\displaystyle (-1,+1)}$ ${\displaystyle x^{*}\approx 0{,}4722129517}$

Linear fixed point method

Construction idea

The splitting method is an important special case of fixed point iteration . A system of linear equations

${\displaystyle Ax=b}$

with a non-singular n × n - matrix and a vector to transform into a fixed point equation, it decomposes the matrix by means of a non-singular n × n matrix in ${\displaystyle A}$ ${\displaystyle b}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A=B+(A-B)}$.

So follows

${\displaystyle Ax=b}$

${\displaystyle Bx+(A-B)x=b}$

${\displaystyle \Rightarrow x=B^{-1}b-B^{-1}(A-B)x=(E-B^{-1}A)x+B^{-1}b}$,

where denotes the identity matrix . ${\displaystyle E}$

The system of linear equations is then equivalent to the fixed point problem with ${\displaystyle Ax=b}$ ${\displaystyle x=\varphi (x)}$

${\displaystyle \varphi (x)=(E-B^{-1}A)x+B^{-1}b}$.

The following iteration method is obtained for a given start vector for ${\displaystyle x_{0}}$ ${\displaystyle k=0,1,\ldots }$

${\displaystyle x_{k+1}=(E-B^{-1}A)x_{k}+B^{-1}b}$,

and the associated iteration matrix is: . ${\displaystyle E-B^{-1}A}$

convergence

From Banach's fixed point theorem and further considerations it follows that these fixed point methods converge for every start vector if and only if the spectral radius of the iteration matrix ${\displaystyle x_{0}}$

${\displaystyle \rho (E-B^{-1}A)=\max _{i}|\lambda _{i}(E-B^{-1}A)|<1}$.

${\displaystyle \rho (E-B^{-1}A)}$ should be as small as possible, as this determines the speed of convergence.

Special procedures

The following known methods for solving systems of linear equations are based on the above construction idea:

• Gauss-Seidel method or single -step method (ESV)
• Jacobi method or overall step method (GSV)

Remarks

Iteration methods of the form , k = 0, 1, ... are ${\displaystyle x_{k+1}=Mx_{k}+v}$

• linear , d. H. x _{k + 1} depends linearly only on x _k ,
• stationary , d. H. M and v are independent of the step number of the iteration,
• single stage , d. H. only the last and not further proximity vectors are used.

Nonlinear equations

The Newton method can be viewed as a fixed point iteration. In general, the convergence is ensured with the help of Banach's fixed point theorem , so the function under consideration must be a contraction , especially in the area under consideration .

literature

• Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists. 2nd Edition. Springer-Verlag, Berlin 2008, ISBN 978-3-540-76492-2 .

Individual evidence

1. ↑ Suitable transformations: zeros and fixed points. In: Montanuniversität Leoben . February 23, 2005, accessed August 27, 2019 .