Quadratic function

A quadratic function (also a completely rational function of the second degree ) is a function that has a polynomial of degree 2 as a function term , i.e. of the form
- With
is. The graph is the parabola with the equation . For is a linear function .
The functions of the form with (also ) are called special quadratic functions . The function with is called the square function .
Quadratic function and special quadratic function
The function with the assignment rule is called the square function . Your graph is a parabola that opens upwards and is symmetrical to the y-axis, the vertex of which lies at the origin of the coordinates , the normal parabola .
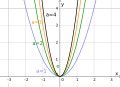
A function of the form with is called a special quadratic function . Your graph is a parabola symmetrical to the axis with a vertex at the origin. This arises from the normal parabola by stretching or compressing in the direction of the -axis and, if necessary, mirroring about the -axis:
- : The parabola is open upwards.
- : The parabola is open downwards.
- : The graph is compressed in the direction of the -axis, i.e. H. compressed in length, making it appear wider and flatter.
- : The graph is stretched in the direction of the -axis, i.e. H. elongated, making it appear narrower and steeper.
For : the graph is simply mirrored on the -axis compared to the normal parabola .
General quadratic function
The assignment rule for the general quadratic function is . The coefficients , and determine the range of values and the shape of the graph.
Parameters a
How the value of changes the shape of the graph is best seen by putting and . A normal parabola is then obtained that is stretched or compressed and, if necessary, mirrored about the axis .
- : The graph is open at the top.
- : The graph is open downwards.
- : The graph is compressed in the direction of the -axis, i.e. H. compressed in length, making it appear wider and flatter.
- : The graph is stretched in the direction of the -axis, i.e. H. elongated, making it appear narrower and steeper.
For : the graph is simply mirrored on the -axis compared to the normal parabola .
Parameters c
It applies . The parameter is therefore the value of the intersection of the parabola with the axis. A change in the parameter causes a shift in the direction. If you increase by one, the graph is shifted up by one unit. If you decrease by one, however, the graph is shifted down by one unit.
Parameters b
The parameter indicates the slope of the parabola at the point of intersection with the axis. In particular, you can see from the sign of whether the -axis is intersected with the falling or the rising branch of the parabola. From this, in turn, conclusions can be drawn about the number and possible position of zeros.
A change in the parameter causes a shift in both the - and - direction. If you increase by one, the graph is shifted by units to the left and down. If you decrease by one, however, the graph is shifted by units to the right and up.
Vertex
The vertex is decisive for the position of the parabola and represents either the absolute minimum (if is positive) or the absolute maximum (if is negative). The coordinates of the vertex can be read off directly if the function term is in the vertex form:
- .
The vertex then has the coordinates . The graph is axisymmetric to a line parallel to the -axis through .
There are several methods of determining the vertex or the vertex shape:
Determination of the vertex shape with a square extension
The vertex shape can be determined from the representation by adding a square .
Example: Determining the vertex shape of the quadratic function .
| The original functional equation | |
| The factor in front of has been excluded, with the constant term + 5 being excluded. | |
| A square addition is carried out too . | |
| The addition of a square makes it easy to extract a square from a part of the term using the binomial formulas . | |
| Now the brackets with the factor 2 have been removed again in order to simplify the term. | |
| The vertex can now be read in the final shape . |
Determine the vertex using the derivative
The differential calculus offers another possibility to calculate the vertex . Since the vertex is always a (local) extreme point (maximum or minimum), the zero of the first derivative of the function supplies the value of the vertex:
- ,
Inserting the value gives :
Example: Determining the vertex of the quadratic function .
| The original functional equation | |
| The 1st derivative of the function | |
| Determination of the zero of the 1st derivative by equating it with zero | |
| use in | |
| to calculate |
So the vertex has the coordinates .
Vertex calculation using known zeros
If the zeros of the quadratic function are known, the coordinates of the vertex can be calculated as follows:
- .
Intersection with the y-axis
Because of this , the intersection of the graph with the axis has the coordinates .
Zeroing a quadratic function
The zeros of a quadratic function are obtained by solving the equation , i.e. the quadratic equation
- .
These can be calculated using the abc formula:
If the expression under the root ( discriminant ) assumes a negative value, this means that no (real) zeros exist.
Zeros and linear factors
If and are the zeros of the quadratic function , the function equation can also be written as the product of its linear factors:
Intersection of parabola and straight line
be the functional equation of a parabola and that of a straight line. Approach: equating the functional equations quadratic equation. If now:
- The parabola and the straight line intersect at two points ( secant ).
- The parabola and the straight line touch at a point ( tangent ).
- The parabola and the straight line have no intersection ( passer-by ).
Intersection of two parabolas
be the functional equations of two parabolas. Approach: equating the functional equations quadratic equation. If now:
- The parabolas intersect in two points.
- The parabolas touch at one point.
- The parabolas have no intersection.
- is a linear equation The parabolas have an intersection.
Quadratic polynomial
Be any ring . Expressions of the form are called quadratic polynomials over
with and . Formally, these are elements of the polynomial ring of degree 2, they define mappings from to . In the case it is a question of quadratic functions in the above sense.
If is an algebraically closed field , every quadratic polynomial decays as the product of two linear factors.
More generally, quadratic polynomials in variables are expressions of the form
- ,
whereby not all should be zero. These polynomials define mappings from to . Their sets of zeros in are called quadrics , in this case also as conic sections .
literature
- Karin Hantschel, Lutz Schreiner, Michael Bornemann, Wiebke Salzmann: Knowledge - Practice - Testing: Mathematics 9th grade . Bibliographisches Institut, 2017, ISBN 9783411912315 , pp. 27–34
- Heinz Rapp: Mathematics for the technical college . Springer, 2015, ISBN 9783834809148 , pp. 156–170






































































![{\ displaystyle ax ^ {2} + bx + c \ in R [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/045b6862a605c90b9c28693870bd31d3be9aecb8)




![{\ displaystyle \ sum _ {i, j = 1} ^ {n} a_ {i, j} x_ {i} x_ {j} + \ sum _ {i = 1} ^ {n} b_ {i} x_ { i} + c \ in R [x_ {1}, \ ldots, x_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5d7568dc19b11f98a510d7b60c9f89407eb9e9)


