Quite rational function
A completely rational function or polynomial function is a function in mathematics that can be described as the sum of power functions with natural exponents . This means that such functions can only be described using the addition, subtraction and multiplication operations. Wholly rational functions belong to the rational functions and in turn contain the linear and quadratic functions as special cases .
This article deals mainly with the completely rational functions over the real numbers, which are common in school mathematics. Further information on possible generalizations of the concept can be found in the article Polynomial .
definition
A completely rational function is a real function that is expressed in the shape
can be written, where a natural number and real numbers are and applies. The number is called the degree of the function, the numbers are its coefficients . The coefficient is called the lead coefficient. The summand is called the absolute term, the summands and are sometimes referred to as the linear or quadratic term.
The representation of the completely rational function given here is its normal form . For example, a completely rational function can also be represented by means of linear factors or by means of the Horner schemes .
Examples
- The function with the term is a completely rational function of degree 3 with the coefficients and .
- With the function , the function term must first be rewritten into a sum by opening the brackets:
- so the degree is 4 and the coefficients are and .
- For an entirely rational function of degree with the coefficients , the function term can be written as .
Special cases
- There are constant functions for
- There are linear functions for (instead of writing for the slope here , and instead of writing for the -axis section ).
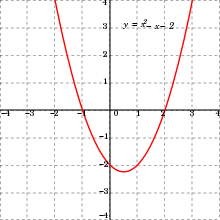
- For there are quadratic functions (instead of and one writes here , and ).
- There are cubic functions for .
- For sometimes called quartic functions .
- If only and all other coefficients are equal , then a power function with a natural exponent results .
Algebraic properties
The addition and multiplication of two completely rational functions result in completely rational functions. Thus the set of completely rational functions forms an algebra . For the degree of completely rational functions and the estimation or equality apply
and
- .
Denotes the degree of .
In addition, the concatenation of two completely rational functions is again a completely rational function, that is, a completely rational function is obtained again if a completely rational function is used for the function variable.
symmetry
- If all exponents are even numbers, then the graph of the function is axisymmetric to the y-axis. The function is then also called straight ; it applies .
- If all exponents are odd numbers, the graph of the function is point-symmetric to the origin. The function is then also called odd ; it applies .
- If both even and odd exponents occur, the graph does not have a simple symmetry; but it can still be symmetrical to other axes or points.
Examples:
- The graph of the function is symmetrical about the -axis (only even exponents: 6, 4 and 2).
- The graph of the function is symmetrical to the origin (only odd exponents: 7 and 1).
- The graph of the function has no simple symmetry (odd and even exponents: 3 and 0), but is point-symmetric about its inflection point .
- The graph of every rational function of the second degree is axisymmetric to the vertical axis through its vertex .
- The graph of every fully rational function of the third degree is point-symmetric to its inflection point .
Boundary behavior
In general, the behavior for is determined by the summands with the highest exponent, the behavior for by the summands with the lowest exponents.
growth
Wholly rational functions can be understood as linear combinations of powers . Therefore they grow more slowly (for sufficiently large values) than any exponential function whose base is greater than 1, regardless of the coefficients.
Behavior for very large and very small x values
All completely rational functions diverge for . The exact behavior depends on whether the degree n is even or odd and the sign of the leading coefficient ; the graph behaves exactly like the graph of a power function with the term . In the following, the resulting set of values is also given for the case that the definition set is.
| n straight | n odd | |
|---|---|---|
| The graph runs from top left to top right, so: for is bounded downwards (by the absolute minimum of the function)
|
The graph runs from bottom left to top right, so: for and for |
|
| The graph runs from bottom left to bottom right, so: for is bounded upwards (by the absolute maximum of the function)
|
The graph runs from top left to bottom right, so: for and for |
Behavior for x values close to zero
All completely rational functions are finite. More precisely, the following applies: the graph intersects the -axis , the slope at this point is given by. The tangent at the point of intersection with the axis therefore always has the equation
example
The graph of the function runs like the graph of the function , i.e. from top left to bottom right (degrees odd, leading coefficient ). The following applies to the function values: for and for . For , on the other hand, it runs like the graph of , i.e. it intersects the -axis and has the slope there .
zeropoint
Linear factorization
If the function term of a completely rational function is given as a product of linear factors (some of which can also occur multiple times) and possibly a completely rational function g without zeros, i.e.
so are the zeros. The natural numbers are called the multiples of the zeros .
Example: The function
has the triple zero , the single zero and the double / double zero ; the factors and , on the other hand, cannot become zero for none , so do not provide any further zeros.
The linear factorization of a completely rational function can be determined, for example, with the help of the polynomial division . From the fundamental theorem of algebra it follows that every completely rational function over the complex numbers can be broken down into a product of linear factors. If the function only has real coefficients, it follows that with every complex zero, the conjugate complex number is also a zero. This means that every completely rational function over the real numbers can be represented uniquely (except for the sequence) as a product of linear and quadratic terms.
The multiplicity of zeros is also directly related to the derivatives of the function: is a -fold zero of if and only if and .
Course of the graph at the zeros
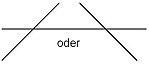
- The graph intersects the axis at every zero point of odd multiplicity . The function values change their sign there. In the case of simple zeros, the axis is cut at an angle greater than 0 °. For every zero point of odd multiplicity greater than or equal to three, the slope at the zero point is 0; the function graph has a terrace point .
- The graph touches the -axis at every zero point of even multiple . The function values do not change their sign there. At every such zero the function graph has an extreme point .
graphic illustration:
| simple zero | three, five, 2k + 1 zero position | double, quadruple, 2k zero position |
|---|---|---|
 |
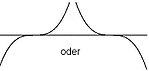 |

|
If you also consider the behavior for , the following graph results for the above example :
Methods for calculating the zeros
To find zeros, the algebraic equation has to be solved. There are (among others) the following methods for this:
- Linear equations can be solved directly using equivalent transformations . The zeros are then always easy.
- For quadratic equations , there are various methods of solution; see the corresponding article. The following applies: if there are two different solutions, both are simple; if there is only one solution, it is double.
- Often times, the function term can be factored directly by factoring out powers of or by using the binomial formulas . The multiplicities can then be read off directly in the linear factor decomposition.
- If only and are not equal to zero, i.e. for functions with terms of the form , the zeros result simply with the help of the -th root . These zeros are then always easy.
- The substitution method helps with some equations, especially biquadratic ones . The following applies: If you have a (positive!) Single or double solution of the corresponding quadratic equation after the substitution, this results in two single or double zeros of the function itself.
- If a zero can be found by trial and error, the associated linear factor can be divided out with the help of a polynomial division and an algebraic equation of a lower degree is obtained. The multiplicities of the zeros are obtained here simply by counting how often a zero comes out in the calculation. The following sentences are helpful for finding a zero by trying it out:
- If all coefficients are integer , then all integer zeros are dividers of the absolute term (note: there may also be non-integer zeros). If the coefficients are all rational numbers , you can always achieve by multiplying by the main denominator that all the coefficients are integers.
- If all the coefficients have the same sign, the zeros cannot be positive.
- The Cardan formulas can be used for fully rational third-degree functions ; for fully rational functions of the fourth degree there are similar formulas for quartic equations .
- Zero points can also be determined approximately, for example with the Newton method .
number
With the help of the polynomial division one can show that a completely rational function of degree can have zeros at most (multiples counted).
If one also considers the behavior of the graph for , the behavior at the zeros ( change of sign ) and the continuity , it also follows: if the degree is even or odd, then the total number of zeros (including multiples) is even or odd . In particular, it follows: Every completely rational function of odd degree has at least one zero.
There are also other, more advanced rules for the number of zeros such as Descartes' sign rule and the Sturm chain .
Differentiation and integrability
Derivative function
Completely rational functions can be differentiated over completely continuously . Functions that can be differentiated completely or completely are called whole functions . The derivative function can be determined using the factor , sum and power rule . This gives for the function with the rule
the derivative function
- .
Integrability and antiderivative
Every completely rational function can be integrated on a compact interval . In addition, every completely rational function has an antiderivative . This can be specified explicitly with the usual integral rules. The following applies:
where is any constant.
Examples
For the function with the term
the derivative function results with the term
In this case one obtains for the antiderivatives
Extreme points
(see also the article Kurvendiskussion the section on extreme points )
To determine the extreme points, the points with a horizontal tangent, i.e. the zeros of the first derivative, must first be calculated. The first derivation is again a completely rational function, but of degree ; The same methods can therefore be used as for calculating the zero.
General rules
- If the function itself has a zero of even multiplicity, then its graph has an extreme point there (see above under zeros).
- If the sign of the first derivative changes from - to + at one point, there is a minimal point there; if it changes from + to -, there is a maximum place; if the sign does not change, there is no extreme point there (but a terrace point ).
- If the second derivative is positive or negative at a zero of the first derivative, the first derivative there changes its sign from - to + (minimum digit) or from + to - (maximum digit). If the second derivative is equal to zero, there can still be an extreme point at this point, but there can also be a terrace point there. Means other than the second derivative are then necessary to differentiate.
- If a zero of the first derivative has an odd multiplicity, the function itself has an extreme there; if, on the other hand, it has a multiplicity, the function has a terrace point at this point .
number
From the theorem about the number of zeros of a completely rational function it follows that a completely rational function of degree can have at most extreme points.
If one also considers the behavior of the graph for and the behavior at the zeros (change of sign), it also follows: if the degree is even or odd, then the total number of extreme positions is odd or even.
In particular, it follows: Every completely rational function of an even degree has an absolute minimum or maximum (depending on whether the leading coefficient is positive or negative).
Turning points
(see also the section on turning points in the article curve discussion )
To determine the turning points, the zeros of the second derivative, the so-called flat points, must first be calculated. The second derivation is again a completely rational function, but of degree ; The same methods can therefore be used as for calculating the zero.
General rules
- If the function itself has a zero point of odd multiplicity greater than or equal to three, then its graph has a terrace point there , i.e. also a turning point (see above for zeros).
- If the sign of the second derivative changes at one point, there is a turning point there.
- If the third derivative is not equal to zero at a zero of the second derivative, the sign of the second derivative changes there (turning point). If the third derivative is zero, there can still be a turning point at this point, but it does not have to. Means other than the third derivative are then necessary to differentiate.
- If a zero of the second derivative has an even multiplicity, the function itself has no turning point there; on the other hand, if the zero of the first derivative has an odd multiplicity, the function itself has a turning point there. If the first derivative is also zero at this point, the graph of the function has a terrace point there .
- The following applies particularly to functions of the third degree:
- The high and low point (if any) are always symmetrical to the point of inflection (this follows because the graphs of functions of the third degree are always symmetrical to their point of inflection, see above).
- If the function itself has three (not necessarily different) real zeros, the turning point results as its mean value, weighted with the multiples. (If, on the other hand, there is only one real zero, the complex zeros must also be taken into account when calculating the mean value .)
number
From the theorem about the number of zeros of a completely rational function it follows that a completely rational function of degree can have at most turning points.
If one also considers the behavior of the graph for and the behavior at the zeros (change of sign), it also follows: if the degree is even or odd, the total number of turning points is even or odd.
In particular, it follows: Every completely rational function of an odd degree greater than or equal to three has at least one turning point.
Establishing functional terms
Often a problem has to be solved as follows: There are some points and possibly additional conditions (such as gradients in these points), and a completely rational function is sought whose graph runs through these points and possibly fulfills the additional conditions. In order to find this completely rational function, one first sets up the function term in the most general possible form (the degree is either given directly or must be determined from the other given information), forms any necessary derivatives of the function in this general form and then sets the given conditions. This leads to a linear system of equations for the coefficients of the function; instead of , etc. these are usually referred to here with etc. By solving this system of equations, one then obtains the term of the function sought.
Example: We are looking for a completely rational function of the lowest possible degree, whose graph is symmetrical to the axis and has a slope of 2 at the point of inflection .
- Since the graph should be symmetrical about the -axis, the degree must be even and the function term can only contain even exponents.
- Since there is supposed to be a turning point, the degree cannot be 2 (a function of the second degree has no turning point); so the lowest possible grade is 4.
- The functional term in its most general form is:
- Since we are talking about a turning point, two derivatives are required:
- The graph runs through the point , so the following applies ( insert - and coordinate in )
- The graph has slope 2 there, so the following applies ( insert coordinate and slope in )
- The point is a turning point, so the following applies ( must be 0 at the turning point )
- Overall, the linear system of equations results
- Solving this system of equations gives . So the term of the function we are looking for is:
Application examples
- Many of the curves that occur in nature and technology can be described relatively well using completely rational functions, for example terrain formations, ski jumps or the deflection of beams.
- Quite rational functions often appear in geometric applications. Examples:
- If you cut out squares of the side length at the corners of a rectangular cardboard (length , width ) and then fold the cardboard into a box that is open at the top, the volume of the box is the same .
- If you stack balls (e.g. oranges in the supermarket) to form a three-sided pyramid, with balls lying along a base edge, then the pyramid contains balls as a whole .
- Tax tariffs are often described by completely rational functions ( PDF ).
- In economic applications, the revenue function is often an entirely rational function of the third degree.
- Since completely rational functions are particularly simple, more complicated functions are often approximated by completely rational ones (cf. Taylor series and Weierstrass's approximation theorem ). This approach is used in particular in analysis and numerics . Alternatively, there are also situations in which a finite number of function values are specified and a function is sought that runs through these points. These can polynomial interpolation can be used. In addition, a finite set of function values can also be interpolated piece-wise using completely rational functions. This procedure is called spline interpolation . If you want to evaluate a completely rational function at one point numerically efficiently (optimized for computers), the Horner scheme can be used.
literature
- H. Schneider, G. Stein: Mathematics 11 and Mathematics 12: Analysis for non-technical training courses in the technical college.
- R. Schöwe, J. Knapp, R. Borgmann: Analysis: Commercial-economic direction for technical college.
Web links
Individual evidence
- ↑ Rational function . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .