Root (math)
In mathematics , extracting a root or square root is the determination of the unknown in the power
Here is a natural number (usually greater than 1) and an element from a body (often a nonnegative real number ). The result of the root extraction is called root or radical (from Latin radix "root"). Square root is a reverse of exponentiation . In case it is called square in of cube roots . Roots are noted with the help of the root symbol, in the example the root or the radical is .
Definition, ways of speaking and writing
Let it be a natural number. If a nonnegative real number, then the equation has
exactly one nonnegative real solution. This is called the -th root of . One writes for it:
This is called
- as a root , radical or radix ,
- as a root sign ,
- as the root exponent ,
- as a radicand .
Occasionally one also looks at the case , in which case simply holds.
Square and cube roots
Usually the second root is called the square root or just the root and the root exponent is omitted:
The root with the root exponent 3 (third root) is also known as the cube root .
Example:
(Say: the third root of 8 is 2 or the cube root of 8 is 2 )
Mathematical basics
The following description of the square root function as a right unambiguous root function refers to the arranged field of the real numbers , so to a certain extent to school mathematics . A more general root term, including the one described here, is covered in the article Adjunction (Algebra) .
Connection with potencies
The square root with the root exponent and the exponentiation with the exponent cancel each other out. According to the above definition of the root, the following applies to all real numbers and to all natural numbers :
The square root with the root exponent works like the exponent power . According to the calculation rules for powers:
Therefore the square root with the root exponent n can also be interpreted as exponentiation with the exponent 1 / n :
Uniqueness of roots from positive numbers
Although the question mentioned at the beginning has two solutions with different signs for even-numbered root exponents and positive radicands, the notation with the root sign basically stands for the positive solution. For example, the equation has two solutions and . However, the term has the value +2 and not the value −2. In general, therefore, applies to even-numbered root exponents
Roots of negative numbers
The treatment of roots from negative numbers is not uniform. For example
and is the only real number whose cube is. In general, negative numbers result for odd powers of negative numbers.
With regard to the odd roots of negative numbers, the following positions are represented:
- Roots from negative numbers are generally not defined. For example, it is therefore undefined. The solution to the equation is written as .
- Roots from negative numbers are defined if the root exponent is an odd number (3, 5, 7, ...). The following generally applies to odd numbers
- .
- This definition is incompatible with some properties of the roots that apply to positive radicands. For example is
- This definition does not work with the equation either , since the (natural) logarithm of negative numbers is not defined ( so it must not be negative).
Roots to even exponents of negative numbers cannot be real numbers because even powers of real numbers are never negative. There is no real number , so you can't find a root that is in the real numbers. The need for roots from negative numbers led to the introduction of complex numbers ; However, there are certain difficulties with the definition of one of the roots in the area of complex numbers with the term root, see below .
Irrational roots from whole numbers
If a nonnegative integer and a positive integer, it is either an integer or an irrational number. One proves this by applying the uniqueness of the prime factorization :
Is , so is , therefore an integer. Otherwise there is a prime factorization that is unambiguous except for the order of the factors with pairwise different prime numbers and positive whole exponents . Are all for by , so is divisible , so an integer.
Now it still has to be shown: If there is at least one with so that is not divisible by , then it is irrational. The proof for the irrationality occurs indirectly, i.e. by refuting the opposite assumption as in the proof of the irrationality of the root of 2 in Euclid , which is essentially the special case of this proof.
Suppose would be rational. Then you could write the number as a fraction of two natural numbers and :
- .
By raising the equation to the power of
and it follows
- .
The prime factor occurs in or in each case- times as often as in or , at least in a multiplicity that can be divided by, whereby, of course, 0 occurrences are also permitted. In , according to the assumptions, it occurs in the not divisible multiplicity . So it does not appear on the left side of this equation in a multiplicity that can be divided by divisors, but it does on the right, and we get a contradiction to the uniqueness of the prime factorization. Hence is irrational.
The Root Laws
The calculation rules for roots result from those for powers .
The following calculation laws apply to positive numbers and and :
- Product rule:
- Quotient rule:
- "Nesting rule" or iteration rule:
- Definition of a fractional exponent:
- Definition for negative exponent:
- With the same radical, the following applies:
With negative numbers and , these arithmetic laws may only be used if and are odd numbers. In the case of complex numbers, they are to be avoided entirely, or equality only applies if the secondary values are appropriately selected. In other words: if any roots (e.g. only main values) are selected on the left-hand side , there are suitable secondary values for the right-hand side that satisfy the equality - left and right-hand sides differ by a unit root .
Limit values
The following limit values apply :
- For
- This follows from the inequality that can be shown with the aid of the binomial theorem .
- , where is any fixed natural number.
- ,
- as can be seen from the exponential representation of .
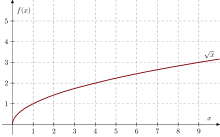
Root functions
Functions of form
- or more general
are called root functions. They are power functions , it holds .
calculation
Roots can be determined by drawing roots in writing . This procedure is similar to written division and is based on the binomial formulas . It was still taught in high school until the 1960s, but is of little practical importance today.
Relation to other functions
Like any power, higher roots of positive numbers can be expressed in terms of an exponential function and a logarithm :
Numerical calculation
Several methods can be used to approximate a root. These include the interval halving procedure .
Another approximation method for calculating is obtained by using the Newton method to set a zero of the function
- approximates:
- Choose a starting value (as good as possible)
- Iterate by the rule
For you just get the Heron procedure .
Example of an approximation for using the iteration method above:
The iteration rule is with and
- .
With the start value you get:
| Starting value: | 2.000000000000 |
| Step 1: | 1,500000000000 |
| Step 2: | 1.296296296296 |
| Step 3: | 1.260932224741 |
| Step 4: | 1.259921860565 |
| Step 5: | 1.259921049895 |
| Step 6: | 1.259921049894 |
Method of the "mathematician"
As arithmetic artists do, a root can also be determined by estimating and applying elementary number theory , provided that it is known that the root is a natural number . This can be shown particularly well using the example of the third root. To do this, you need to know two things, namely the magnitude of the cube numbers, and the last digit of the number:
|
|
Examples:
- The third root of 103,823:
The number is between 64,000 and 125,000, so the tens of the third root must be 4. The last digit of the number is a 3, so the third root of 103,823 is estimated 47. - The third root of 12,167:
The number is between 8,000 and 27,000, so the tens of the third root must be 2. The last digit of the number is a 7, so the third root of 12,167 is estimated 23.
The whole thing only works if you can assume that the given number is the third power of a natural number.
The mathematicians' tasks are of course about much higher powers of multi-digit numbers - for example the calculation of the 25th root of 880,794,982,218,444,893,023,439,794,626,120,190,780,624,990,275,329,063,400,179,824,681,489,784,873,773. 249 (answer: 1729) and more extreme tasks.
Complex number roots
The complex numbers are defined by the adjunct of the solution (root) of the equation to the real numbers . If one understands the complex numbers as a plane in which the real numbers as a distinctive straight line divides the plane into two half planes and the positive numbers are on the right, then the number is placed in the upper and in the lower half plane. Simultaneously with this orientation, the function for increasing real things revolves around the zero point in the mathematically positive sense (i.e. counterclockwise), so that is. With this stipulation, inherently ambiguous roots in the complex can be set to unambiguous real and imaginary parts ( main values). Nevertheless, the care mentioned there must be observed when applying the root laws .
The solutions of the equation are called the -th roots of a complex number
- .
If shown in the exponential form, the -th roots of are exactly the complex numbers
The special case is called the -th equation of a circle , the solutions as -th roots of unity . The designation "circle division equation" is explained when one considers its solutions in the Gaussian plane: the -th roots of unit divide the circle with the radius and the origin as the center into equal parts, they form the corner points of a regular -gon inscribed in the circle .
Unlike with real numbers, it is not so easy to mark one of the roots as the root; there you choose the only non-negative root. However, it is a ( holomorphic ) th root function for complex numbers, which are not non-positive real numbers, via the main branch of the complex logarithm define:
The so distinguished root is also called the main value, the others as secondary values.
The logarithm can also be continued (discontinuously) on the negative real axis, but then with the root function defined in this way, for example, and not .
literature
- Hans Kreul, Harald Ziebarth: Mathematics made easy . 7th edition. Verlag Harri Deutsch, 2009, ISBN 978-3-8171-1836-6 . Chapter on the calculation of roots with explanations, examples and exercises (PDF; 535 kB).
Web links
Individual evidence
- ↑ The other inversion is taking the logarithm .
- ↑ a b T. Arens, F. Hettlich et al .: Mathematics. 2008, pp. 46-47.
- ↑ The root exponent for square root corresponds to the logarithm for logarithmizing and the exponent for exponentiation. The radicand corresponds to the number (logarithmand) when taking the logarithm and the result of the exponentiation
- ^ Lothar Kusch: Mathematics . Volume 1: Arithmetic. Algebra, series theory, nomography . W. Girardet, Essen 1975, ISBN 3-7736-2755-6 , p. 162 f.
- ↑ For the difficulties with the right uniqueness s. a. the § roots of complex numbers .
- ↑ DIN 1302 : 1999 General mathematical symbols and terms
- ↑ EN ISO 80000-2: 2020 quantities and units - Part 2: Mathematics
- ^ T. Arens, F. Hettlich et al .: Mathematics . 2008, p. 122.
-
↑ This can be avoided by highlighting that root among all those whose argument modulo delivers the absolutely smallest remainder. If two values are equal, then the one in the right (positive real part) and the one in the upper half-plane (positive imaginary part) must be selected. This rule is fully compatible with the rules for real radicands given above. Some examples:
-
Although and and is with the absolute remains of the argument
because the mean root has a positive real part with the same absolute remainder .
In addition, with this definition the laws of roots for many root exponents are retained, even with complex radicands, as long as the sums of the remainders modulo of the argument values for the roots selected in this way remain absolutely below .








![{\ displaystyle x: = {\ sqrt [{n}] {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/640515457bfa1a33bcb3ceebbedfcba5c8728d58)


![{\ displaystyle x = {\ sqrt [{n \,}] {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5b247ec7cb0b4dc530599781caf66474e9b4b37)
![{\ sqrt [{n \,}] {a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/713d5ed1e8c82b01e898a9b9788aa678aabe5ab5)


![{\ sqrt [{1 \,}] {a}} = a](https://wikimedia.org/api/rest_v1/media/math/render/svg/395d1ccce97a71bc1bdd70dac58d27397e455865)
![{\ sqrt {a}} = {\ sqrt [{2}] {a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/703568c12856d81ba503e45df79ef89b2eac426a)
![{\ sqrt [{3}] {8}} = 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f378331b0d609846c021c1a0bbff0a4fc1755c3)


![\ left ({\ sqrt [{n}] {a}} \ right) ^ {n} = a](https://wikimedia.org/api/rest_v1/media/math/render/svg/64cb04ba3b309b574960aaf2b7141e4faae06216)


![{\ sqrt [{n}] {a}} = a ^ {\ frac {1} {n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2211e22214f87e6a2303d3d4c2465a3229984bde)
![{\ sqrt [{}] {}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2728884d0378cc133178d711fe6fef12aad386f6)



![{\ sqrt [{2}] {4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b6caa44c96c5446c370b7e361bc7995a5f88e6b)
![{\ sqrt [{2n}] {x ^ {2n}}} = | x | \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd28bc64b4878d053459208c9b779b449d1f450f)



![{\ sqrt [{3}] {- 8}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1042604e3bf8b89ddd4771fcc19dbb36b05ce423)

![x = - {\ sqrt [{3}] {8}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e80c22580c362b386e1a421324d0b7a2f01c06)

![{\ sqrt [{2n + 1}] {- a}} = - {\ sqrt [{2n + 1}] {a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/853a51339773f257d26c74c4ab194d3d14afe0c3)
![-2 = {\ sqrt [{3}] {- 8}} \ neq {\ sqrt [{6}] {(- 8) ^ {2}}} = {\ sqrt [{6}] {64}} = + 2.](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef94c9d7cc0583ab90a2ccd29f9d0fbcd44e8a29)
![{\ displaystyle {\ sqrt [{k}] {a}} = a ^ {\ frac {1} {k}} = \ exp \ left ({\ tfrac {1} {k}} \ ln (a) \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/216d5c54f7f67bb0ebca1cfcf89fdcba53d0e91c)

![x = {\ sqrt [{2}] {- 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1812089401a487eead8d3598b99a8faef4f797e)

![{\ sqrt [{k}] {n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81bef6d66e5171e992486e360c88405f74418934)

![{\ displaystyle {\ sqrt [{k}] {n}} = n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0bd2f81f0e524e982629ec402cd925677ee6f0)





![{\ displaystyle {\ sqrt [{k}] {n}} = p_ {1} ^ {e_ {1} / k} \ dotsm p_ {r} ^ {e_ {r} / k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/791988f073b0073488922c56bfc7936279cbce00)



![{\ displaystyle {\ sqrt [{k}] {n}} = {\ frac {a} {b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4268bd657206acd28fbb5f63a5750b6ee29cf4f)






![{\ sqrt [{n}] {a}} \ cdot {\ sqrt [{n}] {b}} = {\ sqrt [{n}] {a \ cdot b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb1cdc44e892d181f2e52332608a940e0d9f9a6b)
![{\ frac {\ sqrt [{n}] {a}} {\ sqrt [{n}] {b}}} = {\ sqrt [{n}] {\ frac {a} {b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a051c5fb0f6593e2d1e6a84d3ab614ffbab3eb2)
![{\ sqrt [{m}] {{\ sqrt [{n}] {a}}}} = {\ sqrt [{m \ cdot n}] {a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1ef8ace9d360ced62f31f7d66eca161594dfc83)
![{\ displaystyle a ^ {\ frac {k} {n}} = {\ sqrt [{n}] {a ^ {k}}} = \ left ({\ sqrt [{n}] {a}} \ right ) ^ {k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/454a14abc9cf67996458174bdece47ad99abf16e)

![{\ displaystyle {\ sqrt [{m}] {a}} \ cdot {\ sqrt [{n}] {a}} = a ^ {{\ frac {1} {m}} + {\ frac {1} {n}}} = {\ sqrt [{mn}] {a ^ {m + n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59645055e4042edf582c276a2456fe9af63bb6a3)

![\ lim _ {n \ rightarrow \ infty} {\ sqrt [{n}] {a}} = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/16410a3cae5fccc56d11e2ffbd30531952f0dd23)

![\ lim _ {n \ rightarrow \ infty} {\ sqrt [{n}] {n}} = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d1dd63871920301086721f8d139653b5c276c71)
![n <\ left (1 + {\ sqrt [{2}] {\ tfrac {2} {n}}} \ right) ^ {n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/899811ee94f8bbe73cd9e6eec5b97aa6bb8344ca)
![\ lim _ {n \ to \ infty} {\ sqrt [{n}] {n ^ {k}}} = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb5737609390c2a26534847bb035f57313b69633)

![{\ sqrt [{n}] {n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61402e0a053d2f40af8ee61ff361d232500e92d6)
![f \ colon \ mathbb {R} _ {0} ^ {+} \ to \ mathbb {R} _ {0} ^ {+}, x \ mapsto {\ sqrt [{n}] {x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac3e293c7e03dcc3cc38c88700e4137f03ca57e1)
![x \ mapsto {\ sqrt [{n}] {x ^ {m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c02b2d66b50710298e8786139c80d90b584e54a)
![{\ sqrt [{n}] {x ^ {m}}} = x ^ {\ frac {m} {n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d91b3c9d16a74ea1b7bc7f51573f8204a6f7e76)
![{\ sqrt [{n}] {x}} = x ^ {1 / n} = \ exp \ left ({\ frac {\ ln (x)} {n}} \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2bb2ed4d8062b36de5395ac4819fd894258a512)
![{\ sqrt [{n}] {x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)



![{\ sqrt [{3}] {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)







![{\ sqrt [{3}] {z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27f2f0f796cf622e8d14e33cb7754a127742271b)

















![z_ {k} = {\ sqrt [{n}] {| a |}} \ cdot \ exp \ left ({\ frac {\ mathrm {i} \ varphi} {n}} + k \ cdot {\ frac { 2 \ pi \ mathrm {i}} {n}} \ right) \ quad (k = 0.1, \ dots, n-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/b95dd909ff351d3aa92313e41486fd67f04e0563)



![{\ displaystyle {\ sqrt [{3}] {- 8}} = 2 \, \ exp {{\ bigl (} \ mathrm {i} \, {\ tfrac {\ pi} {3}} {\ bigr) }} = 1+ \ mathrm {i} {\ sqrt {3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c024ae6bb6da45ff8b68ae9c4dcf8656ab816b)

![{\ displaystyle \ arg ({\ sqrt [{n}] {z}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aad00ed6b6396b405ccb8c0ae9d0bf07ed2a6ca)

![{\ displaystyle {\ sqrt [{2}] {- 1}} = + \ mathrm {i} \ qquad \ qquad {\ sqrt [{3}] {- 1}} = - 1 \ qquad \ qquad {\ sqrt [{4}] {- 1}} = {\ frac {{\ sqrt {2}} + \ mathrm {i} {\ sqrt {2}}} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8352e42391f319afbee1862bdb9c339ead15be)
![{\ displaystyle {\ sqrt [{3}] {- \ mathrm {i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cfda4342e51da96981bd3cdc80e1d4559491980)




![{\ displaystyle {\ sqrt [{3}] {- \ mathrm {i}}} = {\ frac {{\ sqrt {3}} - \ mathrm {i}} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc79ed43b076651878837adf72d373beefcfec38)








