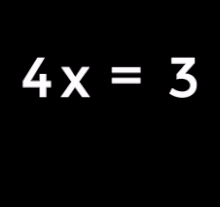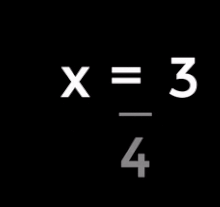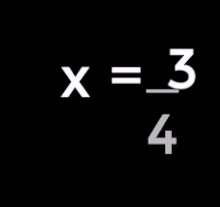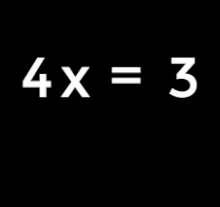Equivalent conversion

In mathematics , equivalence conversion ( Latin aequus = equal; valere = to be) denotes a conversion of an equation or inequality that leaves the truth value unchanged ( logical equivalence ). The transformed logical statement is therefore true for the same variable assignment as the original statement. Equivalence transformations are the primary method for solving equations and inequalities .

In order for a transformation to be an equivalent transformation, the following must apply:

• There is a reverse transformation (inverse operation) which can be used to undo the transformation.
• The solution set of the equation or inequality remains unchanged.

Equivalence conversions are usually carried out in the space of real numbers , since there the number space is neither limited upwards nor downwards.

With an equivalence conversion, both sides of the equation or inequality are always converted. If only one of the sides is rewritten, it is a term rewrite instead .

Equivalence transformations of equations

The following transformations are permitted for equations:

• Addition of a term
• Subtract a term
• Multiplication with a term other than 0
• Division by a term other than 0
• Application of a bijective function

Addition and subtraction

An equivalent conversion is, for example, the addition or subtraction of a term on both sides. Subtract from the equation

${\displaystyle x+5=7}$

the number 5 (by subtracting the number on both sides) gives the equation

${\displaystyle (x+5)-5=(7)-5}$

and finally by simplifying the two sides

${\displaystyle x=2}$.

Multiplication and division

Multiplication by 4 or division by 4

The multiplication or division of a term on both sides of the equation, as long as it is not equal to 0, is also an equivalence conversion.

It should be noted that multiplication by zero or division by zero is often hidden; for example, the multiplication by is not an equivalent conversion, since this multiplier can be zero in the case of this . However, one can by case analysis , to ensure that a multiplication or division with zero is not taking place: cases in which a multiplier or divisor is zero, are to be examined separately; otherwise, the transformed statements are only equivalent to one another under a corresponding additional requirement (i.e. not generally). ${\displaystyle x-1}$ ${\displaystyle x=1}$

Division by 0 in an alleged equivalence transformation is a well-known example of a mathematical fallacy .

Application of a bijective function

The transformation through addition, subtraction, multiplication and division can be generalized, for example by considering the operation as a function . ${\displaystyle {}+3}$ ${\displaystyle t\mapsto t+3}$

Such a function must be unique both in the forward and in the reverse direction. Such functions are called bijective .

Counterexample: squaring

In the real number space, squaring is not an equivalence transformation because squaring has no clear inverse function. For example, the equation has one real solution, while the squared equation has two real solutions (namely and ). ${\displaystyle x=2}$ ${\displaystyle x^{2}=4}$ ${\displaystyle +2}$ ${\displaystyle -2}$

However, if you restrict the permitted range of numbers for , you can also make squaring an equivalent conversion. ${\displaystyle x}$

For example , assuming that the equations and are equivalent. ${\displaystyle x\leq 0}$ ${\displaystyle x^{2}=4}$ ${\displaystyle x=-2}$

On the other hand , assuming that the equations and are equivalent. ${\displaystyle x\geq 0}$ ${\displaystyle x^{2}=4}$ ${\displaystyle x=+2}$

Equivalence transformations of inequalities

In the case of inequalities, the law of inversion must be observed, according to which the order relation changes direction when multiplied by or divided by a negative number. For example, multiply the inequality

${\displaystyle x>y\!}$

with −5, one obtains the equivalent inequality

${\displaystyle -5x<-5y\!}$.

Division by −5 again yields the original inequality.

In general, the application of a strictly monotonic function to both sides of an inequality is an equivalence conversion; with strictly monotonically increasing functions the direction of the order relation is retained; with strictly monotonically decreasing functions, the order relation changes direction. The above example of multiplication by −5 on both sides corresponds to the application of the strictly monotonically decreasing function . ${\displaystyle t\mapsto -5t}$

If you multiply an inequality by a number whose sign is not known, a case distinction is necessary. For example, one would like the inequality

${\displaystyle {\frac {x+3}{x-2}}<2}$

like to multiply by, but it is not known whether or is true (the case must be excluded, since the left side of the inequality would then not even be defined). If true, therefore results in the case against it . Thus the given inequality is overall equivalent to ${\displaystyle x-2}$ ${\displaystyle x>2}$ ${\displaystyle x<2}$ ${\displaystyle x=2}$ ${\displaystyle x>2}$ ${\displaystyle x+3<2x-4}$ ${\displaystyle x<2}$ ${\displaystyle x+3>2x-4}$

${\displaystyle (x>2{\text{ und }}x+3<2x-4){\text{ oder }}(x<2{\text{ und }}x+3>2x-4)}$

this in turn too

${\displaystyle (x>2{\text{ und }}7<x){\text{ oder }}(x<2{\text{ und }}7>x).}$

so overall

${\displaystyle x<2{\text{ oder }}x>7.}$

Instead of dealing with the logical combinations together with regard to equivalence, as is the case here, it is customary to deal with the cases one after the other and separately and to summarize them at the end.

notation

Equivalence transformations are usually indicated with an equivalence arrow ⇔ (Unicode U + 21D4). Applied to the above example:

${\displaystyle x+5=7\Leftrightarrow x=2\!}$

Representation of the transformation operation: In school mathematics in particular , equivalence transformations are often shown with a vertical line after the (in) equation which operation should be applied next on both sides of the (in) equation. The above examples are then written in the form

${\displaystyle x+5=7\;\;\;\;\;\;\;\;|-5}$

${\displaystyle x=2\;}$

or.

${\displaystyle x>y\;\;\;\;\;\;\;\;\;\;\;\;|\cdot (-5)}$

${\displaystyle -5x<-5y\;}$.

Web links

Wikibooks: Math for Non-Freaks: Equations: Transformations  - Learning and Teaching Materials

• Equivalence Transformation - Introduction for Students (Video)