Solving inequalities

When solving inequalities using real numbers , one tries to simplify a confusing inequality to such an extent that simple statements of the form x> 5 can be formed that can be understood directly or that can be illustrated using the number line . In principle, the same basic rules apply here as for solving equations . However, the asymmetry of the comparison signs also requires special attention to the signs of the transformations. ${\displaystyle <,\leq ,\geq ,>}$

Basic rules

Similar to solving equations, inequalities are solved using equivalent conversions. This means that a number of actions are allowed - provided they are carried out the same on both sides. In the following, only the less than or equal sign is considered; analogous statements apply, however, if the less than or equal sign is replaced by one of the other symbols or . ${\displaystyle \leq }$ ${\displaystyle \leq }$ ${\displaystyle >,<}$ ${\displaystyle \geq }$

Without limitation, addition and subtraction of the same expression on either side are equivalent conversions . So it holds for two real-valued terms and any ${\displaystyle T_{1}(x),\ T_{2}(x)}$ ${\displaystyle a\in \mathbb {R} }$

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)+a\leq T_{2}(x)+a}$ such as

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)-a\leq T_{2}(x)-a}$.

When multiplying by the same expression and when dividing by the same expression, attention must be paid to the sign: For two real-valued terms and with applies ${\displaystyle T_{1}(x),\ T_{2}(x)}$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle a>0}$

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)\cdot a\leq T_{2}(x)\cdot a}$ such as

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)\div a\leq T_{2}(x)\div a}$.

For , however, the order relation is reversed: ${\displaystyle a<0}$

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)\cdot a\geq T_{2}(x)\cdot a}$ such as

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow T_{1}(x)\div a\geq T_{2}(x)\div a}$.

Obviously the case is not an equivalent transformation. ${\displaystyle a=0}$

Generally applies to a bijective strictly monotonically increasing function ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow f\left(T_{1}(x)\right)\leq f\left(T_{2}(x)\right)}$,

for a bijective strictly monotonically decreasing function , however, the order relation is reversed: ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$

${\displaystyle T_{1}(x)\leq T_{2}(x)\Leftrightarrow f\left(T_{1}(x)\right)\geq f\left(T_{2}(x)\right)}$.

The cases of addition, subtraction, multiplication and division described above are special cases of this general rule; for example, multiplication with corresponds to the application of the function that increases for bijective and strictly monotonically, for bijective and strictly monotonically decreasing, for neither bijective nor strictly monotonous is. ${\displaystyle a}$ ${\displaystyle x\mapsto a\cdot x}$ ${\displaystyle a>0}$ ${\displaystyle a<0}$ ${\displaystyle a=0}$

Often one would like to use functions that are strictly monotonic not on the whole , but only on a subset . This is possible if it is ensured that the terms lie in this subset. For example, for a bijective function that increases strictly monotonically ${\displaystyle \mathbb {R} }$ ${\displaystyle T_{1}(x),\ T_{2}(x)}$ ${\displaystyle f\colon \mathbb {R} ^{+}\to \mathbb {R} ^{+}}$

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow 0<f\left(T_{1}(x)\right)\leq f\left(T_{2}(x)\right)}$,

for a bijective strictly monotonically decreasing function ${\displaystyle f\colon \mathbb {R} ^{+}\to \mathbb {R} ^{+}}$

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow f\left(T_{1}(x)\right)\geq f\left(T_{2}(x)\right)>0}$.

In this case it must either be shown that it must actually always apply, or a case distinction must be made by first examining the case and then treating the cases and separately. ${\displaystyle 0<T_{1}(x)}$ ${\displaystyle 0<T_{1}(x)\leq T_{2}(x)}$ ${\displaystyle T_{1}(x)\leq 0\leq T_{2}(x)}$ ${\displaystyle T_{1}(x)\leq T_{2}(x)<0}$

The most important special case is raising both sides to the power of the same exponent :

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow 0<\left(T_{1}(x)\right)^{a}\leq \left(T_{2}(x)\right)^{a}}$for , ${\displaystyle a>0}$

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow \left(T_{1}(x)\right)^{a}\geq \left(T_{2}(x)\right)^{a}>0}$for . ${\displaystyle a<0}$

${\displaystyle a={\frac {1}{2}}}$corresponds to pulling the square root :

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow 0<{\sqrt {T_{1}(x)}}\leq {\sqrt {T_{2}(x)}}}$,

${\displaystyle a=-1}$forming the reciprocal value :

${\displaystyle 0<T_{1}(x)\leq T_{2}(x)\Leftrightarrow {\frac {1}{T_{1}(x)}}\geq {\frac {1}{T_{2}(x)}}>0}$.

Types of inequalities

Linear inequalities

Single linear inequalities can be solved by addition, subtraction and multiplication with constants similar to linear equations . An important approach to systems of linear inequalities in several variables is provided by pivot methods and, more generally, methods of linear optimization .

Quadratic inequalities

In the case of quadratic inequalities, the solution domain is usually divided into three sections, which result from the quadratic equation corresponding to the inequality . These are the sections blue - red - blue in the illustration shown under Graphic Processes . Either all values ​​marked in blue or all values ​​marked in red on the x-axis are now possible solutions.

Solution with a square extension

One method of solving this is essentially based on square completion . As an example, the inequality x² - 0.5 · x - 0.5> 0 should be solved, which is shown in the figure below.

x² - 0.5 x x - 0.5	> 0	+ 0.5
x² - 0.5 x x	> 0.5	+ (0.5: 2) ²	Add the square of half the amount of the linear term.
x² - 0.5 x + 0.25²	> 0.5625		Exclude.
(x - 0.25) 2	> 0.75²		Take root.

Here you can't just “shorten the square”. But since the roots can be drawn on both sides. It should be noted that . So we have to distinguish between two cases: ${\displaystyle 0{,}75^{2}>0}$ ${\displaystyle {\sqrt {(x-0{,}25)^{2}}}=|x-0{,}25|}$

Case 1: . Then the inequality has to be solved, so it holds , whereby in this case the prerequisite is also fulfilled. ${\displaystyle x\geq 0{,}25}$ ${\displaystyle x-0{,}25>0{,}75}$ ${\displaystyle x>1}$ ${\displaystyle x\geq 0{,}25}$

Case 2: . Then the inequality has to be solved, so the following applies , whereby the prerequisite is also fulfilled in this case . ${\displaystyle x<0{,}25}$ ${\displaystyle 0{,}25-x>0{,}75}$ ${\displaystyle -0{,}5>x}$ ${\displaystyle x<0{,}25}$

These two statements have no area of ​​overlap. Then, as one can easily confirm by trial and error, all numbers that are either less than −0.5 or greater than +1 are solutions to the inequality.
If, on the other hand, one had to solve the inequality x² - 0.5 · x - 0.5 <0 , the solution statements would be x> −0.5 and x <+1 . All numbers between −0.5 and +1 fulfill both conditions and would therefore be solutions.

Forming on product

Solving by means of quadratic completion requires several case distinctions, which can become confusing. Another solution method for quadratic inequalities is the inequality directly to a product of nature , , or to bring. As an example, the inequality shown in the figure below should also be solved. ${\displaystyle \left(x-a\right)\left(x-b\right)>0}$ ${\displaystyle \left(x-a\right)\left(x-b\right)<0}$ ${\displaystyle \left(x-a\right)\left(x-b\right)\geq 0}$ ${\displaystyle \left(x-a\right)\left(x-b\right)\leq 0}$ ${\displaystyle x^{2}-{\frac {1}{2}}x-{\frac {1}{2}}>0}$

The quadratic equation corresponding to the inequality

${\displaystyle x^{2}-{\frac {1}{2}}x-{\frac {1}{2}}=0}$

has the solutions and , so it applies ${\displaystyle x_{1}=-{\frac {1}{2}}}$ ${\displaystyle x_{2}=1\!}$

${\displaystyle x^{2}-{\frac {1}{2}}x-{\frac {1}{2}}=\left(x+{\frac {1}{2}}\right)\left(x-1\right)}$

and the inequality is equivalent to

${\displaystyle \left(x+{\frac {1}{2}}\right)\left(x-1\right)>0}$.

If one now looks at the sections of the number line divided by the two solutions of the quadratic equation, one finds that both factors are negative and the product is therefore positive and both factors are positive and the product is therefore also positive. This is the blue area in the picture. In the section in between , and , the product is therefore not positive. This is the area marked in red. ${\displaystyle x<-{\tfrac {1}{2}}}$ ${\displaystyle x>1}$ ${\displaystyle -{\tfrac {1}{2}}\leq x\leq 1}$ ${\displaystyle (x+{\tfrac {1}{2}})\geq 0}$ ${\displaystyle (x-1)\leq 0}$

If the quadratic equation belonging to the inequality has no real solution , so then the relation holds for all x ; the inequality either has no solution at all or is fulfilled for all real numbers. ${\displaystyle x^{2}+px+q=0}$ ${\displaystyle q>{\tfrac {p^{2}}{4}}}$ ${\displaystyle x^{2}+px+q=(x-{\tfrac {p}{2}})^{2}+(q-{\tfrac {p^{2}}{4}})>0}$

Higher order inequalities

In the case of inequalities of order 3 and above, usually only the conversion to an inequality for a product is practicable, for example by converting an inequality of order 3 to the form for real or for a pair of complex zeros. This factorization is possible according to the fundamental theorem of algebra for inequalities of any high order. The analytical calculation of the zeros is not always possible, so that a numerical method such as bisection must usually be used. A graphical solution can be helpful when looking for suitable starting values. ${\displaystyle \left(x-a\right)\left(x-b\right)\left(x-c\right)>0}$ ${\displaystyle \left(x-a\right)\left(x^{2}+bx+c\right)>0}$

Fractional inequalities

Transformation on inequalities between polynomials

There are only new aspects for solving fraction inequalities if the required quantity x also appears in at least one of the denominators. By multiplying the equation on both sides by the denominators and then multiplying it out, the fraction inequality is converted into an inequality of two polynomials .

When multiplying by the denominators, you must first determine for which values ​​of x you will assume a negative value, since the multiplication then reverses the comparison sign. If there is a range of x in which both denominators are negative, the comparison sign is reversed twice, which cancels each other out. This preliminary investigation is known as a case distinction .

Take the inequality as an example

${\displaystyle {\frac {x-1{,}6}{x+0{,}2}}<{\frac {0{,}2-x}{x+0{,}6}}}$

to be viewed as. As can be easily seen, a denominator becomes zero whenever either x = −0.2 or x = −0.6 . For these values ​​of x , the inequality is not defined ( division by zero ). If, on the other hand, x is less than −0.6 ( x <−0.6 ), both denominators are negative; for x> −0.2 both are positive. Then there is no reversal of the comparison sign and multiplying the inequality by the denominators results in:

(x − 1.6) (x + 0.6) <(0.2 − x) (x + 0.2) .

Otherwise (x is between −0.6 and −0.2) only the left denominator becomes negative. In this case, the multiplication and the following equivalence conversions result :

(x − 1.6) (x + 0.6)	> (0.2 − x) (x + 0.2)		multiply!
x² − 1x − 0.96	> 0.04 - x²		+ x² −0.04
2x² − 1x − 1	> 0		÷ 2
x² − 0.5x − 0.5	> 0

This is the quadratic inequality that was solved earlier. Your solution would be the blue area of the figure. However, since this calculation only applies to the range between −0.6 and −0.2 (see above), only values ​​between −0.6 and −0.5 remain from the blue area.

Finally we have to consider the cases x <−0.6 and x> −0.2 , for which the comparison sign is not reversed. Solution of the generated quadratic inequality would then be the red area of the figure. However, since this calculation does not apply to the range between −0.6 and −0.2, the only solution area for the inequality is the values ​​between −0.2 and +1.

Conclusion: The inequality is fulfilled for −0.6 <x <−0.5 and for −0.2 <x <+1 .

Forming on product

Another method for solving fraction inequalities is also to transform the fraction inequality into a statement about the sign of products or quotients. The advantage of this procedure is that fewer case distinctions have to be made.

The inequality

${\displaystyle {\frac {x-1{,}6}{x+0{,}2}}<{\frac {0{,}2-x}{x+0{,}6}}}$

to be viewed as. Instead of multiplying by the denominator, all terms are put on one page; this conversion only requires subtraction and therefore no case differentiation according to the sign:

${\displaystyle {\frac {x-1{,}6}{x+0{,}2}}-{\frac {0{,}2-x}{x+0{,}6}}<0.}$

Then the fractions are brought to a common denominator, whereby the denominator should not be multiplied because it will be needed later in the product representation:

${\displaystyle {\frac {\left(x-1{,}6\right)\left(x+0{,}6\right)-\left(0{,}2-x\right)\left(x+0{,}2\right)}{\left(x+0{,}2\right)\left(x+0{,}6\right)}}<0.}$

Then the counter is multiplied and combined

${\displaystyle {\frac {2x^{2}-1{,}0x-1}{\left(x+0{,}2\right)\left(x+0{,}6\right)}}<0.}$

Next, according to the Fundamental Theorem of Algebra , the numerator is factored into linear and irreducible quadratic terms; In the concrete example, the quadratic equation already solved above is to be solved, so one obtains

${\displaystyle {\frac {2\left(x+0{,}5\right)\left(x-1\right)}{\left(x+0{,}2\right)\left(x+0{,}6\right)}}<0.}$

To determine the amount of solution, it is sufficient to only consider the signs of the respective factors, since these signs together determine the sign of the product. For this purpose, the number line is divided into individual sections, each limited by the zeros of the factors; in each of these sections the signs of the factors are constant.

${\displaystyle x}$	Signs of the factors	Sign of the product	<0
${\displaystyle x<-0{,}6}$	${\displaystyle {\frac {(-)\cdot (-)}{(-)\cdot (-)}}}$	${\displaystyle (+)}$	No
${\displaystyle x=-0{,}6}$	${\displaystyle {\frac {(-)\cdot (-)}{(-)\cdot 0}}}$	undefined	No
${\displaystyle -0{,}6<x<-0{,}5}$	${\displaystyle {\frac {(-)\cdot (-)}{(-)\cdot (+)}}}$	${\displaystyle (-)}$	Yes
${\displaystyle x=-0{,}5}$	${\displaystyle {\frac {0\cdot (-)}{(-)\cdot (+)}}}$	${\displaystyle 0}$	No
${\displaystyle -0{,}5<x<-0{,}2}$	${\displaystyle {\frac {(+)\cdot (-)}{(-)\cdot (+)}}}$	${\displaystyle (+)}$	No
${\displaystyle x=-0{,}2}$	${\displaystyle {\frac {(+)\cdot (-)}{0\cdot (+)}}}$	undefined	No
${\displaystyle -0{,}2<x<1}$	${\displaystyle {\frac {(+)\cdot (-)}{(+)\cdot (+)}}}$	${\displaystyle (-)}$	Yes
${\displaystyle x=1}$	${\displaystyle {\frac {(+)\cdot 0}{(+)\cdot (+)}}}$	${\displaystyle 0}$	No
${\displaystyle x>1}$	${\displaystyle {\frac {(+)\cdot (+)}{(+)\cdot (+)}}}$	${\displaystyle (+)}$	No

Conclusion: The inequality is fulfilled for −0.6 <x <−0.5 and for −0.2 <x <+1 .

The systematic use and presentation of this procedure leads to the sign table .

Amount inequalities

Amount inequalities are inequalities that contain at least one amount . Just like absolute equations, they can be solved by differentiating cases , in exceptional cases (!) (See below) also by squaring. In the following, a numerical example of the solution to a simple absolute value inequality is presented:

Let the inequality be given

${\displaystyle |x+1|<5}$.

The cases are obtained with the help of a case distinction

1. ${\displaystyle x+1\geq 0\wedge x+1<5\Rightarrow x\geq -1\wedge x<4}$ and
2. ${\displaystyle x+1<0\wedge -(x+1)<5\Rightarrow x<-1\wedge x>-6}$.

The solution set of the inequality as a whole is thus the union of the partial solution sets that are directly adjacent in this case, i.e. H. . ${\displaystyle L}$ ${\displaystyle L=\left]-6;-1\right[\cup \left[-1;4\right[=\left]-6;4\right[}$

The above inequality could exceptionally (!) Be solved by squaring, which in this case is about

${\displaystyle {\begin{aligned}(x+1)^{2}<&5^{2}\\\Leftrightarrow x^{2}+2x+1<&25\\\Leftrightarrow x^{2}+2x-24<&0\\\Rightarrow x_{1/2}\lessgtr &-{\frac {2}{2}}\pm {\sqrt {{\frac {2^{2}}{2^{2}}}+24}}\\\Leftrightarrow x_{1/2}\lessgtr &-1\pm 5\,\end{aligned}}}$

would lead to the same result, but would have the disadvantage that squaring the inequality would make the inequality longer, and above all the sign of the right side of the inequality would be lost and thus, for example, the two inequalities and the same solution set would have. ${\displaystyle |x+1|>5}$ ${\displaystyle |x+1|>-5}$

The following example of a somewhat more difficult absolute value inequality illustrates the case in which both partial solution sets can not be combined to form a connected interval:

Let the inequality be given

${\displaystyle x+3\leq |4x-2|}$.

With the help of the case distinction one now obtains the cases

1. ${\displaystyle 4x-2\geq 0\wedge x+3\leq 4x-2\Rightarrow x\geq {\tfrac {1}{2}}\wedge x\geq {\tfrac {5}{3}}}$ and
2. ${\displaystyle 4x-2<0\wedge x+3\leq -(4x-2)\Rightarrow x<{\tfrac {1}{2}}\wedge x<{\tfrac {-1}{5}}}$.

The solution set of the inequality as a whole is here again the union of the two partial solution sets, which in this case are not adjoining each other. H. . ${\displaystyle L}$ ${\displaystyle L=\left]-\infty ;{\tfrac {-1}{5}}\right[\cup \left[{\tfrac {5}{3}};+\infty \right[}$

Graphic process

graphical solution of x²> 0.5x + 0.5 (blue) or x² <0.5x + 0.5 (red)

Graphical methods can give clues about the number and position of the solutions within the framework of the drawing accuracy.

If the inequality is in a form corresponding to the normal form of equations, the left-hand side can be viewed as a function, the graph of which is to be drawn with sufficient accuracy according to a table of values . The areas to the left or right of the zeros (i.e. intersection points with the x-axis ) then graphically represent the solution sets.
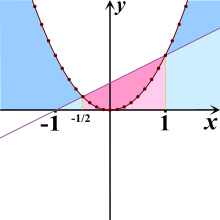
Otherwise, the functions corresponding to the right and left side of the inequality are to be plotted together in an axbox. The x-values ​​of the intersections indicate the boundaries of the solution areas. Bring quadratic inequalities of the straight line resulting from the right side to the intersection. This is shown as an example on the right for the inequality x² <0.5x + 0.5 (red area) or x²> 0.5x + 0.5 (blue area).

See also

• Solving equations
• Pivot procedure

literature

• E. Cramer, J. Neslehova: Preliminary course in mathematics: workbook for the beginning of studies in economics and social sciences. Springer Berlin Heidelberg New York, 2006, p. 302, ISBN 3-540-26186-9 .

Individual evidence

1. ^ Franz Embacher; Absolute equations and the method of case distinctions ; University of Vienna 2014 , accessed June 19, 2016.