Pivot procedure

This article covers pivot methods in mathematical optimization. For pivot selection using the Gaussian elimination method, see there.

Pivot methods (also basic exchange methods ) are algorithms of mathematical optimization , in particular of linear optimization . For a given system of linear equations in nonnegative variables (essentially the same as a system of linear inequalities ), the best possible alternative solution (a so-called optimal solution ) is searched for, and the system of equations is converted step by step without changing the solution set. Important pivot processes are the simplex process and the criss-cross process.

Pivot methods play an analogous and similarly important role for the treatment of linear inequalities as the Gaussian elimination method for the solution of linear systems of equations in unlimited variables. The main area of ​​application of the pivot method is linear optimization: they are among the most widely used solution methods in business research , economics , and goods transport , and they are also increasingly used in many other areas such as civil engineering (structural optimization ), statistics (regression analysis) and game theory used. Tasks with tens of thousands of variables and inequalities are the order of the day.

Pivot approach

Problem

A pivot method always starts from a special kind of linear system of equations in which all variables, except perhaps one, should assume non-negative values. Each system of linear inequalities or equations, and also any linear optimization problem , namely can be in the following (English dictionary called) book form bring:

${\displaystyle {\begin{matrix}z&=&f&+&~~~~~d_{1}\,x_{1}&+&\cdots &+&~~~~~d_{n}\,x_{n}\\[3pt]x_{n+1}&=&b_{n+1}&+&G_{n+1,1}\,x_{1}&+&\cdots &+&G_{n+1,n}\,x_{n}\\\vdots &&\vdots &&\vdots &&&&\vdots \\x_{n+m}&=&b_{n+m}&+&G_{n+m,1}\,x_{1}&+&\cdots &+&G_{n+m,n}\,x_{n}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~z\,,\quad x_{1}\geq 0,\;\ldots ,\;x_{n+m}\geq 0\end{matrix}}}$

Here are real (mostly rational in practice ) numbers. The above notation is intended to indicate that a solution is sought in the unknowns that satisfies the corresponding equations and inequalities and thereby selects the so-called target variable as large as possible. ${\displaystyle f,\;d_{j},\;b_{i},\;G_{i,j}}$ ${\displaystyle x_{1},\;\ldots ,\;x_{n+m},\;z}$ ${\displaystyle z}$

comment

When the task is transformed into the above form, the inequalities of the system do not diminish: they remain present in at least the same number and now appear as nonnegative variables. A common linear inequality such as

${\displaystyle 3x_{1}~+~4x_{2}~-~x_{3}~\leq ~5x_{1}~+~8}$

is transformed into

${\displaystyle x_{4}~=~8~+~2x_{1}~-~4x_{2}~+~x_{3}}$

with . ${\displaystyle x_{4}\geq 0}$

With the help of the index sets

${\displaystyle D=\{1,\ldots ,n\},\quad B=\{n+1,\ldots ,n+m\}}$

this task can also be expressed in compact form as follows:

${\displaystyle {\begin{matrix}&&z&=&f&+&\sum _{j\in D}\,d_{j}\,x_{j}\\[6pt]\forall ~i\in B&&x_{i}&=&b_{i}&+&\sum _{j\in D}\,G_{i,j}\,x_{j}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~z\,,\quad \forall ~k\in D\cup B\quad x_{k}\geq 0\end{matrix}}}$

In each step of a pivot method, as above, a subset of the variables is highlighted as independent , while the remaining variables, called base variables, are expressed as linear-affine functions of the independent variables. In successive steps, one of the variables changes from independent to basic variable and a second changes in the opposite direction; such pairs of variables are called pivots .

Optimum conditions

If the following two optimum conditions are met in the linear system of equations established above

• ${\displaystyle b_{i}\geq 0}$   for all      (admissibility) and ${\displaystyle i\in B}$
• ${\displaystyle d_{j}\leq 0}$   for everyone      (target restriction), ${\displaystyle j\in D}$

then one can get a solution to the above problem by setting the independent variables to the values . On the one hand, the values ​​of the exposed variables are then nonnegative, as required. On the other hand, other possible solutions may only contain independent variables with likewise non-negative values, so that the inequality applies to each of these solutions . ${\displaystyle x_{1}=0,\ldots ,x_{n}=0}$ ${\displaystyle x_{n+1}=b_{n+1},\ldots ,x_{n+m}=b_{n+m}}$ ${\displaystyle z\leq f}$

In the following example system,

${\displaystyle {\begin{matrix}z&=&~~~0&-~3x_{1}&+~~\mathbf {x_{2}} \\[2pt]x_{3}&=&~~~3&-~~x_{1}&-~~x_{2}\\[2pt]x_{4}&=&~~~8&+~2x_{1}&-~4x_{2}\\[2pt]x_{5}&=&-~\mathbf {1} &+~3x_{1}&+~~x_{2}\,,\end{matrix}}}$

the optimum conditions are violated in two places, there and is. First, the test solution would contain the negative value , and second, its target variable value could possibly be increased in solutions with . ${\displaystyle b_{5}=-1<0}$ ${\displaystyle d_{2}=+1>0}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle x_{5}=-1}$ ${\displaystyle z=-3x_{1}+x_{2}}$ ${\displaystyle x_{2}>0}$

Exchange of the basic variables

If the optimum conditions are not met, which is usually the case, the above system of linear equations can also be expressed differently by selecting another, equally large subset of the unknowns instead of and exposing them . It is     a change of the unknown. Based on the following distribution of the variables, ${\displaystyle \{x_{n+1},\ldots ,x_{n+m}\}}$ ${\displaystyle n+m}$ ${\displaystyle \pi (1),\ldots ,\pi (n+m)}$

${\displaystyle D(\pi )=\{\pi (1),\ldots ,\pi (n)\},\quad B(\pi )=\{\pi (n+1),\ldots ,\pi (n+m)\},}$

into new independent variables with and new base variables with , the system of equations is now converted to ${\displaystyle x_{j}}$ ${\displaystyle j\in D(\pi )}$ ${\displaystyle x_{i}}$ ${\displaystyle i\in B(\pi )}$

${\displaystyle {\begin{matrix}&&z&=&f^{\pi }&+&\sum _{j\in D(\pi )}\,d_{j}^{\pi }\,x_{j}\\[6pt]\forall ~i\in B(\pi )&&x_{i}&=&b_{i}^{\pi }&+&\sum _{j\in D(\pi )}\,G_{i,j}^{\pi }\,x_{j}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~z\,,\quad \forall ~k\in D\cup B\quad x_{k}\geq 0\,,\end{matrix}}}$

Please note that entries are only defined with and for index pairs . The entries of the equation system converted in this way can now be checked again for the optimum conditions, ${\displaystyle G_{i,j}^{\pi }}$ ${\displaystyle i\in B(\pi )}$ ${\displaystyle j\in D(\pi )}$

• ${\displaystyle b_{i}^{\pi }\geq 0}$   for all      (admissibility) and ${\displaystyle i\in B(\pi )}$
• ${\displaystyle d_{j}^{\pi }\leq 0}$   for everyone      (target restriction), ${\displaystyle j\in D(\pi )}$

which in turn may lead to a solution to the problem.

A standard result of linear optimization says that for every solvable problem there is a set of basic variables that lead to a solution. If the optimum conditions are met, the basic variables form a so-called optimum basis of the system.

Pivots and pivot elements

Each non-vanishing system of equations above, the pivot system , is called a pivot element and allows the independent variable to be exposed instead of the base variable in order to continue searching for a solution. This is the procedure of a general pivot procedure, whereby not any pivot elements are selected, but only allowed (admissible) pivots that must meet the following: ${\displaystyle G_{r,s}^{\pi }\neq 0}$ ${\displaystyle x_{s}}$ ${\displaystyle x_{r}}$ ${\displaystyle (x_{r},\,x_{s})}$

• Either and    (admissibility pivot) apply simultaneously , ${\displaystyle b_{r}^{\pi }<0}$ ${\displaystyle G_{r,s}^{\pi }>0}$
• or it applies at the same time and    (target progress pivot). ${\displaystyle d_{s}^{\pi }>0}$ ${\displaystyle G_{r,s}^{\pi }<0}$

In the example system above,

${\displaystyle {\begin{matrix}z&=&~~~0&-~3x_{1}&+~~~\mathbf {x_{2}} \\[2pt]x_{3}&=&~~~3&-~~x_{1}&-~~~{\underline {\mathbf {x_{2}} }}\\[2pt]x_{4}&=&~~~8&+~2x_{1}&-~{\underline {\mathbf {4x_{2}} }}\\[2pt]x_{5}&=&-~\mathbf {1} &+~{\underline {\mathbf {3x_{1}} }}&+~~~{\underline {\mathbf {x_{2}} }}\,,\end{matrix}}}$

Pivoting with pivot and pivoting with pivot are allowed due to the violation of optimality . Because of the violation of optimality , pivot elements with pivot and pivot elements with pivot are also allowed. ${\displaystyle b_{5}<0}$ ${\displaystyle G_{5,1}=+3>0}$ ${\displaystyle (x_{5},\,x_{1}),}$ ${\displaystyle G_{5,2}=+1>0}$ ${\displaystyle (x_{5},\,x_{2})}$ ${\displaystyle d_{2}>0}$ ${\displaystyle G_{3,2}=-1<0}$ ${\displaystyle (x_{3},\,x_{2})}$ ${\displaystyle G_{4,2}=-4<0}$ ${\displaystyle (x_{4},\,x_{2})}$

The restriction to allowed pivots prevents the same pivot from being selected twice in a row. The rules according to which one of these permitted pivot elements is selected in each step depend on the respective procedure; A minimum requirement is, of course, that the process continues after a finite number of steps, which is not the case with an unsuitable selection of permitted pivots . Fukuda & Terlaky proved in 1999 that for every solvable task and for every starting point there is a sequence of maximally allowed pivots that leads to an optimal basis. Unfortunately, their proof does not provide a procedure to find these pivots in every optimization step. ${\displaystyle n+m}$

As can be seen from the definition, optimal bases do not have allowed pivots; in such a case , the procedure can not be continued. On the other hand, as can be easily shown in the above section of arguments based on that a non-optimal basis without allowing Pivots always belongs to a task that no solution has ; either because the system of equations and inequalities has no solution at all (impermissible problem), or because solutions of any size can be found (unlimited problem). ${\displaystyle z}$

Examples

A direct implementation

In order to avoid rounding errors, we will work with fractions in the following and choose a common denominator for all entries. In order to find a common denominator for the overall system in every step, we do n't have to examine the entries additionally. If the starting system is an integer (which can usually be achieved by expansion), the following rule applies:

• The numerator of the chosen pivot element is a common denominator for the following system.

If the entries of the following system are multiplied by this common denominator, whole-number values ​​are obtained. When the subsequent system is set up, the common denominator of the predecessor system becomes obsolete, which is why all entries in the subsequent system can be shortened without checking using this obsolete denominator.

A table with the entries of a pivot system is often called a tableau . The following diagram shows how the entries of the pivot systems change from one step to the next:

${\displaystyle {\begin{matrix}\delta \,x_{i}&\!=\!&(~~\alpha )&\!\!\!x_{j}&\!+\!&(~~\sigma )&\!\!\!x_{s}\\[6pt]\delta \,x_{r}&\!=\!&(~~\zeta )&\!\!\!x_{j}&\!+\!&(~~p)&\!\!\!x_{s}\end{matrix}}}$

${\displaystyle {x_{r}\leftrightarrow x_{s}}}$

${\displaystyle {\begin{matrix}p\,x_{i}&\!=\!&(\textstyle {\frac {\alpha p\,-\,\zeta \sigma }{\delta }})&\!\!\!x_{j}&\!+\!\!&(~\sigma )&\!\!\!x_{r}\\[6pt]p\,x_{s}&\!=\!&(~-\zeta ~)&\!\!\!x_{j}&\!+\!\!&(~\delta )&\!\!\!x_{r}\\\end{matrix}}}$

The symbol stands for the common denominator of the equation system, the symbol for the numerator of the pivot element , for another entry in the pivot line , for another entry in the pivot column , and for any entry apart from the pivot line and pivot column. Entries in the target contribution line ( ) and the base value column ( ) are converted according to the same rules. ${\displaystyle \delta \,}$ ${\displaystyle p\,}$ ${\displaystyle \zeta \,}$ ${\displaystyle \sigma \,}$ ${\displaystyle \alpha \,}$ ${\displaystyle x_{i}\!=\!z\,}$ ${\displaystyle x_{j}\!=\!1\,}$

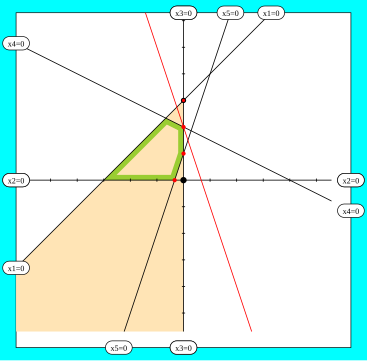
The pictures for the steps in the following examples all show the same system of equations in different orthogonal coordinates ; where:

• The area outlined in green is the permissible range in which all variables have nonnegative values.
• Coordinate axes correspond to the equations of independent variables; other straight lines describe exposed variables. ${\displaystyle x_{k}=0}$
• Intersections of allowed pivot points are marked in red; the intersection with a black border shows the selected pivot.
• The yellow area becomes the non-negative quadrant in the next step .

A sure-fire pivot selection rule

For now we will choose an example without a target variable, that is, with . In such a case, none of the variables are maximized; only arbitrary (non-negative) values ​​are searched for for the unknowns which satisfy a given system of equations. In each step we want to choose the allowed pivot according to the following rule: ${\displaystyle z=0+0\,x_{1}+0\,x_{2}}$ ${\displaystyle x_{1}\geq 0,\ldots ,x_{n+m}\geq 0}$ ${\displaystyle (x_{r},\,x_{s})}$

1. Choose , ${\displaystyle r=\min\{i\in B(\pi )~|~b_{i}^{\pi }<0\}}$
2. then choose . ${\displaystyle s=\min\{j\in D(\pi )~|~G_{r,j}^{\pi }>0\}}$

This (not particularly efficient) selection rule coincides with the Smallest Index Pivot Selection given below ; it can be proven that this selection leads to an optimal basis for every solvable task . ${\displaystyle z=0}$ ${\displaystyle z=0}$

We are now looking for values ​​for the unknowns that make up the system of equations ${\displaystyle x_{1}\geq 0,\ldots ,x_{5}\geq 0}$

${\displaystyle {\begin{matrix}x_{3}&=&(&-~\mathbf {2} &-~7x_{1}&+~{\underline {\mathbf {2x_{2}} }}&)~/~1\\[2pt]x_{4}&=&(&-~4&-~5x_{1}&+~2x_{2}&)~/~1\\[2pt]x_{5}&=&(&~~~9&+~2x_{1}&-~3x_{2}&)~/~1\end{matrix}}}$

fulfill. The allowed pivots in the above system of equations are and ; Due to the above selection rule, we expose the independent variable instead of the basic variable : ${\displaystyle (x_{3},\,x_{2})}$ ${\displaystyle (x_{4},\,x_{2})}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{3}}$

Base 0 to base 1 (scalable and animated by Firefox when clicking twice and holding down)

We now get the following converted system of equations:

${\displaystyle {\begin{matrix}x_{2}&=&(&~~~2&+~~7x_{1}&+~~~~x_{3}&)~/~2\\[2pt]x_{4}&=&(&-~\mathbf {4} &+~~{\underline {\mathbf {4x_{1}} }}&+~~~2x_{3}&)~/~2\\[2pt]x_{5}&=&(&~~12&-~17x_{1}&-~~~3x_{3}&)~/~2\end{matrix}}}$

In the new system the allowed pivots are and ; this time we lay bare instead of : ${\displaystyle (x_{4},\,x_{1})}$ ${\displaystyle (x_{4},\,x_{3})}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{4}}$

Base 1 to base 2

We now get the following system:

${\displaystyle {\begin{matrix}x_{2}&=&(&~~18&+~~7x_{4}&-~~5x_{3}&)~/~4\\[2pt]x_{1}&=&(&~~~4&+~~2x_{4}&-~~2x_{3}&)~/~4\\[2pt]x_{5}&=&(&-\mathbf {10} &-~17x_{4}&+~{\underline {\mathbf {11x_{3}} }}&)~/~4\end{matrix}}}$

The only pivot allowed here is ; therefore we can only expose instead of : ${\displaystyle (x_{5},\,x_{3})}$ ${\displaystyle x_{3}}$ ${\displaystyle x_{5}}$

Base 2 to base 3

Well we get

${\displaystyle {\begin{matrix}x_{2}&=&(&~~37&-~~2x_{4}&-~~~5x_{5}&)~/~11\\[2pt]x_{1}&=&(&~~~6&-~~3x_{4}&-~~~2x_{5}&)~/~11\\[2pt]x_{3}&=&(&~~10&+~17x_{4}&+~~~4x_{5}&)~/~11\end{matrix}}}$

This system fulfills the optimality conditions and accordingly has no allowed pivots. By setting all independent variables to zero, we get the following solution:

${\displaystyle x_{1}=6/11=0.55,x_{2}=37/11=3.36,x_{3}=10/11=0.91,x_{4}=0,x_{5}=0\,.}$

Circulatory pivot selection rules

The following is an example of improper pivot selection; If the pivot selection is unsuitable, a pivot procedure can get into an infinite cycle (an endless loop ). Again, as suggested in the following rule, we might succumb to the temptation to select the pivot row only from the "most violated" constraints, and understand "most violated" as those with the most negative constants: ${\displaystyle \,z=0+0\,x_{1}+0\,x_{2}\,.}$

1. Choose , ${\displaystyle r=\min {\big \{}i\in B(\pi )~|~~b_{i}^{\pi }\!=\!\min\{b_{k}^{\pi }\,|\,k\in B(\pi ),~b_{k}^{\pi }\!<\!0\}~{\big \}}}$
2. then choose . ${\displaystyle s=\min\{j\in D(\pi )~|~G_{r,j}^{\pi }>0\}}$

To show that something like this can go wrong, let's start with the system:

${\displaystyle {\begin{matrix}x_{3}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{1}} }}&+~~x_{2}&)~/~2\\[2pt]x_{4}&=&(&~~~6&-~7x_{1}&-~3x_{2}&)~/~2\\[2pt]x_{5}&=&(&~~~0&-~3x_{1}&-~~x_{2}&)~/~2\\[2pt]x_{6}&=&(&~~~4&+~7x_{1}&+~~x_{2}&)~/~2\end{matrix}}}$

We choose here and expose instead . This gives us the system: ${\displaystyle \,x_{3}\,}$ ${\displaystyle \,x_{1}\,}$

${\displaystyle {\begin{matrix}x_{1}&=&(&~~~2&+~2x_{3}&-~~x_{2}&)~/~1\\[2pt]x_{4}&=&(&-~\mathbf {4} &-~7x_{3}&+~{\underline {\mathbf {2x_{2}} }}&)~/~1\\[2pt]x_{5}&=&(&-~~3&-~3x_{3}&+~~x_{2}&)~/~1\\[2pt]x_{6}&=&(&~~~9&+~7x_{3}&-~3x_{2}&)~/~1\end{matrix}}}$

We choose basic variables , expose them in their place , and get: ${\displaystyle \,x_{4}\,}$ ${\displaystyle \,x_{2}\,}$

${\displaystyle {\begin{matrix}x_{1}&=&(&~~~0&-~3x_{3}&-~~x_{4}&)~/~2\\[2pt]x_{2}&=&(&~~~4&+~7x_{3}&+~~x_{4}&)~/~2\\[2pt]x_{5}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{3}} }}&+~~x_{4}&)~/~2\\[2pt]x_{6}&=&(&~~~6&-~7x_{3}&-~3x_{4}&)~/~2\end{matrix}}}$

The entries in this system of equations are the same as in the start system, which is why the entries in the following systems are repeated every two steps if the pivot sequence is similar. After selecting the basic variables to expose in their place , we get: ${\displaystyle \,x_{5}\,}$ ${\displaystyle \,x_{3}\,}$

${\displaystyle {\begin{matrix}x_{1}&=&(&-~~3&-~3x_{5}&+~~x_{4}&)~/~1\\[2pt]x_{2}&=&(&~~~9&+~7x_{5}&-~3x_{4}&)~/~1\\[2pt]x_{3}&=&(&~~~2&+~2x_{5}&-~~x_{4}&)~/~1\\[2pt]x_{6}&=&(&-~\mathbf {4} &-~7x_{5}&+~{\underline {\mathbf {2x_{4}} }}&)~/~1\end{matrix}}}$

According to the cycle-free rule in the previous example, we would now have to choose to expose. Instead, we follow the modified rule and choose the basic variable for it , which leads to the following system: ${\displaystyle \,x_{1}\,}$ ${\displaystyle \,x_{4}\,}$ ${\displaystyle \,x_{6}\,}$

${\displaystyle {\begin{matrix}x_{1}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{5}} }}&+~~x_{6}&)~/~2\\[2pt]x_{2}&=&(&~~~6&-~7x_{5}&-~3x_{6}&)~/~2\\[2pt]x_{3}&=&(&~~~0&-~3x_{5}&-~~x_{6}&)~/~2\\[2pt]x_{4}&=&(&~~~4&+~7x_{5}&+~~x_{6}&)~/~2\end{matrix}}}$

This system of equations again has the same entries as the start system; but because these are still assigned to other variables, the cycle is not finished after these 4 steps. Nevertheless, it is easy to check that the algorithm returns in a total of 6 steps to the start system in the reverse order and in 12 steps to the exact start system. The total system of equations and inequalities actually has no solution at all, but the pivot method cannot find out the one with the upper pivot choice.

The order in which the variables and equations of a pivot system are listed is basically arbitrary. Nevertheless, the first pivot selection strategies, which deal with variables and equations independently of their representation in the pivot system (and were also easy to implement), were only introduced by Bland in 1977.

In the early days of the pivot method (1950–1970), when no strict distinction was made between algorithms and data structures, pivot selection strategies were more likely to be described on the basis of data structures (so-called tableaus ), and with this type of strategy the finiteness of the method was usually possible without additional calculations cannot be guaranteed. If, for example, the considered pivot selection rule is changed in the sense of the originally used Dantzig selection , in which the first of the rows and columns in question is simply selected, then that does not help either. The selection rule would then be

1. Choose the smallest      with    , ${\displaystyle k\!\in \!\{n+1,\ldots ,n+m\}}$ ${\displaystyle b_{\pi (k)}^{\pi }=\min _{i}^{\,}\{b_{\pi (i)}^{\pi }\}<0}$
2. Then choose the smallest      with    , ${\displaystyle l\!\in \!\{1,\ldots ,n\}}$ ${\displaystyle G_{\pi (k),\pi (l)}^{\pi }>0\,}$
3. The Pivot is , ${\displaystyle (x_{\pi (k)},\,x_{\pi (l)})}$

but in the above example this leads into exactly the same endless loop.

duality

Dual task

Each linear optimization task , which in this context is also called the primal task , can be assigned a second optimization task depending on the above book form ; the coefficient matrix of this so-called dual problem is the negative transpose of the coefficient matrix of the original problem:

${\displaystyle {\begin{matrix}w&=&-\;f&-&b_{1}\,y_{n+1}&-&\cdots &-&b_{m}\,y_{n+m}\\[3pt]y_{1}&=&-\;d_{1}&-&G_{n+1,1}\,y_{n+1}&-&\cdots &-&G_{n+m,1}\,y_{n+m}\\\vdots &&\vdots &&\vdots &&&&\vdots \\y_{n}&=&-\;d_{n}&-&G_{n+1,n}\,y_{n+1}&-&\cdots &-&G_{n+m,n}\,y_{n+m}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~w\,,\quad y_{1}\geq 0,\;\ldots ,\;y_{m+n}\geq 0\end{matrix}}}$

In a squat form, this becomes:

${\displaystyle {\begin{matrix}&&w&=&(-f)&+&\sum _{i\in B}\,(-b_{i})\,y_{i}\\[6pt]\forall ~j\in D&&y_{j}&=&(-d_{j})&+&\sum _{i\in B}\,(-G_{i,j})\,y_{i}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~w\,,\quad \forall ~k\in D\cup B\quad y_{k}\geq 0\end{matrix}}}$

(Caution: When deriving from this formulation, it must not be replaced by! Often the dual task is also defined with the objective function instead of , which is feasible but also more confusing.) ${\displaystyle \max \,z,\;\max \,w}$ ${\displaystyle \min \,z,\;\min \,w}$ ${\displaystyle \min \,(-w)}$ ${\displaystyle \max \,w}$

As will be shown in a moment, the maximum of the dual task (if any) is exactly the negative maximum of the primary task.

Gradual conversion

The above relationship of the coefficients between the primal task and the dual task does not only apply to the starting basis, but is retained as long as the basis variables are converted according to the same pivot. It applies

${\displaystyle {\begin{matrix}&&w&=&(-f^{\pi })&+&\sum _{i\in B(\pi )}\,(-b_{i}^{\pi })\,y_{i}\\[6pt]\forall ~j\in D(\pi )&&y_{j}&=&(-d_{j}^{\pi })&+&\sum _{i\in B(\pi )}\,(-G_{i,j}^{\pi })\,y_{i}\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~w\,,\quad \forall ~k\in D\cup B\quad y_{k}\geq 0\,.\end{matrix}}}$

This duality relationship can most easily be seen in a pivot system that contains only two independent unknowns and two exposed unknowns. We get the same system if we first exchange two of the unknowns and then derive the dual task, or if we do these steps in reverse order; the following commutative diagram shows this relationship:

${\displaystyle {\begin{matrix}\delta \,x_{i}&\!=\!&(~~\alpha )&\!\!\!x_{j}&\!+\!&(~~\sigma )&\!\!\!x_{s}\\[6pt]\delta \,x_{r}&\!=\!&(~~\zeta )&\!\!\!x_{j}&\!+\!&(~~p)&\!\!\!x_{s}\end{matrix}}}$	${\displaystyle {x_{r}\leftrightarrow x_{s}}}$	${\displaystyle {\begin{matrix}p\,x_{i}&\!=\!&(\textstyle {\frac {\alpha p\,-\,\zeta \sigma }{\delta }})&\!\!\!x_{j}&\!+\!\!&(~\sigma )&\!\!\!x_{r}\\[6pt]p\,x_{s}&\!=\!&(~-\zeta ~)&\!\!\!x_{j}&\!+\!\!&(~\delta )&\!\!\!x_{r}\\\end{matrix}}}$
${\displaystyle -\,[\cdots ]^{\,T}}$		${\displaystyle -\,[\cdots ]^{\,T}}$
${\displaystyle {\begin{matrix}\delta \,y_{j}&\!=\!&(-\alpha )&\!\!\!y_{i}&\!+\!&(-\zeta )&\!\!\!y_{r}\\[6pt]\delta \,y_{s}&\!=\!&(-\sigma )&\!\!\!y_{i}&\!+\!&(-p)&\!\!\!y_{r}\\\end{matrix}}}$	${\displaystyle {y_{s}\leftrightarrow y_{r}}}$	${\displaystyle {\begin{matrix}p\,y_{j}&\!=\!&(\textstyle {\frac {\zeta \sigma \,-\,\alpha p}{\delta }})&\!\!\!y_{i}&\!+\!\!&(~~\zeta )&\!\!\!y_{s}\\[6pt]p\,y_{r}&\!=\!&(~-\sigma ~)&\!\!\!y_{i}&\!+\!\!&(-\delta )&\!\!\!y_{s}\\\end{matrix}}}$

From the dual relationship it follows that an optimal system for the primary task also provides an optimal system for the dual task.

The task in the first calculation example includes the following dual task (the zeros come from ): ${\displaystyle z=0+0x_{1}+0x_{2}\,}$

${\displaystyle {\begin{matrix}~w~&=&(&0&+~~2y_{3}&+~~4y_{4}&-~~9y_{5}&)~/~1\\[2pt]y_{1}&=&(&0&+~~7y_{3}&+~~5y_{4}&-~~2y_{5}&)~/~1\\[2pt]y_{2}&=&(&0&-~~2y_{3}&-~~2y_{4}&+~~3y_{5}&)~/~1\end{matrix}}}$

${\displaystyle {\begin{matrix}\max ~w,\quad y_{1}\geq 0,\ y_{2}\geq 0,\ y_{3}\geq 0,\ y_{4}\geq 0,\ y_{5}\geq 0\end{matrix}}}$

The above algorithm then leads to the optimal system

${\displaystyle {\begin{matrix}~w~&=&(&0&-~37y_{2}&-~~6y_{1}&-~10y_{3}&)~/~11\\[2pt]y_{4}&=&(&0&+~~2y_{2}&+~~3y_{1}&-~17y_{3}&)~/~11\\[2pt]y_{5}&=&(&0&+~~5y_{2}&+~~2y_{1}&-~~4y_{3}&)~/~11\end{matrix}}}$

and the optimal solution to this is of course for everyone . The primary task had an implicit objective function ; all optimal solutions for the primal and also the dual task would therefore have a target value, if any . This is the same value that the initial solution of the dual task had, but the existence of an optimal solution is not evident from the first system of equations: there could have been solutions with an infinitely large and thus no optimal solution at all. ${\displaystyle x_{k}=0}$ ${\displaystyle k\in D\cup B}$ ${\displaystyle z=0}$ ${\displaystyle w=-z=0}$ ${\displaystyle w}$

Solution pairs

A theoretically significant consequence of the duality theory is: We do not necessarily need a maximization algorithm to solve linear optimization problems; any algorithm that solves systems of linear inequalities is sufficient. From the duality relation it follows that every optimal basis of the original task also directly supplies an optimal basis for the dual task; the optimal value of the target variable is then the negative of the optimal value of  . Accordingly, the following applies to admissible pairs of solutions to the two problems ${\displaystyle w}$ ${\displaystyle z.}$

${\displaystyle z+w~\leq ~(\max z)\!+\!(\max w)~=~(\max z)\!+\!(-\max z)~=~0\,,}$

and applies to optimal solution pairs

${\displaystyle (\max z)\!+\!(\max w)~=~(\max z)\!+\!(-\max z)~=~0\,.}$

From this it follows that the optimal solutions of both tasks are exactly the solutions of the above equation systems with the following inequalities:

${\displaystyle z\,+\,w\,\geq \,0,\qquad \forall ~k\in D\cup B\qquad x_{k}\geq 0,\quad y_{k}\geq 0.}$

That is written out

${\displaystyle {\begin{matrix}\sum _{j\in D}\,d_{j}\,x_{j}~~+~~\sum _{i\in B}\,(-b_{i})\,y_{i}~~\geq ~~0\\[6pt]\forall ~j\in D\quad y_{j}~=~(-d_{j})~+~\sum _{i\in B}\,(-G_{i,j})\,y_{i}\\[6pt]\forall ~i\in B\quad x_{i}~=~b_{i}~+~\sum _{j\in D}\,G_{i,j}\,x_{j}\\[6pt]\forall ~k\in D\cup B\qquad x_{k}\geq 0,\quad y_{k}\geq 0\end{matrix}}}$

In practice, such a procedure is of course only competitive if the common data structure of both tasks is also used.

Special pivot procedure

The simplest of all pivot methods belong to the criss-cross methods , which were developed in the 1980s for tasks in the context of oriented matroids . The much more complex simplex methods were published by George Dantzig as early as 1947 for the solution of linear optimization problems and, thanks to their widespread use, have significantly motivated the search for criss-cross methods. Further pivot methods have been developed for the linear complementarity problem with sufficient matrices (including quadratic programming) and for linear-fractional optimization problems.

When working out different pivot procedures, the main thing is to keep the number of pivot steps and thus the duration of the procedure low. While the currently known simplex methods all require an over- polynomially limited runtime - that is a runtime that cannot be limited by a polynomial in the data storage size - runtime bounds for the criss-cross methods are an open research topic (until 2010). In summary, it can be said that criss-cross methods have more degrees of freedom than simplex methods, and that precisely for this reason a criss-cross method can be faster with a good pivot selection and slower with a poor pivot selection than simplex methods.

Primal simplex method

→ Main article : Simplex method

Primal simplex methods (mostly just called simplex methods ) assume a so-called admissible basis with for all and only examine admissible bases until an optimal basis is found. An important property of the primal simplex method is that the value of the target variable, that is , increases monotonically with each step ; if it were to grow strictly monotonously, the finiteness of the process would be assured. ${\displaystyle b_{i}^{\pi }\geq 0}$ ${\displaystyle i\in B(\pi )}$ ${\displaystyle f^{\pi }}$

A primal simplex method has to choose its pivots as follows:

1. Pick any one that satisfies. For example, find the smallest with this property (Bland's rule). ${\displaystyle s\in D(\pi )}$ ${\displaystyle d_{s}^{\pi }>0}$ ${\displaystyle s\in D(\pi )}$
2. Pick any one that satisfies. For example, find the smallest with this property (Bland's rule). ${\displaystyle r\in B(\pi )}$ ${\displaystyle b_{r}^{\pi }/(-G_{r,s}^{\pi })=\min {}_{i\in B(\pi )}\{b_{i}^{\pi }/(-G_{i,s}^{\pi })~|~G_{i,s}^{\pi }<0\}}$ ${\displaystyle r\in B(\pi )}$

In order to obtain a valid starting point, an auxiliary task must be solved in a so-called phase 1 . This can be done by inserting a new objective function with any non-positive entries and by maximizing the dual task for which the starting solution is now permissible. From a statistical point of view, it is advantageous to randomly select the entries of the new objective function negatively.

A standard result of linear optimization says that for every solvable task and for every admissible base there is a sequence of allowed pivots that leads to an optimal basis using only admissible bases; However, it is not known whether there is a sequence of this type whose length can be restricted polynomially in the memory size of the data.

Dual simplex processes

Dual simplex method are Pivot procedures described by a so-called dual-permissible basis to all go out and investigate in their search for an optimum basis exclusively dual-permissible bases; the value of the target variable decreases monotonically. ${\displaystyle d_{j}^{\pi }\leq 0}$ ${\displaystyle j\in D(\pi )}$

A dual simplex method chooses its pivots as follows: ${\displaystyle (x_{r},\,x_{s})}$

1. Pick any one that satisfies. For example, find the smallest with this property (Bland's rule). ${\displaystyle r\in B(\pi )}$ ${\displaystyle b_{r}^{\pi }<0}$ ${\displaystyle r\in B(\pi )}$
2. Pick any one that satisfies. For example, find the smallest with this property (Bland's rule). ${\displaystyle s\in D(\pi )}$ ${\displaystyle (-d_{s}^{\pi })/G_{r,s}^{\pi }=\min {}_{j\in D(\pi )}\{(-d_{j}^{\pi })/G_{r,j}^{\pi }~|~G_{r,j}^{\pi }>0\}}$ ${\displaystyle s\in D(\pi )}$

Dual simplex processes generate the same pivot sequences as the primal simplex processes applied to the dual task and therefore basically have the same properties as the primal processes. The fact that they are nevertheless preferred to the primal method for solving many applied tasks is due to the fact that it is easier to find a dual-permissible starting basis for many applied tasks.

Criss-cross method

Criss-Cross method (English: criss-cross ) are common pivot processes which start from an arbitrary basis; As a rule, this name is used for combinatorial pivot methods, that is, for pivot methods which only take into account the signs of the system coefficients and not the coefficients themselves for pivot selection.

The best-known of all criss-cross methods extends the smallest index pivot selection from the first example. To do this, the unknowns are arranged in a more or less fixed order and the pivots are selected as follows (as usual, the minimum of the empty set is infinitely large):

1. Find the indices and . ${\displaystyle r=\min\{i\in B(\pi )~|~b_{i}^{\pi }<0\}}$ ${\displaystyle s=\min\{j\in D(\pi )~|~d_{j}^{\pi }>0\}}$
2. If is, choose Pivot with . ${\displaystyle r<s}$ ${\displaystyle (x_{r},\,x_{l})}$ ${\displaystyle l=\min\{j\in D(\pi )~|~G_{r,j}^{\pi }>0\}}$
3. If is, choose Pivot with . ${\displaystyle s<r}$ ${\displaystyle (x_{k},\,x_{s})}$ ${\displaystyle k=\min\{i\in B(\pi )~|~G_{i,s}^{\pi }<0\}}$

This of course leaves the question of how the variables should be arranged.

Example of a criss-cross method

In the following example we are using the Smallest Index Pivot Selection above. The aim is to find values ​​for the variables that make up the system of equations ${\displaystyle x_{1}\geq 0,\ldots ,x_{5}\geq 0}$

${\displaystyle {\begin{matrix}z&=&(&~~~0&+~\mathbf {3x_{1}} &+~2x_{2}&)~/~1\\[2pt]x_{3}&=&(&~~~3&-~{\underline {\mathbf {2x_{1}} }}&-~~x_{2}&)~/~1\\[2pt]x_{4}&=&(&~~~7&-~2x_{1}&-~3x_{2}&)~/~1\\[2pt]x_{5}&=&(&~~~4&-~3x_{1}&-~~x_{2}&)~/~1\end{matrix}}}$

meet and thereby bring the additional target variable to a maximum. We use the pivot selection of the smallest index mentioned above. ${\displaystyle z}$

All pivots are allowed in our original system; However, the selection rule stipulates that we expose and exchange for: ${\displaystyle x_{1}}$ ${\displaystyle x_{3}}$

Base 0 to base 1 (scalable and animated by Firefox when clicking twice and holding down)

This leads to the new system of equations:

${\displaystyle {\begin{matrix}z&=&(&~~~9&-~3x_{3}&+~~\mathbf {x_{2}} &)~/~2\\[2pt]x_{1}&=&(&~~~3&-~~x_{3}&-~~{\underline {\mathbf {x_{2}} }}&)~/~2\\[2pt]x_{4}&=&(&~~~8&+~2x_{3}&-~4x_{2}&)~/~2\\[2pt]x_{5}&=&(&-~1&+~3x_{3}&+~~x_{2}&)~/~2\end{matrix}}}$

Here the pivots , and , are allowed; based on the selection rule, we disclose instead of : ${\displaystyle (x_{2},\,x_{1})}$ ${\displaystyle (x_{2},\,x_{4})}$ ${\displaystyle (x_{5},\,x_{2})}$ ${\displaystyle (x_{5},\,x_{3})}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{1}}$

Base 1 to base 2

We get the system:

${\displaystyle {\begin{matrix}z&=&(&~~~6&-~2x_{3}&-~~x_{1}&)~/~1\\[2pt]x_{2}&=&(&~~~3&-~~x_{3}&-~2x_{1}&)~/~1\\[2pt]x_{4}&=&(&-~\mathbf {2} &+~3x_{3}&+~{\underline {\mathbf {4x_{1}} }}&)~/~1\\[2pt]x_{5}&=&(&~~~1&+~~x_{3}&-~~x_{1}&)~/~1\end{matrix}}}$

The allowed pivots of this system of equations are and ; we therefore disclose instead of : ${\displaystyle (x_{4},\,x_{1})}$ ${\displaystyle (x_{4},\,x_{3})}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{4}}$

Base 2 to base 3

Now we get the system:

${\displaystyle {\begin{matrix}z&=&(&~~22&-~5x_{3}&-~~x_{4}&)~/~4\\[2pt]x_{2}&=&(&~~~8&+~2x_{3}&-~2x_{4}&)~/~4\\[2pt]x_{1}&=&(&~~~2&-~3x_{3}&+~~x_{4}&)~/~4\\[2pt]x_{5}&=&(&~~~2&+~7x_{3}&-~~x_{4}&)~/~4\end{matrix}}}$

This system of equations is optimal; are the values ​​of the unknowns for the corresponding solution

${\displaystyle z=22/4=5.5,x_{1}=2/4=0.5,x_{2}=8/4=2.0,x_{3}=0,x_{4}=0,x_{5}=2/4=0.5\,.}$

Big jobs

An implementation of the pivot method for practical tasks is often far from trivial. The entries of large systems of equations - with tens of thousands of variables - almost always have some structure that needs to be exploited to perform the calculation quickly and with few rounding errors:

• In the start system of large tasks (not in the converted systems of equations) the overwhelming majority of the entries are zero (the system is sparsely populated ), which makes it possible to save a large part of the calculations if one also partially starts from the start system in later conversions.
• In the procedures with delayed evaluation (by changing the start matrix, partial LR decomposition of the coefficient matrix, product form of inverse matrices and other things), an entry is only calculated and only when it is really needed to find the pivot. In doing so, however, you often have to fall back on entries from older systems of equations, so that the formulas for calculation become more complicated and diverse.
• For some special structures, such as the network flow problem , particularly efficient implementations have been developed, and these special structures are often embedded in larger systems.

Nevertheless, in practice there are also smaller tasks for which the direct implementation described above makes sense.

literature

• George B. Dantzig : Linear programming and extensions (=  econometrics and corporate research . Volume 2 ). Springer, Berlin et al. 1966 (Original edition: Linear Programming and Extensions. Princeton University Press, Princeton NJ 1963, (PDF; 9.1 MB) ).
• Vašek Chvátal : Linear Programming . Freeman and Company, New York NY 1983, ISBN 0-7167-1587-2 .
• Robert J. Vanderbei: Linear Programming. Foundations and Extensions (=  International Series in Operations Research & Management Science . Volume 114 ). 3. Edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5 ( (PDF; 2.3 MB) , alternative edition: Linear Programming; Foundations and Extensions , Kluwer, ISBN 978-0-7923-9804-2 ).

Individual evidence

1. ↑ ^{a b c d e} Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Vol. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5 .
2. ^ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Vol. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5 , Chapter 21.4: Simplex Method vs Interior-Point Methods.
3. ↑ ^{a b c d e} Vašek Chvátal: Linear Programming. Freeman and Company, New York NY 1983, ISBN 0-7167-1587-2 .
4. ↑ ^{a b} Komei Fukuda, Tamás Terlaky: On the Existence of a Short Admissible Pivot Sequences for Feasibility and Linear Optimization Problems. In: Pure Mathematics and Applications. Vol. 10, 1999, ISSN  1218-4586 , pp. 431-447, ( PDF ).
5. ↑ ^{a b c d} Komei Fukuda, Tamás Terlaky: Criss-cross methods: A fresh view on pivot algorithms. In: Mathematical Programming. Vol. 79, No. 1/3, 1997, ISSN  0025-5610 , pp. 369–395, doi: 10.1007 / BF02614325 , ps file  ( page no longer available , search in web archives )  Info: The link was automatically defective marked. Please check the link according to the instructions and then remove this notice. .  
6. ^ ^{A b c} Robert G. Bland: New finite pivoting rules for the simplex method. In: Mathematics of Operations Research. Vol. 2, No. 2, pp. 103-107, doi: 10.1287 / moor.2.2.103 .
7. ↑ Shuzhong Zhang: New variants of finite criss-cross pivot algorithms for linear programming. In: European Journal of Operations Research. Vol. 116, No. 3, 1999, ISSN  0377-2217 , pp. 607-614, doi: 10.1016 / S0377-2217 (98) 00026-5 , (PDF; 164.4 kB) .
8. ↑ Komei Fukuda & Bohdan Kaluzny: The criss-cross method can take Ω (n ^d ) pivots. In: Proceedings of the Twentieth Annual Symposium on Computational Geometry (SCG '04). June 9-11, 2004, Brooklyn, New York, USA. ACM Press, New York NY 2004, ISBN 1-58113-885-7 , pp. 401-408, doi: 10.1145 / 997817.997877 , ps file ( memento of the original from September 17, 2013 on the Internet Archive ) Info: The archive link was inserted automatically and not yet tested. Please check the original and archive link according to the instructions and then remove this notice. . 
9. ^ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Vol. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5 , Chapter 8: Implementation Issues.
10. ^ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Vol. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5 , Chapter 13: Network Flow Problems.

Web links

• Interactive pivot method applet by Robert Vanderbei from 1997. The applet allows the user to set up a linear system of equations with exposed basic variables and then to rearrange any variables of this system of equations. Although the applet is called "Simplex Pivot Tool", it is designed for very general pivot methods. The coefficients can also be viewed as fractions without rounding, but are not brought to a common denominator.
• Additional information (English) on the criss-cross method .