Game theory
The game theory is a mathematical theory in which decision-making situations are modeled, in which several parties interact. Among other things, she tries to derive the rational decision-making behavior in social conflict situations from this. Game theory is originally a branch of mathematics . It serves a variety of fields of application .
This article deals with non-cooperative game theory, which is to be distinguished from cooperative game theory . Below are some notes on the differences .
Concept and delimitation
A game in the sense of game theory is a decision-making situation with several participants who influence each other with their decisions . In contrast to classical decision theory , this theory models situations in which the success of the individual depends not only on their own actions but also on that of others (interdependent decision-making situation).
The term game theory (Engl. Game theory ) arose from previously used by the founders term circumlocutions like Theory of games (1928) and theory of games (1944). Although economic applications were formulated as the primary objective as early as the publications of 1928 and 1944, there are multiple references to implications for board games such as chess , bluffing in poker , baccarat and signaling in bridge . Later authors also used board games as examples, for example for John Forbes Nash in his dissertation from 1950, in which he carried out a calculation for a three-person poker as a simple example, following a proof of existence for the equilibrium named after him . In later times, the term interactive decision theory was repeatedly found to be more appropriate than game theory in German-speaking countries. However, due to the widespread use of the term game theory , such proposals could not prevail.
The term game theory also appears in other areas of theoretical treatment of games - see game science , game education , ludology or homo ludens .
application
Game theory is less of a coherent theory than more of a set of analytical tools. Game theory is primarily used in operations research , in economics (both economics and business administration ), in the economic analysis of law (law and economics) as a sub-area of law , in political science , in sociology , in psychology , in in computer science , in linguistic text analysis and, since the 1980s , in biology (especially evolutionary game theory ).
Cooperative vs. non-cooperative game theory
In general, the non-cooperative and the cooperative game theory are differentiated as follows: If the players can conclude binding contracts, one speaks of cooperative game theory. On the other hand, are all behaviors (including possible cooperation between players) self-enforcing , i.e. This means that they result from the self-interest of the players, without binding contracts being able to be concluded, one speaks of non-cooperative game theory.
Cooperative game theory is to be understood as an axiomatic theory of coalition functions (characteristic functions) and is payoff-oriented. Non-cooperative game theory, on the other hand, is action or strategy-oriented. The non-cooperative game theory is a branch of microeconomics , while the cooperative game theory is a branch of its own kind. Well-known concepts of cooperative game theory are the core, the Shapley solution and the Nash negotiation solution .
The non-cooperative game theory plays a bigger role in university teaching than the cooperative game theory. There are many textbooks on game theory and there are many courses at universities with the title game theory, in which cooperative game theory is not dealt with at all or only marginally. Although Nobel Prize winners Robert J. Aumann and John Forbes Nash Jr. both made crucial contributions to cooperative game theory, the prize was specifically awarded by the Nobel Prize Committee for their contributions to non-cooperative game theory.
Nevertheless, the current research continues to examine cooperative game theory, and a large number of new game theoretical scientific articles can be assigned to cooperative game theory. The continued great importance of cooperative game theory in research can also be seen from the fact that research fields that are very present in the scientific discussion, such as negotiation theory and matching theory , are largely analyzed using the means of cooperative game theory.
history
starting point
The historical starting point of game theory is the analysis of Homo oeconomicus , in particular by Bernoulli , Bertrand , Cournot (1838), Edgeworth (1881), von Zeuthen and von Stackelberg . However, these game theory analyzes were always answers to specific questions without a more general theory for analyzing strategic interaction having been developed from them. The first general considerations were made by Émile Borel in 1921.
Basics
It was not until the formalized analysis of parlor games and the proof of the Min-Max theorem by John von Neumann in 1928 that the basis of modern game theory was laid. John von Neumann quickly recognized the applicability of the approach he had developed for analyzing economic issues, so that in 1944 in the book " Theory of Games and Economic Behavior ", which he wrote together with Oskar Morgenstern , there was already an amalgamation between the mathematical theory and economic application. This book is still considered a groundbreaking milestone today. At first a solution was only available for constant sum games. The Nash equilibrium did not offer a general solution until 1950. After that, game theory only gradually established itself as a recognized methodology in economics and, more and more, in neighboring social science disciplines.
Further development
Since 1970 there has been a very rapid development in game theory and an escalation into other disciplines. In this sense, since then the combinatorial and the algorithmic game theory emerged as very mathematically oriented branches as well as the evolutionary game theory , which deviates most strongly from the assumption of conscious decisions.
Appreciation
The Nobel Prize in Economics has been awarded eight times for work in game theory, which illustrates the great importance of game theory for modern economic theory: in 1994 to John Forbes Nash Jr. , John Harsanyi and Reinhard Selten , in 1996 to William Vickrey , in 2005 to Robert Aumann and Thomas Schelling and 2012 to Alvin Roth and Lloyd S. Shapley . For their study of bounded rationality received Herbert A. Simon in 1978, Daniel Kahneman the 2002 Nobel Prize. The awards to Leonid Hurwicz , Eric S. Maskin and Roger B. Myerson in 2007 for their research in the field of mechanism design theory are also closely related to questions of game theory.
methodology
Model interaction as a game
Game theory models a wide variety of situations as one game. The term "game" is to be taken literally: The mathematical-formal description defines which players are there, which sequential course the game has and which options (moves) are available to each player in the individual stages of the sequence.
Examples: In the game of Cournot Duopoly , the players are the companies and their respective option for action is their supply. In the Bertrand duopoly , the players are again the duopolyists, but their options for action are the offer prices. In the game Prisoner's Dilemma , the players are the two prisoners and their sets of actions are statements and are silent . In political science applications, the players are often political parties or lobby groups , while in biology the players are mostly genes or species.
The description of a game also includes a payout function: This function assigns a payout vector to each possible outcome of the game. That is, this vector determines what profit a player makes when a certain outcome of the game occurs. In the case of applications in economics, the payout is mostly to be understood as a monetary variable, whereas in political science applications it can be votes, while in biological applications the payout usually consists of reproductive ability or survivability.
One can see two important aspects in game theory:
- Formalization
- An important step is to formalize a game in terms of game theory . Game theory has developed a rich language for this. See under: Game display
- solution
- Depending on the context , you can try to predict the outcome of the game in a further step. See: Solution Concepts .
An important technique in finding equilibria in game theory is looking at fixed points .
In computer science , one tries to solve certain games, such as chess , SameGame , Mancala , Go , or, for example , to solve certain games with the help of search strategies and heuristics (in general: techniques of combinatorial optimization and artificial intelligence ) . B. to prove that the one who starts always wins with the right strategy (this is e.g. the case for four wins , qubic and five in a row ) or z. B. the one who has the second move can always achieve at least one tie (example mill ). In this context, one speaks of the first movers advantage or second movers advantage .
Concept of information
The player's level of information is decisive for the presentation and solution. A distinction is made here between three terms: complete , perfect (or perfect ) information and perfect memory , depending on whether the player is informed about the rules of the game, the moves of the other players and his own information from the past. Standard is the game with complete information and perfect memory . Perfect information is not a standard assumption as it would be a hindrance to explaining many simple conflicts.
Complete information , the knowledge of all players about the rules of the game, is an assumption that one will generally consider to be a prerequisite for playing together when playing in the classic sense of the word (see game ). Disagreements about the rules of the game, such as whether Mensch ärgere Dich is not obliged to hit an opponent's pin if this is possible on the move in question, or whether a card drawn can be placed immediately if it fits, in Mau Mau usually considered a serious malfunction if not resolved before the game. On the other hand, game theory is applied to many situations for which this information requirement would be too rigid, as the availability of certain information cannot be expected (e.g. in the case of political decisions). That is why it makes sense to expand classical game theory, which works with complete information , to include the possibility of incomplete information . On the other hand, this field is limited because for every game with incomplete information, a game with complete information can be constructed that is strategically equivalent.
Perfect information , i.e. the knowledge of all players about all moves of all players, is a rigorous requirement that is not met in many classic games: For example, it is injured in most card games because the random player's move and the distribution of hands are unknown at the start of the game is because you can only see your own cards at a time. This is why game theory models usually do not assume perfect information . If a game fulfills the criterion of perfect information, it is generally easier to solve in principle ; even if in reality, as in chess, there are great hurdles due to the complexity .
Perfect memory is the knowledge of every player about all information that was already available to him in the past. Although this assumption always seems to be fulfilled at first glance, at least in principle, there are counterexamples: If a game is a team of cooperating players like in skat, "the" individual player no longer knows the individual at the time of their own decision Information context of past moves that a partner made on the basis of his cards.
Forms of representation
Games are usually described either in a strategic (normal) form or in an extensive form . The normal agent form must also be mentioned. Since there are games that none of these forms do justice to, more general mathematical or linguistic descriptions must sometimes be used.
The extensive form
In game theory , the extensive form of a game describes a form of representation of games that is based on the tree representation to illustrate the chronological sequence of decisions.
The normal form
The normal form of a game is essentially limited to the a priori strategy amounts of the individual players and a payout function as a function of the chosen strategy combinations. This form of representation is best suited to games in which all players define their strategies at the same time and without knowing the choice of the other players. A bimatrix shape is usually used for illustration.
The agent normal form
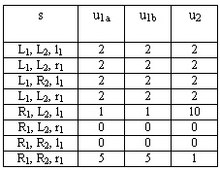
Who or what is a player in a given situation? The normal agent form answers this question as follows: Every move in the course of a game requires a player in the sense of an independent decision maker, since the local interests of a person or institution can diverge from information district to information district. For this purpose, the agent normal form generally has as many players or agents as there are information areas of personal players. The “natural” player 1 is abstracted here, for example, to the agents 1a and 1b.
Solution concepts
Once a game is defined, the analytical tools of game theory can then be used to determine, for example, what the optimal strategies are for all players and what the outcome of the game will be if those strategies are used.
So-called solution concepts are used to analyze problems in game theory.
Equilibria
By far the most prominent solution concept, the Nash equilibrium , comes from John Forbes Nash Jr. (1950). The above question - which possible outcomes a game has if all players behave optimally individually - can be answered by determining the Nash equilibria of a game: The set of Nash equilibria of a game contains, by definition, those strategy profiles in which a individual player could not improve by exchanging his strategy for another strategy given the strategies of the other players.
Further equilibria
There are other solution concepts for other questions. Important are the minimax equilibrium , the repeated deletion of dominated strategies as well as subgame perfection and, in cooperative game theory, the core, the nucleolus , the amount of negotiation and the amount of imputation .
Mixed vs. pure strategies
While a player's pure strategy is a function that assigns an action to each game level where the player's action set is not empty, a mixed strategy is a function that assigns an action to every game level where the player's action set is not empty Probability distribution over the action set available in this level. A pure strategy is thus the special case of a mixed strategy, in which whenever the action set of a player is not empty, the entire probability mass is placed on a single action of the action set. One can easily show that any game whose action sets are finite must have a Nash equilibrium in mixed strategies. In pure strategies, however, the existence of a Nash equilibrium is not guaranteed for many games. The analysis of equilibria in mixed strategies was greatly advanced by a number of contributions by John Harsanyi in the 1970s and 1980s.
Some particular problems
In the following, some problems will be named on the basis of the game forms described and their solution concepts, which have proven to be particularly influential in the game theory treatment.
One-time vs. repeated games
A game that is not repeated after being played once is called a one-shot game . If a one-shot game is carried out several times in a row, the total payout for each player generally being the result of the (possibly discounted) payouts for each individual one-shot game, this is referred to as a repeated game. The entire sequence of all one-shot games is called a super game . In game theory, a distinction is also made between finitely repeated and infinitely repeated super games.
The analysis of repeated games was greatly advanced by Robert J. Aumann .
A solution concept for many finally repeated games is the so-called backward induction , in which the solution of the last one-shot game is first determined and the solutions of the previous games up to the first game are determined on this basis. A well-known application of backward induction is the so-called chainstore paradox .
Incomplete information and reputation
If a player only knows his own type, while others only have probabilistic expectations in this regard, one speaks of incomplete, especially asymmetrical information. Reputation effects always occur when a player can be identified to others as belonging to a certain type.
Well-known rules of the game
Game theory initially not only assumes rationality for every player, but also that all players know that all players are rational, etc. One therefore assumes generally known rules of the game or generally known rationality. In contrast to “perfect” rationality, game theories are increasingly being formulated with limited rationality , which may also allow doubts about the rationality of players (including in evolutionary game theory).
Evolutionary game theory
Of evolutionary game theory one speaks mostly when the behavior of the players is not derived by rational decision calculi but is justified as a result of cultural or genetic evolution processes. The stable results can often be characterized by static stability concepts. One such concept is the evolutionarily stable strategy , also known as "ESS" for short (Maynard Smith and Price, 1973). In evolutionary terms, this game theory says that only the best adapted strategy or mutant can survive.
Game theory and mechanism design
Game theory studies how rational players play a given game. In the mechanism design theory , however, this question is reversed, and an attempt is made to design a corresponding game for a desired result in order to determine or determine the outcome of certain rule-related processes. This is done in the course of solving a mechanism design problem. This procedure can be used not only for "pure" games, but also for the behavior of groups in business and society.
reception
Game theory allows social conflict situations called strategic games to be represented in a multifaceted way and to be resolved mathematically in a strict manner. Due to the unrealistic model assumptions, the empirical explanatory power of game theory is usually denied. No human will ever be as rational as it is assumed by the game theory solution concepts for the players. Humans are always subject to cognitive limitations that exclude perfectly rational behavior in complex games. In the opinion of the Bamberg political scientist Reinhard Zintl, however, a distinction must be made between the application as a behavioral theory and that as a constitutional theory; and, depending on the explanation problem, an inconsistent use of individual actor models is entirely permitted and appropriate.
Examples
Famous problems
- Prisoner's Dilemma
- Feiglingsspiel ( English chicken game )
- Deer hunting
- Falcon dove game
- Battle of the sexes
- Ultimatum game
- Ice cream seller on the beach problem (Hotelling's law)
- Beauty contest
- Triell
- Braess paradox
- Division problem
- Trust game
- Tragedy of the commons
- Dollar auction
- Matching pennies
Famous strategies
Trigger strategies:
- Tit for Tat ( Quid pro quo )
- Tit for Two Tats
- Grim
See also
- Quantum game theory
- Ehrenfeucht-Fraïssé games in model theory
- game semantics / dialogic logic
- Reputation (game theory)
- Strategy (game theory)
- Unpredictability (game theory)
- Graph games
- Pendulum arbitration
literature
- Christian Rieck: Game Theory - An Introduction . Rieck, Eschborn 2012, ISBN 978-3-924043-91-9 .
- Florian Bartholomae, Marcus Wiens: Game Theory - An application-oriented textbook . Springer Gabler Verlag, Wiesbaden 2016, ISBN 978-3-8349-4419-1 .
- Michael Sauer: Operations Research compact . Oldenbourg Verlag, Munich 2009, ISBN 978-3-486-59082-1 .
- Jörg Bewersdorff : Luck, Logic and Bluff: Mathematics in Play - Methods, Results and Limits . 5th edition. Vieweg + Teubner Verlag, Wiesbaden 2010, ISBN 3-8348-0775-3 , doi : 10.1007 / 978-3-8348-9696-4 (deals with applications to board games and historical development).
- Andreas Diekmann : Game theory: introduction, examples, experiments . Rowohlt's Encyclopedia, Reinbek near Hamburg 2009, ISBN 978-3-499-55701-9 .
- Steven N. Durlauf, Lawrence E. Blume: Game Theory. Palgrave Macmillan, 2010, ISBN 978-0-230-23890-9 .
- Manfred Eigen , Ruthild Winkler: The game . Piper, Munich 1987, ISBN 3-492-02151-4 (game theory in the scientific environment, reissued 2010: ISBN 978-3-924043-95-7 ).
- Len Fisher: Scissors, rock, paper. Game theory in everyday life. from the English by Andreas Held. Spektrum Akademischer Verlag, Heidelberg 2010, ISBN 978-3-8274-2467-9 .
- Drew Fudenberg, Jean Tirole: Game Theory . MIT Press, Cambridge / MA 1991, ISBN 978-0-262-06141-4 .
- Robert Gibbons: A prime in game theory . Harvester Wheatsheaf, New York 1992, ISBN 0-7450-1159-4 .
- Herbert Gintis : Game theory evolving. 2nd edition Princeton University Press, Princeton 2009, ISBN 978-0-691-14050-6 .
- Manfred J. Holler, Gerhard Illing: Introduction to game theory . 6th edition. Springer Verlag, Berlin 2005, ISBN 3-540-27880-X .
- Alexander Mehlmann: Strategic Games for Beginners - A playful, formal introduction to methods, models and applications of game theory. (Series: Mathematics for Beginners). Vieweg + Teubner, 2007, ISBN 978-3-8348-0174-6 .
- Roger B. Myerson: Game Theory. Analysis of Conflict. Harvard University Press 1991, ISBN 0-674-34115-5 .
- John von Neumann , Oskar Morgenstern : Theory of Games and Economic Behavior . University Press, Princeton NJ 2004, ISBN 0-691-11993-7 (first published in 1944, considered the first systematic publication on game theory).
- Wolfgang Ortmanns : Decision and game theory: an application-oriented introduction . Verlag Wissenschaft & Praxis, Sternenfels 2008, ISBN 978-3-89673-489-1 .
- Martin J. Osborne, Ariel Rubinstein : Bargaining and Markets . Academic Press, San Diego 1990, ISBN 0-12-528631-7 .
- Martin J. Osborne, Ariel Rubinstein: A Course in Game Theory . MIT Press, 1994, ISBN 0-262-65040-1 .
- Guillermo Owen: Game Theory . Academic Press, San Diego 1995, ISBN 0-12-531151-6 .
- Burkhard Rauhut , Norbert Schmitz and Ernst-Wilhelm Zachow: Game theory . Teubner, Stuttgart 1979.
- Anna Karlin, Yuval Peres : Game theory, Alive, American Mathematical Society 2017, pdf
- Michael Maschler, Eilon Solan, Shmuel Zamir: Game Theory, Cambridge University Press 2013
Web links
- Don Ross: Game Theory. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
- Till Grüne-Yanoff: Game Theory. In: Internet Encyclopedia of Philosophy .
- Lecture notes introduction to game theory by Prof. Dr. Leininger (TU Dortmund)
- Open Yale Courses : ECON 159: Game Theory - Lectures for download (24 × 75 minutes) from Yale University
- Games and AI Group of the Department of Computer Science at Maastricht University (English) - Computer-aided strategies in parlor games
- Gametheory.net (English)
- Wikiludia
- Gambit - software for analyzing finite, strategic and extensive games
- Spieltheorie-Software.de ( Memento from July 18, 2013 in the Internet Archive ) - A software, programmed in Java, for playing and for the extensive analysis of 2-person games
- Professor Rieck's Game Theory Page - Simple examples and explanations of game theory
Individual evidence
- ^ A b John von Neumann: On the theory of parlor games , Mathematische Annalen, Volume 100, 1928, pp. 295-320, doi: 10.1007 / BF01448847 , online (freely accessible) .
- ↑ John von Neumann, Oskar Morgenstern: Theory of games and economic behavior , Princeton 1944.
- ↑ Axel Ockenfels : Keyword game theory in the Gabler Wirtschaftslexikon, accessed on April 30, 2018.
- ↑ Jörg Bewersdorff: Luck, Logic and Bluff: Mathematics in Play - Methods, Results and Limits , Springer Spectrum , 6th Edition, Wiesbaden 2012, ISBN 978-3-8348-1923-9 , doi : 10.1007 / 978-3-8348 -2319-9 , p. 246 ff.
- ^ John Nash: Non-cooperative games , 1950, online version ( Memento from September 17, 2012 in the Internet Archive )
- ↑ Bastian Fromen: Fair division in company networks: Suggested solutions based on the cooperative game theory , Springer, Wiesbaden 2013, ISBN 978-3-8244-8164-4 , doi: 10.1007 / 978-3-322-81803-4 , p. 55 in Google Book Search
- ↑ See Reinhard Breymayer : On the pragmatics of the image. Semiotic observations on the debate Mk 12, 13-17 (“Der Zinsgroschen”) taking into account game theory. In: Linguistica Biblica. Interdisciplinary Journal for Theology and Linguistics 13/14 (1972), pp. 19–51.
- ↑ Émile Borel: La théorie du jeu et les equations intégrales à noyau symétrique gauche In: Comptes rendus hebdomadaires des séances de l'Académie des sciences. 173, 1921, pp. 1304-1308 ( gallica.bnf.fr ).
- ^ Maurice Fréchet : Commentary on the Three Notes of Emile Borel. In: Econometrica. Volume 21, Issue 1 (Jan. 1953), pp. 118-124, JSTOR 1906949
- ↑ Reinhard Zintl: The benefit of incomplete explanations: considerations for the social science application of game theory . Lecture given on February 13, 1995 at the Max Planck Institute for the Study of Societies in Cologne ( here (PDF; 32 kB) readable in electronic version).