Dominant strategy

The dominant strategy in game theory models is a strategy that among all possible strategies provides the greatest benefit, regardless of what the other players do (players, agents). The concept of the dominant strategy appears both classical decision theory as well as in game theory and allows behaviors to identify actors in a play. The dominant strategy is used in both simultaneous and sequential games.

Demarcation

The dominant strategy is in contrast to the dominant strategy one of the worst strategies. Again, regardless of what the other players do that dominated strategy is dominated by an ever better, the so-called dominant strategy.

The dominated strategy of a player is of no benefit to him and again does not find a strictly best answer to any strategy of the opponent. If you compare the dominated strategy with the dominant strategy, it becomes clear that the dominant strategy is always better than any other strategy. In contrast, the dominated strategy is always consistently worse than all other strategies. The dominated strategy (s) must therefore be removed.

Definition of terms

The concept of the dominant strategy designates a sequence of actions that is better than all other options, regardless of what the other actors are doing. How one strategy dominates another strategy when the dominant strategy is never worse, but sometimes better than the dominated strategy. A rational actor should not choose a strategy if there is an alternative strategy that is more useful than all possible strategies. If there is a dominant strategy, use it. However, not all actors always have a dominant strategy, not even for one of the actors. Dominance is the exception and not the rule.

Methodology of the dominant strategy

application

In contrast to the sequential game, a simultaneous game is characterized by a lack of communication of the exogenous factors within a game. It can only be played once. In a sequential game, however, the opponent's steps are usually known. This is ensured through communication, although there may still be a certain information asymmetry . Thus, if there is a dominant strategy for every given decision by your opponent, the dominant strategy would always be chosen for sequential moves. However, the opposite case could also occur here, whereby the opponent's turn is only on the second move. Here the opponent can calmly wait for the decision and adapt it to the situation. Here it is advisable to choose a strategy other than the dominant one. In this case, one speaks of self-commitment based on game theory. In the case of sequential moves, using dominant strategies in game theory, the application of cooperative solutions can also be considered.

Strictly / strictly dominant strategy

A player's strategy is a strictly dominant strategy if it is of greater use to him than all of his other strategies in all possible strategy combinations of his fellow players. Since this property can only apply to one strategy at a time, there is at most one strictly dominant strategy for each player. A player with a strictly dominant strategy does not need to cooperate to get the most benefit.

The condition for a strictly dominant strategy can be described by a mathematical formula. Let be the possible strategies of a player and the possible strategy combinations of his fellow players. A player's strategy is called strictly dominant if ${\ displaystyle S_ {i}}$ ${\ displaystyle i}$ ${\ displaystyle S _ {- i}}$ ${\ displaystyle s_ {i} ^ {\ star} \ in S_ {i}}$ ${\ displaystyle i}$

{\ displaystyle (s_ {i} ^ {\ star}, s _ {- i}) \ succ _ {i} (s_ {i}, s _ {- i})}

applies to all other strategies of the player and all strategy combinations of his fellow players. This means that players value the left strategy combination higher than the right one. ${\ displaystyle s_ {i} \ in S_ {i} \ setminus \ {s_ {i} ^ {\ star} \}}$ ${\ displaystyle s _ {- i} \ in S _ {- i}}$ ${\ displaystyle \ succ _ {i}}$ ${\ displaystyle i}$

If there is a utility function in a game and a player has a strictly dominant strategy, then this strategy is the one with the highest payout for him.

Application example

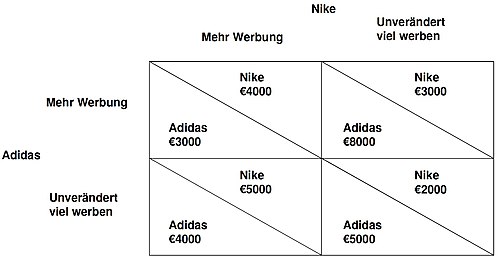
The scenario in Figure 1 shows the two competing sporting goods manufacturers Nike and Adidas , which, depending on the decision-making strategy, could potentially change their sales by using more advertising. The goal of both is to maximize sales.

Figure 1 - Nike's strictly dominant strategy versus Adidas

For Nike it is definitely better to invest more advertising in order to increase sales: If Adidas also invests in more advertising, Nike still achieves increased sales of 4,000 euros. However, if Adidas continues to use a lot of advertising, Nike achieves even higher sales of 5000 euros. Nike could, however, opt for the same amount of advertising , but would therefore accept lower sales than if more advertising were used.

No matter what Adidas does: It is definitely better for Nike to invest more advertising . For Nike, the strategy of more advertising is strictly the best answer to every conceivable strategy of Adidas. The Alternative same amount of advertising will be more advertising of the alternative dominates . The alternative of more advertising is therefore a strictly dominant strategy for Nike .

Weakly dominant strategy

A player's strategy is a weakly dominant strategy if it has the greatest benefit for him in all possible strategy combinations of his fellow players. In general, a player can have several dominant strategies that all have the same benefit for him. A player with a weakly dominant strategy does not need to cooperate to get the most benefit.

The condition for a weakly dominant strategy can be described by a mathematical formula. A player's strategy is called weak dominant if ${\ displaystyle s_ {i} ^ {\ star} \ in S_ {i}}$ ${\ displaystyle i}$

{\ displaystyle (s_ {i} ^ {\ star}, s _ {- i}) \ succeq _ {i} (s_ {i}, s _ {- i})}

for all other strategies of the player and all strategy combinations of his fellow players and ${\ displaystyle s_ {i} \ in S_ {i}}$ ${\ displaystyle s _ {- i} \ in S _ {- i}}$

{\ displaystyle (s_ {i} ^ {\ star}, s _ {- i} ^ {\ prime}) \ succ _ {i} (s_ {i}, s _ {- i} ^ {\ prime})}

applies to at least one of these strategy combinations. This means that players value the strategy combination on the left at least as highly as the one on the right. ${\ displaystyle s _ {- i} ^ {\ prime} \ in S _ {- i}}$ ${\ displaystyle \ succeq _ {i}}$ ${\ displaystyle i}$

If there is a utility function in a game and a player has weakly dominant strategies, then those strategies will have the highest payout for him.

Application example

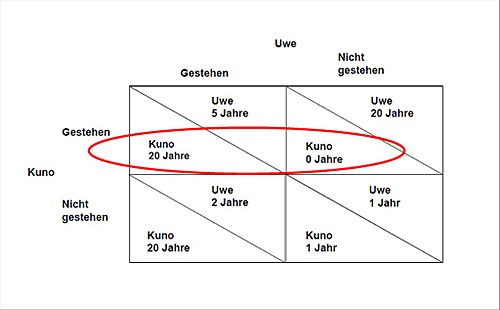
The prisoner's dilemma scenario, shown in Figure 2, is based on two defendants who have actually committed a crime . The prison sentences can vary depending on the decision-making strategy. This is a simultaneous game in which the defendants are not entitled to be informed of each other's decision. The goal of both is to minimize their own prison sentence.

Figure 2 - Kuno's weak dominant strategy towards Uwe

It can be stated that there is no strictly dominant strategy for Kuno : If Uwe did not confess, it would be best for Kuno to confess. If Uwe chooses to confess, then both strategies are equally good for Kuno. Kuno is indifferent between confess and not confess. So it can be stated that for Kuno the strategy to confess is never worse than not to confess the strategy; in the event that Uwe does not confess, even better. After identifying the weakly dominated strategy not to confess, it can be assumed that Kuno will confess .

Solution concepts in dominant strategies

The dominant strategy represents a solution concept in game theory . If every player has a strictly dominant strategy in a game, it is rational for every player to play this strategy configuration as a non-cooperative solution. However, this does not guarantee that the resulting payouts will be collectively rational as well. Due to the composition of the rationally chosen strategy combination, the game is in a balance of dominant strategies. Each equilibrium of dominant strategies also reveals a Nash equilibrium at the same time .

Another solution to a game in game theory with dominant strategies is the elimination of the dominated strategies. Although the dominated strategy is of no benefit to the respective player, it does provide an opportunity to reduce the complexity of a game. Accordingly, the number of possible game results using the iterative elimination of strictly dominated strategies can limit the number of possible game results. This makes it easier to choose the strategy that maximizes benefits.

literature

Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners . Schaeffer-Poeschel Verlag, Stuttgart 1997, ISBN 3-7910-1239-8 .
Avanish K. Dixit, Susan Skeath: Games of Strategy . 2nd Edition. WW Norton & Company, New York 2004, ISBN 0-393-92499-8 .
Joel Watson: Strategy. An Introduction to Game Theory . 2nd Edition. WW Norton & Company, New York 2008, ISBN 978-0-393-92934-8 .
Prof. Dr. Manfred J. Holler, Prof. Dr. Gerhard Iling: Introduction to game theory . 6th edition. Springer-Verlag Berlin Heidelberg New York, Berlin Heidelberg 2006, ISBN 3-540-27880-X .
Siegfried K. Berninghaus, Karl-Martin Ehrhart, Werner Güth: Strategic games. An introduction to game theory. Springer-Verlag Berlin Heidelberg New York, Berlin Heidelberg 2002, ISBN 3-540-42803-8 .
Thomas Riechmann: Game Theory . 2nd Edition. Verlag Franz Vahlen, Munich 2008, ISBN 978-3-8006-3505-4 .
Thomas Sattler: Introduction to game theory . University of Konstanz, Konstanz 2006, (pdf) .

Web links

Individual evidence

↑ In: Professor Rieck's Game Theory Page Processing status: April 10, 2008 (Accessed: December 28, 2008, 10:09 am CET).
↑ In: Professor Rieck's game theory page, status: April 10, 2008 (accessed: December 18, 2008, 16:22 CET).
↑ See Thomas Riechmann: Spieltheorie , p. 27.
↑ ^a ^b See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 67.
↑ See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 61.
↑ In: Professor Rieck's Game Theory Page Processing status: April 10, 2008 (accessed: January 3, 2009, 13:51 CET).
↑ See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 67.
↑ See Siegfried K. Berninghaus, Karl-Martin Ehrhart, Werner Güth: Strategic Games. An introduction to game theory , p. 18 below.
↑ See Thomas Sattler: Introduction to Game Theory , p. 19, status: November 23, 2006 (accessed: December 20, 2008, 8:12 am CET).

[Spieltheorie_online-1] In: Professor Rieck's Game Theory Page Processing status: April 10, 2008 (Accessed: December 28, 2008, 10:09 am CET).

[Spieltheorie_online2-2] In: Professor Rieck's game theory page, status: April 10, 2008 (accessed: December 18, 2008, 16:22 CET).

[Spieltheorie1-3] See Thomas Riechmann: Spieltheorie , p. 27.

[Spieltheorie_für_Einsteiger3-4] See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 67.

[Spieltheorie_für_Einsteiger2-5] See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 61.

[Spieltheorie_online3-6] In: Professor Rieck's Game Theory Page Processing status: April 10, 2008 (accessed: January 3, 2009, 13:51 CET).

[Spieltheorie_für_Einsteiger4-7] See Avinash K. Dixit, Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners , p. 67.

[Strategische_Spiele-8] See Siegfried K. Berninghaus, Karl-Martin Ehrhart, Werner Güth: Strategic Games. An introduction to game theory , p. 18 below.

[Einführung_in_die_Spieltheorie1-9] See Thomas Sattler: Introduction to Game Theory , p. 19, status: November 23, 2006 (accessed: December 20, 2008, 8:12 am CET).