Backward induction

John von Neumann (1940)

The backward induction is a first of John von Neumann and Oskar Morgenstern (1944) applied game-theoretic solution concept to subgame perfect Nash equilibria in sequential and repeated games work out.

In contrast to the forward induction, the starting point is the last decision node of the last (real) sub- game on the game tree . Accordingly, in the course of the procedure backwards , that is to say in the direction of the first decision node, that path is highlighted which is to generate the maximum payout for the actor. Since this path induces a Nash equilibrium in every subgame, the resulting equilibrium is also subgame perfect.

Requirements for applicability

The necessary and sufficient conditions for the game are:

• it is finite , d. H. there is a limited number of rounds that can be played.
• it is played sequentially, i.e. H. Players act one after the other.
• it can be represented in extensive form , i. H. you can depict it as a play tree.
• its players act under the assumptions of rational behavior , i. H. Actions are chosen to maximize payouts.
• and the players have well-known, mutual knowledge of rational behavior ( common knowledge ); H. every player also knows about the rational behavior of the others and they in turn know that you know it, etc. ( infinite regress )

Modified types of backward induction allow z. B. to bypass the finiteness of the game as a restriction, but are mostly only used in special cases.

procedure

Verbal

1. Compare the payouts of that player Z who, in terms of time, should act on the last decision node in the last sub-game.
2. Choose the one that maximizes the payout and cross out all others. (The game tree then shortens so that the maximizing payout vector for player Z takes the place of the formerly last decision node. The first sub-game is thus solved.)
3. Now consider the possible payouts of player Y at this point, who is to decide next to last. One chooses referring to the previous deletion of the other options , the payout maximizing action for players Y and reduces the game tree again to the actions that a smaller payout would generate for the player who is on the course.
4. Then you carry out this process for the player who was initially third from last, etc.
5. A subgame-perfect balance is obtained when you can no longer effectively cancel any further actions; consequently a mutually best combination of strategies has been found that represents a Nash equilibrium in each sub-game.

Graphic and mathematical illustration

A sequential example

Consider a simply-played sequential game:

• three players i where , ${\displaystyle {\begin{aligned}i\in (X,Y,Z)\end{aligned}}}$

• two actions and two strategies each . ${\displaystyle {\begin{aligned}({\text{Links}}),({\text{Rechts}})\end{aligned}}}$

The game is thus formally defined as: ${\displaystyle G=\lbrace (L_{i}),\dots ,(R_{i});\ u_{i}(L_{X},L_{Y},L_{Z}),u_{i}(L_{X},L_{Y},R_{Z}),\dots ,u_{i}(R_{X},R_{Y},R_{Z})\rbrace }$

The backward induction steps in extensive form:

Comparison of the payouts (u)	Graphs
Diagram 1: The last sub-game (GREEN) is considered: ${\displaystyle {\begin{aligned}u_{Z}(s_{X},s_{Y},L_{Z})=2>0=u_{Z}(s_{X},s_{Y},R_{Z})\end{aligned}}}$
Diagram 2: The second part of the game has been simplified (RED with rational payout from GREEN): ${\displaystyle {\begin{aligned}u_{Y}(s_{X},L_{Y},s_{Z})=2>1=u_{Y}(s_{X},R_{Y},s_{Z})\end{aligned}}}$
Diagram 3: The completely induced game (BLUE with rational payouts from RED and GREEN): ${\displaystyle {\begin{aligned}u_{X}(R_{X},s_{Y},s_{Z})=2>1=u_{X}(L_{X},s_{Y},s_{Z})\end{aligned}}}$

Result

→ The best actions in each case are: Player plays RIGHT, plays LEFT and plays LEFT. ${\displaystyle X\,}$ ${\displaystyle Y\,}$ ${\displaystyle Z\,}$

→ The resulting subgame-perfect Nash equilibrium is : ${\displaystyle t^{\star }=(R_{X},L_{Y},L_{Z})\,}$

Repeated Prisoner's Dilemma

→ Main article : Prisoner's Dilemma

Another good example to illustrate the process is the Prisoner's Dilemma. It is a classic game theory played simultaneously and shows in its repeated form the real and practical applicability of backward induction . It shows the potential for conflict ( Pareto optimality as well as individual vs. collective rationality ), which the backward induction brings with it as a solution concept.

Building a repeated game

The simply repeated (= 2-round) game consists of:

• imperfect information , (multi-element information sets)

• four real sub-games and one fake (the entire game), as well

• two players i with which two actions and cooperate, and defecting, are available ${\displaystyle {\begin{aligned}i\in (1;2)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(K_{1},D_{1})\end{aligned}}}$ ${\displaystyle {\begin{aligned}(k_{2},d_{2})\end{aligned}}}$

• ${\displaystyle {\begin{aligned}2^{5}=32\end{aligned}}}$Strategies: where ${\displaystyle {\begin{aligned}S_{i}=\lbrace (s_{i}^{1},\dots ,s_{i}^{32})\rbrace \end{aligned}}}$ ${\displaystyle {\begin{aligned}s_{1}^{1}=(K_{1},K_{1}K_{1}K_{1}K_{1}),s_{2}^{1}=(k_{2},k_{2}k_{2}k_{2}k_{2}),\dots ,s_{1}^{32}=(D_{1},D_{1}D_{1}D_{1}D_{1}),s_{2}^{32}=(d_{2},d_{2}d_{2}d_{2}d_{2})\end{aligned}}}$

The game is defined as: ${\displaystyle {\begin{aligned}G=\lbrace S_{1},S_{2};u_{i}(s_{1}^{1},s_{2}^{1}),\dots ,u_{i}(s_{1}^{32},s_{2}^{32})\rbrace \end{aligned}}}$

Prisoner's Dilemma played twice

Comparison of the payouts	Graphs
Diagram 4 shows the entire game tree over 2 rounds. The payouts were added up according to the rounds. The 4 sub-games are outlined in green . A Nash equilibrium must now be sought in each of the 4 sub-games. This is particularly easy in the case of the repeated prisoner's dilemma, since it is strictly dominant to defect. Partial result: In each part of the game outlined in green there is only one Nash equilibrium (defect, defect). The payoff associated with this Nash equilibrium is used for further backward induction.
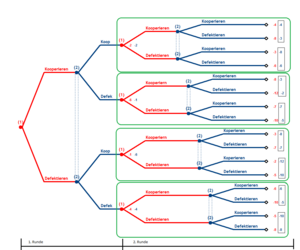
Diagram 5: The game has now been edited to the extent that it depicts the simply played prisoner's dilemma, with the only difference that the payouts represent the Nash equilibria worked out from the sub-games. The last two steps can be summarized. In this combined game, too, defect is strictly dominant, so that again there is only one Nash equilibrium (defect, defect). For the game as a whole, this means that both players will fail at each of their decision nodes. The only subgame-perfect balance is: ${\displaystyle {\begin{aligned}\lbrace (D_{1},D_{1}D_{1}D_{1}D_{1}),(d_{2},d_{2}d_{2}d_{2}d_{2})\rbrace \end{aligned}}}$

Result

→ The game is solved; the subgame perfect Nash equilibrium is: . The players could not exchange information before the game, had no mutual trust and thus could not take any insurance. These in turn would have been necessary in order to arrive at the collectively rational (i.e., simultaneously optimal for all parties) solution with the payout . ( Only gamblers with an affinity for risk would have succeeded in speculative and successful cooperation in these examples , but since we have to assume risk neutrality , elements that are outside the absolute and nominal payout comparison do not play a further role in this process.) ${\displaystyle {\begin{aligned}t^{\star }=(D_{1},D_{1}D_{1}D_{1}D_{1};d_{2},d_{2}d_{2}d_{2}d_{2})\end{aligned}}}$ ${\displaystyle {\begin{aligned}(-6;-6)\end{aligned}}}$

Divergence between theory and empiricism

Differentiation and criticism

The backward induction is a theoretical construct and represents a possibility to solve certain games in the form of subgame-perfect equilibria . However, this type of solution is only to be assessed with regard to the simplicity of the patterns presented above. However, it is not a permanent solution that is always collectively rational or Pareto-optimal . This is also not the task of backward induction . Precisely for this reason one should check the consistency (in the rational sense) of the solutions of every game that were found with this method , as the following examples show:

The department store chain game (Chainstore paradox according to Selten 1978)

→ Main article : Chainstore paradox

In this sequential department store chain game developed by Reinhard Selten , a company dominates the supply market. This monopoly now alternately gets new potential competitors. Competitors have the choice of entering the market ("IN") or not ("OUT"). When a competitor enters, the monopolist can decide whether he will “fight” or “tolerate” him by changing his own prices. The original version of Seltens includes 20 markets and competitors. Seldom created a model on the basis of this game in order to examine the rationality of the behavior of dominant companies when a competitor enters the market.

Chainstore paradox modified to two markets. The competitors (K1, K2) decide whether they want to enter the market or not; the monopolist (M) can fight or tolerate them when they enter. The equilibrium path is marked in green.

The possible actions have the following effects on the payouts:

• "IN": if the competitor enters the market and the monopolist tolerates him, both receive (2); both get (0) if he fights him.
• "OUT": a competitor receives (1) if he stays outside. The monopolist cannot then choose any action, he always receives (5).

procedure

For the sake of simplicity and without sacrificing applicability or informative value, the following example is limited to two markets and competitors.

The backward induction begins again with the payment comparisons at the last decision node, which in this example are written to the monopolist . Here, the payouts of the branches that do not contain any special action must be ignored, since the monopolist has no control over them; At this point they are only used for illustration purposes and could just as well be a station beforehand . ${\displaystyle {\begin{aligned}M\end{aligned}}}$ ${\displaystyle {\begin{aligned}K_{2}out\end{aligned}}}$

For the monopolist, the comparison of payments all shows that "tolerating" is strictly better than "fighting":

${\displaystyle {\begin{aligned}u_{M}(D_{M},D_{M};IN_{K1};in_{K2})=4>2=u_{M}(D_{M},B_{M};IN_{K1};in_{K2})\end{aligned}}}$ ... etc.,

For the competitors and that getting in ("IN", or "in") is always strictly better than staying outside ("OUT" or "out"): ${\displaystyle {\begin{aligned}K_{2}\end{aligned}}}$ ${\displaystyle {\begin{aligned}K_{1}\end{aligned}}}$

${\displaystyle {\begin{aligned}u_{K2}(D_{M},D_{M};s_{K1}^{i};in_{K2})=2>1=u_{K2}(D_{M},D_{M};s_{K1}^{i};out_{K2})\end{aligned}}}$

${\displaystyle {\begin{aligned}u_{K1}(D_{M},D_{M};IN_{K1};s_{K2}^{i})=2>1=u_{K1}(D_{M},D_{M};OUT_{K1};s_{K2}^{i})\end{aligned}}}$,

Result

→ The backward induction delivers subgame perfect Nash equilibrium : . However, it is empirically established time and again that monopoly companies want to wage a price war when a competitor enters (“fight”) and thus harm not only the competitor but also themselves. Rarely has this irrational behavior been based on the monopolist's inability to apply backward induction in practice over several periods. Psychological approaches justify it with the preference of insisting on a predominance position; the monopolist does not want to see that it is also better for him to simply tolerate another provider instead of fighting him with a loss of profit. ${\displaystyle {\begin{aligned}t^{\star }=(D_{M},D_{M};IN_{K1};in_{K2})\end{aligned}}}$

The Millipede Game (Centipede Game after Rosenthal 1981)

Game tree of a 4-stage "millipede" game. Players 1 and 2 (labeled above the nodes) can either take the money pot (D, d) or pass it on (R, r).

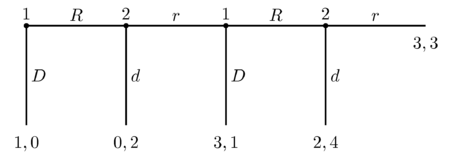
The centipede game is a sequential and finite game in which two players i which alternately have the option to choose a constantly growing pot of money or pass. In the original version by Rosenthal (1981), this game goes over 100 rounds, hence the name "Centipede Game" . But it can be modified to any finite number of rounds that is. The following example should go over a maximum of 4 rounds. The possible actions are: for "row" ( stay in the row ) and for "down" (go down ). ${\displaystyle {\begin{aligned}i\in (1;2)\end{aligned}}}$ ${\displaystyle {\begin{aligned}R\end{aligned}}}$ ${\displaystyle {\begin{aligned}R>1\end{aligned}}}$ ${\displaystyle {\begin{aligned}(R_{1},r_{2})\end{aligned}}}$ ${\displaystyle {\begin{aligned}(D_{1},d_{2})\end{aligned}}}$

procedure

If the money pot is selected, the game is automatically over and the players receive their respective payouts.

If it is passed on, the payouts change as follows:

• ${\displaystyle {\begin{aligned}u_{i}-1\end{aligned}}}$, for the player who passes,

• ${\displaystyle {\begin{aligned}u_{i}+2\end{aligned}}}$, for the player who should make the next decision.

• however, the last payout that can be achieved with "Pass on" is always the same for both players: ${\displaystyle {\begin{aligned}u_{1}=u_{2}\end{aligned}}}$

Starting at the last decision node, the following payout comparisons result by means of backward induction :

Benefits for Player 2: . The last "r branch" can be crossed out. ${\displaystyle {\begin{aligned}u_{2}(s_{1};r_{2},r_{2})=3<4=u_{2}(s_{1};d_{2},d_{2})\end{aligned}}}$

Player 1: . Again an “R branch” is deleted. ${\displaystyle {\begin{aligned}u_{1}(R_{1},R_{1};s_{2})=2<3=u_{1}(D_{1},D_{1};s_{2})\end{aligned}}}$

Player 2: ... etc. ${\displaystyle {\begin{aligned}u_{2}(s_{1};r_{2},r_{2})=1<2=u_{2}(s_{1};d_{2},d_{2})\end{aligned}}}$

Result

→ The “R” action (passing on the pot) is dominated by each player in each round by the “D” action (choosing the money pot himself). The subgame-perfect Nash equilibrium is . So if one does not speculate on mutual and benevolent trust, this game ends immediately in the first round with the acceptance of the money pot. Self-interest or distrust of the other actor prevents the collective more rational choice of “passing on”. If there was an insurance that the other player would cooperate, higher payouts could be realized for both players. Empirical studies show, however, that the immediate choice of "D" or "d" is rarely observed. Usually "R" ("r") is played over several rounds so that the pot increases until someone finally plays "D" ("d"). The realization by playing “always R, r” has been observed just as rarely as “always D, d”. This example shows that the backward induction does not always lead to the Pareto-optimal payout allocation, despite correct application. ${\displaystyle {\begin{aligned}t^{\star }=(D_{1},D_{1};d_{2},d_{2})\end{aligned}}}$

Overarching example

The hangman's paradox

→ Main article : Paradox of the unexpected execution

This mathematical and philosophical paradox is described as follows.

A convicted prisoner is told by his executioner:

1. he is to be hanged at noon on the next weekday (Monday – Friday).
2. it would take place completely unexpectedly for him. (Due to the additional agony of unpredictability, he should not receive any additional information about which of the following five days the execution is to take place.)

He then thinks about the following (solution using a similar procedure as with backward induction ): “If I survive midday on the penultimate day of the week, I will have to be executed on Friday midday, but that would not be unexpected. So the last possible date can be excluded. If I'm still alive at noon before the penultimate appointment (Wednesday), the execution could be scheduled for the last (on Friday) or penultimate appointment (Thursday), but I have already excluded the last one, so only the penultimate one remains; That would not be unexpected, however, as Thursday would be the last possible date. Am I still alive at noon before the penultimate appointment ... "etc.

"... the only possibility would be that I would be hanged on Monday, but since I already know that, this day is no longer surprising for me either!"

Result

The prisoner concludes that he cannot be hanged unexpectedly at all . In the first known versions of this paradox it is even described that he deduces from it that he will probably not be hanged at all . He is making a logical fallacy because, due to the successful falsification of the executioner's / judge's 2nd statement, he assumes that the 1st statement has also been refuted ( cum hoc ergo propter hoc ). He therefore assumes that both assumptions would be correlated, possibly even causal, with one another.

See also

• Game theory
• Solution concept
• Extensive form
• Normal form
• Nash equilibrium
• Partial perfect balance

literature

• R. Gibbons: "A Primer in Game Theory" Harvester Wheatsheaf, London 2001
• H. Wiese: “Decision-making and game theory” Springer, Berlin 2002
• C. Rieck "Game Theory - An Introduction" Rieck, Eschborn 2007
• T. Pries: "Combat price abuse in economized EC antitrust law" Mohr Siebeck, 2009
• MJ Holler, G. Illing: “Introduction to Game Theory”, Springer 6th edition, Berlin, 2005
• S. Berninghaus, KM Ehrhart: Strategic Games: An Introduction to Game Theory , Springer 3rd Edition, Berlin 2010
• A. Diekmann: "Game theory:" Introduction, examples, experiments ", rororo 2nd edition, 2009
• J. Neumann and O. Morgenstern: Theory of Games and Economic Behavior , Princeton University Press, 1944, online at archive.org (PDF; 31.6 MB)
• R. Aumann: "Backward Induction and Common Knowledge of Rationality", Games and Economic Behavior Vol. 8 pages 6-19, 1995
• MJ Osborne, A. Rubinstein: "A Course in Game Theory". MIT Press p. 135, 1994
• R. Selten: "The chain store paradox", Theory and Decision Vol. 9, pp. 127-159, 1978
• R. McKelvey and T. Palfrey: "An experimental study of the centipede game", Econometrica Vol. 60, pages 803-836, 1992
• TY Chow, "The surprise examination or unexpected hanging paradox," The American Mathematical Monthly Jan 1998

Web links

• Wikiludia: Game Theory Encyclopedia
• Game theory script at the University of Munich
• Solving sequential games with backward induction
• Glossary of game theory terms
• Problems with backward induction
• Game theory entry in the business lexicon

Individual evidence

1. ^ J. Neumann and O. Morgenstern: Theory of Games and Economic Behavior , Princeton University Press, 1944.
2. ^ Robert Gibbons: A Primer in Game Theory , First Edition, Financial Times, Harlow, page 95, 1992
3. ^ R. Aumann: "Backward Induction and Common Knowledge of Rationality", Games and Economic Behavior Vol. 8 pages 6-19, 1995 | doi = 10.1016 / S0899-8256 (05) 80015-6
4. ^ MJ Osborne, A. Rubinstein: "A Course in Game Theory". MIT Press, p. 135 1994
5. ↑ D. Borg beams and E. Winter: "A Necessary and sufficient epistemic condition for playing backward induction" Journal of Mathematical Economics., 1995
6. ↑ McKelvey, Richard D., McLennan, Andrew M., and Turocy, Theodore L. (2010). Gambit: Software Tools for Game Theory, Version 0.2010.09.01. http://www.gambit-project.org .
7. ↑ R. Selten: "The chain store paradox", Theory and Decision Vol. 9, pages 127-159, 1978 doi = 10.1007 / BF00131770
8. ↑ T. Pries: “Combat price abuse in economized EC antitrust law”, pages 25-27, Mohr Siebeck, 2009, ISBN 3-16-150166-7
9. ^ R. McKelvey and T. Palfrey: "An experimental study of the centipede game", Econometrica Vol. 60, pages 803-836, 1992.
10. ^ I. Palacios-Huerta and O. Volij "Field Centipedes", American Economic Review, Vol. 99 pp. 1619–1635, 2009.
11. ^ TY Chow, "The surprise examination or unexpected hanging paradox," The American Mathematical Monthly Jan 1998
12. ↑ Eric Weisstein: Unexpected Hanging Paradox . In: MathWorld (English).