Repeated games

Repeated games are a special case of dynamic games in game theory . They are used to represent repeated interactions between actors. In such a game, the players in the same decision-making situation meet in several rounds. The outcome of the game differs significantly from the static games ( one-shot game ), in which the players only interact once. This is due to the fact that future behavior of the players can only be conditioned to their past behavior after repeating the game. Therefore it is possible to “punish” or “reward” each other in the following rounds.

Much of the repetitive game analysis has been driven by Robert Aumann .

Examples of repeated interactions: competition in markets (providers in an oligopoly market ), insurance contracts, auctions , trading within companies or groups (employers and employees, family members).

Structure of repeated games

Repeated interactions are represented as a dynamic game, in which the players play the same static game (level game) every round . If this level game is repeated infinitely often, it is called a super game . Given a static game with complete information, players simultaneously choose a strategy from the set of strategies and receive the payout . The payouts received by players in a round depend only on the actions chosen in that round . The functional relationship remains the same for all individual rounds . Immediately after each round, the strategies of all players can be observed. The course of the game up to time t is referred to as . Decisions in previous rounds thus influence the strategies of the players and the resulting payouts in subsequent rounds. The time preference of the players is represented by a discount factor . The players try their payouts on all rounds of time to maximize: . The closer the discount factor is to one, the more indifferent the players are with regard to the time of the payout. If the discount factor is close to zero, the time preference is very high and the future does not matter. This can be compared to a static (one-shot) game. ${\displaystyle G}$ ${\displaystyle G(\infty )}$ ${\displaystyle G=\lbrace S_{1},\dotsc ,S_{n};\ u_{1},\dotsc ,u_{n}\rbrace }$ ${\displaystyle 1{\text{ bis }}n}$ ${\displaystyle S_{1}{\text{ bis }}S_{n}}$ ${\displaystyle s_{1}{\text{ bis }}s_{n}}$ ${\displaystyle u_{1}(s_{1},\dotsc ,s_{n}){\text{ bis }}u_{n}(s_{1},\dotsc ,s_{n})}$ ${\displaystyle u_{t}\ ({\text{wobei}}\ t=1,\dotsc ,n)}$ ${\displaystyle s_{t}}$ ${\displaystyle u_{t}\ (s_{t})}$ ${\displaystyle h_{t}}$ ${\displaystyle 0\leq \delta \leq 1}$ ${\displaystyle \max \sum \nolimits _{t=0}^{n}\delta ^{t}{u_{i}}_{t}({s_{i}}_{t}(h_{t}))}$ ${\displaystyle \delta }$

Relevant for the outcome of a repeated game is

• whether it is repeated finitely or indefinitely,

• whether the underlying step game has only one Nash equilibrium or several equilibria and

• whether or not withdrawals are discounted.

Final repetition

If a static game, e.g. If, for example, the prisoner's dilemma is repeated several times in a row by the same players with a foreseeable end, one speaks of a game that is finitely repeated. The distinction between unique and multiple Nash equilibria is of great importance for the outcome of the game. This is illustrated below using 2 examples:

Clear Nash equilibrium

Assume that the underlying level game ( prisoner's dilemma ), with the clear Nash equilibrium (D, d), is played twice in a row:

Player 1 / Player 2	Defective (d)	Cooperate (c)
Defect (D)	(1, 1)	(5, 0)
Cooperate (C)	(0, 5)	(4, 4)

In the first round, the players decide at the same time whether they “cooperate” or “fail”. After the end of the first round, the decisions of the players will be announced. The step game is then repeated.

The payout results after the outcome of the second round from the sum of the balance payouts of the individual rounds:

Player 1 / Player 2	Defective (d)	Cooperate (c)
Defect (D)	(2, 2)	(6, 1)
Cooperate (C)	(1, 6)	(5, 5)

2x repeated prisoner's dilemma in extensive form

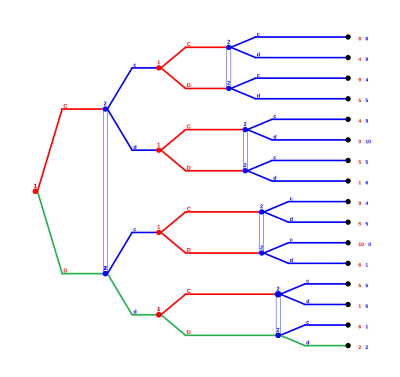
Analysis of the game by backward induction :

This game contains 4 real sub-games , each starting from the second round (see graphic game tree).

2nd round: Regardless of the outcome of the first round, the Nash equilibrium (D, d) is always played in all four sub-games.

1st round: The payout of the second round (1.1) is added to the payout of the first round, as the decision of the first round has no influence on the outcome of the game.

The only Nash equilibrium arises when both players fail every round. Therefore, there should be no cooperation in the first round either. This results from the fact that deviant behavior cannot be sanctioned in the second round. In a 2x2 prisoner's dilemma, cooperation cannot be achieved from a rational point of view.

Definition ( Reinhard Selten 1965): A Nash equilibrium is subgame perfect if the strategies of the players in each subgame form a Nash equilibrium.

The only subgame perfect equilibrium (green) arises when both players "fail" in each round:

Strategy column 1: (D1, D2D2D2D2),

Strategy column 2: (d1, d2d2d2d2),

where (D1, d1) denotes the strategy combination of the 1st round and (D2D2D2D2, d2d2d2d2) the strategy combination for each part of the 2nd round.

Result: If the level game has a clear Nash equilibrium, then the repeated game G (T), for T finite, has a clear subgame-perfect equilibrium, namely the repetition of the Nash equilibrium of the level game in every round.

Multiple Nash equilibria

The original prisoner's dilemma is expanded to include an additional strategy, which creates a further Nash equilibrium. Assume that the level game (extended prisoner's dilemma) with two pure Nash equilibria (D, d) and (E, e) is played twice in a row:

Player 1 / Player 2	Defective (d)	Cooperate (c)	Additional strategy (s)
Defect (D)	(1, 1)	(5, 0)	(0, 0)
Cooperate (C)	(0, 5)	(4, 4)	(0, 0)
Additional strategy (E)	(0, 0)	(0, 0)	(3, 3)

In the first round, the players determine their strategy at the same time. Afterwards the decisions of the players will be announced. The step game is then repeated. Part-game perfection also exists in the extended game G (2) if the Nash equilibrium (D, d) is chosen in every round regardless of the course of the game (see unambiguous equilibrium). However, there are other subgame-perfect equilibria in G (2), which can be determined with the help of backward induction:

2nd round : Regardless of the outcome of the first round, a Nash equilibrium is always played in all nine sub-games. Since there are two equilibria in this game, one of which gives a higher payout (E, e) and one a lower payout (D, d), the decision of the first round can be sanctioned or rewarded in this round.

1st round : In the first round, the players anticipate that a Nash equilibrium of the partial game will be played in the 2nd round. Since there are two Nash equilibria, it is possible for the players to influence the outcome of the game through the choice of strategy in this round. This depends on the discount factor . The closer the value is to 1, the more likely the players will cooperate, as payouts are weighted higher in subsequent rounds. For against 0, the situation is exactly the opposite. ${\displaystyle 0\leq \delta \leq 1}$ ${\displaystyle \delta }$

Cooperation is made possible here, based on a credible threat, to play the "worse" Nash equilibrium (D, d) in the second round, if the first round deviates. A deviation from the strategy (C, c) brings a higher payout for the deviating player in the 1st round, but a lower one overall: (C, c) + (E, e) = (7.7) for cooperation and (D, c) + (D, d) = (6.1) or (C, d) + (D, d) = (1.6) for one-sided deviation. Even if the additional strategy (E, e) is played in both rounds, the payout is lower (6.6) <(7.7).

Result: In a finitely repeated game with several Nash equilibria, equilibria can exist in which strategies are chosen that do not form Nash equilibria in the level game, such as the Pareto-optimal strategy combination (C, c).

Infinite repetition

In contrast to finitely frequent repetitions, it can be profitable to cooperate with your opponent in games that are repeated infinitely or indefinitely. Each player maximizes the present value of his discounted payouts with an infinite time horizon . An analysis of the game with the help of backward induction is no longer possible due to the lack of a definitive final round. Analyzing the resulting game completely is very time-consuming because of the large number of possible strategies. Therefore one has to limit oneself to the formulation of a few explicit strategies. ${\displaystyle 0\leq \delta \leq 1}$

Trigger strategy

Trigger strategies are the most popular strategy in infinite games. They are characterized by the following features:

1. The game begins with mutual cooperation.
2. There is cooperation until at least one of the players is defective.
3. This results in defection as a punishment in the following rounds.

In addition to the selection of a strategy, the reputation of the player is relevant for the outcome of the game . Through repeated interaction it is possible to cooperate and achieve a Pareto-optimal state. stands for the payout if the agreed strategy is played in a round . stands for the payout if all players stick to the agreed strategy for t rounds . However, if one of the two players deviates from the cooperation because a one-sided defect can bring a higher payout in the short term , there is no longer any cooperation in the following rounds and consequently only a payout of is achieved, whereby stands for the strategy in which the Nash equilibrium of the level game is played becomes. In an infinite game, a long-term view is important. The players discount their payout with a factor . In the event that the discounted value of future round winnings with cooperation exceeds the value of the one-time deviation and then continuous defection, the player will cooperate with rational behavior. Consequently, it can make sense for the players to refrain from a higher profit in the short term in order to achieve higher payouts in the long term. ${\displaystyle u_{i}(s^{*})}$ ${\displaystyle s^{*}}$ ${\displaystyle u_{i}(\sigma ^{*})}$ ${\displaystyle s^{*}}$ ${\displaystyle u_{i}(r_{i}(s^{*}))}$ ${\displaystyle u_{i}(s^{c})}$ ${\displaystyle s^{c}}$ ${\displaystyle 0\leqq \delta \leqq 1}$

Payout if all players adhere to the agreements:

${\displaystyle u_{i}(\sigma ^{*})=u_{i}(s^{*})[1+\delta _{i}+\delta _{i}^{2}+\dotsc ]=u_{i}(s^{*})\sum \nolimits _{t=0}^{\infty }\delta _{i}^{t}={\dfrac {u_{i}(s^{*})}{(1-\delta _{i})}}}$

Payment for the deviator:

${\displaystyle u_{i}(r_{i}(s^{*}))+u_{i}(s^{c}){\dfrac {\delta _{i}}{1-\delta _{i}}}}$

A deviation on is therefore not advantageous if: ${\displaystyle r_{i}(s^{*})}$

${\displaystyle {\begin{aligned}u_{i}(r_{i}(s^{*}))+u_{i}(s^{c}){\dfrac {\delta _{i}}{1-\delta _{i}}}&<{\dfrac {u_{i}(s^{*})}{1-\delta _{i}}}\\u_{i}(r_{i}(s^{*}))+u_{i}(s^{*})&<[u_{i}(s^{*})-u_{i}(s^{c})]{\dfrac {\delta _{i}}{1-\delta _{i}}}\\\delta _{i}&>{\dfrac {u_{i}(r_{i}(s^{*}))-u_{i}(s^{*})}{u_{i}(r_{i}(s^{*}))-u_{i}(s^{c})}}\\\end{aligned}}}$

There are, among other things, the following modifications of the trigger strategies:

• Grim trigger is the harshest form of sanction for uncooperative behavior, since a one-time deviation results in defects until the end of the game.

	Train 1	Move 2	Train 3	Move 4	Move 5	Move 6	Move 7	Train 8	...
Player A	C.	C.	C.	D.	D.	D.	D.	D.
Grim player	C.	C.	C.	C.	D.	D.	D.	D.

• Tit for Tat (Like you me, like me you) is a weakened form of the trigger strategy. The previous strategy of the opponent is imitated in the current round. The game starts with cooperative behavior until one of the players deviates. In contrast to Grim-Trigger, cooperation can be achieved again in the event of a one-off deviation:

	Train 1	Move 2	Train 3	Move 4	Move 5	Move 6	Move 7	Train 8	...
Player A	C.	C.	D.	C.	C.	D.	D.	C.
TfT player	C.	C.	C.	D.	C.	C.	D.	D.

Evidence through experiments (Axelrod)

In order to determine successful strategies in an infinitely repeated prisoner's dilemma, Robert Axelrod developed a computer program in which different strategies competed against each other. The result of the experiment: over the entire course of the game, the tit-for-tat strategy achieves the best result, although it is inferior to other strategies in individual comparison. Reasons for this are:

1. Friendliness (nice): It always starts with cooperation and defects do not come about if no one deviates from the cooperation.
2. Retaliation (retaliatory): Continuous defection brings no advantage, since mutual defection is continued.
3. Forgiveness: As soon as one of the players cooperates again, the second player follows suit. Errors are thus "forgiven".
4. Simplicity of the strategy: It is very easily recognized by players, which is why long-term cooperation can be made possible.

Conclusion : Tit for Tat combines the characteristics that on the one hand friendliness pays off through long-term cooperation and on the other hand deviant behavior can be sanctioned. It does best at infinite iterations of the Prisoner's Dilemma as it maximizes the total payout for players.

example

In an infinitely repeated game, players discount their payout by the factor where . This factor can also be interpreted as a continuation probability, since the players do not know whether the game will be continued with certainty or not. The following assumptions should apply to the present example: It is uncertain whether another round of the repeated game will follow. The probability that a round will be followed by another round is . Therefore, the probability that the game will end after the current round is 1- . The probability that the game will still be played in round t is the same . If is sufficiently large, there is a subgame-perfect equilibrium in the infinitely often repeated prisoner's dilemma, in which both players cooperate along the equilibrium path in all rounds. ${\displaystyle \delta }$ ${\displaystyle 0\leq \delta \leq 1}$ ${\displaystyle \delta }$ ${\displaystyle \delta }$ ${\displaystyle \delta ^{t}}$ ${\displaystyle \delta }$

Player 1 / Player 2	Defective (d)	Cooperate (c)
Defect (D)	(1, 1)	(5, 0)
Cooperate (C)	(0, 5)	(4, 4)

With the given assumptions one can investigate a certain dynamic strategy. With the Grim-Trigger strategy, you cooperate until the opponent is defective, and then defective in turn in every round. If both players use Grim Trigger, they cooperate in each round and the players receive a payout of 4.

The payout behaves differently if a player does not comply with the cooperation and is defective from round N. It follows from this that the player cooperates with the Grim strategy up to round N and only defects in the following rounds. In the first N-1 rounds the player who refuses to cooperate from round N receives a payout of 4. In round N he receives 5 and in the following rounds only a payout of 1.

In order to determine whether it is profitable to deviate from the cooperation with a Grim player, one has to compare the payouts of with each other. denotes the expected value of the payout in the event of a deviation and the expected value of the payout in the event of infinite cooperation. ${\displaystyle \operatorname {E} [\pi (D_{N},Grim)]\ {\text{und}}\ \operatorname {E} [\pi (C,C)]}$ ${\displaystyle \operatorname {E} [\pi (D_{N},Grim)]}$ ${\displaystyle \operatorname {E} [\pi (C,C)]}$

It is worth deviating if:

${\displaystyle {\begin{aligned}\operatorname {E} [\pi (D_{N},Grim)]&\geqq \operatorname {E} [\pi (C,C)]\\5+\sum \nolimits _{t=1}^{\infty }\delta ^{t}*1&\geqq \sum \nolimits _{t=0}^{\infty }\delta ^{t}*4\\\end{aligned}}}$

The first part can be simplified with the help of the limit theorems for infinite geometric series:

• ${\displaystyle {\begin{aligned}\sum \nolimits _{t=0}^{\infty }\delta ^{t}={\dfrac {1}{1-\delta }}\qquad {\text{für}}\left|\delta \right|<1\\\end{aligned}}}$

• ${\displaystyle \sum \nolimits _{t=1}^{\infty }\delta ^{t}={\dfrac {\delta }{1-\delta }}\qquad {\text{für}}\left|\delta \right|<1\,}$

So that for the present prisoner's dilemma results:

${\displaystyle {\begin{aligned}5+{\dfrac {\delta }{1-\delta }}&\geqq {\dfrac {4}{1-\delta }}\\5\cdot (1-\delta )+\delta &\geqq 4\\1&\geqq 4\cdot \delta \\{\dfrac {1}{4}}&\geqq \delta \\\end{aligned}}}$

Cooperation is only profitable if the current round is followed by another with a sufficiently high degree of probability. In this example of the prisoner's dilemma that is repeated indefinitely, the critical point is * = 1/4. In the long run, a higher payout can be expected through cooperation than with defection, if * is greater than 1/4. For , cooperation forms a subgame-perfect Nash equilibrium. ${\displaystyle \delta }$ ${\displaystyle \delta }$ ${\displaystyle \delta \geq {\dfrac {1}{4}}}$

Folk theorem

Payouts achievable through mixed strategies in the Prisoner's Dilemma

→ Main article : Folk theorem

Using the previous example (prisoner's dilemma)

Player 1 / Player 2	Defective (d)	Cooperate (c)
Defect (D)	(1, 1)	(5, 0)
Cooperate (C)	(0, 5)	(4, 4)

the achievable payout vector can be graphically illustrated (see graphic). With infinite repetition of this prisoner's dilemma it is possible to achieve subgame-perfect equilibria that deviate from the static Nash equilibrium (D, d) and result in a higher payout in the long term (if the discount factor is close enough to 1).

This finding is recorded in the so-called folk theorem (generally known "story"), which states that every achievable and individually rational payout vector of a level game can form a subgame-perfect equilibrium payout in the infinitely often repeated game , if the discount factor is close enough to 1. Accessibility and individual rationality are both necessary and (almost always) sufficient conditions for the payout vector to represent an equilibrium payout. ${\displaystyle G(\infty )}$ ${\displaystyle \delta }$

One deviation principle

The 'one deviation' principle serves to simplify the identification of subgame-perfect Nash equilibria in both finitely and infinitely repeated games.

Theorem: A strategy in a finitely or infinitely repeated game is subgame-perfect if and only if there is no strategy that is identical except for a decision and results in a higher payout if this level is reached. ${\displaystyle s_{t}}$ ${\displaystyle s'_{t}}$ ${\displaystyle s_{t}}$

Result: A strategy profile of a repeated game is only then a subgame-perfect Nash equilibrium if it fulfills the one-deviation property.

See also

• Game theory
• Reputation (game theory)
• Folk theorem
• Prisoner's Dilemma
• Nash equilibrium
• The evolution of cooperation

literature

• Drew Fudenberg, David Levine: Subgame-perfect equilibria of finite and infinite-horizon games . Journal of Economic Theory, Volume 31, Issue 2, December 1983, pages 251-268.
• Drew Fudenberg, Jean Tirole: Game Theory . The MIT Press, Cambridge, Massachusetts 1991.
• Dilip Abreu, Prajit K. Dutta and Lones Smith: The Folk Theorem for Repeated Games: A Neu Condition , Econometrica, Vol. 62, No. July 4, 1994.
• Ebbe Hendon, Hans Jørgen Jacobsen, Birgitte Sloth: The One-Shot-Deviation Principle for Sequential Rationality . Games and Economic Behavior, Volume 12, Issue 2, February 1996, pages 274-282.
• Gernot Sieg: Game Theory , 3rd edition, Oldenbourg, Munich 2010.
• Joachim Zentes: Cooperation, Alliances and Networks: Basics - Approaches - Perspectives , 2nd edition, Gabler, Wiesbaden 2005
• Manfred J. Holler, Gerhard Illing: Introduction to Game Theory , 7th edition, Springer, Berlin 2009.
• Robert Axelrod and William D. Hamilton: The Evolution of Cooperation , Science, Vol. 211, March 27, 1981.
• Robert Gibbons: A Primer in Game Theory , First Edition, Financial Times, Harlow 1992.
• Sergiu Hart: Robert Aumann's Game and Economic Theory , Scandinavian Journal of Economics, Vol. 108 (2), March 2006, pages 185-211
• Siegfried Berninghaus, Siegfried K. Berninghaus, Karl-Martin Ehrhart: Strategic Games: An Introduction to Game Theory , 3rd edition, Springer, Berlin 2010.
• Sylvain Sorin: Repeated Games with Incomplete Information. Robert J. Aumann and Michael B. Maschler, with the collaboration of Richard E. Stearns . Games and Economic Behavior, Volume 16, Issue 2, Oct. 1996, pp. 347-352.
• Thomas Riechmann: Game Theory . 3rd edition, Vahlen, Munich 2010.

Web links

• Gametheory.net
• Spieltheorie-Software.de ( Memento from July 18, 2013 in the Internet Archive )
• Iterated Prisoner's Dilemma Game and Simulation

Individual evidence

1. ^ ^{A b c} Robert Gibbons: A Primer in Game Theory , First Edition, Financial Times, Harlow 1992, p. 82
2. ↑ Thomas Riechmann: Game Theory , 3rd Edition, Vahlen, Munich 2010, page 141
3. ^ Sergiu Hart: Robert Aumann's Game and Economic Theory , Scand. J. of Economics 108 (2), Israel 2006, p. 185
4. ^ Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, 145
5. ↑ Manfred J. Holler, Gerhard Illing: Introduction to the game theory , 7th edition, Springer, Berlin 2009, pages 129-132. ISBN 978-3-540-69372-7 .
6. ^ Siegfried Berninghaus, Siegfried K Berninghaus, Karl-Martin Ehrhart: Strategic Games: An Introduction to Game Theory , 3rd edition, Springer, Berlin 2010, page 348.
7. ^ Gernot Sieg: Game Theory , 3rd Edition, Oldenbourg, Munich 2010, page 56
8. ^ Robert Gibbons: A Primer in Game Theory , First Edition, Financial Times, Harlow 1992, p. 95. ISBN 978-0-745-01159-2 .
9. ^ Robert Gibbons: A Primer in Game Theory, First Edition, Financial Times, Harlow 1992, 84
10. ^ Robert Gibbons: A Primer in Game Theory , First Edition, Financial Times, Harlow 1992, pp. 84-88.
11. ↑ ^{a b} Thomas Riechmann: Game Theory , 3rd Edition, Vahlen, Munich 2010, pp. 146–148.
12. ^ ^{A b} Joachim Zentes: Cooperation, Alliances and Networks: Basics - Approaches - Perspectives . 2nd edition, Gabler, Wiesbaden 2005, page 129. ISBN 978-3-409-21985-3 .
13. ^ ^{A b} Joachim Zentes: Cooperation, Alliances and Networks: Basics - Approaches - Perspectives . 2nd edition, Gabler, Wiesbaden 2005, page 130.
14. ↑ Gernot Sieg: Game Theory . 3rd edition, Oldenbourg, Munich 2010, page 57 ff.
15. ↑ Thomas Riechmann: Game Theory , 3rd Edition, Vahlen, Munich 2010, pp. 153–155.
16. ↑ Dilip Abreu, Prajit K. Dutta and Lones Smith: The Folk Theorem for Repeated Games: A New Condition . Econometrica, Vol. 62, No. 4 (July 1994), p. 939.
17. ^ Drew Fudenberg, Jean Tirole: Game Theory . The MIT Press, Cambridge, Massachusetts 1991, p. 109.
18. ↑ Ebbe Hendon, Hans Jørgen Jacobsen, Birgitte Sloth: The One-Shot-Deviation Principle for Sequential Rationality . Games and Economic Behavior, Volume 12, Issue 2, February 1996, pages 274-282.