Negotiated solution

The negotiation solution is a game-theoretic concept for solving cooperative games . A game is called cooperative if the actors can achieve additional profit compared to the situation in which everyone is playing for themselves through a coordinated approach, ie through a common choice of a strategy. In this case, the division of the additional profit has to be negotiated, hence the term bargaining solution. This article is limited to so-called two-person games, i.e. games in which only two players are involved.

The non-cooperative situation

Most parlor games require frequent strategic decisions by the players involved in order to bring about a favorable outcome for them. If you make these decisions for all conceivable game situations before the game starts, you only have to deal with one strategy per player. The execution of the game then only consists in following the decisions already made. This is the mathematician's point of view:

A non-cooperative two-person game consists of two sets and and two figures , one writes briefly . The game consists of each player choosing one element from his set of strategies independently of the other . The i-th player then receives the payout . ${\displaystyle \Gamma }$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle a_{i}\colon S_{1}\times S_{2}\rightarrow {\mathbb {R} }}$ ${\displaystyle \Gamma =(S_{1},S_{2},(a_{1},a_{2}))}$ ${\displaystyle s_{i}}$ ${\displaystyle S_{i}}$ ${\displaystyle a_{i}(s_{1},s_{2})}$

If the strategy sets are finite, they can be numbered and roughly set. The payoff functions are then given by two matrices and one speaks of a bimatrix game. ${\displaystyle S_{1}=\{1,\ldots ,m\},S_{2}=\{1,\ldots ,n\}}$ ${\displaystyle (a_{i}(j,k))_{j=1\ldots m,k=1\ldots n}}$

Each player can guarantee himself a certain payout amount by choosing the best strategy based on the most unfavorable strategy chosen by the opponent

• Player 1: ${\displaystyle \sup _{s_{1}\in S_{1}}\inf _{s_{2}\in S_{2}}a_{1}(s_{1},s_{2})}$
• Player 2: . ${\displaystyle \sup _{s_{2}\in S_{2}}\inf _{s_{1}\in S_{1}}a_{2}(s_{1},s_{2})}$

These are the so-called guaranteed values ​​of the players. If the supremum and infimum are not accepted, one still has approximate guarantees.

A Nash equilibrium is understood as a pair of strategies , so that a player can at most deteriorate by deviating from his strategy one-sided. In the theory of non-cooperative games, in which a common, agreed deviation is not provided, an equilibrium can be understood as the solution to the game. ${\displaystyle (s_{1},s_{2})}$ ${\displaystyle S_{1}\times S_{2}}$

The Prisoner's Dilemma

Probably the best-known game theory situation that virtually challenges the concept of negotiation is the prisoner's dilemma . Two prisoners are charged with a collective crime based on dubious evidence. Everyone has two strategies to choose from: 1 = deny, 2 = confess. If both are denied, only a one-year prison sentence can be imposed, for example for illegal possession of weapons and disturbance of the peace. If both confess, 8 years are due each. If different strategies come together, the confessing person goes unpunished as a key witness, while the denier is faced with 10 years imprisonment. If you take the negative of the years of imprisonment to be served as the payout in this bimatrix game, then applies to the payout matrices

${\displaystyle a_{1}={\begin{pmatrix}-1&-10\\0&-8\end{pmatrix}},\,\,a_{2}={\begin{pmatrix}-1&0\\-10&-8\end{pmatrix}}}$

The only point of equilibrium is evidently (2,2), i.e. H. both prisoners confess. (1,1) is not an equilibrium, as each player can secure himself impunity by changing strategies at the expense of the other. Since everyone involved knows this, the strategy combination (1,1) even appears very unstable.

Nevertheless, (1,1) is certainly the optimal solution from the delinquent's point of view . But for this they would have to be able to make an agreement, i. H. Negotiate the strategies to be used. This is modeled by the concept of cooperation.

cooperation

In order to be able to model negotiations mathematically, we extend the definition of the non-cooperative game to with and . We call K the set of cooperative strategies. If a cooperative strategy k is selected, the i-th player receives the payout . Since each player can also play his own strategy, but this may be an arrangement with the other player who is no longer seen as an opponent. ${\displaystyle \Gamma =(S_{1},S_{2},(a_{1},a_{2}))}$ ${\displaystyle \Gamma =(S_{1},S_{2},K,(a_{1},a_{2}))}$ ${\displaystyle K\supseteq S_{1}\times S_{2}}$ ${\displaystyle a_{i}\colon K\rightarrow {\mathbb {R} }}$ ${\displaystyle a_{i}(k)}$ ${\displaystyle K\supseteq S_{1}\times S_{2}}$

We can model the prisoner's dilemma with , it then only depends on the possibility of agreement. If one looks at two economic actors who have their own production strategies for the same market in the non-cooperative situation, then cooperative strategies are quite conceivable that go beyond an agreement on the production strategies, e.g. B. the establishment of a cartel or the coordination of production by connecting different processing stages in series. What is permitted as a cooperative strategy is part of the rules of the game, the cartel law is one of those rules. ${\displaystyle K=S_{1}\times S_{2}}$

Negotiation situations

Negotiation situation ${\displaystyle (B,d)}$

Let us now focus on the accompanying picture of a common payoff function in , d. H. we abstract from the strategies that lead to these payouts. contains a point that consists of payouts that each player can secure himself, e.g. B. the above-defined guaranteed values (also called initial equipment or threat point ). The players will certainly only negotiate about payouts where and is, otherwise a player would be better off with his guaranteed value. Furthermore, there should be a possible payout with and so that there is something to negotiate for both players (existence of a negotiation incentive ). ${\displaystyle (a_{1},a_{2})}$ ${\displaystyle {\mathbb {R} }^{2}}$ ${\displaystyle B=(a_{1},a_{2})(K)\subset {\mathbb {R} }^{2}}$ ${\displaystyle B}$ ${\displaystyle d=(d_{1},d_{2})}$ ${\displaystyle x=(x_{1},x_{2})}$ ${\displaystyle d_{1}\leq x_{1}}$ ${\displaystyle d_{2}\leq x_{2}}$ ${\displaystyle x=(x_{1},x_{2})}$ ${\displaystyle d_{1}<x_{1}}$ ${\displaystyle d_{2}<x_{2}}$

In addition, we allow players a joint probability distribution on to choose. The payout point is then calculated as the expected value : ${\displaystyle \mu }$ ${\displaystyle K}$

${\displaystyle \int _{K}(a_{1}(k),a_{2}(k))\,d\mu (k).}$

We can therefore assume the number of possible payout points to be convex , because by choosing together the players can realize any convex combination of payout points. Furthermore, we can assume that is limited by excluding unlimited withdrawal functions as unrealistic. Let us also assume that it is closed , is even compact . This motivates the following conceptual formation, which goes back to Ehud Kalai and Meir Smorodinsky : ${\displaystyle B}$ ${\displaystyle \mu }$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle B}$

A negotiation situation is a couple with the following characteristics: ${\displaystyle (B,d)}$

• ${\displaystyle B\subset {\mathbb {R} }^{2}}$ convex and compact,
• ${\displaystyle d\in B}$,
• applies to all components , ${\displaystyle x\in B}$ ${\displaystyle d\leq x}$
• there is a with and . ${\displaystyle (x_{1},x_{2})\in B}$ ${\displaystyle d_{1}<x_{1}}$ ${\displaystyle d_{2}<x_{2}}$

The negotiation problem

If there is a negotiation situation, the choice of a payout point is called a negotiation result. The i-th player receives the payout . The negotiation problem is to find such a negotiation result in every negotiation situation. If the set of all negotiation situations, we therefore define: ${\displaystyle (B,d)}$ ${\displaystyle x=(x_{1},x_{2})\in B}$ ${\displaystyle x_{i}}$ ${\displaystyle {\mathcal {B}}}$

A negotiated solution is a feature with for everyone . ${\displaystyle \varphi \colon {\mathcal {B}}\rightarrow {\mathbb {R} }^{2}}$ ${\displaystyle \varphi (B,d)\in B}$ ${\displaystyle (B,d)\in {\mathcal {B}}}$

Properties of negotiated solutions

Of course, certain characteristics will be required of a negotiated solution that make the solution appear “reasonable”. The negotiated solution is certainly not very “sensible” for everyone , since no player receives more from the negotiation than he could secure himself anyway. The aim in the following is therefore to find meaningful properties with the aim of defining a clear payout point in every negotiation situation. ${\displaystyle \varphi (B,d):=d}$ ${\displaystyle (B,d)\in {\mathcal {B}}}$

Pareto optimality

A Pareto-optimal negotiation result

A negotiated solution is called Pareto-optimal if there is no one with a component for any negotiation situation. I.e. A negotiated solution is always found that does not allow both parties to be better off at the same time. ${\displaystyle \varphi \colon {\mathcal {B}}\rightarrow {\mathbb {R} }^{2}}$ ${\displaystyle (B,d)\in {\mathcal {B}}}$ ${\displaystyle x\in B}$ ${\displaystyle \varphi (B,d)<x}$

This condition is mathematically obvious. In practice it may be difficult to find such negotiated solutions that are not in need of improvement.

symmetry

A symmetrical negotiation result

A negotiated solution is called symmetrical if the following applies: If the negotiation situation is symmetrical, that is, and is also for everyone , then the components of the negotiation result also match. ${\displaystyle \varphi }$ ${\displaystyle (B,d)}$ ${\displaystyle d_{1}=d_{2}}$ ${\displaystyle (x_{1},x_{2})\in B}$ ${\displaystyle (x_{2},x_{1})\in B}$ ${\displaystyle \varphi (B,d)}$

This requires that the negotiated solution does not change in a perfectly symmetrical situation when the players switch roles. Both players are assumed to have the same negotiating skills.

Independence from positive linear transformations

We consider positive linear transformations with . For both components, T means a change in the scale along with a shift. A negotiated solution is called independent of positive linear transformations if for every positive linear transformation T and every negotiation situation that . ${\displaystyle T\colon {\mathbb {R} }^{2}\rightarrow {\mathbb {R} }^{2},\,T(x_{1},x_{2})=(a_{1}x_{1}+b_{1},a_{2}x_{2}+b_{2})}$ ${\displaystyle a_{1}>0,a_{2}>0}$ ${\displaystyle \varphi \colon {\mathcal {B}}\rightarrow {\mathbb {R} }^{2}}$ ${\displaystyle (B,d)}$ ${\displaystyle T(\varphi (B,d))=\varphi (T(B),T(d))}$

The requirement for independence from positive linear transformations is mathematically very obvious and also indispensable for many mathematical considerations. In practice this means that the negotiations take place regardless of the size of the negotiating pool. Since negotiations cost time and resources, one can doubt whether this requirement is relevant in practice.

Independence from irrelevant alternatives

The points out are irrelevant alternatives ${\displaystyle {\tilde {B}}\setminus B}$

A negotiated solution is independent of irrelevant alternatives if for two negotiation situations with always applies. ${\displaystyle \varphi \colon {\mathcal {B}}\rightarrow {\mathbb {R} }^{2}}$ ${\displaystyle (B,d),({\tilde {B}},d)}$ ${\displaystyle \varphi ({\tilde {B}},d)\in B\subset {\tilde {B}}}$ ${\displaystyle \varphi ({\tilde {B}},d)=\varphi (B,d)}$

This requirement seems obvious, as it says that a solution found in the larger negotiation set , which is already in the smaller negotiation set B, will also be the solution for the smaller negotiation set, because even in the larger negotiation set you can't find anything better. Only psychological objections can be raised against this demand: A changed negotiation situation changes the negotiation behavior. ${\displaystyle {\tilde {B}}}$

monotony

The situation improves for both players in the larger number of negotiations.

For a negotiation situation is the maximum payout that would be possible for the i-th player. A negotiated solution is called monotonic if for with for i = 1,2 and always follows component-wise . ${\displaystyle (B,d)}$ ${\displaystyle m_{i}(B):=\sup\{x_{i};(x_{1},x_{2})\in B\}}$ ${\displaystyle \varphi \colon {\mathcal {B}}\rightarrow {\mathbb {R} }^{2}}$ ${\displaystyle (B,0),({\tilde {B}},0)\in {\mathcal {B}}}$ ${\displaystyle m_{i}(B)=m_{i}({\tilde {B}})=1}$ ${\displaystyle B\subset {\tilde {B}}}$ ${\displaystyle \varphi (B,0)\leq \varphi ({\tilde {B}},0)}$

So if both players can only secure the amount 0 and both can achieve a maximum payout of 1, there should be no deterioration for either player if one changes from a smaller negotiated amount to a larger one while maintaining these conditions.

Existence and uniqueness theorems

Nash's negotiated solution

→ Main article : Nash solution

Nash's theorem: There is exactly one Pareto-optimal, symmetrical negotiation solution that is independent of positive linear transformations and independent of irrelevant alternatives.

If two players accept the four requirements for a negotiated solution mentioned here, then there is a clear negotiated solution in every negotiation situation, this is called the Nash negotiation solution. This negotiated solution can be determined as follows: If a negotiated situation , the function assumes the maximum in exactly one point from B, and this point is Nash's negotiated solution. ${\displaystyle (B,d)}$ ${\displaystyle f\colon B\rightarrow {\mathbb {R} },\,f(x_{1},x_{2})=(x_{1}-d_{1})\cdot (x_{2}-d_{2})}$

Nash's negotiated solution is not monotonous!

The monotonous negotiated solution

→ Main article : Kalai-Smorodinsky solution

Kalai-Smorodinsky theorem: There is exactly one Pareto-optimal, symmetrical, monotonous negotiation solution that is independent of positive linear transformations.

This solution is called the monotonous negotiated solution. To determine the monotonous negotiation solution, a positive linear transformation T is determined for a given negotiation situation, so that and . On the straight line there is a point that is largest in terms of component order . The negotiation result sought is then . ${\displaystyle (B,d)}$ ${\displaystyle T(d)=0}$ ${\displaystyle m_{1}(T(B))=m_{2}(T(B))=1}$ ${\displaystyle \{(x,x);x\in {\mathbb {R} }\}}$ ${\displaystyle (x^{*},x^{*})\in T(B)}$ ${\displaystyle T^{-1}(x^{*},x^{*})}$

Negotiated solution to the prisoner's dilemma

Only the gray-shaded area is negotiated.

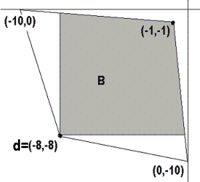
In the situation of the prisoner's dilemma , the set of possible joint payouts with the above numbers consists of the four points (-8, -8), (0, -10), (-10.0) and (-1, -1) . The convex hull is the rectangle created by these points. The guarantee point is d = (- 8, -8). There is nothing to negotiate about non-gray-shaded points in the adjacent drawing, so the gray-shaded area is the negotiation set B. Both solution concepts, the Nashian and the monotonous negotiation solution, list (-1, -1) as the solution.

Final remarks

• One often reads about the requirement of individual rationality, according to which the negotiation result must always be component wise not worse than the guarantee point. In the presentation given here, this requirement is already contained in the definition of the negotiation situation.
• As to monotony, one could have asked more generally that in every negotiation situation the situation for both players can only be improved if the negotiation set B is increased under otherwise identical conditions. It turns out that this demand is so strong that it no longer allows a negotiated solution.
• In the case of the monotonous negotiated solution, compared to the Nash's negotiated solution, only the independence of irrelevant alternatives has been replaced by the monotony requirement.
• The Nashian and the monotonous negotiation solution agree in symmetrical negotiation situations, such as B. in the prisoner's dilemma.
• When formulating his moral philosophy , the Canadian-American philosopher David Gauthier designed an independent variant of the negotiation game, which is characterized by the fact that the two rational actors get closer and closer through concessions and therefore negotiate until the maximum of these relative concessions is minimal ( minimax -Principle of relative concessions ). A rational player - according to Gauthier - would prima facie not be willing to agree to a negotiation result in which the degree of his relative concessions is higher than that of the other player. In general, the Gauthier solution differs from the Nash solution. For games with symmetrical negotiation rooms, however, the solutions coincide, because both parties then receive the same payouts. For Gauthier, this aspect gives rise to the claim that his rational solution is at the same time the moral solution. So he argues for the plausibility of his proposal with recourse to his view of the concessions: The actor who contributes more to the cooperative agreement should be entitled to a correspondingly larger share of the profit from the cooperation. To accept this is rational. Moral restrictions are consequently as impartial factors ( "impartiality" in so far as legitimate) than they are for the totality of all parties ultimately more advantageous to meet the individual needs. Morality and (enlightened) rationality coincide in this theoretical approach.

See also

• Rubinstein negotiation model
• Bargaining power
• Bargaining theory by Komorita and Chertkoff

literature

• John Forbes Nash Jr .: The bargaining problem. In: Econometrica. 18, 1950, ISSN  0012-9682 , pp. 155-162.
• Ehud Kalai , Meir Smorodinsky: Other solutions to Nash's bargaining problem. In: Econometrica. 43, 1975, pp. 513-518.
• Ehud Kalai: Proportional Solutions to Bargaining Situations. Interpersonal utility comparisons. In: Econometrica. 45, 1977, pp. 1623-1630.
• Burkhard Rauhut , Norbert Schmitz , Ernst-Wilhelm Zachow: Game theory. An introduction to the mathematical theory of strategic games. With 50 exercises and numerous examples. Teubner, Stuttgart 1979, ISBN 3-519-02351-2 ( guidelines for applied mathematics and mechanics 49, Teubner study books - mathematics ).
• Manfred J. Holler, Gerhard Illing: Introduction to game theory. 3rd improved and enlarged edition. Springer, Berlin et al. 1996, ISBN 3-540-61017-0 ( Springer textbook ).
• Avinash K. Dixit , Barry J. Nalebuff: Game Theory for Beginners. Strategic know-how for winners. Schäffer-Poeschel, Stuttgart 1997, ISBN 3-7910-1239-8 .
• David Gauthier : Morals By Agreement. Oxford University Press, Oxford 1999, ISBN 978-0198249924 .