Inequality
An inequality is a subject in mathematics that can be used to formulate and study size comparisons . Any inequality consists of two terms , which by one of the reference character <( less-than sign ) ≤ (Kleiner equal sign) ≥ (Greater than or equal sign) or> ( greater-than sign ) are connected.
If and are two terms, then is an inequality. One speaks " smaller (than) ". As with an equation , the left side and the right side of the inequality are called.
The values appearing in the two terms are mostly real numbers . The order relation referred to by the comparison symbol then relates to the natural arrangement of the real numbers.
Forms of inequalities
The following five forms of inequalities are possible:
- (1) ( smaller )
- (2) ( less than or equal to )
- (3) ( larger )
- (4) ( greater than or equal to )
- (5) ( not equal )
The form (5) is created by negating an equation. It is therefore usually not specifically addressed in mathematics.
Inequalities are forms of statement . The functional terms occurring on both sides of an inequality usually contain variables that represent elements from the definition range of the respective terms. If these variables are replaced by fixed elements of the respective domains of definition ( insertion ), statements are made which are either true or false.
Transformation of inequalities
Similar to equations, it is also possible for inequalities to convert them into equivalent inequalities . Equivalent inequalities have the same solution sets, so transforming inequalities is important for solving inequalities, which is what the following section will look at.
In the following, important rules for equivalent inequalities for the comparison symbols <and> and for terms in the field of real numbers are presented. These equivalence transformation rules apply analogously to the comparison symbols ≤, ≥ and ≠. In addition, further rules for non-equivalent transformations of inequalities are offered, which are often required in analysis - for example for proofs of convergence using epsilontics .
Reversibility
Inequalities can be reversed:
Laws of monotony in connection with the basic arithmetic operations
Addition and subtraction
For any real-valued Terme , , and the following applies:
- It is exactly when .
- It is exactly when .
The same terms can therefore be added or subtracted on both sides of an inequality without changing the solution set of the inequality. For example, the inequality is simplified by subtracting the term on both sides to give the equivalent inequality .
In addition, other rules apply with regard to the addition:
- Out and follows .
- Out and follows .
- Out and follows .
- Out and follows .
Multiplication and division
For any terms , and we have:
- From follows .
- From follows .
- Out and follows and .
- Out and follows and .
The following rule of thumb applies here:
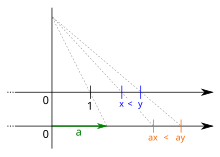
- In the case of point calculations with a real number> 0, the comparison symbols are retained, while they are reversed in the case of point calculations with a real number <0.
For example, the inequalities and are equivalent, as seen by dividing through .
In addition, other rules apply with regard to the multiplication within the group of positive real numbers :
- Out and follows .
- Out and follows .
- Out and follows .
- Out and follows .
Apply a function
By applying a strictly monotonic function to both sides of an inequality, one again obtains an inequality with the same solution set as the original inequality.
Similar to the monotony laws, however, the comparison symbol may also have to be rotated here. If you use a strictly monotonically increasing function on both sides, the comparison symbol does not change, but if you use a strictly monotonically decreasing function: In this case, the comparison symbol must then be replaced by the corresponding reversed symbol , analogous to the comparison symbol by the symbol and vice versa.
Examples
The natural logarithm and the root function are strictly monotonically increasing functions and can therefore be used to transform inequalities without having to rotate the comparison symbols. If there are two terms, then for example applies accordingly
However, caution is advised when it comes to exponential functions which, depending on their base, can be strictly monotonically increasing, but also decreasing:
The same applies to logarithms of any exponent:
For example:
Solving inequalities
A question when dealing with inequalities is - similar to the solution of equations - the question of the solution set of the inequality. The question to be answered here is whether and, if so, which elements of the domains of definition deliver a true or false statement when inserted into the two terms. An important technique for finding the solution set is to transform the inequality into a simpler form.
Known inequalities
In all mathematical sub-areas there are theorems about the validity of inequalities. This means that certain mathematical statements ensure the correctness of a given inequality for a certain set of definitions under certain circumstances. Some important inequalities are briefly mentioned below.
Triangle inequality
After the triangle is in the triangle , the sum of the lengths of two sides and always at least as great as the length of the third side . That means formal .
This inequality can be generalized to many mathematical objects. For example, the inequality is
for the absolute value function a generalization of the aforementioned inequality and applies to all real numbers. It is also called the triangle inequality. This inequality can also be generalized for the absolute value of complex numbers or for integrals (see Minkowski inequality ).
Cauchy-Schwarz inequality
So let Prähilbert space be a vector space with scalar product and let and elements be off , then the inequality always holds
Equality applies if and only if and are linearly dependent . Vector spaces with a scalar product occur in many mathematical sub-areas. Therefore, the Cauchy-Schwarz inequality is also important in many sub-disciplines of mathematics, for example it is used in linear algebra , integration theory and probability theory.
Extension of the term
So far, this article has only considered inequalities whose terms take on values in the real numbers. The term inequality is occasionally - but not uniformly - extended to, for example, complex numbers , vectors or matrices . In order to be able to consider inequalities for these objects, the four comparison symbols <, ≤,> and ≥ - in the following also called relations - must first be defined for these objects.
Complex numbers
The set of complex numbers , together with the usual addition and multiplication, is a field , but it is not possible to choose a relation ≤ in such a way that it becomes an ordered field . That is, it is not possible that a relation on both the trichotomy , the transitivity and the monotony law is satisfied. However, sometimes a relation is created by
is defined. Complex numbers and denote the real part or the imaginary part of a complex number. This definition of the relation fulfills the trichotomy and transitivity laws.
Column vectors
It is also possible to define relations for column vectors . Let be two column vectors with and where and are real numbers. You can then go through relations on , for example
and through
define. The relations ≥ and> can also be explained in the same way. However, it is not possible here to compare all elements with one another. For example, none of the four comparison symbols can describe a relationship between the elements and .
Further examples
- It is defined exactly when positive is definite . Are , then if and only if . Similarly, or (semidefinite) can also be defined.
- Let be a real Banach space and a cone . Are , then if and only if .
See also
- Inequality of Guha
- Hilbert's inequality
- Mulholland inequality
- Popoviciu's inequality
- Wallis inequalities
literature
- Edwin F. Beckenbach , Richard Bellman : Inequalities (= results of mathematics and their border areas . Volume 30 ). 4th edition. Springer Verlag , Berlin, Heidelberg, New York, Tokyo 1983, ISBN 3-540-03283-5 .
- Walter Gellert, Herbert Kästner , Siegfried Neuber (Hrsg.): Fachlexikon ABC Mathematik . Verlag Harri Deutsch, Thun and Frankfurt / Main 1978, ISBN 3-87144-336-0 .
- GH Hardy , JE Littlewood , G. Pólya : Inequalities . Reprint (of the 2nd edition 1952). Cambridge University Press , Cambridge 1964.
- Harro Heuser : Textbook of Analysis . Part 1. 17th edition. Vieweg + Teubner Verlag , Wiesbaden 2009, ISBN 978-3-8348-0777-9 ( MR2502662 ).
- DS Mitrinović : Analytic Inequalities . In cooperation with PM Vasić (= The basic teachings of the mathematical sciences in individual representations with special consideration of the areas of application . Volume 165 ). Springer Verlag , Berlin ( inter alia ) 1970, ISBN 3-540-62903-3 ( MR0274686 ).
References and footnotes
- ↑ inequality . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 978-3-8274-0439-8 .
- ↑ Calculating with inequalities . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 978-3-8274-0439-8 .
- ↑ Many of these rules can be applied to computing with inequalities in arranged groups .
- ↑ Tobias Hemmert: Complex numbers: construction from the real numbers, representation and application in physics . 1st edition, 2010, ISBN 978-3-656-00717-3 , page 7.