Linear equation

This article covers linear equations in linear algebra; for linear equations in analytical geometry see straight line equation .

A linear equation is a mathematical determining equation in which only linear combinations of the unknowns occur. A characteristic of a linear equation is that each unknown is only in the first power , i.e. not, for example, squared (see quadratic equation ). Typically, the unknowns of a linear equation are scalars , mostly real numbers . In the simplest case of a scalar unknown , a linear equation has the form ${\displaystyle x}$

${\displaystyle a\cdot x=b}$,

where and are constants . However, there are also linear equations with several unknowns and with other mathematical objects as unknowns, for example sequences ( linear difference equations ), vectors ( linear equation systems ) or functions ( linear differential equations ). In the general case, a linear equation has the form ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle T(x)=b}$,

where is a linear map . ${\displaystyle T}$

Homogeneous linear equations are special linear equations where the constant term of the equation is zero . The solutions of a homogeneous linear equation form a subspace of the vector space of the unknown and thus have special properties such as the validity of the superposition principle . The solutions of an inhomogeneous linear equation, on the other hand, form an affine subspace , so every solution of an inhomogeneous linear equation can be represented as the sum of the solution of the associated homogeneous equation and a particulate solution. The solution space of a linear equation can be characterized via the core and the coke core of the linear mapping . ${\displaystyle b}$

Linear equations and their solutions are studied in particular in linear algebra and linear functional analysis , but they also play a role in number theory .

Scalar linear equations

Often the unknowns in linear equations are scalars (mostly real or complex numbers ). Such linear equations are then special algebraic equations of degree 1.

Linear equations with one unknown

A scalar equation with an unknown is called linear if it is converted into the form by equivalence transformations (see Solving equations ) ${\displaystyle x}$

${\displaystyle a\cdot x=b}$

can be brought. Where and are constants that do not depend on. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle x}$

Is , the value of the unknown with which the equation is satisfied can be determined by dividing on both sides by : ${\displaystyle a\neq 0}$ ${\displaystyle x}$ ${\displaystyle a}$

${\displaystyle x={\frac {b}{a}}}$

If and are, the equation has no solution. If and are, there are infinitely many solutions, because then each one satisfies the equation. ${\displaystyle a=0}$ ${\displaystyle b\neq 0}$ ${\displaystyle a=0}$ ${\displaystyle b=0}$ ${\displaystyle x}$

Examples

The solution to the linear equation

${\displaystyle 3\cdot x=24}$

obtained by both sides by 3 divided so that only the unknown on the left side is left: ${\displaystyle x}$

${\displaystyle x={\frac {24}{3}}=8}$.

The linear equation

${\displaystyle 0\cdot x=7}$

has no solution while the linear equation

${\displaystyle 0\cdot x=0}$

for each is fulfilled. ${\displaystyle x}$

Linear equations with two unknowns

The solution set of the linear equation ${\displaystyle 3x+4y=12}$

A scalar equation with two unknowns and is called linear if it is converted into the form by equivalent conversions ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle a\cdot x+b\cdot y=c}$

can be brought, where , and are constants. The solutions form straight lines in two-dimensional space , unless both and apply. One then speaks of the coordinate form of a straight line equation . Otherwise the solution set is either the whole two-dimensional space or empty . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle a=0}$ ${\displaystyle b=0}$ ${\displaystyle (c=0)}$ ${\displaystyle (c\neq 0)}$

The solution to such an equation is often given in parametric representation . To do this , one solves the equation for one of the unknowns, for example what, if , ${\displaystyle y}$ ${\displaystyle b\neq 0}$

${\displaystyle y=(c-a\cdot x)/b}$

and treats the other unknown as a free parameter . This can be used as a ${\displaystyle x}$ ${\displaystyle t}$

${\displaystyle x=t}$  and     with   ${\displaystyle y=(c-a\cdot t)/b}$ ${\displaystyle t\in \mathbb {R} }$

write. In this way it becomes clear that, although the equation contains two unknowns, the solution space is only one-dimensional, i.e. only depends on one parameter . The parametric representation itself is not clear. Is , can the equation after dissolving and choose as free parameters. Other parameterizations are also possible, but they describe the same set of solutions. ${\displaystyle t}$ ${\displaystyle a\neq 0}$ ${\displaystyle x}$ ${\displaystyle y}$

example

The solution set for the linear equation

${\displaystyle 3\cdot x+4\cdot y=12}$

is by resolving for as ${\displaystyle y}$

${\displaystyle x=t}$  and     with   ${\displaystyle y=(12-3\cdot t)/4}$ ${\displaystyle t\in \mathbb {R} }$

given. The function graph of the straight line described is then obtained from the straight line equation

${\displaystyle f(x)=(12-3\cdot x)/4=-(3/4)\cdot x+3}$.

Linear equations with several unknowns

The solution of a real linear equation with three unknowns is generally a plane.

In general, a scalar equation with unknowns is called linear if it is converted into the form by equivalent conversions ${\displaystyle n}$ ${\displaystyle x_{1},x_{2},\dotsc ,x_{n}}$

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dotsb +a_{n}x_{n}=b}$

can be brought, where and are constants. So only linear combinations of the unknowns may occur. The solutions of such equations are generally -dimensional subsets ( hyperplanes ) of the associated -dimensional space. If the solution set is either the entire -dimensional space or empty . ${\displaystyle a_{1},a_{2},\dotsc ,a_{n}}$ ${\displaystyle b}$ ${\displaystyle (n-1)}$ ${\displaystyle n}$ ${\displaystyle a_{1}=a_{2}=\dotsb =a_{n}=0}$ ${\displaystyle n}$ ${\displaystyle (b=0)}$ ${\displaystyle (b\neq 0)}$

The parametric representation of the solution set is again obtained in the general case by solving the equation for one of the unknowns, for example if , ${\displaystyle x_{n}}$ ${\displaystyle a_{n}\neq 0}$

${\displaystyle x_{n}=(b-a_{1}x_{1}-\;\cdots \;-a_{n-1}x_{n-1})/a_{n}}$,

and the other unknowns as free parameters to conceiving. The solution set is thus given as ${\displaystyle t_{1}}$ ${\displaystyle t_{n-1}}$

${\displaystyle x_{1}=t_{1},\dotsc ,x_{n-1}=t_{n-1},x_{n}=(b-a_{1}t_{1}-\dotsb -a_{n-1}t_{n-1})/a_{n}}$  with   . ${\displaystyle t_{1},\dotsc ,t_{n-1}\in \mathbb {R} }$

Because parameters can be freely selected, the solution space is -dimensional. Here, too, the parameter representation is not unambiguous; the equation can also be solved for one of the other unknowns, provided the associated coefficient is not equal to zero, or another parameterization can be selected. ${\displaystyle n-1}$ ${\displaystyle (n-1)}$

example

The set of solutions to the linear equation with three unknowns

${\displaystyle 3\cdot x_{1}+2\cdot x_{2}+x_{3}=7}$

is a plane in three-dimensional space with representation

${\displaystyle x_{1}=t_{1},\;x_{2}=t_{2},\;x_{3}=7-3\cdot t_{1}-2\cdot t_{2}}$  with   . ${\displaystyle t_{1},t_{2}\in \mathbb {R} }$

General linear equations

Linear maps

In general, linear equations are defined using linear maps . An equation of form

${\displaystyle T(x)=b}$

is called linear if is a linear mapping and if is independent of . The mapping maps from a vector space to a vector space , where and are. Both vector spaces are defined over a common body . A mapping is linear when for constants ${\displaystyle T}$ ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle T\colon V\to W}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle x\in V}$ ${\displaystyle b\in W}$ ${\displaystyle K}$ ${\displaystyle \lambda ,\mu \in K}$

${\displaystyle T\left(\lambda x+\mu y\right)=\lambda T\left(x\right)+\mu T\left(y\right)}$

applies.

example

Is and , then is a real vector and a real number. One now chooses for the linear mapping ${\displaystyle V=\mathbb {R} ^{n}}$ ${\displaystyle W=\mathbb {R} }$ ${\displaystyle x=(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}}$ ${\displaystyle b\in \mathbb {R} }$ ${\displaystyle T}$

${\displaystyle T(x)=a\cdot x}$

with a constant vector , where is the standard scalar product of the two vectors, then one obtains the linear vector equation ${\displaystyle a=(a_{1},\dotsc ,a_{n})\in \mathbb {R} ^{n}}$ ${\displaystyle (\cdot )}$

${\displaystyle a\cdot x=b}$,

which is equivalent to the above scalar linear equation with unknowns. The linearity of follows directly from the linearity of the scalar multiplication ${\displaystyle n}$ ${\displaystyle T}$

${\displaystyle T(\lambda x+\mu y)=a\cdot (\lambda x+\mu y)=\lambda (a\cdot x)+\mu (a\cdot y)=\lambda T(x)+\mu T(y)}$.

homogeneity

A homogeneous and an inhomogeneous scalar linear equation with two unknowns and ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$

A linear equation is called homogeneous if is, that is, if it has the form ${\displaystyle b=0}$

${\displaystyle T(x)=0}$

has, otherwise a linear equation is called inhomogeneous. Homogeneous linear equations have at least the zero vector

${\displaystyle x=0}$

as a solution, there

${\displaystyle T(0)=T(0\cdot 0)=0\cdot T(0)=0}$

applies. Conversely, inhomogeneous linear equations are never satisfied by the trivial solution.

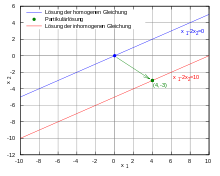
example

The solution of the homogeneous linear equation with two unknowns and ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$

${\displaystyle 3x_{1}+4x_{2}=0}$

is a straight line in two-dimensional space that goes through the zero point . The solution to the inhomogeneous equation

${\displaystyle 3x_{1}+4x_{2}=12}$

is a straight line parallel to it , but which does not contain the zero point.

Superposition

Superposition principle in the linear equation : solution of the homogeneous equation (blue), particle solution (green) and solution of the inhomogeneous equation (red) ${\displaystyle x_{1}-2x_{2}=10}$

→ Main article : Superposition (mathematics)

Homogeneous linear equations have the superposition property : Let and two solutions of a homogeneous linear equation, then there is also a solution of this equation. In general, it is even true that all linear combinations of solutions of a homogeneous linear equation with constants and solve this equation since ${\displaystyle {\hat {x}}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle {\hat {x}}+{\bar {x}}}$ ${\displaystyle c{\hat {x}}+d{\bar {x}}}$ ${\displaystyle c}$ ${\displaystyle d}$

${\displaystyle T(c{\hat {x}}+d{\bar {x}})=T(c{\hat {x}})+T(d{\bar {x}})=cT({\hat {x}})+dT({\bar {x}})=0+0=0}$

applies. By including and the superposition property, the solutions of a homogeneous linear equation form a subspace of . ${\displaystyle x=0}$ ${\displaystyle V}$

Furthermore, the solution of an inhomogeneous equation can be represented as the sum of the solution of the associated homogeneous equation and a particular solution: Let a concrete solution of an inhomogeneous linear equation and be the general solution of the associated homogeneous problem, then the general solution of the inhomogeneous equation is there ${\displaystyle {\bar {x}}}$ ${\displaystyle y}$ ${\displaystyle y+{\bar {x}}}$

${\displaystyle T(y+{\bar {x}})=T(y)+T({\bar {x}})=0+b=b}$

applies. The solutions of an inhomogeneous linear equation thus form an affine subspace over the vector space of the associated homogeneous equation.

Conversely, the following applies accordingly: If and are two solutions of an inhomogeneous linear equation, then solves the associated homogeneous equation, da ${\displaystyle {\hat {x}}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle {\hat {x}}-{\bar {x}}}$

${\displaystyle T({\hat {x}}-{\bar {x}})=T({\hat {x}})-T({\bar {x}})=b-b=0}$

applies.

example

A concrete solution to the inhomogeneous equation

${\displaystyle x_{1}-2x_{2}=10}$

is

${\displaystyle {\bar {x}}_{1}=4,{\bar {x}}_{2}=-3}$.

Are now the solutions of the corresponding homogeneous equation ${\displaystyle y=(y_{1},y_{2})}$

${\displaystyle y_{1}-2y_{2}=0}$,

so all with , then the inhomogeneous equation is generally solved by ${\displaystyle y}$ ${\displaystyle y_{1}=2y_{2}}$

${\displaystyle x=y+{\bar {x}}=(y_{1}+{\bar {x}}_{1},y_{2}+{\bar {x}}_{2})=(2y_{2}+4,y_{2}-3)=(2t+4,t-3)}$  with   . ${\displaystyle t\in \mathbb {R} }$

Dimension of the solution space

The solution space of a homogeneous linear equation is called the core of the linear mapping, its dimension is also called the defect . Due to the ranking , a finite-dimensional homogeneous linear equation applies to the dimension of the solution space ${\displaystyle \mathrm {ker} (T)}$

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(V)-\mathrm {rang} (T)}$.

Here is the rank of the image, i.e. the dimension of its image . The image of a picture is the set of values ​​that can be assumed for . ${\displaystyle \mathrm {rang} (T)}$ ${\displaystyle T(x)}$ ${\displaystyle x\in V}$

Due to the superposition property, the dimension of the solution space of an inhomogeneous linear equation is the same as that of the associated homogeneous equation, provided that a particular solution exists. This is exactly the case when the right-hand side is in the image of the figure, so it applies. The coke core of the linear mapping precisely describes the space of conditions that the right-hand side of a linear equation must meet in order for the equation to be solvable. Its dimension is ${\displaystyle b}$ ${\displaystyle b\in T(V)}$ ${\displaystyle \mathrm {coker} (T)=W/T(V)}$

${\displaystyle \mathrm {dim} (\mathrm {coker} (T))=\mathrm {dim} (W)-\mathrm {rang} (T)}$.

Examples

One chooses as vector spaces and as well as linear mapping ${\displaystyle V=\mathbb {R} ^{3}}$ ${\displaystyle W=\mathbb {R} }$

${\displaystyle T(x)=a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}}$,

where at least one of the coefficients is not equal to zero, then the image is of the whole space and thus ${\displaystyle a_{1},a_{2},a_{3}}$ ${\displaystyle T}$ ${\displaystyle W}$

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(\mathbb {R} ^{3})-\dim(\mathbb {R} )=3-1=2}$.

The solution space of the homogeneous linear equation has dimension 2 and is a plane in three-dimensional space. The solution space of the inhomogeneous equation is also a level here, since the equation, if for example , has the particulate solution . The coke core has dimension 0 here, so the equation can be solved for anything. ${\displaystyle T(x)=0}$ ${\displaystyle T(x)=b}$ ${\displaystyle a_{1}\neq 0}$ ${\displaystyle (b/a_{1},0,0)}$ ${\displaystyle b}$

If you choose instead

${\displaystyle T(x)=0x_{1}+0x_{2}+0x_{3}}$,

then all vectors from are mapped to zero and it applies ${\displaystyle V}$

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(\mathbb {R} ^{3})-\dim(\{0\})=3-0=3}$.

The solution space of the corresponding homogeneous linear equation is therefore the entire three-dimensional space. The solution space of the inhomogeneous equation is empty in this case, since the equation only has one solution. The coke core has dimension 1. ${\displaystyle b=0}$

Important types of linear equations

Linear Diophantine equations

→ Main article : Linear Diophantine equation

If one chooses vector spaces and over the whole numbers and ${\displaystyle V=\mathbb {Z} ^{n}}$ ${\displaystyle W=\mathbb {Z} }$

${\displaystyle T(x)=a\cdot x}$

with a constant coefficient vector , one obtains the linear Diophantine equations ${\displaystyle a\in \mathbb {Z} ^{n}}$

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dotsb +a_{n}x_{n}=b}$,

of which integer solutions are sought. Linear Diophantine equations have solutions if the greatest common divisor of the coefficients up to is a divisor of the right-hand side , i.e. if ${\displaystyle x=(x_{1},\dotsc ,x_{n})\in \mathbb {Z} ^{n}}$ ${\displaystyle a_{1}}$ ${\displaystyle a_{n}}$ ${\displaystyle b}$

${\displaystyle \operatorname {ggT} (a_{1},\dotsc ,a_{n})\;|\;b}$

applies. The solutions can then be given by combining the solutions of the homogeneous equation with a particulate solution that can be found using the extended Euclidean algorithm .

Linear vector equations

→ Main article : Linear system of equations

If one chooses the vector spaces and as well ${\displaystyle V=\mathbb {R} ^{n}}$ ${\displaystyle W=\mathbb {R} ^{m}}$

${\displaystyle T(x)=A\;\cdot \;x={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}\cdot {\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\\\end{pmatrix}}={\begin{pmatrix}a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}\\\end{pmatrix}},}$

wherein a real - matrix is obtained the linear vector equation ${\displaystyle A\in \mathbb {R} ^{m,n}}$ ${\displaystyle m\times n}$

${\displaystyle A\cdot x=b}$

with right-hand side and an unknown vector that just represents a system of linear equations . A linear system of equations is thus created by combining several scalar linear equations with one or more unknowns into one unit. The solution set of a linear system of equations is then the intersection of the solutions of the individual equations. A linear system of equations can be solved precisely if the rank of the coefficient matrix is equal to the rank of the extended coefficient matrix . Linear systems of equations can be solved, for example, with the aid of the Gaussian elimination method. ${\displaystyle b\in \mathbb {R} ^{m}}$ ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle A}$ ${\displaystyle (A\;b)}$

Linear difference equations

→ Main article : Linear difference equation

If one chooses the vector spaces as sequence spaces and, ${\displaystyle V=W=\mathbb {R} ^{\mathbb {N} }}$

${\displaystyle T((x_{n})_{n})=\sum _{i=0}^{k}a_{i}(n)x_{n-i}}$

one obtains the linear difference equation -th order ${\displaystyle k}$

${\displaystyle a_{0}(n)x_{n}+a_{1}(n)x_{n-1}+\dotsb +a_{k}(n)x_{n-k}=b(n)}$  for   , ${\displaystyle n\in \mathbb {N} ,n\geq k}$

where the unknown is a sequence and and are coefficients that may depend on, but must be independent of the terms of the sequence sought. The solution of a difference equation depends on the starting values and is then clearly defined. Linear difference equations can be explicitly solved by combining the solution of the homogeneous equation, which can be found using the characteristic equation , with a particulate solution. ${\displaystyle (x_{n})_{n}\in \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle a_{0}(n),\dotsc ,a_{k}(n)}$ ${\displaystyle b(n)}$ ${\displaystyle n}$ ${\displaystyle x_{0},\dotsc ,x_{k-1}}$

Linear ordinary differential equations

→ Main article : Linear ordinary differential equation

If one chooses the vector spaces and as function spaces with continuously differentiable functions and , one obtains -th order as linear ordinary differential operator by choosing ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle f\in C^{n}}$ ${\displaystyle g\in C^{0}}$ ${\displaystyle T}$ ${\displaystyle n}$

${\displaystyle T(f)=\left(\sum _{i=0}^{n}a_{i}(x){\frac {d^{i}}{dx^{i}}}\right)f}$

the linear ordinary differential equation

${\displaystyle a_{n}(x)f^{(n)}(x)+\dotsb +a_{1}(x)f'(x)+a_{0}(x)f(x)=g(x)}$,

where the coefficient functions and the right-hand side may depend on , but not on, the function sought and its derivatives . If a vector-valued function is used, one speaks of a linear differential equation system . Picard-Lindelöf's theorem gives the existence and uniqueness of the solution of ordinary differential equations of the first order . The general solution of the homogeneous equation can be given using the associated fundamental system, a particular solution can be found, for example, by varying the constants . ${\displaystyle a_{0},\dotsc ,a_{n}}$ ${\displaystyle g}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle f',\dotsc ,f^{(n)}}$ ${\displaystyle f}$

Linear partial differential equations

Are the vector spaces and also function spaces, and continuously differentiable functions of several variables are obtained by selecting a linear partial differential operator th order ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle f\in C^{n}}$ ${\displaystyle g\in C^{0}}$ ${\displaystyle T}$ ${\displaystyle n}$

${\displaystyle T(f)=\left(\sum _{\alpha _{1}=0}^{n}\cdots \sum _{\alpha _{m}=0}^{n}a_{\alpha }(x){\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{m}^{\alpha _{m}}}}\right)f}$

the linear partial differential equation

${\displaystyle \sum _{\alpha _{1}=0}^{n}\cdots \sum _{\alpha _{m}=0}^{n}a_{\alpha }(x){\frac {\partial ^{|\alpha |}f(x)}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{m}^{\alpha _{m}}}}=g(x)}$,

where , and are. Again, the coefficient functions and the right-hand side may depend on the coordinates to , but not on the function sought and its partial derivatives . In order for the solution of a partial differential equation to be uniquely determined, initial and / or boundary conditions must be specified. There are various approaches to solving linear partial differential equations, for example fundamental solutions , the method of characteristics or the separation approach . ${\displaystyle x=(x_{1},\dotsc ,x_{m})}$ ${\displaystyle \alpha =(\alpha _{1},\dotsc ,\alpha _{m})}$ ${\displaystyle |\alpha |=\alpha _{1}+\dotsb +\alpha _{m}}$ ${\displaystyle a_{\alpha }}$ ${\displaystyle g}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{m}}$ ${\displaystyle f}$

Linear integral equations

If the vector spaces and function spaces are sufficiently integrable, one obtains by choosing as the linear integral operator ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle T}$

${\displaystyle T(f)=\lambda f(x)+\int _{a}^{x}K(x,y)f(y)~dy}$

with integral kernel and constant prefactor is the linear integral equation ${\displaystyle K(x,y)}$ ${\displaystyle \lambda }$

${\displaystyle \lambda f(x)+\int _{a}^{x}K(x,y)f(y)~dy=g(x)}$,

which in the general case represents a Volterra integral equation of the 2nd kind . If both integration limits are fixed, it is a Fredholm integral equation. If one speaks of an integral equation of the first kind . ${\displaystyle \lambda =0}$

More linear operator equations

Examples of further linear operator equations with functions as unknowns are:

• Linear differential algebraic equations
• Linear integro-differential equations
• Linear stochastic differential equations

See also

• Quadratic equation
• Cubic equation
• Quartic equation
• Linearization

literature

• Hans Wilhelm Alt : Linear Functional Analysis. An application-oriented introduction . 5th edition. Springer-Verlag, 2008, ISBN 3-540-34186-2 .
• Bernd Aulbach : Ordinary differential equations . 2nd Edition. Spectrum Academic Publishing House, 2004, ISBN 3-8274-1492-X .
• Albrecht Beutelspacher : Linear Algebra. An introduction to the science of vectors, maps, and matrices . 7th edition. Vieweg, 2009, ISBN 3-528-66508-4 .
• Peter Bundschuh : Introduction to Number Theory . 6th edition. Springer-Verlag, 2010, ISBN 3-540-76490-9 .
• Gerd Fischer : Linear Algebra. An introduction for first-year students . 17th edition. Vieweg Verlag, 2009, ISBN 3-8348-0996-9 .
• Günter Gramlich: Linear Algebra . Fachbuchverlag Leipzig in Carl Hanser Verlag, 2003, ISBN 3-446-22122-0 .
• Jürgen Jost : Partial differential equations. Elliptical (and parabolic) equations . 1st edition. Springer-Verlag, 2009, ISBN 3-540-64222-6 .

Web links

Commons : Linear equations  - collection of images, videos and audio files

• MI Voitsekhovskii: Linear equation . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Linear Equation . In: MathWorld (English).
• Robert Milson: Linear Equation . In: PlanetMath . (English)