Linearization

In linearization , nonlinear functions or nonlinear differential equations are approximated by linear functions or by linear differential equations . Linearization is used because linear functions or linear differential equations can be calculated easily and the theory is more extensive than for non-linear systems.

tangent

Tangents on : blue green ${\displaystyle f(x)=\sin(x)}$
${\displaystyle x_{0}=0,}$
${\displaystyle x_{0}={\frac {3\cdot \pi }{4}}}$

The simplest method of linearization is to draw the tangent in the graph. Then the parameters of the tangent can be read off, and the resulting linear function ( point slope form of the straight line)

${\displaystyle y_{t}=f(x_{0})+{\frac {df}{dx}}{\bigg |}_{x_{0}}\cdot (x-x_{0})}$

approximates the original function around the point . It is the increase in point . ${\displaystyle x_{0}\;}$ ${\displaystyle {\frac {df}{dx}}{\bigg |}_{x_{0}}}$ ${\displaystyle x_{0}\;}$

If the function is in analytical form, the equation of the tangent can be given directly.

The relative error of the approximation is

${\displaystyle F(x)={\bigg |}{\frac {f(x)-y_{t}(x)}{f(x)}}{\bigg |}}$

The following applies to the function : ${\displaystyle f(x)=\sin(x)}$

${\displaystyle y(x)=\sin(x_{0})+\cos(x_{0})\cdot (x-x_{0})}$

The determination of the tangent corresponds to the determination of the linear term of the Taylor polynomial of the function to be approximated.

Applications

Linearization is used, among other things, in electrical engineering and control engineering for the approximate description of non-linear systems by linear systems .

The result of a network analysis may be a nonlinear system of equations. Under certain conditions, this can be converted into a linear system of equations . Not the only, but the simplest method of linearization is linearization in an operating point . Only this is described in the following sections.

Linearization of multiplication

In a signal flow plan , complex systems can be represented by a block diagram that is used for the qualitative visualization of mathematical models.

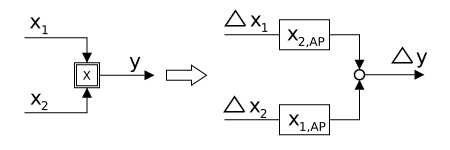
A multiplication in the signal flow diagram is replaced by an addition (working points x _{1, AP} , x _{2, AP} and y _AP have been omitted for a clearer representation) ${\displaystyle \Delta y=\Delta x_{1}\cdot x_{2,AP}+\Delta x_{2}\cdot x_{1,AP}}$

If there is a multiplication point in this signal flow diagram , this can be converted into an addition point by linearization.

In the following we denote by the product of two numbers and : ${\displaystyle y}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$

${\displaystyle y=x_{1}\cdot x_{2}}$

At the working point (AP) we can linearize the multiplication by writing as the sum of the working point and the difference : ${\displaystyle x_{1}}$ ${\displaystyle \Delta x_{1}=x_{1}-x_{1,AP}}$

${\displaystyle y=(\Delta x_{1}+x_{1,AP})\cdot (x_{2,AP}+\Delta x_{2}).}$

We can multiply this product according to the distributive law. The result is the sum:

${\displaystyle y=x_{1,AP}\cdot x_{2,AP}+x_{1,AP}\cdot \Delta x_{2}+x_{2,AP}\cdot \Delta x_{1}+\Delta x_{1}\cdot \Delta x_{2}.}$

We now assume that the ratio of the deviations from the working point and the working point itself is small: ${\displaystyle \Delta x_{i}}$

${\displaystyle {\frac {\Delta x_{i}}{x_{i,AP}}}\ll x_{i,AP},}$

and therefore the product is also small. The linearized multiplication is thus: ${\displaystyle e_{y}=\Delta x_{1}\cdot \Delta x_{2}}$

${\displaystyle y\approx x_{1,AP}\cdot x_{2,AP}+x_{1,AP}\cdot \Delta x_{2}+x_{2,AP}\cdot \Delta x_{1}.}$

example

Choose the numbers:

${\displaystyle x_{1}=2{,}4;\ x_{2}=110\Rightarrow y=x_{1}\cdot x_{2}=264.}$

Now the question arises of how to choose the working points. To simplify the calculation we round up , and to therefore choose: from The linearized product is so ${\displaystyle 2,4}$ ${\displaystyle 2}$ ${\displaystyle 110}$ ${\displaystyle 100}$ ${\displaystyle x_{1,AP}=2;\ x_{2,AP}=100\Rightarrow \Delta x_{1}=0{,}4;\ \Delta x_{2}=10.}$

${\displaystyle \Rightarrow y\approx 2\cdot 100+2\cdot 10+100\cdot 0{,}4=260}$

with the mistake . ${\displaystyle e_{y}=0{,}4\cdot 10=4}$

Linearization of the division

Linearization of a division shown in the signal flow diagram

We now consider the quotient of two numbers and : ${\displaystyle y}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$

${\displaystyle y={\frac {x_{1}}{x_{2}}}.}$

As with multiplication, we develop around the working point . With this we can write the quotient as follows: ${\displaystyle x_{i}=x_{i,AP}+\Delta x_{i}}$ ${\displaystyle x_{AP}}$

${\displaystyle y={\frac {x_{1,AP}+\Delta x_{1}}{x_{2,AP}+\Delta x_{2}}}.}$

Excluding the operating points gives for division:

${\displaystyle y={\frac {x_{1,AP}}{x_{2,AP}}}\cdot {\frac {1+{\frac {\Delta x_{1}}{x_{1,AP}}}}{1+{\frac {\Delta x_{2}}{x_{2,AP}}}}}.}$

We now want to linearize the numerator and the denominator of the fraction. For this we use the geometric series . The following applies to a null sequence : ${\displaystyle q^{k}}$

${\displaystyle \sum _{k=0}^{n}q^{k}={\frac {1-q^{n+1}}{1-q}}.}$

Here, in accordance with to choose. ${\displaystyle q=-{\frac {\Delta x_{2}}{x_{2,AP}}}}$ ${\displaystyle \vert q\vert \ll 1}$

Insertion provides the linearization

${\displaystyle {\frac {1}{1+{\frac {\Delta x_{2}}{x_{2,AP}}}}}\approx 1-{\frac {\Delta x_{2}}{x_{2,AP}}}.}$

The denominator of the above fraction can be linearized analogously. The linearized division can be written as:

${\displaystyle y\approx {\frac {x_{1,AP}}{x_{2,AP}}}\cdot \left(1+{\frac {\Delta x_{1}}{x_{1,AP}}}-{\frac {\Delta x_{2}}{x_{2,AP}}}\right).}$

Linearizing ordinary differential equations

A well-known example for the linearization of a nonlinear differential equation is the pendulum . The equation is:

${\displaystyle {\ddot {y}}(t)+D\cdot {\dot {y}}(t)+\omega ^{2}\sin(y(t))=0}$

The nonlinear part is . For small fluctuations around an operating point, this is approximated by: ${\displaystyle \sin(y)\;}$ ${\displaystyle y_{0}\;}$

${\displaystyle \sin(y)\approx \sin(y_{0})+\cos(y_{0})\cdot (y-y_{0})}$

The following applies to the working point : ${\displaystyle y_{0}=0\;}$

${\displaystyle \sin(y)\approx y\;}$ and thus the linearized differential equation

${\displaystyle {\ddot {y}}(t)+D\cdot {\dot {y}}(t)+\omega ^{2}\cdot y(t)=0}$.

These linearized differential equations are usually much easier to solve. For a mathematical pendulum (choose ) the equation can be solved by simple exponential functions, whereby the non-linearized one cannot be solved analytically. Further details on linearizing differential equations are described in the article on state space representation . ${\displaystyle D=0}$

Tangent plane

Representation as a signal flow plan

If a given function is to be linearized at a point , the Taylor formula is used. The result corresponds to the tangential plane at this point. ${\displaystyle f(x_{1},x_{2})\;}$ ${\displaystyle x_{10},x_{20}\;}$

The following applies to the function in the vicinity of the point : ${\displaystyle f(x_{1},x_{2})\;}$ ${\displaystyle x_{10},x_{20}}$

${\displaystyle y=\underbrace {f(x_{10},x_{20})} _{=const.}+\underbrace {{\frac {\partial f(x_{1},x_{2})}{\partial x_{1}}}{\bigg |}_{x_{10},x_{20}}\cdot (x_{1}-x_{10})+{\frac {\partial f(x_{1},x_{2})}{\partial x_{2}}}{\bigg |}_{x_{10},x_{20}}\cdot (x_{2}-x_{20})} _{=\Delta y}}$

Example:

${\displaystyle f(x_{1},x_{2})=x_{1}\cdot x_{2}}$

results in the tangential plane

${\displaystyle y=\underbrace {x_{10}\cdot x_{20}} _{=const.}+\underbrace {x_{20}\cdot (x_{1}-x_{10})+x_{10}\cdot (x_{2}-x_{20})} _{=\Delta y}}$

See also

• Taylor series
• Global linearization method

Web links

Wikibooks: Linearization of Resistive Sensors  - Learning and Teaching Materials

• Script of the TU Wien ( Memento from July 23, 2006 in the Internet Archive )
• Script from ETH Zurich