State space representation
The state space representation is one of several known forms of system description of a dynamic transmission system . The state space model is considered to be a suitable engineering method for the analysis and synthesis of dynamic systems in the time domain and is particularly efficient in the control engineering treatment of multi-variable systems , non-linear and time-variable transmission systems. All relationships between the input, output and state variables are represented in the form of matrices and vectors . The state space model is described by two equations, the first order state differential equation and the output equation .
history
The state space theory, known since the 1960s, comes from the USA by the mathematician and Stanford university teacher Rudolf E. Kálmán . It was created around the same time as the appearance of the first high-performance digital computers, which are indispensable for dealing with the state space display.
In the university area of the engineering disciplines of automation, mechatronics, electrical engineering, etc., the representation of the state space is increasingly taking on a larger area , especially in control engineering . According to some university professors, the representation of the state space has already been regarded as an essential technological impetus for aerospace travel, such as the flight to the moon carried out in the Apollo program in 1969.
Basics
The term state space representation is the description of a dynamic transmission system through its state variables (= state variables). The system-describing differential equation of the nth order with n concentrated energy stores is broken down into n differential equations of the 1st order and brought into a matrix / vector representation.
The status variables physically describe the energy content of the storage elements contained in a technical dynamic system. State variables are e.g. B. the voltage on a capacitor, the current in an inductance, in a spring-mass system the deflection of the spring, the speed of the mass. The number of state variables of the state vector corresponds to the dimension of the state space. All information of the dynamic transmission system is contained in the state vector at any point in time t (0) .
Essential terms for understanding the description of a transmission system in state space are the state space model and the applied normal form, according to which the state equations and associated matrices / vectors are designed. For systems that cannot jump, the state space model can be created directly from the coefficients of the differential equation describing the system or the associated transfer function.
According to the signal flow diagram of the normal control form , with the aid of the returned state variables, a dynamically advantageous state control loop can be formed, which can be simulated without a matrix display by means of numerical calculation of all signal quantities present.
Overview of the system descriptions
In the classical control theory before the 1960s, the analysis and calculation of control systems in the time domain was only of less importance than the methods in the frequency and s domain, such as the Laplace transformation , the frequency response and the root position method . Mainly linear time-invariant transfer elements with constant coefficients were dealt with. Nonlinear systems have been linearized.
To understand the theory of the state space representation, the following knowledge of the system descriptions is required:
- Ordinary differential equations of a transmission system
- The description of linear systems with concentrated energy stores (in contrast to systems with distributed stores → partial differential equation) is done with ordinary differential equations . The differential equation describes a linear transmission system with n energy stores by n derivatives of the system output variable y (t) and m derivatives of the input variable u (t) of the system.
- Example of the description of a 1st order delay element (PT1 element):
- with as the system time constant and the gain factor .
- Description of linear systems in the complex frequency range
- The transfer function is a mathematical description for the behavior of a linear, time-invariant system in the frequency domain (s-domain) with the complex variable s . In control engineering, it is the most common form of representation for describing the input and output behavior of transmission systems.
- All system properties such as the criteria of stability , poles , zeros , gain and time constants can be derived from the transfer function. The inverse transformation by means of the Laplace transformation enables the time behavior of a transmission system to be calculated as a function of the input signal.
- An essential finding in the linear system description is the fact that differential equations as well as transfer functions in polynomial representations of any order can be broken down into 3 simple basic forms of polynomials that have completely different signaling behavior, whether they are in the numerator or denominator of the transfer function.
- Example of the description of a 1st order delay element ( PT1 element ):
- Numerical description of linear and non-linear systems
- Relatively simple transmission system structures with non-linear elements, limiting effects and dead time systems can no longer be solved in a closed manner using conventional calculation methods in the continuous time domain. The numerical calculation in the discrete time range Δt offers a remedy.
- Instead of calculating the continuous behavior of the physical quantities of a dynamic system as f (t), it is converted into a quantized calculation method with constant small time intervals, the discrete time Δt. The dynamic system is described in its simplest form by 4 different first order differential equations with difference equations and calculated recursively algebraically . The essential feature of the recursion is the sequence k = (0, 1, 2, 3, ..., k n ), in which the calculation result of the previous sequence k-1 is added to the current discrete calculation result of the sequence k .
- Example of the description of a 1st order delay element (PT1 element with the gain factor K PT1 ) according to the Euler approximation :
- Various computer programs are available for the numerical calculation of transmission systems.
Definition of the state of a transmission system
While the above system descriptions describe the transmission behavior of a system, the description of a system in the state space means the current state of the system at a certain time t = 0.
From a physical point of view, the state of a dynamic system is determined by the energy content of the energy storage in the system. The state variables describe the energy content of the storage elements contained in the system. They cannot change suddenly when the system is stimulated.
The value of the state variables at this specific point in time t is the state of the system and is summarized by the vector .
The behavior of the transmission system is completely given at any point in time at the time t = 0 for t > 0, if
- the mathematical model of the transmission system is known,
- the initial values of the energy storage are known and
- the input variables of the system are known.
It follows:
With knowledge of the system status and all the signal variables acting on the system, the future system behavior for t> 0 can be predicted.
State of a dynamic system in the state space = state vector at the point in time .
- The state vector of a linear system completely determines the course of the output variable y (t) for with the course of the input signal u (t) .
- The number of state variables is the dimension of the state space.
Definitions of terms: state space, vector space, phase space, phase portrait
In the German-speaking world, the concept of state space representation for the older and still valid term system description in the state space did not emerge until after the 1970s.
In control engineering, the term "state space" of a dynamic transmission system is usually defined as follows:
"The state space is the n-dimensional vector space belonging to the state vector , in which every state is represented as a point and every change in state of the transmission system is represented as part of a trajectory ."
In general, however, the state space of dynamic systems can be a manifold that does not meet the requirements of a vector space. This has the same properties as a vector space only in a local environment around a point.
The system behavior of a dynamic transmission system in the state space using the example of a higher-order delay system can be graphically represented by:
- Graphic representation of the phase portrait
- In the state space representation for two-dimensional systems, the space spans an area. This relationship is called phase space and the resulting trajectory is called phase portrait .
- The phase portrait for systems without an input signal u (t) = 0 is always traversed clockwise to the origin, provided the system is stable.
- For 2 or 3-dimensional state vectors, graphic constructions are possible for understanding.
- Are z. For example, for a PT2 oscillator with damping D = 0.06, the input variable u (t) = 0 and the initial values and are given, then the trajectory (phase portrait) runs as a function of time in the x1-x2 diagram according to the proper movement of the system from an initial value in a spiral shape (typical for a vibrational link) to the origin zero ( ) after a finite, sufficiently long time.
- The trajectory of a PT2 element with damping D = 1 and the same initial values cannot wrap around the origin - as shown in the figure - but reaches it by a falling initial gradient on the shortest path.
- Recording of the course of the state variable f (t)
- By recording the course of the state variables as a function of time after a system input jump u (t), it becomes clear that the state variables of the transmission system behave dynamically much faster than the output variable .
- The use of this advantageous property is of great importance for the control behavior of a state control loop. The defining terms for the state control loop are state feedback and , compared to the conventional counterpart, output feedback .
- See in section Normal control form , third figure "Graphic representation of the status variables".
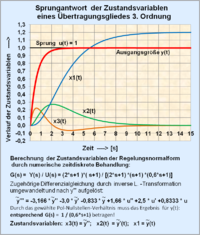
Example of state variables and state equations for a PT2 oscillator
Standard transfer function of a vibrating element ( PT2 element ) with conjugate complex poles (PT2 KK element):
The associated linear differential equation is determined by conversion using the inverse Laplace transform:
In the technical literature, the coefficients of the derivatives of y (t) (here T², 2 DT ) are represented with the letter a, for the right-hand side of the derivatives of u (t) with b and numbered consecutively:
The highest derivative is released from the coefficient by dividing all terms of the equation by and solving for :
The block diagram shown in the structure diagram corresponds to the classic variant of solving a differential equation with the aid of analog computing technology. This method has been known for a long time. Of course, we were only interested in the behavior of the output variable y (t).
Every derivative of the output variable y (t) is subjected to an integration. Each state variable is fed back to the input with the associated coefficient and subtracted from the input variable u (t).
A differential equation of the nth order requires n integrations for the solution. According to the block diagram for solving the differential equation of the 2nd order, there are 2 state variables as outputs of the integrators. By substitution, the derivatives of y (t) are used by the designation of the state variable x (t) as follows:
The differential equation with the new names of the state variables that have been introduced reads:
The conversion of the system-describing differential equation of the nth order into n-coupled differential equations of the 1st order takes place as follows:
If, according to the block diagram, e.g. If, for example, the state variable is offset from the output of the integrator to the input of the same integrator, then the derivation of .
The first-order state differential equations follow from this:
The state variables and form the so-called state vector .
These equations are written as vector differential equations in matrix form as follows:
and the initial equation:
There are various signal flow diagrams that lead to the solution of the differential equation and the determination of the state variables. According to the block diagram of the oscillating element, the quotient can lie to the left of the subtraction point, it can lie to the right of it, or the equation can be transformed so that the highest derivative has the coefficient 1. All of these measures lead to the same result for the output variable y (t). However, this does not apply to the definition of the coefficients of the state variables.
For transmission systems with poles and zeros, there is therefore a uniform standard form, preferably the "control standard form " for representing the signal flows.
State space model
The state space representation is based on a state space model.
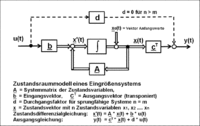
The block diagram with the signal flow diagram of the state space model shows a single-variable transmission system with an input signal u (t) and an output signal y (t) in a general representation for a linear transmission system with n differential equations of the first order. It corresponds to the system representation of the normal control form. Instead of a differential equation system of the nth order, there is a derivation of the n-dimensional state vector of the 1st order . This derivative is the input variable of an integrator; this results in the state vector .
The equations of state for the derivative of the vector and the output variable y (t) of a single variable system
can be read directly from the block diagram of the state space model.
The block diagram of the state space model has a uniform form, but is represented differently as a single or multiple variable system. In the multi-variable system, the vectors and occur instead of the scalar input and output variables u (t) and y (t) . The signal flows of matrices and vectors are shown in the block diagram by double lines.
Summary of the state space model:
- State space model and block diagram
- The block diagram with the signal flow diagram of the state space model is identical for all applications, regardless of whether it is a single-variable system or a multi-variable system. It represents the signal flow diagram of the normal control form for a linear system of the nth order with n differential equations of the first order. Therefore, it only requires one integrator to calculate the state vector .
- The state space model always relates to a specific application in the description of a transmission system.
- The value description relates to all signals in the system. These include the values of the system status , the input variable u (t), the output variable y (t) and the initial values of the system .
- As shown in the block diagram, the signals are linked to the system matrix, the input and output vector. In multi-variable systems, the single-column input vector becomes the input matrix and the single-row output vector becomes the output matrix.
- System matrix
- The system matrix contains the coefficients of the state variables. By using normal forms such as the normal control form, the system matrix can be created according to a relatively simple scheme. The coefficients of a transmission system of the nth order are in the bottom line of the matrix in the normal control form. They can be taken directly from the differential equation describing the system or the associated transfer function.
- In multi-variable systems with coupled transmission elements, the determination of the state variables and the design of the system matrix can be time-consuming. A coupled transfer function or the associated differential equation can be determined for each output variable . From this - possibly after linearization - the coefficients for the n * n system matrix are formed.
- Linear and non-linear systems
- The state space model describes linear transfer systems using linear differential equations or transfer functions.
- Non-linear transmission systems require an increased mathematical effort. Nonlinear systems, e.g. B. in practice often occurring with a broken characteristic curve due to signal limitations, cannot be described with linear differential equations. For them as well as for systems with dead times, numerical calculation is used.
- State differential equation and output equation
- The state space model is described with the aid of the signal flows shown by 2 equations, the state differential equation and the output equation (also output equation).
- The state differential equation is a 1st order vector differential equation that describes the system dynamics. It indicates how the input signal u (t) influences the individual memories and how these memories are linked to one another.
- The algebraic output equation describes how the output signal y (t) is related to the system states.
- State space model equations:
| equation | With single-size systems | With multi-size systems |
|---|---|---|
|
State differential equation (also state equation) |
||
| Output equation |
For |
For |
- Meaning of the signals and system blocks of the state space model:
| meaning | Single size system | Multi-size system |
|---|---|---|
| Derivation of the state vector | ||
| State vector | ||
| State variable | ||
| Initial conditions vector | ||
| Input signals |
Input variable |
Input variable vector |
| Output signals |
Output variable |
Output variable vector |
| System matrix | ||
| Input matrix |
Input vector |
Input matrix |
| Output matrix |
Output vector (transposed) |
Output matrix |
| Passage matrix |
Passage factor for |
Passage matrix for |
Indexing:
- Matrices = capital letters with underscore,
- Vectors = lowercase letters with underscore,
- Transposed vector representation, example:
- By default, a vector is always in column form. To get a row vector, a column vector must be transposed.
Linear state differential equations of a multi-variable system
According to specialist literature, dynamic systems are generally regarded as multi-variable systems in the state space. Single-variable systems are - in contrast to classic control technology - a special case.
Linear transmission systems with several input and output quantities can be described with linear state differential equations.
The output equations for linear systems have the following forms:
These equations, shown in vector notation, can also be reproduced in matrix notation.
State differential equations of the multiple variable systems
Output equations of the multi-variable systems:
Linear state differential equations of the single variable systems
Single variable systems have only one input variable and one output variable . The input matrices and output matrices merge into the input vector and output vector .
Initial equation of the single variable systems:
Normal forms in the state space
In the description of states with normal forms , the equations of state take on particularly simple and useful forms for certain calculations. For the normal forms, the system description of the linear transfer system is based on the differential equation or the associated transfer function.
The most popular normal forms include:
- Normal control form (also referred to as Frobenius form, normal control form or 1st standard form)
- Observation normal form
- Canonical normal form (also called Jordan normal form or diagonal form).
The normal forms can be recognized in the system matrix by the local position of the coefficients.
Normal control form
The signal structure of the normal control form presents itself as an analog time-continuous system which reproduces the solution of the differential equation with the input variable and at the same time shows the state variables .
The block diagram of the normal control form shows the implementation and solution of the differential equation in the physical analog signal flows of the state variables including the output variable for a given input variable. It can be seen as a further development of the method known in analog computing technology for solving an nth order differential equation with integrators. If the coefficients of the state variables are known, the signal flows can be determined directly using numerical calculations for any input signals and displayed graphically.
The simplified example of the 2nd order block diagram signal flow diagram shows a transmission system that contains only poles. For any systems with poles and zeros in the normal control form, the signal flow diagram must be extended by the derivatives of the input variable so that the terms add to the output variable y (t).
Transfer function and associated differential equation in polynomial representation
The transfer function of a linear transfer system in polynomial representation is defined as the ratio of output signal to input signal as a function of the complex frequency s. It arises under the prerequisite that the initial conditions of the energy storage device of the output variable Y (s) are set to zero:
N = number of poles and m = number of zeros in the system:
- n> m: This corresponds to the normal case in control engineering, i.e. H. the number of poles n are greater than that of the zeros m. The system is not capable of jumping.
- m = n: This relationship with the same number of poles and zeros only occurs in exceptional cases. The system is capable of jumping, i. H. a sudden change in the input variable is transmitted to the output without delay.
- m> n: These systems cannot be treated with the state space representation. Nor are they technically feasible.
The associated differential equation of the transfer function results from the inverse Laplace transform .
The highest degree of derivation of indicates the number of storage elements in the route.
State variables arise from the poles of the transmission system
The state variables of a linear system of the nth order with n energy stores always arise from the poles. If the transmission system also has zeros - i.e. differentiating components - the state variables with the coefficients of the derivatives of the input variable u (t) are added to the output variable y (t). Explanation from systems theory: The poles of a transfer function determine the speed of the system movement and the stability. The zeros of a transfer function only affect the amplitudes of the system.
Indexing the derivatives of y (t)
Because the output variable of the transmission system is already denoted by y (t), the differential equation describing the system must be indexed with the derivatives of y (t). Instead of the symbol y (t), the differential equation receives the symbol and u (t) is introduced by. In the state space representation, the derivatives of y (t) disappear and are replaced by the state variables x (t).
This will make the state variables
In the block diagram of the normal control form, the derivatives of are replaced by the state variables so that they no longer appear.
Definition of pole-zero ratio and coefficients of the differential equation
The normal control form applies to linear systems with n poles and m zeros up to n → m.
With the help of numerical discrete-time calculation methods, the solution of the differential equation y (t) and the course of the state variables for a given input signal u (t) can easily be determined.
The associated matrix representation for a non-jumpable system of order n, which is common in control engineering, is in the normal control form with the following conditions:
The system-describing transfer function or the associated differential equation are transformed so that the coefficient of the highest derivative of y (t) equals 1. All coefficients are divided by and reordered.
Example: State variables for a 4th order transmission system
The transfer function of a transmission system e.g. B. 4th order (with the derivatives of the 3rd order input variable) with the permissible restriction n> m for control engineering and the coefficient of the highest derivative of y (t) :
The associated differential equation reads for a 4th order transmission system with the allowable restrictions m <n:
The following equations of state result from the differential equation according to the known scheme (substitution of the derivatives of y (t) by x (t)):
These equations can always be converted for the state space representation in matrix notation as state differential equations for single variable systems according to the same scheme:
Output equations for single-variable systems:
The state space model in the normal control form is understood to be a uniform form of the matrix representation with the following advantageous properties:
- The numerator coefficients of the transfer function (zeros) are only contained in the output vector ,
- The denominator coefficients of the transfer function (poles) are only included in the system matrix ,
- The system matrix has a special structure. Of the n · n elements only are n elements of the last line of the transmission system depends,
- The input vector is independent of the system properties.
Controllability and observability of transmission systems
Model of a transmission system
For the analysis, synthesis and regulation of real transmission systems ( controlled systems ), which are generally present as a hardware system, a mathematical model of the system is required.
Models in the form of differential equations describe the behavior of the system over time exactly. If these differential equations or associated transfer functions are not given, the behavior over time of a hardware system can be determined by experimental identification measures ( experimental system identification ) with the aid of test signals .
In the basic procedure, the identification algorithm for the model parameters is changed until the difference between the output variables y (t) - y model (t) for a given input signal u (t) approximately disappears within an arbitrary time sequence of the measured original output with the model output.
The model defines the structure of a signal flow plan from which the state variables can be derived. If the system has n energy stores, the n state variables are summarized by the state variable vector . If the input variable u (t) and the coefficients of the state variables of the route are known, the output variable y (t) can be calculated.
The transmission system (controlled system) must be controllable. All status variables must be available. Pole-zero compensation in the state space is not permitted because information is lost.
While the problem of controllability and observability does not always arise with single-variable systems, because single-variable systems are presented in a simpler manner, in the case of coupled multi-variable systems, a check may be required according to known rules of the controllability matrix and the observability matrix.
Controllability of a single variable system: For a system with only one control variable , the matrix becomes a column vector .
Observability single variable system: For a system with only one output variable , the matrix becomes a line vector
This results in a simplified controllability matrix and a simplified observability matrix.
Controllability
With state control, all state variables are fed back to the input of the system. All status variables must be available to carry out a status control. This condition is fulfilled when the manipulated variable of the controller affects all status variables.
A system is controllable if it can be brought from any initial state to any final state after a finite time.
In general, the following applies to the controllability in relation to the signal quantities:
- A system is completely state-controllable if, for each initial time, each initial state can be brought into any desired final state after a finite time by an unlimited control vector .
A system of the nth order is fully state controllable if the controllability matrix has the rank .
If all states (state variables) of a system can be controlled, the system can also be controlled.
Observability / observer
State controls require all state variables of a transmission system. The state variables are determined by measurement from the controlled system. If this is the case, this corresponds to “complete observability”.
Often not all state variables can be measured for technical or commercial reasons. For this reason, individual non-measurable status variables are calculated from the known and existing input and output variables of the controlled system. Condition observers who perform this task are additional control systems. You reconstruct state variables from the course of the input and output variables on a model of the controlled system. The input variable u (t) must be known.
Condition observers can only be implemented if the system to be observed can be observed, which is the case with the vast majority of technical controlled systems.
A linear transmission system can be observed if the initial state of the state vector can be determined after a finite time by measuring the output variable y (t) .
- A system is said to be fully observable if every initial state can be determined exactly from the measurements of the output signal y (t) in a certain time interval from .
An n-th order system is completely observable if the observability matrix has the rank .
State controller with observer
The separation principle is used to implement the condition observer. It allows the state feedback and the observation to be designed separately. Such a procedure can be implemented with the "Luenberger observer". The controlled system and the observer with the model controlled system are connected in parallel at the input u (t). The output of both systems is monitored and used to correct the model controlled system.
The observer needs a model of the controlled system that is as precise as possible.
Due to the structure of the controlled system and identification methods using the step or impulse response of the controlled system, a model of the controlled system can be created which in most cases still has minor errors.
According to the procedure with the Luenberger observer, the controlled system output y (t) is compared with the model output and fed back additively via a control loop to the input of the model, so that the output of the controlled system and the output of the model are identical within a settling time. It is assumed that the unknown state vector and the determined model state vector are then almost identical.
For the state control loop, the determined state vector with evaluation factors for the desired dynamic behavior of the state control loop is subtracted from the reference variable w (t).
Regulation in the state space
With single- loop standard control loops, the output variable of the control loop is usually subtracted from the reference variable and then fed to the controller as a control difference . This procedure is known as output feedback in connection with the handling of systems in the state space.
A common controller design strategy for controlled systems with output feedback is relatively simple:
The transfer function of the overall control loop is simplified by means of pole zero point compensation of the controller and the controlled system of the open control loop. H. the order of the differential equation of the controlled system is reduced by setting the values of the controller's zeros to the values of the pole of the system. An I component of the controller avoids a permanent control deviation, but adds an additional pole. The parameter to be optimized is the loop gain . The step response of the controlled variable runs as a function from asymptotic to strongly overshooting until the setpoint is reached.
The state variables of a mathematical model of a controlled system can be determined from a common system-describing differential equation. The basis for solving the differential equation is the signal flow diagram with the graphic representation of the normal control form. The terms of the derivatives of the output variable are integrated and fed back to the system input with the associated coefficients.
For each derivative , the designation of the state variables is introduced as follows:
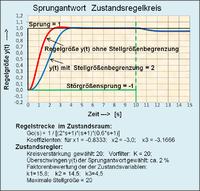
The time course of the state variables as a result of an input jump in the model shows the advantage of treating the system in the state space compared to a classic "output feedback" of the system. The status variables appear earlier than the output variable . This behavior is used in the state control loop in that the state variables are traced back to a target / actual difference with the reference variable .
State controller
Simulations of a state control loop can easily be carried out with a good model of the controlled system on a programmable computer. The description of the signal flow diagram of the controlled system and the controller in the state space can be done in the form of matrices as well as with difference equations . Depending on the order of the differential equation, all state variables are fed to a state controller, which acts on the input of the state space model of the controlled system. The feedback of all status variables creates a multi-loop control loop.
The linear state controller evaluates the individual state variables of the controlled system with factors and adds the resulting state products to a target / actual value comparison.
This state controller is not a P controller, although such an impression could arise according to the signal flow diagram. The state variables with evaluation factors fed back with the controller run through the arithmetic circuit once again to solve the differential equation with n integrators and form new circular variables, which results in differentiating behavior. Therefore, depending on the magnitude of the order of the differential equation of the system , the effect of the returned state variables corresponds to that of a controller.
The pole assignment ( pole specification ) of the closed control loop is used as the design strategy for determining the evaluation factors of the state controller .
Empirical settings of a model control loop are also easily possible. Because the integrators are connected in series, only the state variable is a stationary variable if the input variable is constant. All other state variables - assuming a stable controlled system - tend towards the value zero. After setting and optimizing the factor , a stable control loop of certain damping results with a proportional error compared to the controlled variable . The other factors of the state variables are consecutively z. B. set to optimize the transition behavior.
A pre-filter before the target / actual comparison corrects the static error between and .
Requirement for the feedback of the status variables:
- The controlled system must be controllable.
- All status variables must be available. Pole-zero compensation in the state space is not permitted because information is lost.
- In practice, the state variables can be measured on a controlled system, which is not always possible. Observers can remedy this by reconstructing the state variables if the route can be observed.
- Theoretically, n state variables of a system correspond to the outputs of the -fold differentiation of the output variable . Because of the parasitic time constants and amplification of the signal noise, which are unavoidable for implementation, this approach cannot be followed.
The state controller results in the following control properties of a control loop:
- dynamic behaviour
- Because the signal information of the state variables of the controlled system is available earlier than with the output feedback, the dynamic behavior of the control loop is more favorable than a control loop with output feedback. With a state controller, high demands on the control quality can be met.
- Differentiate through integration
- In the state control loop, the feedback of the state variables is differentiated through integrations. The disadvantages associated with differentiation, such as parasitic time constants and signal noise, do not occur. There are also no large manipulated variables when there are jumps in the input signal.
- State variable in the steady state
- In the stationary state of the state control loop, only the state variable shows a stationary value. All other status variables have the value zero because the integrators are connected in series.
- Behavior of the controlled variable
- The output variable (controlled variable) is not recorded by the state controller . If the controlled system has no zeros (differentiating components), then the state variable is proportional at all times . They differ in the coefficient .
- If there are zeros in the controlled system, then the output variable has a different time behavior than the state variable during the settling time (non-stationary state) .
- Behavior of the controlled variable with disturbance variables
- Depending on where the disturbance variables are attacked, undesirable properties occur. The fault at the output of the controlled system is not recorded. The disturbance variable at other parts of the controlled system is only reduced by the loop gain, but not controlled towards zero. The latter applies in the same way to every control loop that does not contain an I behavior.
- Pre-filter
- A steady-state accuracy of the controlled variable for the setpoint cannot be achieved through the state feedback. Even with a controlled system without zeros, i.e. without differential components, the state variable according to the normal control form is not identical to the output variable y (t). For this reason, the state feedback is often extended with a prefilter . The reference variable acts directly on the pre-filter. For simple requirements, a correction can be carried out by means of a factor in the prefilter so that the steady state is achieved.
The state controller in the property shown serves to understand its advantages. In its behavior as a PD controller, it allows a higher loop gain than in a control loop with an output feedback. There is no differentiating component within the state control loop.
In a comparison with a standard PD2 control and output feedback and otherwise the same circuit damping, the same controlled system and disturbance arising for this controller significant disadvantages such as large manipulated variables, very poor noise suppression and the manipulated variable limits of ( totzeitähnliches) phase behavior.
Depending on the requirements with regard to control deviation and interference suppression at the output of the controlled system, it can be inferior to a conventional PID standard controller. A control loop overlaid with a PI controller remedies these disadvantages. The state controller thus has considerably better properties.
The use of the state controller ultimately depends on a cost-benefit assessment.
State controller with superimposed control loop
For demanding control tasks with systems in the state space, it may be necessary to introduce a superimposed control loop for the state control loop with an output feedback. This eliminates all stationary problems for the correspondence of the reference variable with the controlled variable and constant disturbance components.
The use of a PI controller is recommended. According to the transfer function of the PI controller in the product illustration, the controller consists of the components I element and PD element. This controller only allows a temporary system deviation, provided that the reference variable and a possible disturbance variable are constant. A delay component (PT1 element) of the state control loop can be compensated for by the PD component. Signal noise from the PD element is reduced by the I element.
The following parameters must be taken into account when designing the higher-level PI state control loop:
- Manipulated variables
- Large manipulated variables in the control loop make a controlled system fast, provided the stability of the loop is not endangered. In many cases the controlled system limits a large manipulated variable. This means that a step response in large-signal behavior is delayed and distorted. This problem mostly occurs when using P and PD controllers. Nevertheless, a high P-loop gain in the small-signal behavior means that the control deviation is lower and the interference suppression is greater.
- Evaluation of the factors of the state coefficients
- The factors of the fed back state variables, the loop gain and the lead time of the PD component of the PI controller determine the dynamics of the state control loop. They are all interdependent.
- State variable in the steady state
- Stationary the state variable determines the output variable . All other status variables have the value zero. The superimposed control loop leads the controlled variable to the level of the reference variable , provided it is constant.
- Disturbance
- The size of the P-loop gain determines the dynamic reduction of attacking disturbance variables in the area of the controlled system. In the steady state, a constant disturbance variable has no influence because of the I component of the superimposed control loop.
A state controller with a superimposed PI control loop has clear dynamic advantages over a conventional, well-optimized control loop with the same controlled system and the same transient response.
Advantages:
- A higher loop gain allows better interference suppression,
- the manipulated variables are smaller in the step response for a given limit value of the overshoot,
- no parasitic time constant of the controller required,
- the pre-filter is omitted,
- the signal-to-noise components are low in the superimposed status control loop because there is no differentiation in the PI controller.
Disadvantages in general:
- The state variables are usually not available. They need to be measured.
- Possibly. the state variables must be reconstructed by an observer.
- As with all controllers with an I component, the controlled variable will overshoot excessively in the case of limitation by the controlled system in the step response. This effect is compensated for by a wind-up correction.
- Increased material expenditure, specially trained specialists required.
Mathematical concentrate of the rules and equations in the state space
Description of linear systems
Continuous time linear systems are given by the linear differential equation of the nth order
described. If the coefficients and are all constant, the Laplace transform can be carried out and the transfer function applies
- .
An n-th order differential equation can be converted into a system of n first-order differential equations
be convicted.
Discrete-time linear systems are described by the linear difference equation of the nth order
described. If the coefficients and are all constant, the z-transformation can be carried out and the transfer function applies
- .
A difference equation of the nth order can be converted into a system of n difference equations of the 1st order
be convicted.
Linear equations of state
For time-continuous systems the basic linear equations are in vector form:
The chaining of the individual states, including the accesses via the control variables (input variables), can be displayed via the matrices and . The matrix is referred to as the system matrix, the control matrix . The observation matrix describes the effects of the system on the output. The passage matrix describes the penetrations of the system , it is not at jump-capable systems zero.
Systems with one input and one output variable represent an important special case (SISO single input, single output systems). Here are and vectors and a scalar. The symbols , and are often used.
In many cases, instead of a continuous curve, only the system status at discrete points in time is of interest, for example the sampling points in the case of regulation by a digital computer. In this case, instead of a vector-valued function of time, there is a sequence of vectors. A difference equation then takes the place of the state differential equation.
The types of basic linear equations:
| System type | State space model |
| Continuously time invariant |
|
| Continuously time variant |
|
| Discrete time invariant |
|
| Discrete time variant |
|
| Laplace Transform Continuously Time Invariant |
|
| Z-Transform Discrete Time Invariant |
|
For the last two cases it was assumed that the initial state of the system is (see the differentiation theorem of the Laplace transformation and the difference theorem of the Z transformation).
The time-discrete representation of the state is made from the continuous form by means of discretization over a fixed time step size T in the form
won. Applies gives the integral
- .
The discrete form is particularly suitable for real-time calculations . In real time, the initial equation is calculated first, and only then the state difference equation to determine the states for the next calculation step. The time-continuous display, on the other hand, is well suited for simulations without real-time requirements, through numerical integration . The accuracy can be influenced here by the choice of the integration method and the adaptation of the static or dynamic step size.
The system matrix is of central importance, from which the eigenvalues and thus the system dynamics and their stability can be derived ( characteristic polynomial ). If the pass-through matrix is not a zero matrix , the system inputs have simultaneous influence on the outputs, which can lead to an algebraic loop .
If A, B, C, D are constant, the system is linear and time-invariant, i.e. H. a so-called LZI system.
Nonlinear equations of state
An n-th order nonlinear system can be described as a system of first order nonlinear differential equations
or more compact in vector notation
to be written.
The following applies to the rest point
If the deviation of the system from the rest point then applies
and
- .
The linearized representation
with the Jacobi matrices and results from a multi-dimensional Taylor expansion linearized around the rest point.
Similarity transformation
The state space representation is not unambiguous. There are an infinite number of state space representations for the same system. Instead of the usual state variables , you can also use a new set of state variables , if you can write through . where is a regular, linear transformation matrix, i.e. H. must be writable without adding inputs or derivatives.
The following then applies:
The new state space representation describes the same system. It goes without saying that all system properties remain unchanged during the transformation.
Transfer function
The "transfer function" of a continuous time-invariant state space model can be derived in the following way with vanishing initial conditions (x (0) = 0):
by the Laplace transform one obtains
which is substituted in the initial equation
and gives the transfer function
Here corresponds to the identity matrix .
General solution in the time domain
The general solution in the time domain can be obtained with the starting values :
Difficulties can arise with the matrix exponential function, which is defined by the power series analogously to the scalar exponential function
In order to be able to specify a closed expression here, it is helpful to transform to diagonal form using the principal axis transformation. For a diagonal matrix of the form
the matrix exponential function then results
Normal forms
Normal forms are used to clearly emphasize the structural properties of a system. In the state space representation, a system often has state variables which are not noticeable in the transmission behavior of the system. So it can be B. be that poles and zeros are shortened so that they have no influence on the transfer function . This case is called a non-minimal implementation of the system, and this means that the system is either not controllable, not observable, or neither controllable nor observable.
Normal control form
The given transfer function can be converted into a state space representation using the following approach.
The given transfer function is multiplied into the numerator and denominator factors
- .
The differential equation (DGL) belongs to this transfer function in the frequency domain in the time domain:
This DGL results in the following equations of state for the ZR representation according to the normal control form:
The coefficients can now simply be entered directly into the state matrices:
In general:
For systems that cannot jump:
The transformation matrix follows from the controllability matrix
.
If the system is controllable. Then off
the transformation matrix
are formed.
Observation normal form
The differential equation after solved
and 4 times integrated results
- .
The state variables can be derived from this
and the output equation
derive. Insertion of results
- .
or in matrix form
The transformation matrix follows from the observability matrix
If the system is observable. Then off
the transformation matrix
are formed.
Canonical normal form
If the transfer function has simple, real poles , a partial fraction decomposition of the form
be performed. Out
the equations of state result from the inverse transformation
and the output size
- .
In matrix notation:
and
The equations of state are decoupled in this case. The transformation matrix is written in the form from the eigenvectors belonging to the eigenvalues of the system matrix
literature
- Serge Zacher, Manfred Reuter: Control technology for engineers: Analysis, simulation and design of control loops . 14th edition. Springer Vieweg Verlag, Wiesbaden 2014, ISBN 978-3-8348-1786-0 .
- Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Europa-Lehrmittel, Haan-Gruiten 2019, ISBN 978-3-8085-5869-0 .
- Jan Lunze : Control engineering 1: System theory basics, analysis and design of single-loop controls . 10th edition. Springer Verlag, 2014, ISBN 978-3-540-68907-2 .
- Jan Lunze: Control engineering 2: multi-variable systems. Digital control (with MATLAB) . 8th edition. Springer Verlag, 2014, ISBN 978-3-642-53943-5 .
- Heinz Unbehauen : Control engineering I: Classical methods for the analysis and synthesis of linear continuous control systems, fuzzy control systems . 15th edition. Vieweg & Teubner, 2008, ISBN 978-3-8348-0497-6 .
- Gerd Schulz : Control technology 2: multi-variable control, digital control technology, fuzzy control . 2nd Edition. Oldenbourg, 2008, ISBN 978-3-486-58318-2 .
- Gerd Schulz: Control engineering 1: linear and non-linear control, computer-aided controller design . 3. Edition. Oldenbourg, 2007, ISBN 978-3-486-58317-5 .
- Heinz Unbehauen: Control engineering II . Friedr. Vieweg & Sohn, 1997, ISBN 3-528-63348-4 .
- Günter Ludyk: Theoretical control engineering 1 . Springer Verlag, Berlin 1995, ISBN 978-3-540-55041-9 (basics, synthesis of linear control systems).
- Theoretical control engineering 2 . Springer Verlag, Berlin 1995, ISBN 978-3-528-08911-5 (state reconstruction, optimal and non-linear control systems).
- Ulrich Korn , Hans-Helmut Wilfert: Multi-variable regulations - modern design principles in the time and frequency domain . Verlag Technik, Berlin and Springer-Verlag, Vienna; New York, 1982, ISBN 3-211-95802-9 .
Individual evidence
- ↑ Heinz Unbehauen : Control Systems I . 15th edition. Vieweg + Teubner, 2008, ISBN 978-3-8348-0497-6 , pp. 49 ( limited preview in Google Book search).
- ↑ a b Description of dynamic systems in the state space. In: Oliver Nelles: Lecture manuscript for measurement and control technology II. University of Siegen, May 4, 2010.
- ↑ Torsten Wey: Nonlinear control systems: a differential algebraic approach . Springer-Verlag, 2002, p. 291 ( limited preview in Google Book search).
- ↑ State space representation of linear systems. In: Jan Lunze: Control engineering I.
- ↑ Equations of state of single-variable systems. In: Gerd Schulz: Control engineering 2.
- ↑ Controllability and observability, normal forms , Chapter 3. In: Gerd Schulz: Regelstechnik 2
- ↑ State controller through pole specification. In: Oliver Nelles: Lecture manuscript for measurement and control technology II. University of Siegen, May 4, 2010.
- ^ A b Lunze, Jan .: Control engineering 1: System-theoretical basics, analysis and design of single-loop controls . Springer-Verlag Berlin Heidelberg, Berlin, Heidelberg 2010, ISBN 978-3-642-13808-9 , pp. 153 f .
- ↑ Adamy, Jürgen 1962-: System dynamics and control engineering 2 . 6th edition. tape 2 . Düren, ISBN 978-3-8440-6631-9 .
























































































































![{\ displaystyle Q_ {S} = {\ bigg [} \ B \ | \ AB \ | \ A ^ {2} B \ | ... | \ A ^ {n-1} B \ {\ bigg]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4851c94bad0b5d3f4b259bf0cfc71ce88c246b27)