Controlled system

In control engineering, the term “ controlled system ” refers to that part of a control loop that contains the physical variable to be controlled - the controlled variable - on which the controller is to act via the manipulated variable . Known controlled variables are z. B. room temperature, level of a container, position of a mechanism.
As a dynamic system, the controlled system can consist of a chain of mostly unknown individual systems, the output variable of which is measured by a measuring element and fed back to the controller via a set-actual value comparison. The actuator as the interface between the controller and the controlled system can be part of the controlled system, the controller or an independent device. A control system becomes a controlled system when it is included in a control loop .
Mathematically, the controlled system is defined as a transmission system. It can consist of one or more transmission systems and of single-variable and multi-variable systems ( MIMO ). The transmission systems can have linear and non-linear behavior. Accordingly, the mathematical descriptions of the controlled system are different.
Linear transmission systems ( linear time-invariant system ) can be described by differential equations , by transfer functions , by numerical time-discrete methods ( difference equations ) and in the state space .
Non-linear transmission systems such as signal limitations and systems with non-linear characteristics can be described in the form of tables ( matrices ) with numerical discrete-time methods (see Numerical discrete-time methods ) or in the state space representation. Dead time systems can be described with the complex frequency or calculated using numerical time-discrete methods.
In order to be able to design the controller for demanding control tasks, it is necessary to identify the controlled system. This is done by creating a mathematical model of the controlled system that is intended to reproduce the behavior of the controlled system over time as precisely as possible. If the model cannot be calculated, the control system can be excited by a suitable test signal and the output signal recorded as an identification method (see Identification of the controlled system). The temporal behavior of these signals allows identification to a plant model.
Characterization of the controlled systems
The general form of a differential equation for a linear time-invariant transfer element ( linear time-invariant system ) with the input variable and the output variable and constant coefficients is:
The highest degree of derivation of gives the number of system memory elements in the route.
All input signals are assumed to disappear for. This means that the one-sided Laplace integral can be used. With the help of the Laplace transformation, a time function can be assigned to an image function .
For the transformation from the time domain to the s domain, there are several theorems such as the shift theorem, the damping theorem, the differentiation theorem, the integration theorem, the convolution theorem, and limit theorems. These Laplace theorems are described in every textbook on control engineering.
Application of the transfer function
If the differential equation of a transmission system is transformed into the s-domain (also image domain) by means of the Laplace differentiation theorem, the general form of the transfer function arises as a rationally broken function in polynomial representation.
The transfer function is defined as the ratio of the output signal to the input signal of a system as a function of the complex frequency :
If all derivatives and associated coefficients are present in the polynomial representation without gaps with a positive sign, the transfer function for the exponents represents a time-delaying asymptotically stable system.
There are several ways that lead to a transfer function :
- Laplace transformation of the system-describing ordinary differential equation,
- from the signal ratio , if this is known,
- by measuring the frequency response ,
- Voltage divider from a reaction-free impedance ratio (example: RC-wired operational amplifier),
- through system identification using step or impulse response.
The transfer function is an abstract, non-measurable quantity and describes the mathematical behavior of a linear time-invariant system in the frequency domain with the complex variable . After decomposing numerator and denominator polynomials by determining zeros into product terms (linear factors), it is successfully used for system analysis, system synthesis, system stability and allows the algebraic treatment of arbitrarily switched, reaction-free subsystems. The position of the zeros and poles of a transfer function in the s-plane in the pole-zero diagram is one of the most important criteria for determining the stability of a system.
The transmission systems defined in the complex frequency range (s range) have the following meanings:
- is the independent variable in the complex frequency domain (image area, s-area) with as real part and as imaginary part. It allows any algebraic operations in the s-domain, but is only a symbol for a completed Laplace transformation and does not contain a numerical value. Exponents of s correspond to the degree of derivative of the differentials .
- Numerical values arise from the coefficients of and its powers, in that the polynomials of the s-transfer function are broken down into linear factors (products) by decomposing zeros. These zeros or poles can be zero, real or conjugate complex.
- In the time constant representation of the linear factors, the time constant as a dimensionless number after the inverse transformation determines the time behavior of a subsystem in the time domain.
- If the basic terms (coefficients) or the transfer function are missing , the linear factor is used . The variable can be released from the polynomial and, depending on its position in the numerator or denominator, means a global differentiating or integrating system behavior in the time domain.
- Second degree linear factors with complex conjugate poles or zeros are combined into quadratic terms in which only real coefficients occur for easier calculation.
- The numerator order of the transfer function must not be greater than the denominator order. It applies with initial conditions assumed to be zero.
Factoring the transfer function in the s domain
By determining the zeros , the polynomials of the transfer function can be brought into a product form ( linear factors ) in the numerator and denominator. The poles (zeros of the denominator) or zeros (zeros of the numerator) are either zero, real or conjugate complex . The product representation in the numerator and denominator of the transfer function is mathematically identical to the polynomial representation in the numerator and denominator.
Ready-made programs for determining the zeros of a polynomial up to the 4th order can be found on the Internet under the call "Determine zeros (solutions) of polynomials". For systems of the 2nd order, the “pq formula”: can be used to calculate the conjugate complex zeros.
Linear factors of the pole zero representation
Example of the decomposition of the polynomials of the transfer function by determining the pole zero position into real linear factors:
Since the linear factors of the numerator and denominator of the transfer function are identical, the zeros and poles are denoted by for a simplified representation . Negative real parts of the poles and zeros of the linear factors mean stable elementary systems, positive real parts mean unstable elementary systems.
With the linear factors for real poles and zeros, the negative numerical values are set equal : Zero (negative numerical value).
In the case of the linear factors for systems of the 2nd order with real complex conjugate poles and zeros, the numerical values have the form: with a = real part, imaginary parts.
If numerical values of the polynomials of the transfer function are available, the following forms of linear factors can arise with the determination of the zeros:
- with missing absolute terms (coefficients) of the transfer function:
- with real poles and zeros:
- = Real part.
- for systems of the 2nd order with conjugate complex poles and zeros:
- = Real part, = imaginary parts.
- These linear factors are combined into quadratic terms in which only real coefficients occur for easier calculation.
- .
Linear factors of the time constant representation
The linear factors of the pole-zero representation can also be defined as a time constant representation in which the numerical values of the poles or zeros are defined as quotients . ( )
- The linear factor of the 1st order becomes in the time constant representation:
- where all terms are positive.
- One factor takes into account that the pole-zero representation and the time constant representation must be mathematically identical.
- From the quadratic linear factor of the 2nd order, the normal form applies in the time constant representation:
- with D = degree of damping.
The factored time constant representation is common and more descriptive. All terms of the transfer function are always positive in stable systems.
The linear factors in the denominator of the transfer function determine the time behavior of the subsystem for a given input signal . The linear factors in the counter only have an influence on the size of the amplitude of the output signal .
In linear control technology, all transmission elements can be composed of the following three basic forms. They have a completely different meaning, whether they are in the numerator or in the denominator of a transfer function. They also differ in whether they are regular or the rarely naturally occurring non-regular systems.
The linear factors with negative real parts of the poles and zeros characterize the following stable elementary systems:
| Type linear factor pole-zero representation |
Type linear factor time constant representation |
Meaning in the counter | Meaning in the denominator |
|---|---|---|---|
|
Absolute term a 0 or b 0 is missing, |
Zero or pole |
Differentiator, D-member | Integrator, I-link |
|
; real zero |
With |
-Element | Delay, -link |
| Quadratic linear factor: with |
Normal form: with |
Term for 0 < D <1 with conjugate complex zeros. Application: prefilter of the reference variable |
Vibration link , link for 0 < D <1 with conjugate complex poles.
|
- Here is the time constant, the complex frequency, the degree of damping.
If the numerical values of the poles and zeros are positive, the following unstable transmission systems result in the time constant representation:
| Type linear factor time constant representation |
Meaning in the counter | Meaning in the denominator |
|---|---|---|
| Non-regular system of the first order |
Unstable transfer element with positive zero point (no technical significance) |
Unstable, irregular transmission link with a positive pole. Monotonically increasing amplitude as a transition function. |
| Non-regular system of the 2nd order |
Unstable 2nd order transfer element with a negative and positive zero (no technical significance) |
Unstable vibrating element with a negative and a positive pole. As a transition function, monotonically increasing vibration amplitude. |
These non-regular linear factors have a non-linear input-output behavior and can be understood as mathematical models of positive feedback as hysteresis effects. The non-regular linear factors can be calculated algebraically in combination with regular linear factors. The same non-regular subsystems with the same time constants must not be abbreviated from the numerator and denominator of a transfer function. Control loops with a non-regular subsystem of the controlled system can become stable without any problems with suitable controller parameterization.
Tabular representation of the system behavior of 1st and 2nd order linear factors in the denominator of the transfer function
| Name → | PT1 element | I-link limit stable |
Instab. T1 element monotonous instab. |
PT2 KK link oscillatory damped |
PT2 KK -link oscillate. borderline stable |
Instab. T2 KK- member oscillatory unstable |
|---|---|---|---|---|---|---|
| Transition function → (step response) diagrams calculated numerically [s] |
||||||
| Poles → | ||||||
| Transfer function → as step response |
Partial fraction representation
With the correspondence table of the Laplace transformation found in every textbook on control engineering, terms of the transfer function of the product representation can be transferred to the time domain . For transfer functions not dealt with in the correspondence tables, the transfer functions of the product representation can be broken down into additive terms by means of partial fraction decomposition, the simple time functions of which are known.
To do this, the denominator polynomial N (s) of a transfer function G (s) must be factored in the following form. The poles of the transfer function determine the partial fractions:
Partial fraction representation for real poles and zeros with an absolute term:
- The unknown parameters can be determined by comparing coefficients.
A product term of a simple delay element of a transfer function with the pole can be transferred directly to the time domain:
- (Impulse response)
For transfer functions with the various forms of the linear factors, the calculation of the partial fractions can be complex.
The calculation of the output signal of a dynamic system with a given input signal is fundamentally easier if the linear factors are converted into difference equations and these are solved numerically.
Frequency response
The frequency response is a special case of the transfer function. It characterizes the behavior of a system with forced continuous oscillation and the imaginary frequency . Frequency response and transfer function differ only in the way they arise.
All forms of linear factors (here in time constant representation):
of the numerator and the denominator can without loss of information as a frequency response with graphically in the Bode diagram, or as the frequency response of locus are displayed and are used to viewing and stability of the system analysis.
Switching of control loop elements
Transmission elements can be interconnected as:
- Series connection:
- The principle of undisturbed superposition applies. The systems in product presentation can be in the order z. B. can be moved arbitrarily within an open control loop.
- The superposition principle for the open control loop does not apply if
- Limitations take effect within the controlled system (non-linear behavior)
- within the controller - which happens very often - limitations act (non-linear behavior)
- the point of attack of a disturbance e.g. B. is at the entrance of the controlled system. (Reason: The counters of the disturbance transfer functions when a component of the controller is shifted before or after the point of application of the disturbance variable are not identical)
- Parallel connection: ,
- Negative and positive feedback:
The factorial representation of the basic elements in the series connection is very advantageous because all data for the criteria of stability such as poles, zeros, gain and time constants can be derived from the transfer functions of the control loop elements. The same differentiating and delaying basic forms of the transfer functions with the same time constants compensate each other to G (s) = 1.
Types of controlled systems
A distinction is made between linear controlled systems and non-linear controlled systems . In the case of linear controlled systems, a distinction is made between controlled systems with compensation , without compensation and unstable controlled systems .
- In the case of controlled system elements with compensation, the output variable y (t) reaches the input variable u (t) after a sufficiently long time. Both sizes are different for only by the proportionality factor K. .
- Linear controlled system elements without compensation are controlled systems with I behavior (I element). The output variable y (t) with a stepped input variable u (t) strives for an infinitely large value after a sufficiently long time.
- Formally, these controlled systems with an I element are therefore stable to the limit, the value of the output variable remains stored when the input variable u (t) becomes zero.
- An I-element fulfills the concept of "internal stability", but is not "externally stable" because its output variable increases without restriction for a given input variable.
- Unstable control systems can be recognized by the type of pole. They lie in the right half-plane and have a positive real part. The transfer function in the product representation has a negative coefficient. The polynomial of the characteristic equation of the transfer function can contain positive poles despite positive coefficients and thus be unstable.
Linear controlled systems
P controlled system
The output of a P element is proportional to the input. A voltage divider or the reductions in hydraulic systems are examples of P-controlled systems.
1st order delay element (PT1 element)
The PT1 element occurs most frequently in nature and in technology. It arises z. B. when heat flows into a medium or voltage is applied to an RC element. The PT1 element is a balanced system.
Differential equation:
Transfer function:
See also Bode diagram and locus curve of the frequency response under PT1 element !
2nd order delay element (PT2 element)
If a denominator polynomial of normal form can be resolved into factors with the help of the formula for solving mixed quadratic equations, two PT1 elements are created in series. The PT2 element is a balanced system.
Differential equation:
Transfer function:
If the denominator polynomial of the above form for the damping D has a value 0 <D <1, the system has conjugate complex poles. This form of the PT2 element is called an oscillating element:
Transfer function:
Oscillating elements are created by exchanging energy between two storable delay elements of the 1st order, such as spring-mass systems, LC oscillating circuit.
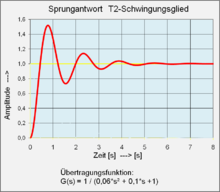
The graphic shows the step response of a vibrational link with the transfer function:
- , the degree of damping is D = 0.22
See also Bode diagram and locus curve of the frequency response under PT2 element !
Integrating transfer element (I element)
A typical example of an I-element is the inflow of a liquid into a container or the charging of a capacitor with an adjustable constant current.
The I-element is a system without compensation; the output variable increases monotonically as a function of any constant input variable.
Because of the position of the pole in the s-plane, it is also called border-stable.
It differs from a PT1 element in that it is the coefficient in the linear differential equation .
The general differential equation:
becomes for the I-link to:
Transfer function with , reset time :
See also Bode diagram and locus curve of the frequency response under I element !
Unstable control systems
Unstable control systems can arise B. by:
- two or more I-links connected in series
- Feedback in the function plan (action plan) of the route. Is z. If, for example, the output signal of a positive amplifying I element is fed back to the input with a positive sign, an unstable transmission element of the first order is created.
They can arise in nature when acceleration forces act on the position of bodies, such as those caused by e.g. B. caused by gravity or magnetism, then the situation is increasingly accelerated. The output variable y (t) grows progressively up to a natural limit.
The stabilization of such routes is of increasing importance in industry. In the specialist literature, calculation examples for unstable control systems are presented more and more frequently. Applications are inverse pendulum (transport of an upright rocket on the wagon, loading bridge on a ship or freight train), "magnetic float" (positioning when approaching a magnetic levitation train). Often these unstable control systems also have non-linear components, for example in chemical reactors with exothermic reactions.
1st order unstable transfer element
This transmission link is sometimes referred to colloquially as an 'unstable PT1 link'. However, this designation is formally incorrect, since there can be no proportional behavior with an unstable transmission element because the output variable does not adjust to a final value.
The differential equation with a negative coefficient is e.g. B .:
The transfer function is:
The step answer is:
The time behavior of an unstable element of the 1st order with a test signal is described as follows:
- A pulse function or a step function of any amplitude immediately starts the output signal, which increases exponentially up to a natural limit.
- Within the working range, the output signal can only be started in the opposite negative direction if a negative input signal - a step function - is greater than the current positive value of the impulse or step response. This is explained by the principle of positive feedback.
- If the negative step function is present so long that the step response is also negative, the step function can become zero. The step response then continues independently until it is limited in the negative direction.
This controlled system is relatively easy to regulate with a PI controller.
Unstable 2nd order transfer element
If there are negative coefficients in the denominator of a 2nd order transfer element, or the attenuation is D = 0, the system is unstable. If there are complex conjugate poles, the system oscillates with increasing amplitude. If the numerator of the transfer function does not contain a power of s higher than the 0th order, it is often referred to as an 'unstable PT2 member' due to the similarity of the transfer function to a PT2 member. Formally, however, this designation is incorrect, since the output variable of the unstable transfer element of the first order does not converge towards a finite value, i.e. it cannot exhibit any proportional behavior.
If the transfer function of an unstable transfer element of the 2nd order is z. B .:
If the denominator polynomial of the transfer function has no complex conjugate poles, i.e. H. the attenuation is D , then the polynomial can be broken down into a PT1 element and an unstable transmission element of the first order or into two unstable transmission elements of the first order. E.g.
The same result is obtained for the transfer function when T1 = T2 = T for
This unstable controlled system is also relatively easy to control with a PID controller.
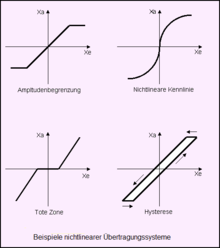
Non-linear transmission systems
In linear transmission systems , the output variable in the steady state is always proportional to the input variable. In the case of non-linear systems, at least one non-linear function acts in conjunction with linear systems. These non-linear functions are differentiated according to continuous and discontinuous non-linearities. They can be used as signal or manipulated variable limits, as continuous non-linearity e.g. B. with quadratic behavior, as functions with limited response sensitivity (dead zone) for sensors and / or with hysteresis. Theoretical studies of the stability of control loops with non-linearities can be very complex. To make it easier to determine the dynamic behavior and stability of a control loop, a certain area around the operating point of a non-linear transmission system can be considered. If the dynamic deviations exceed the selected operating point, the entire non-linearity must be included in the calculation.
One of the analytical methods that can be used is harmonic balance . With the equation of the harmonic balance , the relationships of the descriptive function of the static non-linear system and the dynamic linear system are put into a relationship. From this, the two critical system variables of the harmonically oscillating control loop - the input amplitude and the critical frequency at the stability limit - can be calculated or determined graphically using the two-locus method.
According to the specialist literature, up to 40 different description functions of non-linear static systems can be taken.
Dead time element
The dead time element is a transmission element that occurs frequently in practice and usually works in conjunction with other delay elements. It is caused by the pure transit time or transport time of a signal. It behaves like a P element whose output variable arrives late by the dead time without distorting the input variable during this time. Any change in the input variable is delayed by the dead time at the output.
Time behavior:
Step response:
- ,
- .
Transfer function:
See article dead time (control technology)
Signal and manipulated variable limitation (saturation)
Signal limiting functions are the most common elements among non-linear systems. A valve can only be 100% open and an electric motor must not be operated at its maximum output.
The limiting effects of the controller and, more rarely, those of the system must be coordinated with one another with regard to the control dynamics. The output variable of the controller (manipulated variable) must not be larger than the input variable that the controlled system can process.
In general, a signal variable limitation or manipulated variable limitation has a dampening effect on the large-signal behavior of the subsequent system or control loop. The time course of the controlled variable slows down. Algebraic calculations with transfer functions are not valid for mixed linear and nonlinear single systems.
If the transfer functions of the individual linear systems of the controlled system are known through a system analysis, the effect of the non-linear limiting function can be clearly illustrated for the control loop by means of a numerical simulation of the controller and the system. Difference equations and logical functions are used to simulate the behavior over time of linear and non-linear transfer elements.
See article difference equation
Non-linear continuous characteristic of a controlled system
The quadratic characteristic of a spring characteristic or the non-linear change in cross-section of a valve mean different system gains in control systems that otherwise operate with linear systems. If a control loop is set for a fixed setpoint, the manipulated variable has a certain working range within the non-linear function. By applying a tangent to the working area of the non-linear function of the controlled system, the gain of the linearized partial characteristic can be determined. With the gain from the quotient of the tangent at this operating point, the behavior of the control loop can be calculated if the transfer functions of the other transfer systems are known.
If any setpoints are to be set for a given control loop, the parameters of the controller must be optimized for the greatest amplification of the non-linearity of the system, otherwise there is a risk of instability of the control loop with increasing system gain. At the same time, this is associated with poor dynamic behavior of the control loop if the non-linearity around the operating point has a lower gain.
A compensation function (inverse non-linearity) in the input of the non-linear system can help. For a digital controller, this would only be a table that must be taken into account so that the non-linearity can be converted into a linear function with proportional behavior. The compensation function is not subject to the superposition principle.
Discontinuous response sensitivity (dead zone)
Play occurs in mechanical systems in particular , so that a certain input variable must first be exceeded before the output variable changes. For a control loop, this means that small control deviations cannot be adjusted or the system becomes unstable.
Hysteresis
By friction on valves, by magnetic effects e.g. B. with relays or through coupling to operational amplifiers, the hysteresis effect can occur. The hysteresis can have constant or discontinuous behavior. The hysteresis function is desirable for unsteady controllers. The hysteresis effect is very undesirable for continuous regulation.
Test signals
The non-periodic (deterministic) test signals are of central importance in control engineering . With their help it is possible to test a transmission system, check it for stability or determine properties.
The test signals have in common that they begin at time t = 0 and have an amplitude = 0 at t <0. The test signal is shown as input variable u (t) in a transmission system and the system response as output variable y (t) in the table below. To distinguish the function of the signals, they are indicated with the characters δ ( pulse ), Ϭ ( jump ), a ( rise ) and s ( sine ).
The theoretical delta pulse (δ pulse, Dirac pulse) for t = 0 with an infinitely large amplitude is not technically feasible. A square pulse with the pulse area 1 = amplitude · time is defined in its place. In practice, a value for the pulse duration of Δt = 1% to 10% of the dominant time constant of the transmission system to be tested is sufficient.
System response Xa (s) and Xa (t) of the test signals: The test signals in the image area can be multiplied by a transfer function of a system. The response of the test signal for the transmission system is presented during the back transformation into the time domain. If a digital computer is to be used to solve the system response using numerical methods, the continuous time variable t for the non-periodic test signals Xe can be converted into a sequence of n time steps (discretization time = Dt) can be replaced by t = n · Dt.
The system response of an impulse function Xaδ (t) in the time domain represents the behavior of the system. The reverse transformation of any transfer function f (s) into the time domain f (t) always also the impulse response of the system.
The differentiation of the step function corresponds to the impulse function. The integration of a step function corresponds to the increase function. The differentiation of the step response of a transmission system corresponds to the impulse response.
The sine function belongs to the group of periodic signals. The frequency-variable feed of a transmission system allows the amplitude and phase response of the system to be recorded. The transfer function of the system can be determined with the help of the Bode diagram.
| Term test signal u (t) |
Time behavior of the test signal | Image area | System response y (t) |
|---|---|---|---|
Impulse function δ or impact function, delta impulse |
Normalized pulse = pulse duration = main application: recognition of the system, order and stability
|
Impulse response or weight function |
|
| Step function σ |
Unit jump: Main application: Recognition of the system |
|
Step response or transition function |
| Increase function or ramp |
Slope function: Gradient: Main application: Determination of the tracking properties |
Rise response or ramp response |
|
| Sine function s |
Main application: recording the amplitude and phase response of a system |
|
Frequency response |
Experimental system identification of controlled systems according to the step response
1st order systems
Simple controlled systems that are described by a first-order system can be easily identified by the step response of the system. The graphic images in the "Linear controlled systems" section apply.
1st order delay element (PT1 element)
The transition function for already shows a vanishingly small initial value y (t) for a vanishingly small time value t.
In contrast to the transition function of delays of the 2nd or higher order, the output variable y (t) for a vanishingly small time value t is always y (t) = 0. This behavior can be observed particularly well with the impulse responses of several PT1 elements connected in series (→ see graphic under test signals chapter ).
The function y (t) asymptotically approaches the maximum of the physical variable Y_max. The time constant T corresponds to the time value of t, which is formed by 63% of y_max as the intersection in the function of the step response. The proportionality factor of the distance Ks (t) is determined from y / u in the steady state.
Transfer function:
Integral controlled system (I element)
The step response - assuming the system's memory is empty - forms a monotonically rising straight line that starts at the origin of the coordinate system and ends only through natural limits. The route coefficient results from .
Transfer function:
Combinations of PT1 element and I element
Above the steady state (steady state) of the PT1 system, an auxiliary line can be drawn directly to the origin by parallel displacement and shows the behavior of the I element. A horizontal line of a value in the steady state of y intersects the two characteristics. The horizontal distance between these intersection points corresponds to the time constant T of the PT1 element. The characteristic values of the I-element are calculated as already defined.
Transfer function:
1st order unstable transfer element
The time constant can be read directly from the step response. The following applies to the jump :
The value of intersects the function of the step response in the horizontal direction. The time associated with this point - the intersection line in the vertical direction - is equal to the time constant .
Transfer function:
Higher order systems
PT2 vibrating link
If the step response of this system is given graphically, the transfer function of the oscillating element can be calculated from the amplitude ratio of the first two half-waves.
First the vibration damping is calculated:
The time constant T is calculated from the period Te of the 1st oscillation and from the damping D:
This gives the transfer function:
Non-vibrating systems of higher order
There are a number of Ziegler-Nichols method , with landscaped tangent at the inflection point of the function determine an approximation of the step response function from the step response of the controlled system.
Time percentage value method (black)
With the method of the "time-percentage value method", for example, a model route is determined that actually offers a very good approximation of the real step response with the same time constants depending on the route constants of any order (Zeitschrift Automatisierungstechnik, Munich 1993 by Latzel).
For a given step response of a non-oscillating controlled system, the associated time values T10, T50 and T90 are recorded from the amplitude values Xa of 10%, 50% and 90% of the maximum amplitude in the steady state, and a model transfer function is formed from n equal delay elements.
The following steps are required:
- The order of the plant model is determined from the ratio μ = T10 / T90 using a table.
- Factors α10, α50 and α90 are read from the same table.
- The same delay time Tm for the model route for each order is calculated as follows:
This establishes the order of the model system and the same time constant for each order.
In another table (according to Latzel), the controller parameters for various standard controllers in a parallel structure can be read off for the model transfer function determined .
The tables of this procedure are contained in every good technical book on control engineering , e.g. B .:
- Gerd Schulz: Control engineering 1. Oldenbourg Verlag, Munich, 3rd edition 2004.
- Manfred Reuter, Serge Zacher: Control technology for engineers. Vieweg Verlag, Braunschweig, 11th edition 2003.
The process was developed by Gunter Schwarze in the early 1960s. It avoids the uncertainties of tangent methods . He laid out the theoretical basis for this in his habilitation thesis .
Experimental system identification through variable-frequency feed into the controlled system
If the Bode diagram of an unknown higher-order controlled system is available, the system constants can be determined by entering the asymptotes in the amplitude response. If the controlled system also contains a dead time, the phase response of the controlled system is also required.
The Bode diagram and the system constants are determined as follows:
- Define the operating point of the controlled system, e.g. B. to 50% of the work area.
- Additively feed a sinusoidal variable frequency with the greatest possible constant amplitude to the operating point so that no limiting effects occur at the output of the controlled system. The frequency is adjusted in steps so that the output amplitude changes from undamped to less than 1%.
- The z. B. the input amplitude normalized to the value 1, the output amplitude and the phase shift of the output amplitude are tabulated as a function of the frequency. The amplitude ratio is entered in the Bode diagram on a logarithmic scale as the amplitude response. With the phase response, the phase is entered on a linear scale.
- After drawing in the asymptotes (20 dB / decade for a PT1 element), the corner frequencies can be determined. The phase response is used to check whether the sum of the number of time constants (or the order of the system) matches the sum of the phase shift (PT1 element 90 ° / decade).
- If the corner frequencies are close together, they cannot be determined as precisely. In this case it is advisable to create a new Bode diagram with the found transfer function and to compare the two amplitude responses for congruence and, if necessary, to correct the transfer function determined previously.
Experimental identification of a controlled system with the help of a model controlled system
A controlled system can be identified by the step response, by the impulse response of the controlled system or by feeding in a variable frequency.
The most important features for the application of a model controlled system using the step or impulse response are:
- The parameters of a controlled system can be determined by means of a simple model controlled system in that the characteristic curve of the model is adapted to the characteristic curve of the unknown controlled system by gradually changing the time constants of the model.
- The model must have similar system properties as the unknown controlled system.
- In the case of routes without compensation, the model requires an I component; for routes with dead time, a dead time element is also required for the model.
- The adaptation of a model to the unknown controlled system with the help of the step response is relatively easy and can possibly also be carried out graphically.
- The adaptation of a model to the unknown controlled system with the help of the impulse response is somewhat more complex, but if the characteristic curves are congruent, it offers complete correspondence between the original and the model in a control loop in comparison with the respective step responses. This model can also be used to determine the order of the original.
- It should be easy to do.
Identification of a controlled system with compensation and dead time through the step response
The step response has the advantage that it is easier to carry out and that the expected result is better known. The time-independent system gain Ks can be read off directly in controlled systems with compensation in the static state.
The following requirements are placed on the model controlled system for a controlled system with compensation:
- The step response of the model controlled system should be largely congruent with the original controlled system.
- The model controlled system should have a certain form of the transfer function which is easily suitable for parameterizing the controller with a good linear standard controller - for example a PID controller.
- The method should be applicable for controlled systems from the 2nd order with and without dead time.
A PID controller in the product representation (series connection) can compensate for 2 PT1 delays. Therefore, the following form of the model controlled system, which is easy to determine and consists of a vibration-free PT2 element and a dead time element, is selected:
- Transfer function model:
Ttv consists of any dead time Tt that may be present and the shift time caused by the graphic construction or by a simulation program.
- The step response of the PT2 element is:
Procedure for determining the model controlled system:
The construction of the model can be carried out graphically in the recorded diagram of the step response of the unknown controlled system.
The course of the PT2 element is much simpler to design using a simulation program if the original function is entered in the computer program using a suitable number of measuring points. The procedure for the graphic process and for the use of a simulation program is identical in both cases. For the construction of the model, the characteristic curve of the PT2 element in the middle amplitude range of the original is adjusted to the slope of the characteristic curve of the original by gradually changing the two time constants T. The coincidence of the two characteristics is achieved by horizontally shifting the characteristic of the PT2 element - if a simulation program is available by a dead time element - to the characteristic of the original. Then the fine adjustment takes place with the time constant T and the shift time (Ttv). If the two characteristics are congruent, the time constants of the model can be read off with Ttv and T.
If the dead time of the original route is not greater than 50% of the dominant time constant, a PID controller can be optimally parameterized with guidance properties in the product representation using the data determined from the models Ks, Ttv and T according to the following rules:
- Pole-zero compensation: Tv1 = T, Tv2 = T,
- Reinforcement:
- The route gain Ks results from the ratio of y / u of the original route in the static state.
- Result: The step response of the control loop contains approx. 5% to 10% overshoots with the degree of damping D approx.> 0.5
See under parameterization of a PID controller: "Example: PID controller structure for a controlled system with two delays and one dead time".
The corresponding graphic shows the good congruence of the characteristic curves of the step responses of the model and the original. The parameters found for the model are well suited for parameterizing a PID controller.
Error consideration of the step response of the model to the step response of the original function:
For higher-order systems with any time constants and dead time element, the application of the proposed model is relatively accurate with respect to the step responses of the two systems with an expected amplitude error of 0.5% to 1%. Only in the case of a non-realistic controlled system, where z. If, for example, four similar or equal time constants occur, a system-related error of 3% can occur - provided that the two characteristics are carefully adjusted. The error in the step response of a control loop that contains the original system or the model with otherwise identical controller settings is of course greater.
Identification of a controlled system with compensation and dead time through the impulse response (weight function)
The pulse function can be defined by a standardized pulse. The pulse width of the product should be very small compared to the time constants of the transmission system. In practice, a value of 1% to 10% of the dominant time constant of the transmission system to be tested is sufficient . The amplitude of y resulting from this relationship must be checked for possible limiting effects of the transmission system, otherwise there will be errors in the impulse response.
Model for a controlled system using the impulse response
Analogous to the model example with the step response, a model with three delays with the following transfer function is proposed:
If there is a dead time in the original function, the model must be expanded to include a dead time element. In contrast to the model with the step response, a PT2 element and a dead time element cannot match the characteristics of the impulse responses of the original and the model, because the characteristic of the impulse response is more sensitive to mismatching.
The experimental parameterization of the model is carried out step by step by changing the time constants, whereby first the peak value of the impulse response of the model and then the entire characteristic curve with the same peak value is brought to coincide with the characteristic curve of the unknown impulse response.
When constructing the characteristic curve coverage with the same peak value of the impulse responses, the following is noticeable:
- One or all of the time constants of the model must be reduced if the characteristic of the model lies to the right of the symmetry axis of the vertex of the original. Otherwise, the order of the model will be higher than the original.
- If the characteristic curve of the impulse response lies to the left of the axis of symmetry of the peak value of the original, an additional delay would have to be included in the model if one would like to achieve congruence of both characteristic curves.
This model is difficult to create graphically. It is recommended to use a simulation program for the three PT1 elements.
The associated graphic of the impulse responses of the original and the model does not show a complete match between the two characteristics, because the original contains 4th order time delays. Nevertheless, the model determined is at least as accurate as the model determined with the step response.
Comparison of the quality of the models with the step response and the impulse response
The impulse response of a transmission system is identical to the differentiation of the step response of the system. Therefore, the middle area around the turning point of the characteristic curve of the step response is greatly enlarged by the differentiation. The procedure with the comparison of the characteristic curves of the impulse responses of a system model and the original allows a more precise identification of the system than with the comparison of the step responses. The only way to prove this is by simulating both processes in one control loop.
Stability of the controlled system elements
If all the coefficients of the differential equation from the highest derivative from to are completely positive and positive for a transmission system , then a basic requirement of the stability of the system is first met.
A linear time-invariant transmission system is asymptotically stable (also called internally stable) if its impulse response (weight function) decays asymptotically after a sufficiently long time. If, on the other hand, the impulse response increases against a natural limit stop after a sufficiently long time, the system is unstable.
As a special case, there are systems that, according to the impulse response, increase with increasing time, but do not exceed a finite limit value. These systems, also referred to as borderline stable, concern z. B. the I-member or the T2-vibrating member.
Internal stability
Internal stability means that every link in the controlled system is stable. A transfer system is internally stable if the transfer function only has poles in the left half-plane:
External stability ( BIBO stability )
In contrast to internal stability, it relates to the overall system of the control loop. A transmission system is considered to be externally stable if a limited input signal to the system also causes a limited output signal. Individual elements of the control loop can be unstable as long as the entire control loop exhibits stable behavior.
A controlled system is unstable
- if the output variable oscillates continuously,
- if the output variable oscillates with increasing amplitudes,
- when the output size increases progressively beyond all limits.
Consideration of stability through the position of the poles
To recognize the stability of a transfer function, it is sufficient to consider the position of the poles in the s-plane (ordinate with Ϭ, abscissa with j * ω):
- Asymptotic stability: all poles must lie in the left half-plane,
- Instability: if at least one pole lies in the right s-half plane or if a multiple pole lies on the imaginary axis of the s-plane.
- Borderline stable: if no pole lies in the right s-half plane, no multiple poles lie on the imaginary axis of the s-half plane and at least one single pole is present.
Controlled system in the state space
see also controller # state controller
In classical control theory, the analysis and calculation of control systems in the time domain was only of less importance than the methods in the frequency and s domain, such as the Laplace transformation, the frequency response and the root location method. Mainly linear time-invariant transfer elements with constant coefficients were dealt with. Nonlinear systems have been linearized.
Only with the advent of digital computers was it possible to calculate and simulate control loops using numerical methods. Instead of calculating the continuous behavior of the physical quantities of a dynamic system as f (t), it is converted into a quantized calculation method with constant small time intervals, the discretized time Δt. The dynamic system is described with difference equations and calculated algebraically.
The state space theory known since the 1960s comes from the USA by Rudolf E. Kalman . It cannot replace the above-mentioned classic control theory, but it can expand it to include some methods. The state space model is based on the system-theoretical concept of the state of a dynamic system. This model form allows many analysis and design methods in control engineering, such as B .:
- Nonlinear systems,
- Systems with multiple input and output variables,
- Linear transfer elements with time-dependent coefficients (time-variable systems),
- Synthesis of optimal control systems.
The model describes the relationship between the input signal u (t) and the output signal y (t) of a transmission system. This makes it possible to calculate the generated output signal y (t) for a given input signal u (t) using the model description.
When setting up the models, one starts from the basic physical laws, such as B. in electrical systems from Kirchhoff's laws, in mechanical systems from the conservation laws for energy and momentum.
In the models of the dynamics of a transmission system, the contents of the system memory describe the state of the system at a specific point in time. From the knowledge of the state of the memory at any point in time t = t (0), which is referred to as the initial state x (t0), and the course of the input variable e (t), the behavior of the model follows for all subsequent times.
These physical relationships are mathematically translated into a differential equation and then into a state space model. An alternative way to theoretical modeling is the experimental identification of a transmission system, in which the model is identified on the basis of a known input signal e (t) to the system via the behavior of the output signal.
The state of a linear dynamic system with n energy stores is described by n state variables or state variables , which are combined to form a state vector . The state variables describe the internal movement of the system. In transmission systems without differentiating components, they are physically the energy carriers of the system. In a spring-mass system these are z. B. the potential and kinetic energy components.
The state variables of a mathematical model of a controlled system with concentrated storage (as opposed to distributed storage) can be determined from a common system-describing differential equation. The terms of the derivatives of the output variable are integrated and fed back to the system input with the associated coefficients. In principle, this corresponds to the signal flow diagram of the classic solution of a differential equation using analog computing technology, with the state variables being the outputs of the integrators.
The state space representation is the description of a dynamic system through its state variables. All relationships between the state variables, the input variables and output variables are represented in the form of matrices and vectors.
Mathematically, the state differential equation is about the conversion of an n-th order differential equation into n first-order differential equations.
For control engineering, the integration of the state variables into a state controller instead of the classic output feedback is very advantageous for the dynamics of the control loop. The state variables act faster than the output feedback of a standard control loop. The treatment of control systems in the state space is primarily about the use of this dynamic property.
All state variables of a controlled system must be available for the state controller. They can be measured on the controlled system, but this is often not possible for various reasons. A remedy is provided by a state observer, which reconstructs the state variables for the state controller using a mathematical model of the controlled system.
Definition of terms for dynamic transmission systems in the state space
- State space :
- A dynamic system in the state space is described by its internal system variables, the state variables. The state variables are determined from the system-describing differential equation of a model of the controlled system through integration processes of all derivatives of the output variable.
- The state of a system with n energy stores is determined by n state variables . The state variables are the internal system variables that determine the dynamic transmission behavior. These are combined into a state vector . The value of the state variables at a specific point in time t is the state of the system. Physically, the state of a system is given by the behavior of its energy stores at a certain point in time through the initial conditions .
- The number of state variables of the state vector is the dimension of the state space.
- State space representation
- The state space representation is defined as the combination of the input quantities, output quantities and state variables of a transmission system in the form of matrices and vectors.
- The treatment of a system in the state space is not necessarily linked to the system description in the form of matrices. The time behavior of the output variable y (t) and the state variables x (t) can also easily be calculated and graphically represented by means of numerical methods as a function of any input signal w (t).
- State space model
- The state space model of a transmission system symbolically describes the normal control form using matrices and vectors. In a standardized form, it shows the relationship between the input signal u (t), the output signal y (t) and the additive feedback of the state variables to the input signal in the form of matrices and vectors. It describes single and multi-variable systems.
- The state space model block diagram is a simplified model showing the first derivative of the state vector and the simple integration of the state vector and its feedback. It symbolizes the n-th order differential equation converted into n-coupled state differential equations of the first order. The actual signal flows and state variables that result from the higher-order differential equation describing the system are displayed in the diagram of the signal flows of the normal control form.
- The standardized state differential equation and output equation belonging to the system completely describe the transmission system with matrices and vectors.
- The equations for the derivation of the state vector and the output variable y (t) result algebraically from the block diagram of the state space model.
- State variables
- The state variables (= state variables) physically describe the energy content of the storage elements contained in a dynamic system. They cannot change abruptly when the system is stimulated. B. Voltage on a capacitor, current in an inductance, in a spring-mass system the potential and kinetic energy components.
- Most linear transmission systems or higher-order controlled systems can be described by ordinary differential equations of the nth order. The state variables result from the differential equation by integrating all derivatives of the output variable y (t) and subtracting them with the associated coefficient from the input variable u (t) (= addition of negative coefficients of the poles of the transmission system).
- See the graphic of the status variables using an example of a 3rd order transfer element as step response in the article Control loop: step response of the status variables !
- System matrix
- The system matrix contains the coefficients of the state variables. Due to the normal control form, the system matrix can be created according to a relatively simple scheme. The coefficients of a transmission system of the nth order are in one row of the matrix.
- In multi-variable systems with coupled transmission elements, the determination of the state variables and the design of the system matrix can be time-consuming. A coupled transfer function or the associated differential equation can be determined for each output variable . The coefficients for the n * n system matrix are formed from this.
- Passage matrix
- In the normal case of control engineering, the pole-zero ratio n> m applies to the description of the transmission behavior of the controlled system, i.e. H. the number of poles n is greater than that of the zeros m of the system. In this case, the system cannot jump. The passage matrix or the passage factor becomes zero.
- Normal forms in the state space for linear transmission systems
- There are various forms of signal flow plans, of which the best known are the normal control form (also referred to as Frobenius form, control normal form or 1st standard form) and the observation normal form.
- In the matrix-vector representation of the equations of state, both normal forms have a fixed scheme of the coefficients in the system matrix of the differential equation describing the system or the transfer function.
- The normal control form shows the implementation and solution of the differential equation in the physical analog signal flows of the state variables including the output variable for a given input variable. It can be viewed as a further development of the method known in analog computing technology for solving an nth order differential equation with n integrators.
- It is particularly suitable for controller design, e.g. B. with the pole specification method. Of the n * n elements of the system matrix , only the last row depends on the transmission system.
-
- Observation normal form
- It is particularly suitable for checking the system properties for observability. Of the n * n elements of the system matrix , only the last column depends on the transmission system.
- Controllability and observability of transmission systems
- Controllability
- A system is controllable if it can be brought from any initial state to any final state after a finite time.
- In general, the following applies to the signal quantities:
- A system is completely state-controllable if, for each initial time, each initial state can be brought into any desired final state after a finite time by an unlimited control vector .
- If all states (state variables) of a system can be controlled, the system can also be controlled. See article Controllability
- Observability
- Condition observers can only be implemented if the system to be observed can be observed, which is the case with the vast majority of technical controlled systems.
- A linear transmission system can be observed if the initial state of the state vector can be determined after a finite time by measuring the output variable y (t) . The input variable u (t) must be known.
- A system is said to be fully observable if every initial state can be determined exactly from the measurements of the output signal y (t) in a certain time interval from .
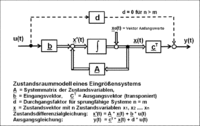
Block diagram of a state space model of a single variable system
The state space representation is based on a block diagram of the signal flows of a state space model. The illustration shown relates to a single-variable system, but can easily be extended to a multi-variable system.
The block diagram of the state space model symbolically shows the signal flows of a linear transmission system of the nth order, which was converted into n first order differential equations. It shows the connection between the derivation of the state vector and the system matrix of a linear transmission system with the input and output variables .
The mathematical description of the state space model is carried out by the state differential equation and by the output equation. Both together are called state space equations.
The block diagram of the state space model has a uniform form, but is represented differently as a single or multiple variable system. In the multi-variable system, the vectors and occur instead of the scalar input and output variables u (t) and y (t) . The signal flows of matrices and vectors are shown in the block diagram by double lines.
- Equations of the state space model according to the graphical signal flow diagram shown:
| equation | With single-size systems | With multi-size systems |
|---|---|---|
|
State differential equation (also state equation) |
||
| Output equation |
d = 0 for n> m |
= 0 for n> m |
- Meaning of the signals and system blocks of the state space model:
| meaning | Single size system | Multi-size system |
|---|---|---|
| Derivation of the state vector | ||
| State vector | ||
| State variable | ||
| Initial conditions vector | ||
| Input signals |
Input variable |
Input variable vector |
| Output signals |
Output variable |
Output variable vector |
| System matrix | ||
| Input matrix |
Input vector |
Input matrix |
| Output matrix |
Output vector (transposed) |
Output matrix |
| Passage matrix |
Passage factor = zero for n> m |
Passage matrix = zero for n> m |
Note: The quantities marked with vectors each mean a column or a row of a matrix.
State differential equation and output equation of the state space model in matrix-vector notation:
Single variable systems have only one input variable u (t) and one output variable y (t). The input matrices and output matrices merge into the input vector and output vector .
State differential equations of the single variable systems
Initial equation of the single variable systems:
The state space representation in the normal control form means a uniform form of the matrix representation with the following advantageous properties:
|
For further information that goes beyond the main article, state space representation , reference must be made to the specialist literature.
Multi-size systems
See also article: Controller # Controller for multi-variable systems !
If controlled systems have several input and output variables, they are called multi-variable systems. Several input signals of the path act alternately on the output variables and vice versa.
Examples of multi-variable systems can be found
- In the chemical industry, e.g. B. when mixing liquids of different temperatures to a target temperature and a certain amount of liquid
- in flight technology and a. For helicopters: The manipulated variables for the movement are the angle of attack of the main rotor and the tail rotor. B. the flight altitude and the yaw angle.
These systems can e.g. B. not be regulated satisfactorily by single-loop control systems.
Two-variable controlled systems
The structure of the two-variable controlled systems of the most popular multi-variable controlled systems is shown below.
- The controlled system has two input variables and two output variables.
- Both output variables are dynamically linked to the other input variable.
- Depending on the sign of the addition points, a distinction is made between positive and negative coupling. In two-variable control systems, negative coupling means that only one of the two coupling points intervenes negatively.
- The coupling can take place at the exit of the main line as well as at the entrance.
Like single-loop control systems, multivariable control systems can be described both in the time domain by differential equations, as a state representation and in the frequency domain by transfer functions.
According to the block diagram with the coupling points at the outputs, also apply to linear controlled systems based on the superimposition principle
- G11 (s) and G22 (s) as main lines and
- G12 (s) and G21 (s) as coupling links.
The associated transfer functions of the two output variables for the coupling at the output are:
Analogous to the two-variable controlled systems with coupling at the output, there are two-variable controlled systems with the coupling at the input. The associated transfer functions of the two output variables with the coupling at the input are:
The graphic shows the step response for a two-variable controlled system with coupling at the output. With positive coupling and transmission systems with compensation without amplification factors, the output variable in the steady state is always y (t) = 2 * u (t). In the case of a negative coupling, the output variable is y (t) = 0 in the steady state under the same conditions.Y (t) can temporarily assume positive or negative values depending on the behavior of the coupling path.
Multi-variable control loops
Controlled systems with several input and output variables are also controlled by controllers with several input and output variables. If there are several control variables, several setpoints and manipulated variables are also required to create a multi-loop control loop.
The usual design strategy for controllers in single-loop control loops - e.g. B. Pole zero point compensation - does not produce satisfactory results with multivariable control systems.
The method of eliminating the coupling through a special structure of the controller provides a remedy. For the two-variable control loops, four controllers are required, which can convert a two-variable control loop into two single-loop control loops.
Other methods for the simplification of multi-variable systems are “model reductions” and “approximate decoupling”. See also controllers for multi-variable systems .
See also
literature
- Gerd Schulz: Control engineering 1 . 3. Edition. Oldenbourg Publishing House, 2004.
- Gerd Schulz: Control engineering: multi-variable control . Volume 2. Oldenbourg publishing house, 2002.
- Serge Zacher, Manfred Reuter: Control technology for engineers . 14th edition. Springer Vieweg Verlag, 2014, ISBN 978-3-8348-1786-0
- Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Verlag Europa-Lehrmittel, 2019, ISBN 978-3-8085-5869-0 .
- Heinz Unbehauen : Control Engineering Volume 1. Vieweg, Braunschweig 2005, ISBN 3-528-93332-1 .
Individual evidence
- ↑ Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . Chapter: Harmonic linearization with the description function.
- ↑ Gunter Schwarze : Algorithmic determination of the transfer function of linear models with constant concentrated parameters for analog systems with one input and one output by analyzing the output signals belonging to characteristic test signals in the time domain. TH Magdeburg, Faculty of Basic Sciences, habilitation thesis, Magdeburg 1967.
- ↑ Oliver Nelles: Chapter: "Description of dynamic systems in the state space" . In: Lecture concept for measurement and control technology II. University of Siegen, May 4, 2010, 364 pages.