Control loop

The closed cycle for influencing a physical variable in a technical or other system is called a control loop . The course of action or the process taking place is called control , and its treatment in technical systems is called control technology. What is essential here is the feedback of the current value of the physical variable to the ( controller ), which counteracts any deviation from its setpoint ( negative feedback ). To describe the individual action steps, the control loop is broken down into corresponding sections (see adjacent block diagram).
It is the controller's task to regulate the disturbance variables and to determine the time behavior of the controlled variable with regard to the static and dynamic behavior according to specified requirements . The disadvantage of a regulation resulting from the feedback structure is the possible problem of instability.
The mathematical model of the controlled system is required to design a controller . For multi-variable systems (MIMO), the controller design with the state space representation is suitable ; for non-linear and dead-time systems (SISO), numerical calculation is recommended. The classic graphic controller design methods ( Bode diagram , locus of the frequency response , root location method) are only of didactic and informative significance.
Thanks to modern electronics, controller structures of any complexity can be implemented with reasonable economic effort. In many cases, digital controllers are used instead of analog controllers and possibly combined with digital measuring and actuating elements. The digital signals are value and time discrete signals. These control loops behave like analog control loops if the resolution and sampling rate is high enough.
introduction
A real control loop consists of several individual components of the controlled system and the controller, each of which has a specific time behavior. While the controlled system is usually present as a technical system, a system analysis of the controlled system is required for the mathematical treatment of the closed control loop, from which a mathematical model can be determined. The model should largely correspond to the time behavior of the real controlled system. The observation of a signal course on a transmission system for a given input signal starts at and ends for the course of the output signal with .
In connection with the controlled system model, a controller can be parameterized that ensures the stability of the closed control loop after the closing condition .
In general, the parameters of the controller cannot be optimally set manually in the case of more complex controlled systems. Industrial control processes with maladjustments of the controller can lead to the destruction of the systems due to the increasing amplitudes of the controlled variable.
The most common mathematical system descriptions are the differential equation , the transfer function , the frequency response and the discrete-time difference equation .
The aim of the mathematical description of control loop elements is to calculate the dynamic input-output behavior of individual components, closed control loops and their stability.
Because of the required quality criteria ( quality of control ) of the transient of the controlled variable heuristic method "trial and error" in which offline - simulation of the control loop is usually the case.
Simulation of the input-output behavior of a control loop
Unfortunately, individual components of most technical control systems behave non-linearly. The transfer function and its algebraic calculation may only be used for linear transfer systems.
If, for example, the controlled systems contain a dead time (transport time, gear backlash), limiting effects of some components or other non-linearities, practically only the discrete-time calculation of the control loop with difference equations in connection with logical functions as a numerical system description is possible for the system calculation. All components of the open control loop are described by difference equations and logical functions. The open control loop is closed by the relationship as the input variable of the controller, which determines the desired behavior of the control loop with its time behavior.
Difference equations or a chain of difference equations that describe several elementary systems connected in series allow the output variable to be calculated algebraically for a small time step depending on the input signal . The numerical overall solution of the system takes place - with simple difference equations - recursively over many calculation sequences in small constant time intervals. The form of the overall solution is thus in tabular form.
The typical form of a recursive difference equation for common control loop elements (linear factors) is:
- .
It is . The sequence describes a finite number of subsequent members .
Difference equations of the linear time-dependent system components can be derived from ordinary differential equations in which the differential quotients are replaced by difference quotients . Nonlinear transmission systems can e.g. B. can be described by logical statements such as IF-THEN-ELSE statements or tables.
See article difference equation .
Digital controllers
Digital control means that the input signal of a dynamic system or a subsystem is sampled at certain discrete points in time, calculated synchronously and output as a digital output signal. Other terms refer to this process as "time-discrete control" or also as "sampling control".
Digital controllers are implemented by microcomputers . They process suitable difference equations for the desired control behavior of the overall system.
Since the controlled systems are usually analog systems, the interface of the system requires an analog input signal via a DA converter .
Advantages: One-time hardware development effort, simple parametric system changes via software, implementation of more complex controller structures, multitasking .
Disadvantages: The use of a digital controller is only worthwhile for larger production quantities due to the increased technical effort.
See article Digital Controller , Z-Transform and Difference Equation .
Basics of the control loop model
Dynamic systems with concentrated parameters as single-variable and multi-variable systems can behave linearly, nonlinearly, time-invariant, time-variant and globally proportional, integral and differential. Systems with concentrated parameters (spring-mass system), in contrast to systems with distributed parameters (heat flow in a homogeneous medium), have no spatial expansion.
The task of a mathematical model of a real dynamic process or a technical process that has yet to be configured serves to identify and predict the system behavior.
The mathematical model of a control loop describes all external influencing variables such as disturbance variables and input signals on the closed operating sequence of the control loop. The behavior of the output variables such as the controlled variables as well as interesting intermediate variables (manipulated variables) as a function of the input signals and the parameters of the controller and controlled system are of particular interest.
Depending on the specifications of the control engineering task, the mathematical model of the controlled system is required to determine a suitable controller.
With simple linear physical systems, mathematical models can precisely describe a controlled system using a common differential equation ( = theoretical modeling ).
In most applications, transmission systems (controlled systems) also have non-linear components and are subject to dead time. For such systems, the system response is recorded experimentally using suitable test signals and a mathematical model is sought that reproduces the measured course of the output variable y (t) ( = experimental process analysis ). A model defined in this way can easily be calculated using numerical methods. If non-linear subsystems are included in the overall system, they must be recorded separately and defined using tables of values.
Globally proportional control systems of a higher order with dead time can be described relatively precisely by PT2-Tt elements. Globally integral control systems can also be described by PT2-Tt-I elements.
To understand the model of a dynamic system, the most important terms of internal system memory must be understood.
Details see article Systems Theory (Engineering Sciences) !
The single loop control loop

The analysis of functions requires that the control loop parts be viewed individually. Thus, the term describes open loop ( open loop ), the behavior of the controller and controlled system without feedback. The process of closing (i.e. switching on the return) is considered separately in some cases.
Transfer functions of the control loop
The transmission behavior of linear control loop systems ( linear time-invariant system , LZI system) is generally described by differential equations (see also linear ordinary differential equation ). The calculation of the systems is greatly simplified if the solution of the differential equation is not carried out in the time domain but in the image domain (s domain) using Laplace transformation . The system calculation then refers to simple algebraic operations. The prerequisite is that the system is an LZI system and the initial conditions are zero.
The transfer function of a transmission system is the ratio of the Laplace-transformed output quantity Y ( s ) to the Laplace-transformed input quantity U ( s ) with s as the Laplace variable.
The transfer function of a dynamic linear time-invariant system:
- and the control loop
is the most frequently presented description of the input-output behavior of control loop elements in control engineering.
The poles and zeros of the transfer function are the most important parameters of the system behavior.
Example of a transfer function of the polynomial representation and the decomposition into the pole-zero representation with real linear factors:
By determining the zeros , the polynomials of the transfer function can be brought into a product form ( linear factors ) in the numerator and denominator. The product representation in the numerator and denominator of the transfer function is mathematically identical to the polynomial representation.
The poles (zeros of the denominator) or zeros (zeros of the numerator) are either zero, real or conjugate complex .
By breaking down the numerator and denominator polynomials into poles and zeros, the factorial representation of the transfer function results, i.e. H. into the 3 possible basic systems in the complex frequency range (s-range, s-level):
each in combinations in the numerator and denominator of the transfer function.
(See controlled system # Characterization of the controlled systems )
The poles ( zeros of the denominator polynomial) of the transfer function are at the same time the solutions of the system, which will be shown in detail later.
If the transfer function of a controlled system or an approximate model of the controlled system is available, a suitable controller can be determined relatively easily. It should be noted, however, that a certain loop gain can result in a high manipulated variable u (t) that the controlled system cannot process. The manipulated variable is limited and the transfer function of the open or closed control loop is no longer valid.
The signal limitation is an effect of several non-linear systems occurring in realistic controlled systems. This also applies to dead time systems and systems with non-linear characteristics. They cannot be treated with the transfer function. There is probably a transcendent transfer function for dead-time systems :
- ,
which can be attached multiplicatively to a transfer function G (s), but is not suitable for the algebraic calculation with the transfer function.
Various classic methods of stability analysis are also invalid for the effects mentioned.
Requirements for a control loop
- The control loop must be stable.
- The stability of the control loop with linear time-invariant transmission systems depends on the order and parameters of the system, on the structure of the controller and on the parameters of the controller.
- If a control system is made up of linear time-invariant systems in connection with a controller to form a control loop, two advantages are gained in relation to the behavior of the control system:
- the controlled variable adjusts to the level of the setpoint , disturbance variables are minimized,
- the dominant time constant of the controlled variable is reduced approximately by the factor of the loop gain.
- If there are differentiating PD elements in the controller, the gain is additionally increased by a dynamic component. The manipulated variable can assume very large values. This results from the calculation of the closing condition ( signal flow algebra ) of the control loop.
- A control system that has been converted into a controlled system cannot be made faster without a supply of energy. This example shows the effect of the device-related signal limitation of the manipulated variable , which often functions as an interface between control signals and control energy (e.g. actuators, valves, etc.). It is a matter of judgment whether the power interface belongs to the controller or to the controlled system.
- The transfer function of this example of a simple control loop does not contain any indication of a signal limitation and is therefore incorrect if there is a signal limitation. Transfer functions only apply to linear time-invariant systems.
- You can ignore signal limitations and you will have a stable control loop. However, the transition behavior of the controlled variable in the case of signal limitations does not correspond to the transfer function of the control loop.
- An important method of determining the stability is the analysis of the denominator polynomial of the transfer function of the control loop, whether the poles (zeros of the denominator that make the equation zero) lie in the left half-plane of the s. See chapter "Stability of the control loop"!
- The control loop should exhibit good management behavior and disruptive behavior.
- If no special control measures are taken, these are contradicting requirements.
- The control loop should behave robustly.
- “Robust” is understood to mean the influence of the gradual changes in the parameters of the controller and the controlled system on the dynamics of the control loop. This by internal and external environmental influences such. Changes in parameters, such as aging, friction, and corrosion, must be within an approved tolerance range. The robustness behavior is also referred to as the influence of the “internal disturbance variables” of a control loop.
These requirements can only be met by compromising the controller parameters. With high requirements z. More complex controller structures are required, for example in terms of the management behavior and / or disturbance behavior.
Management behavior of a control loop
The control loop should have good leadership behavior, i. H. After specifying a reference variable W ( s ) or a change in the reference variable (setpoint change), a certain dynamic behavior is desired with which the controlled variable approaches the setpoint of the reference variable. In addition to the dynamic behavior, the stationary accuracy is of interest. A typical input test signal is the unit jump. (See table test signals )
The term setpoint is understood to mean a certain value of the reference variable. If the reference variable is a time-dependent variable, the control loop or the controlled variable must show good follow-up behavior. A typical input test signal is the slope function. (See table test signals .)
By default, the control loop G ( s ) (see signal flow algebra ) is composed of the transfer functions of the controller G R ( s ) and the system G S ( s ). If the metrological acquisition of the controlled variable has a time behavior that must be taken into account, then the branch of feedback of the controlled variable receives the metrological device with the transfer function G M ( s ).
- According to the closing condition with negative coupling (negative coupling), the lead transfer function of the control loop is:
- If the time behavior of G M ( s ) is negligible, then the transfer function reads:
- or in the summary of G R ( s ) G S ( s ) = G O ( s ) as an open control loop:
Disturbance behavior of a control loop
The control loop should show good disturbance behavior. The influence of the disturbance variable should be small. The point of attack of the disturbance variables is often the controlled variable. The attack site can also be within the controlled system or at the entrance to the controlled system. To describe the disturbance behavior f ( t ), the point of attack and the disturbance signal course of the disturbance variable must be known. The worst case of the interference signal d (t) is when it suddenly has an additive effect on the steady state of the controlled variable y (t). The polarity of the disturbance can be positive or negative. Depending on the dynamics of the control loop, the disturbance deviation is corrected more or less quickly. If the open control loop has an I element, a constant disturbance variable is fully regulated in the steady state.
- The disturbance variable D (s) acts on the output of the controlled system Y (s)
- Input variable = disturbance variable D ( s )
Output variable = controlled variable Y ( s ). - Disturbance transfer function G D ( s ) for the disturbance acting on the output of the controlled system Y ( s ):
- The disturbance variable D (s) acts on the input U (s) of the controlled system
- Input variable = disturbance variable D ( s )
Output variable = controlled variable Y ( s ). - Disturbance transfer function for the disturbance acting on the input of the controlled system:
- The decisive difference between a disturbance transfer function with the disturbance variable attacking the input instead of the output is the fact that the disturbance signal has to pass through the controlled system with its delay components when it is attacked and is dampened accordingly. When the interfering signal attacks the output of the controlled system, the interfering signal initially has an undamped effect on the controlled variable until the interfering influence is reduced in accordance with the dynamics of the control loop.
- Control loops in which the disturbance variable acts at the input or within the controlled system require a different optimal (higher) loop gain for the disturbance behavior than for the command behavior. A higher loop gain - than necessary for the optimal control behavior - leads to an increase in the tendency of the controlled variable y (t) to oscillate for fast control input variables.
- If the control behavior is not so important when the control variable changes, the overshoot of the controlled variable y (t) can be limited by limiting the increase in the setpoint of the control variable.
- If optimal control and disturbance behavior is required, special controller structures must be used.
- Restriction of the superposition principle when a disturbance variable acts within the control loop.
- If a disturbance variable z. B. at the input of the controlled system, the superposition principle only applies within the controller or within the controlled system.
-
Impact:
- If one shifts a component of the controller beyond the point of intervention of the disturbance variable, then the disturbance transfer function changes. This changes the interference suppression.
- If a component of the controller with a component of the path that lies behind the intervention point of the disturbance variable is shortened against each other in a pole-zero point compensation (e.g. PD element against PT1 element), the behavior of the controlled variable is completely different compared to the unabridged state.
- In practice on a hardware controlled system, this behavior is irrelevant because you can hardly move a component of the controller into the controlled system without tricks. For the simulation of a control loop with a disturbance variable within the controlled system, the limitation of the superposition principle shown must be observed.
Terms to describe the dynamics
- Overall control loop gain (also loop gain, P gain)
- The loop gain K of the open control loop is understood to be the product of all factors of the individual transmission systems. For controllers with an I-element in the parallel representation, e.g. B. With the PID controller, the total gain of the control loop is K = K PID · 1 / Tn.
- As far as possible, delay elements in the controlled system are compensated for by PD elements in the controller.
- In order to be able to close the open control loop, the overall gain of the open control loop must first be determined, which has a decisive influence on the course of the controlled variable when the setpoint changes or when a disturbance variable is attacked. There are a number of stability procedures for determining the overall gain of the open control loop, which are associated with more or fewer restrictions depending on the behavior of the controlled system:
- Settling (also transition behavior, transient behavior)
- The settling ( overshooting ) of an output signal of a transmission system as a result of a change in the input signal is a dynamic process f ( t ) in which the output variable of the system moves to a steady state in the case of stable system behavior.
- Settling time is understood here as the time interval between the start of the input signal change and the completed dynamic change in the output signal, the start of the steady state of the output signal. Usually the decay of the signal change is defined as complete with a tolerance value of less than approx. 10% to 5%.
- The overshoot time is the period of the dynamic process from reaching the setpoint until it subsides. The values of the reaching and the decay of the oscillation are often assigned to a tolerance range of ± 10% to ± 5%.
- Setpoint sequence
- The controlled variable follows the setpoint (fixed value control). After the settling time, the controlled variable adjusts to the level of the setpoint.
- If there is an I component in the control loop, the system deviation e (t) becomes zero after the settling time with a constant disturbance variable.
- Follow-up behavior
- Follow-up control describes the control behavior when the reference variable w (t) is controlled as a time sequence. Good follow-up behavior is understood to mean a small difference between the controlled variable and the reference variable after the transient process.
- If w ( t ) is a continuous time behavior (constant speed), a follow-up error results in a control loop with or without an I component.
- For a control loop with 2 I elements with a constant rate of increase of the reference variable w ( t ), the controlled variable y ( t ) follows after the reference variable has settled without a control difference.
- Trajectory sequence:
- ( Trajectory in mathematics : trajectory, e.g. signal curve f ( t ) as a solution to a differential equation)
- The trajectory sequence is a term used in follow-up control in which the reference variable w ( t ) is controlled as a function of time. The trajectory sequence is therefore a time-controlled or time-dependent reference variable w ( t ).
- The term trajectory sequence is often used in the state space representation.
- Trajectory sequence with adaptation to the dynamic system:
- Inner model principle: A control loop can completely suppress the consequential error of a reference variable if it contains an "inner model" of the reference signal. This means that the open control loop with the controller and the controlled system must contain the reference variable model for which the setpoint sequence is to be achieved.
- Interference signal of any form with adaptation to the dynamic system
- Inner model principle: The model of the disturbance is integrated into the controller.
- A control loop can completely suppress an interfering signal if it contains an "inner model" of the interfering signal.
- Large signal behavior
- Under large signal behavior is here understood that a regulator is designed for a control loop for a maximum reference variable. A standard input jump = 1 in this case means a 100% signal. Does a PT2 system allow the use of a P controller (depending on the time constants) with e.g. B. a P gain of K = 50, then the output variable of the controller is initially 50 and after the settling time is static at 0.98. If the controlled system does not allow an input variable u ( t ) of 50 = 5000%, but limits this value, then the step response of the controlled variable y ( t ) is displayed in a distorted and delayed manner in the settling process. The effect of the increase in the manipulated variable is increased if the controller contains a PD element.
- With controllers with PI and PID behavior, this effect is not so pronounced because the I behavior means that a large loop gain is not possible due to the additional phase rotation of the system. With the PI controller, the signal increase in the PD element is fully compensated for by the I element. In the PID controller, a PD element contributes to the signal increase.
- Conclusion: The transfer function of a transfer system or a control loop only determines the dynamic behavior of the output variable if there are no signal limitations within the system chain. The transfer function is invalid in the case of signal limitations!
- See article Large signal behavior .
- Quality criteria ( control quality , integral criteria , quality of the control behavior)
- This is understood to be a measure of the time deviation of the step response of the control difference y ( t ) to the step function of the reference variable w ( t ) over the full transient process through integration.
- With these integral criteria, the system deviation w ( t ) - y ( t ) is integrated in various ways for the duration of the transient process. A distinction is made between:
- Linear ruled surface
- Square ruled surface
- Amount control area: (integration of the amount of the control difference)
- ITAE criterion : By multiplying it by time, the small vibration amplitudes are taken into account more strongly.
- These quality criteria, known since the beginning of the 20th century, relate to the step response of a control loop and include the following assessment criteria:
- Rise time (even ., Engl rise time): The rise time is determined by the projection of the inflectional tangent to the time axis. It corresponds to the period between the points of intersection on the time axis and the level of the stationary value.
- Delay time (. Engl delay time, and dead time): time from the input leap the intersection of inflectional tangent on the timeline.
- Settling time = T s ( . Engl settling time): time from t = 0 until a tolerance band for. B. 5% or 2% of the stationary step response,
- Overshoot range ü = standardized largest overshoot range based on the step response of the stationary controlled variable,
- Stationary control errors are not taken into account for the quality assessment.
- If these variables could be minimized together, the control loop would be optimally dimensioned. Unfortunately, when the controller parameters are changed, the values mentioned show partially the opposite behavior. For example, if the loop gain is increased, the rise time is shortened; the settling time and the overshoot increase.
- The control loop is optimized with regard to the command, disturbance and robustness behavior. The type of quality criteria mentioned above must be specified in a project specification sheet.
- Model of the controlled system and the control loop
- The model ( modeling ) of a controlled system or a transmission system is understood to be the abstract image of a mostly technical (possibly physical, chemical, biological) facility. The model is obtained analytically using basic equations or experimentally as a mathematical model.
- The modeling of a controlled system in the time domain is done experimentally in the simplest form by graphically recording the step response with subsequent analysis, if mathematically possible by setting up differential equations or by setting up a state space model.
- (See controlled system # Experimental system identification of controlled systems according to the step response )
- The modeling in the frequency domain is the representation of the controlled system model as a transfer function.
- Nonlinear systems can neither be described by ordinary differential equations nor by transfer functions. A restricted representation is only possible in the state space ( controlled system # controlled system in the state space , state space representation ) or by numerical time-discretized methods.
Stability of the control loop
The various classic graphic methods of determining stability mostly relate to determining whether the closed control loop is stable on the open control loop - consisting of the controlled system and the controller. Even the presence of a dead time , which often occurs in the controlled systems, causes some of these methods to fail.
One method of determining the stability in the frequency range (s range) relates to the position of the poles and zeros of the control loop in the s plane. If the transfer factor, the poles and zeros of the control loop are known, the behavior of the control loop is fully described. However, this method is only suitable for linear time-invariant systems without dead time.
If the manipulated variable is limited, it can only be determined whether the control loop is stable. It is assumed that the manipulated variable limit allows at least a 2 to 3-fold value of the maximum reference variable.
Another method for selecting and parameterizing a controller is to simulate a control loop - i.e. a model made up of a controller and a controlled system - through numerical treatment of time-discrete transmission systems.
In connection with logical operators ( logical operator ) and tables, mixed LZI and non-linear time-independent systems can also be calculated.
There are different definitions and terms of stability:
Internal stability
If the transfer function of a transmission system or a control loop is present:
The poles of a transfer function determine the stability and the speed of the system movement. The zeros of a transfer function only affect the amplitudes of the system.
| A transmission system is internally stable if all (partial) transmission functions only have poles in the left half-plane. |
|---|
External stability (BIBO stability)
If the hardware of a transmission system or a control loop or an exact model is present with the input and output signal:
|
A transmission system is said to be externally stable if any limited input signal to the system also produces a limited output signal. (See BIBO stability ) |
Stability as a function of the parameters of the control device
There are a number of mathematical and graphic methods for this.
|
Meaning of the poles and zeros of the transfer function of a transmission system
The transmission behavior of a transmission system in the frequency domain as well as in the time domain is determined by the coefficients and the degree of the transfer function. The product representation of a transfer function in basic systems G ( s ) that can no longer be split up requires the determination of the poles and zeros of the numerator polynomial ( polynomial ) and the denominator polynomial of the transfer function.
The poles of the denominator polynomial are also the solution of the system. The poles determine, among other things, the stability of the system. Because of the importance of the terms poles and zeros, their behavior is shown in the following chapters.
The general representation of a transfer function as a rationally broken function of a transfer system with the output signal Y (s) and the input signal U (s) is:
The behavior of the system from the input and output signals is described by means of the transfer function.
The transmission behavior of a transmission system is determined by:
- the structure of the transfer function, d. H. Degree of numerator and denominator polynomial,
- the coefficients of the polynomials
The polynomial representation - in contrast to the product representation - of the transfer function of a transmission system results:
- by the Laplace transform of an ordinary differential equation describing the transmission system, or
- if the transfer function of an open control loop Go ( s ) in the product representation is subjected to the closing condition with
The denominator of the transfer function
is referred to as a “characteristic equation” or also as a “characteristic polynomial”. The characteristic polynomial is identical to the denominator polynomial of the control loop.
Knowing the zeros of a polynomial is very important for converting the polynomial into the product representation and for assessing the stability of a transmission system as follows:
- Definition of zeros and poles
- When representing the transfer function as a rationally broken function, the zeros of the numerator polynomial that make the transfer function zero are referred to as zeros . The zeros of the denominator polynomial are called poles . After the transition from the open to the closed circle, the poles are also referred to as roots .
- The determination of the zeros and poles of the polynomials of a transfer function allows the product to be represented.
- Knowing the poles of the characteristic equation results in the solution of the transmission system in the time domain. The transfer function in the product representation leads directly to a solution in the time domain for a given input signal via the Laplace transform.
- Calculation example:
- The normal form of the product representation is transformed in such a way that the factor before the Laplace variable s disappears: (conversion of time constant representation into pole-zero representation)
- Pole:
- The output variable of a dynamic system y (t) of the time domain for a transmission system in the s domain is:
- Laplace inverse transformation with the help of Laplace transformation tables:
- (= Impulse response because of )
- The poles of a transfer function - in contrast to the zeros - appear in the time domain only in the exponents of the exponential functions.
- The zeros of a transfer function do not affect the stability of the system or the speed of the system movement. However, they have a considerable influence on the amplitude of the system response.
- For reasons of stability, the transfer function for the closed control loop must always have one more pole than there are zeros.
- To determine the poles and zeros of transfer functions, one can use ready-made computer programs for transfer functions up to 4th order. Such programs can also be found on the Internet under the search term "zeros of polynomials".
Significance of the poles and zeros for the stability of the control loop
- Only negative poles of a transmission system mean that the system is stable. 1 pole in the origin ( ) means limit stability. 2 poles in the origin ( ) means instability.
- If a negative pole of a transfer function is close to the origin (imaginary axis) and far from the zeros, its influence is great. A small value of the amount of the pole means a large time constant.
- If a negative pole of a transfer function is close to or directly on a negative zero, they largely cancel each other out in their effect. (Pole zero compensation).
- Pole pairs are the complex conjugate poles of an oscillation system of the 2nd order ( PT2 element ), which contain a real and an imaginary component. They naturally arise in storing technical systems through the exchange of energy (e.g. spring-mass system) in a controlled system or through real poles within an open control loop that is closed with a certain critical loop gain K. Further additional poles that lie to the left of the poles and at a distance in the left s-half plane have little influence.
- Pole pairs with a negative real part and an imaginary part cause a dampened oscillating signal curve in the time domain
- Pole pairs with a vanishing small imaginary part compared to the negative real part cause an aperiodic signal curve in the time domain
- Pole pairs with vanishing small real parts compared to the imaginary part cause a purely sinusoidal waveform in the time domain
- Poles or pole pairs with a positive real part cause instability in the time domain due to a monotonically increasing signal curve or increasingly oscillating signal amplitude
- Unstable poles in the right half-plane in the open control loop must not be compensated for by positive zeros, otherwise instability occurs.
- Pole zero compensation
- Is the mathematical model of the controlled system known, i. H. the transfer function of the controlled system is known, all delay elements can
- the route through PD links
- of the (ideal) controller can be compensated if the time constants are identical.
- The correctness of this representation results from the observation in the frequency domain by applying the Bode diagram or in the time domain by applying the inverse Laplace transform with a defined input test signal.
- The pole-zero compensation in transmission systems with signal limitations distort and delay the transition behavior of the controlled variable y ( t ).
Influence of non-linear transmission systems on the control loop
Nonlinear transmission systems such as signal limitations and systems with nonlinear characteristics cannot be described by linear ordinary differential equations ( ordinary differential equation ). Therefore, they cannot be treated like LZI systems. Depending on the size or influence of these systems, the controlled variable y (t) can deviate considerably from a desired behavior if these influences are not taken into account. If you want to consider the closed course of the controlled variable y (t) as a function of the reference variable or disturbance variable over the entire settling time for a single-loop control loop with non-linear systems, then the application of numerical time-discrete methods with the help of commercially available computer programs or with your own programs is suitable by using difference equations in conjunction with logical commands. This also applies to the calculation of combinations of LZI systems with logical operators for the treatment of non-linear systems.
- Dead time systems
- can only be treated with the transfer function in the frequency domain.
- The so-called transcendent transfer function
- is only suitable for z. B. graphical stability methods such as the Bode diagram or the locus of the frequency response.
- Signal limitation of the manipulated variable
- It is the most common non-linear form of transmission systems and is usually positioned in the interface of the actuator between the controller output and the input of the controlled system. As already shown for the PID controller , the classic controllers of the analog design with operational amplifiers behave completely differently from digital controllers using the discrete-time method.
- Typical limitation of the analog controller:
- Operational amplifiers operated with a supply voltage of ± 15 V, for example, are often operated in the active working range of ± 10 V. A 100% signal of 10 V is already limited at 13 V.
- Another disadvantage: A PD or PID controller requires a so-called parasitic RC time constant because only a limited amount of energy is available at the operational amplifier output with the standard RC circuit when differentiating.
- A typical parasitic time constant is Tpar = 0.1 * Tv.
- Numerical digital controllers have no problem with large amplitudes because only numerical values are calculated. For the implementation of the technical equipment of the manipulated variable, as for all controllers, if signal limitations occur, the transfer function of the control loop is invalid.
- Wind-up effect
- The wind-up effect relates to controllers with PI or PID behavior. The manipulated variable u, which can also be in the input of the controlled system , is limited (see non-linear transmission systems ), but the associated I component of the controller can assume even higher values. If the manipulated variable falls below the limit during the control process, the I component has assumed a value that is too high. B. is delayed when the controlled variable overshoots. The controlled variable reaches the value of the setpoint with a delay.
- This effect occurs with all controllers with I behavior.
- This can be remedied by the wind-up correction by blocking the I element when the manipulated variable is limited. This means that the output of the I element can only change if the manipulated variable is effective again within a linear working range.
- This wind-up correction only applies to controllers in a parallel structure. In the product presentation of a z. B. PID controller, the PD elements do not work when the I element is locked.
- The better design strategy of the PID controller with manipulated variable limitation in the product representation is:
- Sequence of the controller systems: I-element - PD-element 1 - PD-element 2 - manipulated variable limitation: so that smaller numerical values arise
- In the case of limitations, the pole zero point compensation is only a reference point, increase the lead time Tv compared to the dominant time constant T.
- Halve the loop gain if necessary
- However, it is easier to dimension the control loop using a controller in a product representation and to convert and implement the parameters of the controller in a parallel representation.
- Ideal PID controller in product representation:
- Ideal PID controller in parallel representation:
- Conversion of the ideal PID controller from the product representation to the parallel representation:
- .
- Time-independent systems with non-linear characteristics
- As a rule, linearity is assumed in a certain area around the operating point of a non-linear system. Must be a non-linear system to be considered in a wide range of characteristics, systems with non-linear characteristic as shown in articles can control path described, be treated by special mathematical consuming procedures.
- In the case of combinations of mixed linear and non-linear systems, for reasons of simplicity, only the simulation of the control loop using numerical, time-discretized methods is recommended. The controller determined in this way is designed as a programmable digital controller.
Brief description of known graphic stability methods
Stability condition with the locus of the frequency response
The frequency response equation ( frequency response ) of the open circle is resolved according to the real part and the imaginary part and entered in a coordinate system. The vertical axis shows the data of the imaginary parts, the horizontal axis the real parts. According to Nyquist, the stability condition is:
If the critical point (-1; j0) on the left (negative) side of the axis of the real parts is not wrapped around or touched when passing through the locus of the open control loop Fo (jω) in the direction of increasing values of ω, the closed control loop is stable. For practical reasons, the critical point (-1; j0) should be moved to (-0.5; j0) in order to achieve a certain stability reserve.
Stability condition in the Bode diagram with the simplified stability criterion from Nyquist
In contrast to the locus curve of the frequency response, the Bode diagram plots the magnitude and phase angle in two separate diagrams, as amplitude response and phase response. The Bode diagram has a logarithmic scale. In the case of the amplitude response, the amount F (jω) is plotted on the ordinate and the angular frequency ω on the abscissa. In the phase response , the phase angle (linear) is plotted on the ordinate, the angular frequency ω on the abscissa (logarithmic).
The advantages of this method are the direct drawing of the asymptotes as straight lines of the amplitude response, the convenient multiplication by logarithmic addition, the direct reading of the time constants and the quick recognition of the stability of the closed control loop. In regular systems, the phase response can be calculated from the amplitude response and does not necessarily have to be drawn.
The stability criterion is derived from the Nyquist stability criterion :
A closed control loop is stable if the lagging phase shift φ from the output to the input signal of the open loop with the loop gain K = 1 and φ> −180 °. The attenuation of the closed circuit becomes more favorable, the greater the phase distance to the −180 ° line. This distance, which lies above the - 180 ° line, is called the phase edge or phase reserve and should be around 50 ° ± 10 °.
Stability with the root locus
Explanation of terms : When considering the open to the closed control loop, the zeros of the denominator of the rationally broken function are designated with roots instead of poles.
The root locus curve (see also the root locus curve method ) is a graphic representation of the position of the poles and zeros of the complex guide transfer function Fo (s) of an open control loop. Depending on a parameter, usually on the loop gain of the open control loop, the position of the poles of the closed control loop can be inferred from the root locus. The dynamic behavior of the closed control loop depends on the pole distribution, which in turn is determined by the choice of the controller parameters.
The graphic representation takes place in the s-plane , the real part is plotted on the abscissa, the imaginary part on the ordinate. There are several rules for the relatively complex construction of the root locus. If all poles and zeros are in the left half-plane (-) , the closed control loop is stable. If one or more poles are in the right half-plane (+) , the system is unstable. The root location method cannot be applied to systems with dead times.
Hurwitz criterion
This stability test was developed by Routh and Hurwitz, but has become known through Hurwitz ( Hurwitz criterion ). The Hurwitz criterion provides information about the stability of the closed circle even without explicit calculation of the poles; knowledge of the homogeneous differential equation or the characteristic differential equation is sufficient. The characteristic differential equation is identical to the denominator polynomial set equal to zero of the command transfer function G (s) or the disturbance transfer function Gz (s):
Conditions for the stability criterion:
- The transfer function of the closed circuit G (s) must be known.
- For the stability of the system it is necessary that all coefficients a are present and have the same sign .
- The "Hurwitz" determinants Di must all be> 0.
- A control loop with a dead time element cannot be handled.
Evaluation of known stability methods for the controller design
For a realistic controlled system consisting of linear time-invariant systems in connection with systems that cannot be described with linear ordinary differential equations ( ordinary differential equation ), the following restrictions apply to the parameterization of the controller for the specified stability methods.
Designation of the transmission systems:
- LZI = linear time-invariant systems ( linear time-invariant system )
- LZV = linear time-variant systems
- Tt = dead time element ( dead time (control technology) )
- Limiting a signal
- Non-linear characteristic ( non-linear system )
- MIMO = multi-variable systems, ( MIMO : Multiple Input Multiple Output)
| Stability method for the controller design |
Time invariance |
Time variance |
Dead time |
limitation Zung |
Non- linear |
MIMO | Remarks |
|---|---|---|---|---|---|---|---|
| Stability according to setting instructions (Ziegler-Nichols and others) |
Yes | - | - | - | - | - | Conditionally suitable for coarse adjustment |
| Bode diagram + Nyquist |
Yes | - | Yes | - | - | - | Phase edge recommendation: approx. 50 ° |
| Locus of the frequency response |
Yes | - | Yes | - | - | - | Critical point: (-1; j0) distance |
| Hurwitz criterion |
Yes | - | - | - | - | - | All coefficients a must be present and have the same sign. The "Hurwitz" determinants Di must all be> 0. |
|
Generalized Nyquist Criterion |
Yes | - | Yes | - | - | - | The transfer function determines: = number of poles with a positive real part, = number of poles on the imaginary axis. Change of angle |
| Root location method |
Yes | - | - | - | - | - | Root locus in the left half plane |
| Inverse Laplace transform |
Yes | - | - | - | - | - | Closed curve y (t), complex trigonometric calculation for vibration behavior. |
| State space State stability |
Yes | Yes | 1) | Yes | Yes | Yes | Good math skills required. |
| Numerical discrete-time methods: commercial programs or difference equations |
Yes | Yes | Yes | Yes | Yes | Yes | Closed course of the initial sequence . k = calculation sequence; Δt = discrete time, system parameters can be changed as required.
|
- 1) Only applies to discrete-time procedures in the state space model!
Controller design for linear time-invariant systems
The most important task of the controller from the point of view of the management behavior is the optimal controlled variable - i. H. quickly and with as little vibration as possible - to bring it to the level of the setpoint.
If the description of the controlled system as a linear time-invariant transmission system is available in the product representation, a suitable controller can be determined relatively easily . To simplify the open control loop , PT1 elements of the system are shortened against PD elements of the controller (pole-zero point compensation).
With the help of the equation for closing the control loop , the transfer function of the closed control loop results in a polynomial representation.
Thanks to the well-known results of the system analysis of transmission systems, the polynomials of the transfer functions of controlled systems or control loops can be represented relatively easily on three factorial basic forms using the zero point method (determination of the zero points of polynomials) (see article Control system # Characterization of the controlled systems ).
One of these three basic forms is the PT2 oscillation element, which always arises in regular systems with two or more PT1 elements with increasing loop gain of the closed control loop. The loop gain can be calculated from the desired degree of damping of the vibrating link. The value of the degree of damping decides whether the step response of the controlled variable is aperiodic , with damped oscillation or with increasing oscillation .
In controlled systems with non-regular systems (unstable T1 element) or unstable controlled systems with two I elements, the closed control loop with a suitable controller becomes stable with increasing loop gain.
Basic method of parameterization for an LZI controlled system
- The transfer function of a controlled system can be present as a polynomial in the denominator and numerator. It can be transferred to the product representation by calculating the poles and zeros.
- Dominant PT1 elements of the controlled system can be compensated by PD elements of the controller - if available, i.e. H. The same numerical values with the same sign of the poles and zeros therefore no longer have any effect. For the stability of the control loop, one more pole is required than there are zero positions within the transfer function.
- The dynamics of the controller must be adapted to the behavior of the controlled variable. If a control difference is allowed in favor of faster dynamics, an I element of the controller can be dispensed with.
- The loop gain must be determined so that the control loop can be closed .
- If there is no I element in the open control loop, it must be checked whether the manipulated variable , which can assume very high values, can be technically implemented due to the higher loop gain . If not, the transfer function of the open and closed loop does not apply to the large signal behavior. In this case, the transition behavior of the controlled variable after an input signal change is distorted and slowed down.
- With the closing condition of the control loop , an estimated value can be used for. This creates a denominator polynomial of a higher degree, corresponding to the number of poles of the open control loop. The difference to the open control loop is that the denominator polynomial of the closed control loop is normal form PT2 oscillation elements from a certain loop gain
- contains. The desired degree of damping can be determined by using different values of the loop gain .
- Any other poles in the s diagram that are removed from the pole pair of the oscillating element have little influence on the signal curve of the controlled variable . Any existing zeros only have an impact on the amplitude of the oscillating link.
Table of the transfer functions of the open and closed loop control
The table below with the "Open control loop" column refers to the product of the transfer functions controlled system and controller of the open (cut) control loop, in which pole-zero compensation has already been carried out and dominant PT1 elements of the system have been compensated.
The examples listed in the open-loop transfer functions column apply to many applications. If the parameters of the open loop are known, the transient behavior of the controlled variable for the closed loop can be determined by inserting . All factors of the individual transmission elements are summarized in the loop gain.
The first 3 application examples contain transfer functions of the open and closed control loop of the 2nd and 3rd degree.
Control loops of a higher degree (or substitute models with a dominant delay element and dead time element), depending on the distance between the dominant time constant and the remaining time constants of the controlled system, require ever further reductions in the loop gain so that the control loop shows a low overshoot amplitude for a desired transient response of the controlled variable. A low loop gain means a larger control difference. With an I element in the open control loop, the control difference in the static state is equal to zero; at the same time, this means a further reduction in the loop gain due to the additional phase shift. The loop gain is therefore often <1 if the controller or the system has an I component for a given control system of a higher degree - or with dead time.
Control loops with unstable components of the controlled system such as the unstable PT1 element or a controlled system with two I elements become stable with increasing loop gain in connection with a PD1 element.
For controlled systems with dead time, see section #Controller design for a model controlled system with dead time and dead time controlled systems
Note: The closed control loop is calculated numerically with the difference equations of the individual components and is simplified if the individual components of the open control loop are used and the closing condition is also implemented. The reasons for this are manipulated variable limits and dead time elements, which can not be described by transfer functions .
Design of a controller through pole assignment in the s-plane
The design process described below consists in assigning poles and zeros of a transfer function of a closed control loop to certain areas of the pole-zero diagram (see also pole specification in the state space) in order to define certain quality requirements. It is assumed that there is a dominant oscillation element ( PT2 element ), any additional poles that may be present are far enough away from the dominant pole pair in the left half-plane and therefore have little influence.
The task of a controller is now to fulfill the assigned position of the poles.
It is assumed that, in the ideal case, it is the 2nd order management transfer function with complex conjugate ( complex number ) poles. The general representation of the transfer function of the closed control loop as a PT2 element is:
- ; with and
The degree of damping (damping) is:
The overshoot time is defined as the time from the start of the input jump to the peak value of the first half-wave of the overshoot of the controlled variable . is thus a measure of the speed of regulation.
To determine the poles:
the denominator polynomial of the transfer function is transformed:
The variables and have the following influences on the vibration behavior of the controlled variable:
- Degree of damping
- determines the amount of overshoot of a step response. The overshoot is defined as the size of the peak value of the 1st oscillation amplitude to the stationary value of the controlled variable
- Real part of the pole pair
- The position of the real part of the pole pair in the left negative half-plane has no influence on the oscillation frequency, but determines the damping of the controlled variable .
- With an increasing amount of the real part with a constant imaginary part, the value of the damping increases , the overshoot amplitude and thus the overshoot amplitude decrease . The oscillation frequency remains constant. Therefore the overshoot time is also approximately constant.
- Imaginary part of the pole pair
- The size of the amount of the imaginary part with a constant amount of the real part determines the size of the amplitudes of the overshoots and thus the overshoot range .
- With an increasing imaginary part and a constant real part of the pole pair, the value of the damping decreases (worsens) , the overshoot amplitude increases and the overshoot time decreases .
- If the magnitude of the imaginary part is constant and the real part changes, the oscillation frequency is constant at different amplitudes.
- With and an angular range in the left half-plane can be defined, which specifies a constant damping for the amount of the imaginary part. For amounts .
- As the magnitude of the real part on the real axis and the imaginary part along the angular beam increases , the regulation becomes faster with constant damping. The reason for this is that large real parts of the pole pairs mean small time constants.
- If the absolute values and are the same, then the damping is always . This means an overshoot of approx. 5%.
- For pole pairs with the ratio of the absolute values and the degree of damping is . This means an overshoot .
Pole assignment strategy for a given open loop:
Initial situation: There is an open loop transfer function and the number of available PD elements (zeros) of the controller for pole-zero compensation has been used up. The transfer function of the open control loop of the 2nd or higher order (with I component) is given. The closed control loop should regulate the control behavior optimally, quickly and with few overshoots. Because in this case only the loop gain parameter is available, it is a matter of discretion whether to give priority to good damping or a short overshoot time .
- A value that represents a minimum system speed can be entered in the left half-plane perpendicular to the real axis . This absolute value for is dependent on the size of the time constants of the PT1 elements of the open control loop. The amount should not fall below this value. For a given open loop control and damping range, the margin for a minimum system speed is small. The only parameter is the loop gain .
- In the left half-plane, two angular beams are entered symmetrically to the real axis for the desired damping. It is recommended an angle range z. B. for a lower and an upper attenuation value, i.e. 4 angle rays.
- The open control loop is subjected to the closing condition with the loop gain parameter . The poles are determined for different values of . The easiest way to do this is to use a computer program to determine zeros from polynomials.
For the poles whose imaginary components lie within the permissible upper and lower angular range of constant damping, the associated loop gain can be selected and specified.
Conclusion: The controller design with the help of the pole assignment is a very interesting method. The somewhat laborious determination of the poles for 3rd and 4th order polynomials can be considerably simplified when using a computer. If, however, a computer is available, then when simulations with digital discrete-time computer programs are used, the closed course of the controlled variable can be calculated and graphically displayed as a function of a test input signal.
Controller design with the inverse Laplace transform
If the transfer function of a linear dynamic system or a closed control loop is given, the course of the output variable or the controlled variable can be calculated and graphically represented by means of the inverse Laplace transformation with a defined input test signal. A Laplace transformation table, which is available in every technical book on control engineering, is used, which represents the corresponding function in the time domain for many forms of product representation of a transfer function in the s domain.
The output variable of a dynamic system in the s range is:
The output variable of a dynamic system of the time domain for a transmission system in the s domain is:
Test signals for calculating the system response:
| Test signal | Time range | Test signal in the s range | System response |
|---|---|---|---|
| Impulse function | Normalized impulse = | Weight function | |
| Jump function | Unit jump for | Transition function | |
| Slope function |
Gradient: |
Ramp response |
The graphic representation of the step response (transition function) of a dynamic system is the most common representation of the system's time behavior. If the corresponding time function is found in the Laplace correspondence tables as a search term, the system behavior can be represented graphically for a given input signal by inserting different values .
Example of the application of the Laplace correspondence table for a dynamic system with real poles
| It should be noted that some correspondence tables in the s-area are defined in the pole-zero representation or the time constant representation. Gain factors are not transformed and are identical in the s-domain and time domain. Given: Transfer function for two PT1 elements connected in series: Input signal: step function U (s) = 1 / s Wanted: Time behavior of the system output variable : Solution: transition function (step response) The following equation for results from the correspondence table: |
Note: The use of the inverse Laplace transform requires a lot of computational work with trigonometric and exponential functions in damped oscillating systems.
Controller design using setting rules (heuristic methods)
The setting rules already carried out experimentally by Ziegler-Nichols in the 1940s relate to the step response of a controlled system and define it as a system with a PT1 element and a dead time element by creating a tangent at the turning point. In 1952, Chien, Hrones and Reswick extended the setting rules (rule of thumb (automation technology) ) for aperiodic behavior of the step responses of the controlled variable and for damped oscillating behavior with 20% overshoot. In addition, both groups are divided into leadership behavior and disruptive behavior. These setting rules are sometimes also referred to as rules of thumb.
The PT1-T t model controlled system defined as a substitute controlled system
Depending on the type and order of the original control system, it is only suitable to a limited extent with the specified setting data for parameterization. It is too imprecise as a model controlled system for optimizing a control loop.
Furthermore, this PT1-T t model controlled system is not suitable for LZI systems with a dead time.
See behavior of a control loop with a parameterized controller according to setting rules according to the graphic representation in the chapter "Controller design for a model controlled system with dead time"
Controller design for a model controlled system with dead time and dead time controlled systems
Since the knowledge of the so-called heuristic controller setting methods such as B. Ziegler-Nichols' concept of the "controllability" of an (imprecise) substitute controlled system with the ratio of rise time to substitute dead time . The "controllability" of this substitute controlled system is shown as difficult with an increasing substitute dead time in relation to the rise time. In fact, the regulation of a controlled system with a large dead time component is just as easy to regulate as with a small dead time component, but the dynamics of the control loop are unfavorable with increasing dead time. This can be remedied by controllers with special structures such as B. the method of Smith's predictor .
- Controlled system with pure dead time
If, in addition to PT1 elements, the controlled system contains a noticeable dead time t in relation to a dominant time constant , an I element is required within the control loop. A controlled system consisting of pure dead time can only - apart from special controllers - be controlled by an I controller.
The regulation of a controlled system with pure dead time with an I controller has a special feature that the loop gain
- ; with : any factor
at fixed leads to the same damping for all dead times . One chooses
the overshoot is approx. ü = 4%, which corresponds to a damping of approx. D = 0.7.
- Control path with dead time and further PT1 elements
It makes sense to use this relationship for controlled systems with PT1 and dead time systems, in which the controlled system is represented by a model with = equivalent dead time and 2 PT1 elements with the same time constants
is replaced. The associated controller is:
This model is suitable for a PID controller in that the two PD elements of the controller compensate the two PT1 elements of the controlled system model. It is also suitable for controlled systems with PT1 elements and dead time elements.
What remains is the transcendent transfer function of the open control loop
with for a damping of approx. D = 0.7.
This means that all the parameters of the controller for the model and for the real controlled system are known.
(See article Controlled system # Experimental identification of a controlled system with the help of a model controlled system ).
Control in the state space (overview)
See also chapter Control system in the state space
Control loop in the state space
The state space representation is one of several known forms of system description of a dynamic transmission system. It refers to a state space model, which mostly describes a scheme of the normal control form or the normal observation form.
The state space model symbolizes the n-th order differential equation converted into n-coupled first-order state differential equations. All relationships between the state variables (= state variables), the input variables and output variables are represented in the form of matrices and vectors.
The state variables of a linear dynamic transmission system describe the internal movement of the system. They physically represent the energy content of the storage elements contained in a dynamic system. They mean e.g. B. Voltage on a capacitor, current in an inductance, in a spring-mass system the potential and kinetic energy components.
According to the signal flow diagram of the normal control form , with the aid of the returned state variables, a dynamically advantageous state control loop can be formed, which can be simulated without a matrix display by means of numerical calculation of all signal quantities present.
Because the signal information of the state variables of the controlled system is available earlier than with the output feedback, the dynamic behavior of the control loop is better than a control loop with output feedback. With a state controller, high demands on the control quality can be met.
In practice, not all state variables can be measured for a given controlled system. Observers can remedy this by reconstructing the state variables if the route can be observed. The regulation in the state space is always an economic cost-benefit problem.
State controller in the state control loop
The basic principle of the state controller is the return of the internal information of the process, i.e. the return of the state variables. Therefore the state control can be seen as an extension of the principle of the cascade control.
Simulations of a state control loop can easily be carried out with a good model of the controlled system on a programmable computer. The description of the signal flow diagram of the controlled system and the controller in the state space can be done in the form of matrices as well as with the numerical time-discrete calculation. Depending on the order of the differential equation, all state variables are fed to a state controller which acts on the input of the state space model of the controlled system.
The linear state controller evaluates the individual state variables of the controlled system with factors and adds the resulting state products to a target / actual value comparison.
This state controller is not a P controller, although such an impression could arise according to the signal flow diagram. The state variables with evaluation factors fed back with the controller run through the arithmetic circuit once more to solve the differential equation with n integrators and form new circular variables, which results in differentiating behavior. Therefore, depending on the magnitude of order n of the differential equation of the system, the effect of the fed back state variables corresponds to that of a controller.
The pole assignment ( pole specification ) of the closed control loop is used as the design strategy for determining the evaluation factors of the state controller . Empirical settings of a model control loop are also easily possible. Because the integrators are connected in series, only the state variable x 1 (t) = y (t) is a stationary variable if the input variable is constant. All other state variables - assuming a stable controlled system - tend towards the value zero. After setting and optimizing the factor k 1 , a stable control loop with certain damping results with a proportional error compared to the controlled variable . The other factors of the state variables are set one after the other, for example to optimize the transition behavior.
A pre-filter before the target / actual comparison corrects the static error between and . By adding a higher-level PI controller, the disadvantages of the simple state controller disappear. The pre-filter is then no longer required.
Control loop with discontinuous controllers
Discontinuous controllers only have stepped output signals. These switching controllers are inexpensive to control the temperature, pressure and level of liquids.
The two-position controller has 2 states as a manipulated variable, for example ("On", "Off"). It is only suitable for proportionally acting controlled systems because this controller regulates a controlled variable to the required level by constantly switching it on and off. The switching frequency is reduced as the controller hysteresis increases.
The three-point controller has 3 control variable states. For example ("Forward", "Stop", "Backward"). It is used for integrally acting control systems such as motorized actuators.
Differences in the design strategy of continuous and discontinuous controllers
Continuous controllers are dimensioned so that the PD elements of the controller compensate for the PT1 elements of the controlled system. The desired transient response of the control loop is set via the P gain of the controller.
The time behavior of the controlled variable y (t) can be calculated algebraically for each Laplace-transformed input test signal w (t) using the transfer function of the closed control loop .
Continuous controllers behave linearly if no manipulated variable limitation occurs. A high P-gain and the PD elements of the controller always cause high manipulated variables. If the manipulated variables reach their physical limit in practice, the controller acts as a non-linear transfer element. Usual calculations with the transfer function are then no longer valid.
This behavior of the manipulated variable limitation does not occur in the case of a discontinuous controller . There are only known manipulated variables u (t) with the value U MAX , zero or -U MAX . The maximum reference variable w (t) of the control loop must always be smaller than the maximum manipulated variable U MAX of the controller.
Because the ideal two-position controller theoretically has an infinitely high gain, the switching frequency for the manipulated variable u (t) is automatically set in the control loop.
When designing the discontinuous controller for a control loop, the switching frequency and the settling behavior of the controlled variable are set by the parameters of the hysteresis , dead zone and time-dependent feedback.
Control loop with two-position controllers
For the functionality see controller # two- position controller .
The two-position controller is a very fast controller with very good dynamic properties. With a suitable feedback, an adapted electronic two-position controller can reduce the ripple of the signal of the controlled variable to less than 0.1% and compensate for static disturbances within the controlled system better than any other analog standard controller.
This advantageous behavior of the two-position controller in comparison to an analog standard controller occurs because the two-position controller always reacts immediately with the maximum available energy to every control difference. Depending on the size of the setpoint and the amplitude of the manipulated variable, which corresponds to a rectangular oscillation, the rate of increase of the controlled variable is different. For a given controlled system with the maximum manipulated variable U MAX , the various values of the reference variable are parts of the step response of the controlled system. (see picture: two-position controller for a first-order controlled system ).
For a jump in the reference variable, the period of change in the controlled variable from until the setpoint is reached is referred to as the rise time t ANR .
Overshoots in the event of a jump in the reference variable are avoided in that suitable feedback detunes the control difference in such a way that the manipulated variable is switched off prematurely.
Disturbance variables within the controlled system are compensated in time with the switching frequency. A static disturbance variable at the output of the controlled system has the same time behavior as with all other standard controllers. It corresponds to the behavior of the step response after a reference variable jump.
In comparison with continuous controllers, it must be taken into account that the two-position controller does not have a negative manipulated variable. With the manipulated variable zero of the two-position controller, the controlled variable runs exponentially to the value zero in accordance with the system behavior of the system .
Advantages of the two-position controller:
- Rapid increase in the controlled variable according to the step response of the controlled system,
- The system speed can be increased if, for example, the maximum manipulated variable U MAX is increased to a permissible value. This shortens the rise time t ANR .
- Fast correction when a disturbance variable is attacked within the controlled system,
- Control of large energies with low power loss,
- Only one polarity of an energy source is required,
- Simple specialist knowledge required for the operating personnel
Disadvantages of the two-position controller:
- There is always a slight residual ripple as an overlay of the controlled variable ,
- Slight overshoot of the controlled variable with a small setpoint .
- Since the step response of the controlled variable after a setpoint jump w (t) always follows excerpts from the step response of the controlled system, the system speed or the rise time t ANR is very different. The settling behavior of the controlled variable is optimized at the maximum setpoint.
- Radiation interference from electronic and mechanical switches must be taken into account.
- Mechanical switches are subject to wear.
Design strategy for a two-position controller with delayed yielding feedback (PID-like behavior)
- Record the step response of the controlled system
- The size of the input jump corresponds to the maximum manipulated variable U MAX of the controller. The reference variable must always be smaller than the maximum manipulated variable U MAX of the controller.
- Determination of the rise time t ANR for the maximum setpoint based on the transition function of the controlled system.
- The approximate rise time is determined by the time difference between the input jump U MAX and the value of the output variable of the controlled system, which corresponds to the maximum setpoint w (t). The actual rise time results in the closed control loop for the controlled variable under otherwise identical conditions.
- Determination of the transition function of the delayed yielding feedback:
- The transition function of the delayed yielding feedback is adjusted so that the pulse width at 1/3 above the base is about 10% larger than the rise time t ANR . If the pulse width is selected to be smaller, the manipulated variable will not be switched off prematurely when the controlled variable settles to the setpoint.
- The time course of the step response of the feedback results from the inverse Laplace transformation of the transfer function in the time domain.
- The standardized input jump 1 of the time-dependent feedback with the signal U MAX is:
- The output signal of the feedback u R with the two PT1 elements in differential circuit is according to the inverse Laplace transformation:
- The feedback signal u R (t) rises exponentially and then falls exponentially like a single sinusoidal pulse that becomes zero after a sufficiently long time. The size of the amplitude of the pulse and thus the influence of the feedback is set with the factor K R.
- Setting the hysteresis
- The hysteresis of the controller is particularly important for a first-order controlled system, because the switching frequency that occurs is too high. The switching frequency is reduced as the hysteresis influence u H (t) increases . For higher-order controlled systems, a setting of the order of magnitude 0.1% of the maximum system deviation e (t) is sufficient, because an increase in the oscillation frequency is usually necessary.
Behavior of a control loop with delayed yielding feedback from the controller
- The switching frequency of a control loop is increased by a negative-acting delayed yielding feedback.
- The trailing edge of the pulse of the delayed yielding feedback switches off the manipulated variable earlier after a setpoint jump and thus reduces the overshoot of the controlled variable.
- After the controlled variable has settled, the amplitude of the returned pulse decreases exponentially and becomes zero. So there is no permanent control difference.
- Each switching amplitude causes a small temporary detuning of the control difference at the output of the feedback. The desired higher switching frequency is thus retained.
- Without feedback, the controlled variable would slowly oscillate with a third-order controlled system with an amplitude of the order of magnitude ± 10% of the setpoint.
- With a suitable feedback, superimpositions of the controlled variable can be reduced to <0.1%. Noise-free measurement signal of the controlled variable required!
Control loop with three-point controllers
For the functionality see controller # three- position controller .
Three-point controller with three switching states have one input and two outputs and switch each of the two outputs to the "On" or "Off" or "both outputs off" state depending on certain small positive or negative values of the input signal . They allow two different types of energy to be switched and have a mostly symmetrical "dead zone" with an upper and lower limit value for the control difference , in which no switching activities take place around the zero point of the control difference.
Alternatively, instead of the two switches, three-position controllers have a positive and a negative manipulated variable with the values U MAX , -U MAX and a dead zone in which u (t) has the value zero as output variable u (t) .
Applications of the three-point controller
- Applications are often found in motorized actuators for flow and return and in all types of integrally acting control systems.
- In the case of proportional control systems with different dominant time constants (example: rapid heating up and slow cooling down), the reaction speed of the controlled variable for changes in reference variables can be improved if a cooling unit is switched on via a three-position controller instead of the two-position controller on a heating control system.
- Other applications of the three-point controller with an asymmetrical dead zone are known for reducing the fluctuation range of the controlled variable by regulating a base load with an applied partial load. Example: annealing furnace with two heating devices.
Draft of the three-point controller for a controlled system with a motorized actuator
The parameters of the three-position controller are:
- Hysteresis: U H to reduce the switching frequency.
- Dead zone ± E TOT as a function of a small part of the control difference, in which the output variable of the controller u (t) = zero is controlled.
- Manipulated variables U MAX and -U MAX .
- delaying returns u R (t) if needed.
Influence of the hysteresis
- The hysteresis is created by positive feedback of the signal of the manipulated variable u (t) via a coupling factor K H to the input of the controller e (t) .
- Positive:
- Negative:
- As the influence of the hysteresis increases, the switching frequency of the control loop is reduced. In the case of integral control systems with delays (PT1 elements), the size of the hysteresis is no longer relevant because the switching frequency is slow due to the delays. The hysteresis should be kept as small as possible.
Behavior of the dead zone
- The dead zone ± E TOT refers to the range of a positive and negative criterion of the input signal e (t), in which the output variable of the three-point controller u (t) is controlled to the value zero. A symmetrical dead zone is assumed. The positive and negative dead zone can be defined in% of the maximum control difference e (t).
- If the two criteria of the positive and negative area of the dead zone are equal to zero, the behavior of the three-position controller changes to that of a two-position controller.
- On an ideal integral controlled system without delays, without hysteresis and without signal noise, an extremely small dead zone is sufficient to control any controlled variable with great accuracy without vibrations.
- On an integral controlled system without delays, the control variable of the controller is switched off prematurely as the dead zone increases with a positive jump in the reference variable w (t). The controlled variable therefore does not reach the setpoint.
- In a real integral controlled system with delay elements (PT1 elements), in the event of a positive jump in the reference variable w (t), the controlled variable y (t) continues to increase despite the manipulated variable being switched off until the memories of the delay elements are empty.
- Both effects of the premature deactivation of the controlled variable by the dead zone and the lag of the controlled variable due to the energy storage of the delay elements can be compensated for by a simple mathematical relationship.
- The size of the design of the dead zone depends on the time constants T of the delay elements (PT1 elements), the maximum manipulated variable of the controller ± U MAX and the integration constant T N of the motorized actuator. If there are several delay elements, the time constants are combined additively if the accuracy is good.
- Dead zone for integral controlled systems with PT1 elements:
Numerical calculation of dynamic transmission systems (overview)
Relatively simple transmission system structures with non-linear elements can no longer be solved in a closed manner by conventional calculation methods in the continuous time domain. With commercially available personal computers, the behavior of any meshed system structures can be carried out relatively easily by means of numerical calculation.
Commercial programs
For the implementation of the calculation of transmission systems or the simulation of control loops, commercial computer programs are available. With the most popular programs such as MATLAB and Simulink , extensive instruction sets are available for the theoretical modeling of dynamic systems and many special control commands. See also Control engineering # Tools for rapid prototyping in research and development . The most important software tools for computer-aided analysis, design and rapid control prototyping of regulations are listed there.
Alternatively, you can use your own computer programs to perform very efficient control loop simulations using difference equations in conjunction with logical operators. Relatively little mathematical knowledge is required.
Advantages of simulating systems with difference equations
- Simple math requirements through algebraic operations
- Treatment of combined LZI systems with non-linear systems
- Entry of initial values possible
- Representation of a control loop as a block diagram with entry of the difference equation and logical operators
- Handling of multi-loop systems (MIMO systems)
- System descriptions using differential equations in the state space in the form of the normal control form can also be replaced by difference equations. The calculation of a state control loop is relatively simple because only integrals have to be solved.
- With a tabular representation of the individual calculation results, a complete view of the inner system movement sequence of the control loop. When using the spreadsheet, immediate graphic representation of the calculation results using available tools for the system time curves.
Basic method of numerical calculation of a transmission system
The application of the numerical computation of a linear transmission system according to the Euler square method relates to algebraic operations with difference equations that can be derived from differential equations of linear elementary systems. Arbitrarily meshed linear system structures are composed of a maximum of three non-decomposable elementary systems of a transfer function in the numerator and denominator. The Laplace variable corresponds to the complex frequency.
If the numerical values of the coefficients of a transfer function in the polynomial representation are known, the factorial representation in linear factors can be obtained with the help of the decomposition of zeros in the numerator and denominator of the transfer function. The zeros of the numerator and denominator polynomials can each have the value , (real) or (conjugate complex = systems of the 2nd order) depending on the numerical values . This results in three types of linear factors that have a total of 6 special forms of behavioral properties in the numerator and denominator of the transfer function in the time domain, each of which can occur singly and repeatedly.
With the help of the difference equations of the associated first order transfer elements, all linear systems of higher order - including systems with conjugate complex poles - can be simulated. It is easy to simulate a second order difference equation using a model of an auxiliary control loop with a PT1 element and an I element. In general, a higher-order difference equation can be set up whose differentials by difference quotients are replaced higher order.
Due to different methods of approximation (approximation) to a time-dependent function, different difference equations exist for the same function. The simplest method is the Euler rectangle method. All difference equations relate to the dynamic system to be described . The current time is .
As a consequence , the listing of finite, consecutively numbered numbers is understood here. can be any number in the sequence. A calculation of the sequence (for first-order difference equations) is a calculation one sequence behind. The consequence is the current state and the consequence is a future state. Recursive algorithms of the difference equations always calculate the output variable of a system from the output variable of the sequence and the current sequence for the time interval .
The most understandable type of representation of a numerical calculation of a dynamic system with finite subsequent elements is always in tabular form for a limited time range.
Each line with the results of difference equations and the time from to and the input variable is calculated for the same time interval and still relates recursively, depending on the order, to a previous result or to several previous results.
Because of the high degree of familiarity, these transfer functions (linear factors) are related in a time constant representation to the difference equations shown below using the associated differential equations.
Associated difference equations of first order transmission systems G (s):
| Elementary systems | I-link | D link | PD 1 link | PT 1 link |
|---|---|---|---|---|
| Transfer function | ||||
| Difference equations (after Euler) |
(With K = gain factor, = current output variable, = previous output variable, T = time constant, = current input variable)
Nonlinear systems or dead time systems can be taken into account as a table column or by means of logical commands. Initial values of the transmission systems with energy storage can be treated according to the normal control form of the state space representation.
A simple procedure is described below that leads to efficient results and clearly shows the internal system movement sequence, even for complex control loop structures.
Simulation model of a dynamic transmission system
With the simulation of a mathematical model of a transmission system or a control loop, it is possible to carry out a system analysis or a system optimization with suitable test signals .
The advantage of simulating on a model is obvious. No technical systems are endangered or required, the time factor does not matter, very fast or very slow processes can be optimized. The prerequisite is the mathematical description of a well-approximated model of the mostly technical controlled system.
The model ( modeling ) of a transmission system is the mathematical representation of a mostly technical (possibly physical, chemical, biological) facility. It is obtained analytically using differential equations or experimentally using identification methods.
The modeling of an existing hardware control system or control system in the time domain is done experimentally in the simplest form by graphically recording the step response with subsequent analysis of the behavior over time. (See Experimental System Identification )
The modeling in the frequency domain is done by stimulating the system with a variable frequency and recording the output amplitude and phase. The transfer function of the system is formed via the frequency response.
Nonlinear systems cannot be described by transfer functions. This can be done relatively easily using time-discrete descriptions in the form of logical commands (e.g. for signal limitations) or using a table for a non-linear characteristic curve.
- → For full details, see article Difference Equation .
Extended control loop structures
Decentralized regulation
The decentralized control is a special approach for the control of multi-variable systems with the same number of inputs and outputs. Each controlled variable is assigned an input that has the greatest possible influence on the controlled variable. A single variable controller is designed and implemented for each pair of inputs and outputs, i.e. single variable control loops.
With decentralized control, the procedure is as if the control loops would not influence each other and any existing couplings from other control loops (shown in dashed lines in the figure) are considered as disturbance variables for a control loop. The procedure therefore works particularly well when the cross-couplings in the controlled system are small. Various coupling dimensions were developed for their evaluation . If the couplings cause excessive undesirable influences on the control loops, special techniques can be used to compensate for them. A decoupling network is often used, which is placed in front of the line, and together with this creates a system without cross-coupling, for which the approach of independent single-variable control loops really applies. In this case, one speaks of decoupled control.
Cascade control
For the cascade control it is assumed that the controlled system with its subsystems has a chain structure and that input interfaces for the control difference and output interfaces can be formed with measuring devices for the auxiliary controlled variables.
The principle of cascade control consists in the hierarchical nesting of control loops. First, auxiliary control variables are controlled with fast inner control loops, the setpoints of which consist of the manipulated variables of the outer, slower loops.
A common goal of cascade control compared to a standard control loop is the rapid suppression of interfering signals within the fast-reacting system subsystems before the interfering signals reach the output of the overall controlled system. The outer control loop receives an I component to minimize the static control difference.
Smith Predictor
A predictor uses the knowledge of the controlled system model directly (not indirectly as with an observer ) to predict future controlled variable curves. This offers advantages in particular in systems that are heavily affected by dead time , since conventional controllers can then usually only be set very carefully. Examples of long dead times can be found, for example, in process engineering when substances are transported over long lines. In order to enable a much more aggressive regulation of these systems, the Smith predictor was developed in the 1950s.
The Smith predictor makes a prediction of the future course of the controlled variable using a parallel model contained in the controller. For this task, the dead time affected and the dead time free part are considered separately. The controller is then not set on the actual controlled variable , but on the prediction without dead time . This allows the controller to be set much more aggressively. Up to this point it is a control ; In order to enable an adaptation to model errors and disturbance variables and thus to a control, the predicted value is compared with the real value and is thus included in the control. If the controlled system model agrees well with the controlled system, extremely good control behavior can be achieved by the control loop with Smith predictor, because the control variable curve is determined as if there were no dead time. The disturbance behavior is in principle worse because no a priori knowledge about the disturbance variable can be used.
The control loop with Smith predictor is, however, not very robust with regard to errors in the controlled system model, in particular with respect to errors in the dead time. This greatly restricts its use, since in practice it must usually be assumed that the control system parameters will have a relatively high degree of inaccuracy over the course of the service life of the control loop (e.g. due to aging, other environmental conditions, etc.). The lack of tracking of the model state to the route state can result in further problems with non-linear routes, as the occurrence of disturbances can cause the route condition and the model state to diverge and the plant model is then at a different operating point than the route. Another disadvantage of the Smith predictor is that it can only be used on stable controlled systems.
With increasing speed of computers, it becomes possible for ever faster running processes to carry out simulations and model adaptations and optimizations taking place in real time, whereby a number of different model predictive control methods, such as e.g. B. Model Predictive Control , especially in the chemical industry.
Split-range control
The split-range control concerns the implementation of a manipulated variable by several actuators with a limited effective range. For example, both an electrical heater and a cooling coil through which a cooling medium flows are used to regulate the temperature in a batch reactor. A positive control signal can be achieved by controlling the heater plugs. A negative control signal, on the other hand, means the request for cooling, so that the heating must be switched off and a valve opened instead to release the cooling medium.
Feedforward control
Usually, disorders are by their nature unknown. However, if a measurement or estimate of the disturbance is available, this can be used by adding it to the control loop in order to improve the disturbance suppression.
An example of measurable disturbances is the outside temperature in room temperature controls. It is used in heating systems to adjust the flow temperature.
One way of estimating disturbances is to use a disturbance variable observer .
Pilot control and pre-filter
Feedforward
Single-loop standard control loops allow the behavior of the controlled variable to be optimized for either the command or disturbance behavior. This property is called a "degree of freedom".
By changing the control loop structure you can z. B. achieve an independence of the command and disturbance behavior by a pre-control or a pre-filter. This property is called a control loop with two degrees of freedom.
A control loop with a feedforward control allows the management behavior to be improved with the following properties:
- The feedforward control does not influence the disturbance behavior.
- It has no influence on the loop gain and therefore does not endanger the stability of the control loop.
- The feedforward control as pole-zero point compensation of the controlled system only has a model character in practice. Implementation is difficult because the differentiating elements required in the analog hardware solution require parasitic delays, and in the digital software solution very high actuating amplitudes arise. Both methods reduce the desired effect. Remedy: Conversion into a pre-filter or division of the controlled system into several control loops (e.g. cascade control ).
Transfer function of the feedforward control with G s (s) as a function of the controlled system:
The transfer behavior of the precontrol corresponds to the reciprocal of the transfer function of the controlled system. It is fed by the reference variable W (s) and intervenes with U vs (s) additively on the input of the controlled system U (s) without changing the disturbance behavior.
There are limits to the implementation of the feedforward control in order to compensate for the transfer behavior of the feedforward control with the controlled system to a factor of 1.
- The feedforward control of a controlled system with z. B. 3 PT1 elements requires a prefilter with 3 PD elements.
- A threefold differentiation of the reference variable W leads to very high manipulated variables and thus to unavoidable limiting effects that oppose the desired effect.
- Additional small delay elements in the feedforward control worsen the desired effect considerably. This means that the implementation of PD elements with analog methods is not possible due to the inevitable parasitic time constants.
The remedy is to convert the feedforward control into a prefilter with the same dynamic properties affecting the control loop. Instead of the precontrol, a prefilter is used upstream of the control loop, which is fed by the reference variable . The prefilter receives the inversion of the transfer function of the closed control loop (without precontrol).
Pre-filter
A prefilter is a function block with the transfer function:
The filter is in front of a control loop and is fed by the reference variable . There are no other uniform definitions.
Pre-filters can have the following functions:
- As a correction factor for a control loop without an I component for fixed value controls. The remaining static control difference is corrected.
- Delay elements (PT1 element) or linear rise limits can be used to avoid setpoint jumps.
- In the case of controls with actuators with non-linear behavior, approximate linearizations can be carried out.
- Pre-filters for target trajectories allow the time-controlled reference variable to be dynamically adapted to the control behavior of the control loop with regard to minimal consequential errors.
- Pre-filter for the steady-state control accuracy in state controllers.
- Pre-filters contain the function of pre-control to improve the control behavior with optimized disturbance behavior.
The following generally applies: With single-loop control loops, any poles, complex conjugate pole pairs or zeros of the control loop (without a prefilter) can be compensated for with a prefilter.
Conversion of the behavior of a pre-control to a pre-filter
The transfer function of the feedforward control is for the ideal case:
as an inversion of the controlled system. The product of feedforward control and controlled system is compensated to 1.
The conversion of the transfer function of the feedforward control G VS (s) for the same behavior of the prefilter G VF (s) is calculated as follows:
This relationship is the inversion of the closed loop transfer function. If the pre-filter is upstream of the control loop and the filter is fed by the reference variable W, then the control behavior of the control loop is theoretically infinitely fast.
This behavior is easy to understand because it is a pole-zero compensation. The transfer function of the control loop always contains PT2 elements with conjugate complex poles when optimizing the disturbance behavior. To compensate for this, a PD2 element with conjugate complex zeros is required. It generally applies to a control loop or a control system that the behavior of an oscillating element (PT2 element) can be completely compensated for by a PD2 element with complex conjugate zeros if the parameters of both systems are identical.
PD2 terms with complex conjugate zeros are obtained by subtracting the mean term of the transfer function from the transfer function of a PD2 term for a specific D term.
This transfer function can be implemented using hardware or software.
For more information on the implementation of a PD2 element with conjugate complex poles, see the article “Controller”, main chapter “ Continuous controller ”.
Advantages of the prefilter compared to a pilot control:
- Pole-zero point compensation : The product of the transfer functions of the prefilter and control loop acts as pole-zero point compensation. Delay elements (parasitic PT1 elements) can be added without restrictions, which determine the transition behavior of the controlled variable without influencing the compensation of the complex conjugate poles and zeros.
- Transfer function of the product pre-filter and control loop:
- Normal actuating amplitudes : As the size of the delay elements increases, high actuating amplitudes are reduced to normal values.
- Fewer PD elements: By choosing a suitable controller, the order of the transfer function of the control loop can be reduced by one order compared to the controlled system.
- Oscillation element with dead time: Compensation of the oscillation element of a control loop with a PD2 element in the pre-filter is also possible if the control loop contains a dead time. The dead time cannot be compensated in this way.
Examples of control loops outside of technology
In addition to technology, the term control loop is also used in biology , especially in zoology , in order to clearly represent physiological processes. An example of the regulation of such functions is the homoiostasis of the hormonal system , which can be demonstrated particularly impressively by the regulation of the blood sugar level by the hormone insulin . It is therefore not just a purely technical model, but a general organizational principle that can also be understood under terms such as self-regulation and systems theory .
Biological control loops
In biology one finds a multitude of control loops, both relatively simple and more complex on a physiological level within the organ systems of higher living beings, which contribute to their homeostasis , up to the highly complex control loops within communities on the ecological level . Examples:
- End product inhibition in the synthesis of amino acids within cells and tissues.
- Regulation of the water balance in plants
- Regulation of breathing (a humoral control circuit based on chemoreceptors)
- Regulation of the oxygen content of the blood
- Thermoregulation : Animals of the same temperature need a certain body temperature in order to survive , which varies within a tolerance band, but should not leave it. The nervous system of every animal at the same temperature therefore contains a temperature control circuit with appropriate receptors as sensors and sweat glands and muscles as actuating devices.
- The kidneys regulate the water balance and the acid-base balance
- Pulse regulation: In order to supply the cells with sufficient oxygen and energy, sufficient blood circulation is required, which depends on the physical strain. This takes care of u. a. the regulation of the heart rate by the autonomic nervous system .
- Blood pressure regulation: If the blood pressure is too low , there is insufficient blood circulation and the cells cannot be supplied with oxygen and energy. Too high blood pressure damages the organs. That is why there is blood pressure regulation in animals and humans.
- Regulation of the amount of incident light into the eye by enlarging or reducing the pupil and adapting other sensory organs ( Weber-Fechner law ).
- Regulation of the blood level of numerous hormones (e.g. in the thyrotropic control circuit )
- Regulation of food intake through hunger and satiety
- Regulation of the blood sugar level : The blood sugar ensures the energy supply of the organism and is adapted to the physical strain.
- Regulation of population density through predator-prey relationships
See also: biocybernetics
Economic control loops
From the field of economics the following should be mentioned:
- Pricing in markets
- Market regulation by the state.
- Cobweb theorem , pig cycle
Management-oriented control loops
- Control loop of corporate management
- Control loop of personnel management
Quality circle
From the area of quality management there is the quality group , on which quality management systems are based in accordance with the DIN EN ISO 9001 : 2015 regulations.
Linguistic control loops
The article linguistic synergetics shows that quantitative linguistics has developed control loops on different language levels ( morphology (linguistics) , writing , syntax and others), some of which also work beyond the language levels or connect them with one another.
See also
- Portal: measurement, control and regulation technology
- Systems theory (engineering sciences)
- cybernetics
- Autopoiesis
- stabilization
Web links
- The Smith Predictor MathWorks (MATLAB)
- Excel table with control elements and control loops in the PyConSys project folder on GitHub
literature
- Gerd Schulz: Control engineering 1: linear and non-linear control, computer-aided controller design . 3. Edition. Oldenbourg, 2007, ISBN 978-3-486-58317-5 .
- Manfred Reuter, Serge Zacher: Control technology for engineers: Analysis, simulation and design of control loops . 12th edition. Vieweg + Teubner, 2008, ISBN 978-3-8348-0018-3 .
- Günter Ludyk: Theoretical control engineering 1. Basics, synthesis of linear control systems . Springer, Berlin 1995, ISBN 3-540-55041-0 .
- Günter Ludyk: Theoretical control engineering 2. State reconstruction, optimal and non-linear control systems . Springer, Berlin 1995, ISBN 3-528-08911-3 .
- Jan Lunze: Control engineering 1: System theory basics, analysis and design of single-loop controls . 7th edition. Springer, 2008, ISBN 978-3-540-68907-2 .
- Heinz Unbehauen: Control engineering I: Classical methods for the analysis and synthesis of linear continuous control systems, fuzzy control systems . 15th edition. Vieweg + Teubner, 2008, ISBN 978-3-8348-0497-6 .
- Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Europa-Lehrmittel, Haan-Gruiten 2019, ISBN 978-3-8085-5869-0 .
Individual evidence
- ^ Otto Föllinger: Control engineering . 5th edition. Hüthig, 1972, ISBN 3-7785-1137-8 , pp. 13 .
- ^ Author: Manfred Reuter / Serge Zacher: Control technology for engineers; Main chapter: Digital control.
- ^ Author: Manfred Reuter / Serge Zacher: Control technology for engineers; Main chapter: Description of control loops with transfer functions.
- ↑ Author: Lutz / Wendt: Pocket book of control engineering; Main chapter: Transfer function of control loop elements.
- ^ Author: Manfred Reuter / Serge Zacher: Control technology for engineers; Main chapter: Control devices, sub-chapter: Dynamic requirements.
- ↑ Author: Lunze: Regelstechnik 1; Main chapter: The control loop; Subchapter transfer function of control loop elements.
- ^ Author: Manfred Reuter / Serge Zacher: Control technology for engineers; Main chapter: Design of linear control loops, sub-chapter: Quality criteria of the time behavior.
- ↑ For definition of rise time, see specialist literature: Lunze / "Regelstechnik 1", Lutz - Wendt / "Taschenbuch der Regelstechnik" and Heinz Unbehauen / "Regelstechnik 1".
- ^ Author: Manfred Reuter / Serge Zacher: Control technology for engineers; Main chapter: Non-linear elements in the control loop.
- ^ H. Lutz, W. Wendt: Pocket book of control engineering with MATLAB and Simulink, chapter: Laplace transformation .
- ^ H. Lutz, W. Wendt: Pocket book of control engineering with MATLAB and Simulink. 2019, Chapter: Regulation through state feedback
- ↑ M. Reuter, S. Zacher: Control technology for engineers. 2008, chapter "Two-point controller with feedback".
- ↑ Gerd Schulz: Control engineering 1. 2007, chapter "Two-point controller with hysteresis and feedback".
- ↑ M. Reuter, S. Zacher: Control technology for engineers. 2008, chapter "Three-point controller".
- ^ OJM Smith: A Controller to Overcome Dead-Time. In: ISA Journal. & (1959), No. 2, pp. 28-33.
- ↑ D. Abel, A. Bollig: Rapid Control Prototyping. Springer-Verlag, Berlin / Heidelberg 2006, ISBN 3-540-29524-0 .
- ↑ A. Steinkogler: A new predictor controller for regulating systems with dead time. In: Automation technology. 44 (1996), No. 4, pp. 171-179.
- ↑ Erich von Holst , Horst Mittelstaedt : The Reafferenzprinzip. In: The natural sciences. 1950, 37.
- ^ Norbert Wiener : Cybernetics: or control and communication in the animal and the machine. 1948.
- ^ H. Ulrich: The enterprise as a productive social system. 2nd Edition. Bern / Stuttgart 1970.
- ^ HJ Rahn: Compact personnel management. A system-oriented approach. Munich 2008.










![{\ displaystyle y (k) = y (k-1) + f \, [u (k), \, system]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140a5613af62de04238f567f08aca7501f19c124)




![{\ displaystyle y (k) = y (k-1) \, + f \, [u (k), \, \ Delta t, \, T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a3357e7cf11cec7727fc8d5e524aee4843d76e3)




















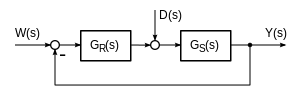



































































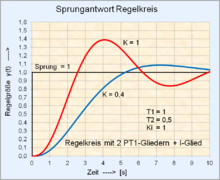




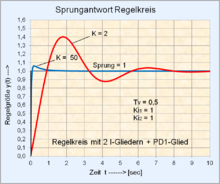





























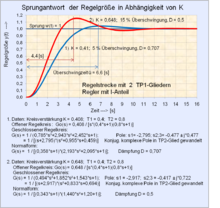














![y (t) = {\ frac {1} {a \ cdot b}} \ cdot {\ bigg [} 1 - {\ frac {b} {ba}} \ cdot e ^ {- a \ cdot t} + { \ frac {a} {ba}} \ cdot e ^ {- b \ cdot t} {\ bigg]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd418692b7dd65d36773cb7bf5d8eb86b630304e)


















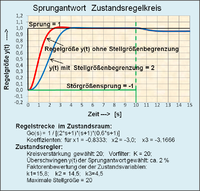





![{\ displaystyle u_ {R} (t) = K_ {R} \ cdot U_ {MAX} \ cdot [(1-e ^ {- {\ frac {t} {T1}}}) - (1-e ^ { - {\ frac {t} {T2}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fffb7ef3cd9f98840364b651df29987ef2da4632)

























![{\ displaystyle = [u _ {(k)} - u _ {(k-1)}] \ cdot {\ frac {T} {\ Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5c739a81b824897986be87ecb7e7f74a712af9f)
![{\ displaystyle = K_ {PD1} \ cdot [u _ {(k)} + [u _ {(k)} - u _ {(k-1)}] \ cdot {\ frac {T} {\ Delta t}}] }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e8013fa68abe744c128b654cd7d737774534cf)
![{\ displaystyle = y _ {(k-1)} + [K_ {PT1} \ cdot u _ {(k)} - y _ {(k-1)}] \ cdot {\ frac {\ Delta t} {T + \ Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83f1f8a8ae63d4def6148099bc1a4442a2788d6d)



















