Control technology

Control engineering includes the design and implementation of controls , that is, the targeted influencing of the behavior of technical systems ( devices , apparatus , machines , plants and biological systems ). Like control engineering , it is a branch of automation engineering . Controls are divided into binary , analog and digital controls.

In binary controls , the input and output variables of the control devices are binary . The system to be controlled (control path) is influenced by the binary output variables of the control using the actuators . Examples of actuators are a light , a valve or a motor . The binary input variables of the control are operating signals from people and feedback signals from sensors in the control line, for example the switch position (on / off), the valve position (open / closed) or the state of motion of the motor (rotating / standing). For example, lighting , a water flow or the movement of a vehicle drive are controlled .

In the case of binary controls, a distinction is made between logic controls and sequence controls . In the case of sequential controls, relevant values ​​of the control variables are reported back to the control input by means of sensors. If, on the other hand, there is no feedback, one speaks of logic controls whose mode of operation is binary or multi-valued.

Characteristics of the information processing in the binary complex controls are contained in the control program logic operations between the input signals (including the confirmed signals from the sensors). The description and calculation of binary controls can therefore be carried out by means of binary mathematics.

In analog controls , the input and output variables of the control device are analog signals ; these controls have no feedback. An example of an analog control is the constant change of a lever position when turning a cam plate on which the lever is applied. Analog controls can be described as closed-loop control using differential equations.

A controller is called a digital controller if it processes digital signals . Digital signals are multi-bit signals, the individual bits of which are part of a coded information representation. To process digital signals, control commands with byte or word operands, so-called word instructions, are required.

Today most of the controls are binary or digital , with the sequence controls by far predominating (several control variables are influenced one after the other). You have several or even many inputs and outputs. In addition to the start signal as well as other control signals, the input signals do not originate from the operator, but from the control track, and are equipped with sensors detected and reported back ( feedback ) states of the control variables. The respective subsequent step in the process is only carried out when the previous step has been completed. This means that there are consecutive closed sub- control loops which, however, should not be confused with the non-subdivided closed control loop . Its purpose is a technical "self-correction" of the controlled variable that takes place in the event of malfunctions. Controls that are also designed to protect against interference cause the process to be controlled to be transferred to a safe state or switched off if the control values ​​are dangerous.

To cope with the complexity of modern controls, there are special methodological aids in the form of various theoretical models and corresponding computer-aided tools for their design . Such tools are also used for simulation, planning, configuration, programming and service (error diagnosis, maintenance and repair).

History of control technology

Perforated tape control on a historic jacquard loom

Historical roots

Historical examples

• The Greek inventor Heron of Alexandria (approx. 20–62 AD) describes in his work "Automata" a door control in which the temple door opens by lighting a fire (continuous control), also automatic theater that is controlled by itself unwinding ropes could perform various movements. He also designed a holy water machine that dispensed a small amount of consecrated water after inserting a coin. However, these ideas have been forgotten over time and have not been further developed.
• At the beginning of the 18th century music boxes were controlled by pin rollers. In the middle of the 18th century, weaving machines were controlled by wooden punched cards, which Joseph-Marie Jacquard significantly improved in 1805 with a circular perforated belt.

Time table for components and devices of control technology

• In 1835 Joseph Henry invented the electromechanical relay.
• In 1947 the transistor was invented in the USA.
• 1954 the first numerical control with electron tubes is produced.
• In 1958, the electronic component system is SIMATIC the company. Siemens for binary control systems on the market, which is composed of discrete components such as diodes, transistors and resistors.
• 1969 Richard E. Morley invents the programmable logic controller (PLC) at the US company Modicon (type Modicon 084). At the same time , Odo J. Struger from Austria developed a corresponding PLC at the US company Allen-Bradley .
• 1970s: The programmable logic controller (PLC) replaces individually built electronic, pneumatic and relay controls.
• In 1971 the microprocessor was invented in the USA. Since 1975 he has been increasingly penetrating PLC technology and has continuously expanded its performance and flexibility to the present day.

Control technology and industrial development

The important role of control technology in industrial development is also evident in the future Industry 4.0 project of the German Federal Government and Industry, with four stages of the industrial revolution being distinguished:

• Stage 1
  beginning in 1784 with the use of mechanical looms , in particular by wooden punch cards - controls were and later developed by controllers with circumferential bands for textile machinery.
• Stage 2
  start 1870 to the first use of production lines in the United States (slaughterhouses of Cincinnati ) using electric drives, by respective contactor - and relay - controls were switched.
• Stage 3
  Beginning in 1969 with the first programmable logic controllers from the US company Modicon (type Modicon 084, inventor: Richard E. Morley ), which marked a breakthrough in industrial electronics and information technology for mass control and automation of production.

• Stage 4: Industry 4.0
  beginning of 2012 with the development and use of so-called cyber-physical systems (CPS) with global networking for the globally optimized control of internationally organized production ( Internet of Things ). This step-by-step transition from the third to the fourth stage has been made increasingly accessible to a broader public since 2013 with the Hannover Messe .

History of the standardization of control terms

The theory of control technology has lagged behind that of control technology to this day , which is reflected, among other things, in the inadequate standardization and definition of relevant terms.

The DIN standardization has for many years between regulation as a closed circuit and control than open chain distinguished. Since there are also closed sub-circles in digital control technology, the control system was redefined in 1994 in the third, currently valid edition of DIN 19226 ( regulation and control technology , replaced unchanged by DIN-IEC 60050-351 since 2002): “Identification for controlling is the open path of action or a closed path of action, in which the output variables influenced by the input variables do not act continuously and again via the same input variables on themselves ”. The subordinate clause is essential ... the output variables influenced by input variables do not act continuously and do not act on themselves again via the same input variables . The comparison of open or closed action path (control) to closed circuit (control) has contributed more to uncertainty than to clarification.

Standards for programming the programmable logic controllers

In the control standard DIN 19237, the various types of program implementation using connection-programmed and memory-programmable controls have already been classified.

The DIN 19239 standard : "Measuring, controlling, regulating - control technology - memory-programmed controls - programming" was created by the German Commission for Electrical, Electronic and Information Technologies . The first draft was published in 1981 and replaced by a released version in 1983. DIN 19239 defines three programming languages ​​for controls:

• Instruction list (STL),
• Ladder diagram (LAD),
• Function diagram (FBD).

DIN 19239 was withdrawn in 1994 and replaced by a DIN based on the identical European standard DIN EN 61131-3 . In addition to the three mentioned, two further programming languages ​​are included, so a total of five:

• Sequential Function Chart (SFC, Sequential Function Chart)
• Structured text (ST).

The resulting international standard IEC 61131-3 (also IEC 1131 and 61131) is the only globally valid standard for programming languages ​​for programmable logic controllers.

Nature of binary controls

According to DIN 19226, 3rd edition 1994, part 1 or DIN IEC 60050, part 351, binary control or binary control is a process in a system, consisting of a control device and a control path, in which one or more process variables in the Control path, which are referred to as control variables, can be influenced by binary output variables of the control device (also called control signals) in accordance with a predetermined control algorithm (control program).

Signals in binary control systems

The input and output variables are binary signals. These are discrete-value quantities, the information parameters of which can only have two values, denoted by 0 and 1.

In the case of binary input signals, a distinction must be made between operating signals that are entered via operating devices such as switches or buttons and binary measurement signals that are recorded by sensors (such as end position switches or light barriers).

From the binary input signals of the control means the control algorithm can be formed by logically combining the output signals of binary control signals accordingly, which actuators (also called actuators referred to, eg. Relay switch, switching contactor, solenoid valve or motor) to the control object ( technological process, control path) and thereby change control variables (outputs of the technological process).

The control variables can either be discrete-value variables (e.g. signals for switching lighting on and off by means of a two-way or cross-connection) or analog , i.e. H. variables that are continuous in value and time (e.g. temperature, pressure, level, distance, angle, speed).

The signal flow in control systems can have two different basic structures:

• Open control chain , whereby the sensors take their information (measurement signals) from the environment, but not from the technological process (control path),

• Closed control circuit , whereby the sensors take their information (feedback: binary signals) from the technological process (sequence control).

Control types

Control system with display of signals, types of control and the associated operation and programming

• Link control

• flow control

The majority of all types of control in practical applications are the sequence controls. A distinction is made here between process-controlled and time- controlled sequence controls .

In addition to "logic and sequence controls", there are also controls in which no sensor signals (i.e. no feedback) are included and which only process a schedule (time program) or route plan (route program) via their outputs and the downstream actuators:

• Time program control: sequence of events according to a specified schedule, e.g. B. at a simple traffic light

• Route program control: sequence of events according to a specified route plan, e.g. B. in a copy milling machine or copy lathe.

As open controls (program controls), these schedule and route plan controls make up a relatively small proportion of all control types.

New approaches to the description of the operational sequences of logic and sequence controls

Since around 1995, attempts have been made in the specialist literature to describe control more precisely, on the one hand to show its relationship to control more clearly and, on the other hand, to more clearly differentiate the different types of control from one another: Zander , Töpfer (1996), Lunze (2003), Langmann (2004) , Litz (2005), Heimbold (2015).

By Wellenreuther / Zastrow (1995) and Bergmann (1999) the definition of logic controls is somewhat more precise compared to DIN 19226, in that a distinction is made between logic controls with and without storage behavior.

Zander developed a new way of looking at the operational sequences of sequence controls, which was developed on the basis of a comprehensive structure and behavior analysis of control routes. For the processes in sequential control systems, the term “event-discrete process” is introduced to clarify the previously used term “discontinuous process”. It is assumed that the control variables in sequence controls are predominantly analog variables, e.g. B. Pressures, temperatures, levels, distances, angles, speeds. An essential feature of this approach is that while a discrete event process is running, the binary control signals output by the control device act in the form of step functions on the analog control variables and that their functional values ​​change in the form of step responses according to the respective time behavior. So z. B. the change in the level when filling a container on an I behavior. Corresponding threshold values ​​must be specified for the control variables. If a control variable reaches a threshold value provided for it, the binary control signal that caused the change in the control variable is set to the value zero by the control device. According to the control algorithm implemented in the control device, the next control signal is output and the discrete-event process is thus continued. Reaching a threshold value for a control variable is referred to as an "event". This explains the name “Discrete Event Process”. An event is also present when an operator action is carried out or a predetermined period of time has expired in a timer. When an event occurs, a change of operation is initiated by definition in a discrete event process. For this purpose, the events are reported to the control device by so-called event signals. Event signals are binary measurement signals, binary operating signals and binary output signals from timing elements.

On this basis, sequence controls , i. H. Control of discrete event processes, defined as follows (Zander):

A sequence control is a process in which a binary control signal is generated by an event signal arriving in the control device according to the implemented control algorithm and a step function is thereby exercised on an analog control variable, so that this control variable carries out a step response and thus an operation runs until again an event signal related to it arrives, which ends the current step response and activates further step functions of the control device, etc.

Sequence controls are characterized by successive closed partial circles (feedback) and predominantly analog control variables.

Examples of sequence controls:

• Washing machine control: In a washing machine, the water supply, detergent addition, heater and electric motor for moving the drum are started and stopped by a control system by processing information about the water level, temperature and time in connection with a selected control program in such a way that clean and spun or dry laundry is created.
• Elevator control
• Media control: audio, video and light control during a show.

In contrast to sequence controls, logic controls do not primarily change the values ​​of analog control variables, but exclusively discrete-value (e.g. binary) control variables as outputs of the control path. For this purpose, binary control signals are generated in the control device by logically combining the binary input signals, which cause the control variables to be switched. There is no feedback on a switching operation carried out from the outputs of the control path to the inputs of the control device with logic controls.

On this basis, "logic controls" are defined as follows (Zander):

A logic control is a process in which, in the event of a change in the values ​​of binary operating and / or measurement signals, a change in the values ​​of binary actuating signals occurs in accordance with a control program through a logical combination, possibly including internal states, whereby one or more two-valued or multivalued control variables occurs are influenced at the exit of the control path so that they assume the value prescribed for them by the control algorithm.

The characteristics of the logic control are an open action sequence and binary or multi-valued control variables .

The inclusion of internal states can take place through the use of storage elements. Logic controls can therefore be combinatorial systems (without memory) or sequential systems (with memories).

Examples of logic controls:

• Alternating or cross-switching for switching lights or units on and off using switches at different locations (combinatorial link control).
• Switching a signal light between idle light, fast flashing light, continuous light and slow flashing light to display a fault that has occurred or has been eliminated depending on an acknowledgment that has not yet been made or has been carried out (sequential link control).

Differentiation between binary control and regulation

Binary controls and regulations differ mainly in the following respects:

• Objectives (tasks) : Controls cause certain processes in the control objects (controlled processes), controls, on the other hand, ensure process stabilization in the presence of disturbance variables.

• Information processing : In control systems, mostly logical operations are carried out on binary signals (AND, OR, NOT, counting, storage, time functions), in control systems mainly arithmetic functions are carried out between analog quantities (difference formation, multiplication, integration, differentiation). Therefore, differential equations can be used for the description and calculation of controls, while the means of binary mathematics must be used for the description and calculation of controls. Switching algebra , applied automaton theory and the theory of Petri nets come into consideration here .

• Number of inputs and outputs : Industrial controls have a large number of inputs and outputs (typically 10 to 100 and more). In control engineering, on the other hand, single-variable controls dominate; H. Control devices with a single controlled variable as an input and a single manipulated variable as an output. Multi-variable controllers, which in principle have several inputs (controlled variables) and several outputs (manipulated variables), although not as many as controls, are rarer.

Control and PLC

In the English-language specialist literature, the word "control" is used indiscriminately for both regulation and control. This term is often simply translated as “control”. Knowledge of the context is therefore required in order to be able to translate correctly.

The English equivalent for "Programmable Logic Controller (PLC)" is "Programmable Logic Controller (PLC)", which is much more precise than the German PLC because the logical connection in the controller is emphasized as an essential feature, while the storage of the program is not emphasized remains.

Advantages and disadvantages of controls compared to regulations

Advantages of controls:

• The process of action is easy to understand.
• If a fault occurs, the process can be influenced manually.
• There can be no unstable behavior and no damaging excessive amplitudes of the control variable due to incorrectly adjusted controllers.
• A special measuring device for feedback of the control variable is not required. ${\displaystyle y(t)}$

Disadvantages of controls:

• Only known measurable disturbances can be compensated by suitable measures.
• The control path must be very well known if interference compensation is to be effective in the desired manner.
• There is no feedback as to whether the reference variable was reached by the output variable . ${\displaystyle u(t)}$ ${\displaystyle y(t)}$

The advantages and disadvantages of controls are described in the article Control technology .

Conclusion

These most recent representations make up for a decade-long failure to make control technology understandable to the general public. The distinction between control and regulation in terms of objectives, specific information processing and the number of inputs and outputs becomes clearer. In particular, the impression is counteracted that the characteristic of a control in comparison to the control loop is the open chain.

The fundamental increase in knowledge was made possible by the increased use of PLC technologies as the basis for closed sequence controls and by advances in theories, methods and computer-aided tools for controlling discrete-event processes.

Types of implementation of control devices

Connection-programmed control device (VPS)

→ Main article : Link programmed control

The connection-programmed control device is also known for short (VPS).

Note: The term control is actually a process, not a device. The control device, on the other hand, is the control device, which, however, is also referred to as the controller for short, so that confusion can occur.

Device-specific versions of connection-programmed control devices are, for example:

• mechanical control: e.g. B. pin rollers of a barrel organ, cam,
• electrical control: e.g. B. Contacts and relays,
• pneumatic or hydraulic control,
• electronic control: e.g. B. Logic Gates, Programmable Logic Circuit.

Programmable Logic Controller (PLC)

Compact PLC for small controls ( Siemens : System LOGO!)

→ Main article : Programmable logic controller

The programmable logic controller (PLC) is also called a programmable logic controller for short. The plural of programmable logic controllers is abbreviated to PLCs .

The PLC is basically a microcontroller with corresponding memories for control programs and control parameters as well as associated inputs for sensor signals and outputs for actuator signals, supplemented by human-machine interfaces for operation and interfaces for industrial communication for programming and networking.

Modular PLC of the medium and high performance class ( Siemens : System Simatic S7-1500)

The PLC is the most widely used type of control today. In principle, it can also be used as a controller , since the arithmetic-logic unit (ALU) of the internal microprocessor can solve both the logical control tasks and the arithmetic regulation tasks during information processing.

The PLC therefore also forms the basis for modern control technology for automation in the national economy. Thus, because of their universal character, the PLCs have developed into a mass product that is manufactured in millions around the world. They therefore enable a mass application of automation, combined with its widespread use in all areas of the economy and in many areas of consumer goods.

PLC technology has made a significant contribution to clarifying the conceptual boundaries between control and regulation on the one hand, and to overcoming it in terms of device technology on the other. This development process has finally also affect the philosophy and methodology of design processes for controls and regulations performed. As a result, a far-reaching methodological standardization has been achieved without negating their internal specifics and without synchronizing the PC-based design tools.

Design of controls

Design process

When designing controls, the aim is to develop a formal representation of the required process sequences for an informally specified control task, which makes it possible to create a corresponding control device so that the desired discrete-event process runs in the control system using the control signals it outputs and the measurement signals received .

In the case of connection-programmed control devices, the formal representation takes place in the form of technical drawings or circuit diagrams, which specify how the components are to be interconnected to link the binary signals. In the case of programmable logic controllers, it is a matter of creating programs through which all logical links are implemented in software.

The control design can be carried out either intuitively or empirically or systematically. Systematic design is also referred to as creating a control algorithm. The means of description and methods of switching algebra, automaton theory or Petri net theory are used.

Descriptive means for control algorithms

The descriptive means of switching algebra, automaton theory and Petri net theory can be used to first roughly note the control algorithms manually when designing controls.

Truth table

E1	E2	AND A1	OR A2	EXCL OR A3
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

The assignment of binary output signals A to binary input signals X can be represented by a truth table. The values ​​of the binary signals are indicated by the digits 0 and 1.

The truth table opposite contains 2 input signals E1 and E2, and there are 4 possible input combinations for this. In the right part of the table, the function values ​​of the three most important links are shown as outputs A1 to A3: AND, OR, Exclusive-OR (non-equivalence).

Such tables with several outputs are a shortened representation of individual tables with only one output. A table with 4 inputs contains 16 different links (see Boolean function ).

Such truth tables can be used as the starting point for the control design. After a possible simplification with the rules of switching algebra or with the Karnaugh-Veitch diagram , the result can then be used directly to implement the control device.

The control design is to be examined more closely using the following example:

Task

A patient can call the nurse by pressing a call button via an illuminated display. In contrast to a doorbell, pressing the button must lead to a permanent message in order to be noticed even if the call button is no longer pressed (memory function). The illuminated display is acknowledged (reset, deleted) by the nurse with a reset button.

Solution

	Call button E1	Reset button E2	Message E3	Message A1
1	1	1	1	1
2	1	1	0	1
3	1	0	1	1
4th	1	0	0	1
5	0	1	1	0
6th	0	1	0	0
7th	0	0	1	1
8th	0	0	0	0

The problem in the example requires storage behavior so that in addition to the sensors (E1 and E2) the actuator status, i.e. H. the output signal A1 itself must be added as an input (E3). This gives the table 8 rows.

From lines 1 to 4 it can be seen that when the call button (E1 = 1) is pressed, the display always lights up (A1 = 1), so the two inputs E2 and E3 are irrelevant ((Note: In this representation, the call button must must always be pressed if the value 1 is specified, ie type of storage cannot be recognized)). Lines 5 and 6 show that the reset (A1 = 0) is independent of input E3. The memory behavior of the control is in lines 7 and 8: The indicator light retains its (old) state (A1 = E3) if both buttons have the state 0. This means that there is an internal feedback from message output A1 to input E3.

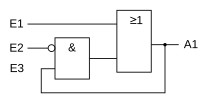
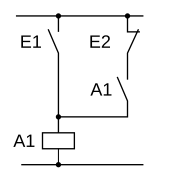
The illuminated display therefore has a memory behavior. This is a sequential link control (see definition). In the following logic plan and in the relay circuit diagram, the memory is designed as a self-holding circuit.

• Switching expression (expression of Boolean algebra or switching algebra): stands for OR, stands for AND, - stands for NOT ${\displaystyle A1=E1\lor ({\overline {E2}}\land E3)}$
  ${\displaystyle \lor }$ ${\displaystyle \land }$

Logic plan

Logic plan (function plan FBD)

• Logic plan (function plan FBD) :
  ≥1 stands for OR, & stands for AND, O stands for NOT

The logic plan is a circuit made up of electronic switching elements.

There are standardized symbols for the basic links, which are described in detail in the article Logic gates . (≥1 stands for OR, & for AND, O a circle at the input or output of the elements for NOT).

Relay wiring diagram

Relay wiring diagram

The AND link is shown as a series connection and the OR link as a parallel connection of contacts. An NC contact is used for non-linking.

The following descriptive means are particularly suitable for sequence controls of discrete-event processes:

Machine graphs

Petri networks interpreted in terms of control technology (control networks)

Technical languages ​​for PLC

For the programming of programmable logic control devices, 5 specific technical languages ​​were derived from the above description means, to which compilers are assigned, with which the source text is translated into the PLC machine language. These 5 technical languages ​​for PLCs have been gradually standardized internationally since the 1990s, to which the European standard EN 61131 and, based on this, the standard of the International Electrotechnical Commission IEC 61131-3 have made a significant contribution.

With these standardizations, essential steps were taken towards standardization in order to help PLC technology achieve its worldwide breakthrough, which has made PLC the most widely used means of automation. Today, PLCs are manufactured in millions and are used for sequence controls as well as for regulation and processing of measured values. PLCs thus form the universal core of modern automation equipment and cause their mass and widespread use.

Instruction list STL

LDN E2 A A1 O E1 = A1	LD E2 R A1 LD E1 S A1
Instruction list variant 1	Variant 2

LD stands for load, N stands for NOT, A stands for AND, O stands for OR, S stands for setting (storing), R stands for reset.

Ladder diagram LAD

Ladder diagram LAD

The ladder diagram was derived from the relay circuit diagram shown above.

Function diagram FBD

The function plan was derived from the logic plan shown above.

SFC (Sequential Function Chart)

The sequence language was derived from the Petri net interpreted in terms of control technology .

Structured text ST

In addition to the programmable logic controllers (PLC), industrial PCs (IPC) are also used, which are programmed with higher-level programming languages. This possibility also exists with modern PLCs, so that here, too, higher-level programming languages ​​are becoming more and more popular as technical languages ​​of control technology. IPCs can also provide extensive additional functions such as visualizations, logging and statistics with relatively little effort.

Running programs take time. Only hardware and software that can work synchronously with the process in the worst case scenario are suitable as control devices and are referred to as real-time capable. In a narrower sense, however, real-time means that the hardware and software of a computer are specially designed for this purpose. Controlling computers must never be overloaded because otherwise they cannot keep pace with the process flow and thus lose their real-time capability.

Process model-based control design

While the design of rules of mathematical models controlled system are included, you only mental models used in the design of binary controls in practice so far of the control path . In the 1990s, the first approaches to the model-based design of control systems were developed, which were based on the assumption that the control routes were broken down into elementary control routes. An overall model of the control path must then be formed from the resulting partial models. However, this procedure is very complex and therefore not effective in practice.

In 2005 and 2007, Zander published a new method for the design of sequence controls for discrete event processes in the trade journal “Automatisierungstechnik” , which allows the process sequences specified in the control task from a technological point of view to be implemented directly into a process model of the entire control system. The associated control algorithm can then be generated from this by simple transformations .

In a book publication, this method for process model-based design was complemented by methods for process analysis and modeling of discrete-event processes. The basis for this is a general structure and behavior analysis of control lines on the basis of the new way of looking at sequence controls (see above), from which a deeper understanding of the operational processes results.

The modeling of the discrete event processes is done by process-interpreted Petri nets. The control algorithms generated from this are displayed in the form of Petri networks interpreted in terms of control technology, which can be converted directly into a sequence language for PLC for implementation. The procedure is demonstrated using practical examples, including a. by designing an “intelligent” elevator control for ten floors.

The procedure for the process model-based control design is particularly suitable for users (process engineers, production engineers, etc.) who are used to thinking in terms of process flows. As a result, you do not have to convert the process sequences given in the control task directly into control algorithms, which is particularly difficult for newcomers. In addition, the process model initially formed for generating the control algorithm can also be used at the same time for the simulation of a designed control or additionally for an operational diagnosis .

At the same time, this innovative design strategy for controls means, for the first time, a methodical standardization of the basic procedure for design in control technology with that in control technology , without questioning the specifics of the special design processes and design tools in both areas.

See also

Wiktionary: Control technology  - explanations of meanings, word origins, synonyms, translations

Portal: Measurement, control and regulation technology  - overview of Wikipedia content on the subject of measurement, control and regulation technology

Portal: Electrical engineering  - Overview of Wikipedia content on the subject of electrical engineering

• Control unit (automotive electronics)
• cybernetics
• Circuit and system design in microelectronics
• Integrated navigation when steering vehicles
• Motion control

literature

• N. Wiener : Cybernetics. Regulation and communication in living beings and in machines. ECON-Verlag, Düsseldorf / Vienna / New York / Moscow 1968, ISBN 3-430-19652-3 .
• A. Lerner: Basics of Cybernetics. 2nd Edition. Verlag Technik, Berlin 1971.
• H. Gottschalk: Connection-programmed and programmable control devices. Verlag Technik, Berlin 1984.
• P. Neumann et al. a .: PLC standard: IEC 1131: Programming in distributed automation systems. 3. Edition. Oldenbourg-Industrieverlag, Munich / Vienna 2000, ISBN 3-8356-7005-0 .
• W. Kriesel , H. Rohr, A. Koch: History and future of measurement and automation technology. VDI-Verlag, Düsseldorf 1995, ISBN 3-18-150047-X .
• J. Lunze : automation technology. 3. Edition. R. Oldenbourg Verlag, Munich / Vienna 2012, ISBN 978-3-486-71266-7 .
• J. Müller, B.-M. Pfeiffer, R. Wieser: Rules with SIMATIC. Practical book for controls with SIMATIC S7 and SIMATIC PCS 7. 4th edition. Publicis Publication, Erlangen 2011, ISBN 978-3-89578-340-1 .
• L. Litz : Basics of automation technology. Regulation systems - control systems - hybrid systems. 2nd Edition. R. Oldenbourg Verlag, Munich / Vienna 2013, ISBN 978-3-486-70888-2 .
• M. Seitz: Programmable logic controllers. System and program design for factory and process automation, vertical integration. Specialized book publisher at Carl Hanser Verlag, Leipzig / Munich 2012.
• G. Wellenreuther, D. Zastrow: Automation with PLC - theory and practice. Programming with STEP 7 and CoDeSys, design processes, block libraries; Examples of controls, regulators, drives and safety; Communication via AS-i bus, PROFIBUS, PROFINET, Ethernet-TCP / IP, OPC, WLAN. 6th edition. Springer Vieweg, Wiesbaden 2015, ISBN 978-3-8348-2597-1 .
• H.-J. Zander : Control of discrete event processes. Novel methods for describing processes and designing control algorithms. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3 .

Web links

Commons : Control engineering  - collection of images, videos and audio files

Individual evidence

1. ↑ ^{a b} H.-J. Zander : Control of discrete event processes. Novel methods for describing processes and designing control algorithms. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3 .
2. ↑ G. Wellenreuther, D. Zastrow: Control technology with PLC. Vieweg Verlag, Wiesbaden 1995.
3. ↑ H.-J. Zander: control and regulation devices. In: H. Töpfer (Ed.): Automation technology from a manufacturer's point of view. Bürkert Steuer- und Regeltechnik, Ingelfingen 1996, ISBN 3-00-000666-4 .
4. ^ J. Lunze : automation technology. 3. Edition. R. Oldenbourg Verlag, Munich / Vienna 2012, ISBN 978-3-486-71266-7 , p. 442.
5. ↑ R. Langmann (Ed.): Pocket book of automation. Specialized book publisher in Carl Hanser Verlag, Leipzig / Munich 2004, pp. 172–176.
6. ↑ L. Litz : Basics of automation technology. Regulation systems - control systems - hybrid systems. 2nd Edition. Oldenbourg Verlag, Munich / Vienna 2013, ISBN 978-3-486-70888-2 , p. 179.
7. ↑ T. Heimbold : Introduction to automation technology. Automation systems, components, project planning and planning. Specialized book publisher at Carl Hanser Verlag, Leipzig / Munich 2015, ISBN 978-3-446-42675-7 , pp. 27-30.
8. ↑ G. Wellenreuther, D. Zastrow: Control technology with PLC. Vieweg Verlag, Wiesbaden 1995.
9. ↑ J. Bergmann: Text and exercise book automation and process control technology. An introduction for engineers and business economists. Specialized book publisher in Carl Hanser Verlag, Leipzig / Munich 1999.
10. ↑ H.-J. Zander: Control of discrete event processes. Novel methods for describing processes and designing control algorithms. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3 , pp. 38–43 and pp. 185–192.
11. ↑ H.-J. Zander: Design of sequence controls for discrete event processes on the basis of suitable control path models. In: Automation technology. Munich. Vol. 53, H. 3, 2005, pp. 140-149.
12. ↑ H.-J. Zander: A method for the process model-based design of control algorithms for parallel discrete-event processes. In: Automation technology. Munich. Vol. 55, H. 11, 2007, pp. 580-593.
13. ↑ H.-J. Zander: Control of discrete event processes. Novel methods for describing processes and designing control algorithms. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3 , pp. 177-278.