Regulator

Controllers automatically influence the physical quantities in a mostly technical process in such a way that a specified value is adhered to as well as possible, even in the event of interference.
By comparing controller within a control loop continuously the signal of the reference variable (target value) with the measured and fed back controlled variable (actual value), and determined from the difference of the two variables - the deviation (error) - A control variable which the control system affects such that the control deviation in the steady state becomes a minimum.
Because the individual control loop elements have a time behavior, the controller must increase the value of the control deviation and at the same time compensate for the time behavior of the system so that the controlled variable reaches the setpoint in the desired way - from aperiodic to dampened oscillations.
Incorrectly set controllers make the control loop too slow, lead to a large control deviation or undamped oscillations of the controlled variable and, under certain circumstances, to the destruction of the controlled system.
History of the regulator
The first water channels and their regulation are said to have been made by the Greeks since the 3rd century BC. Have been used. Historically documented regulators and regulating devices have been known since the beginning of the industrial revolution of the 18th century, which was initiated in particular by the invention of the steam engine.
The following events should be mentioned in relation to the technical design and the associated mathematical tools of the controller:
- 1788 James Watt : Centrifugal regulator for regulating the speed of steam engines.
- 1868 James Clerk Maxwell : Theoretical analysis of the centrifugal governor.
- 1922 Nicolas Minorsky : PID controller.
- 1935 electric amplifier.
- 1942 Ziegler / Nichols: Setting rules for P-, PI-; PD, PID controller.
- 1945 Bode: Frequency response analysis
- 1960 Rudolf Kalman : Kalman filter , state space , state controller and state observer.
- 1965 Lotfi Zadeh : Fuzzy set theory as the basis for later fuzzy controllers .
- 1974 Günther Schmidt : Universal controller on a microprocessor basis (digital controller), with H. Birk.
A more detailed description of the history of control engineering is contained in the article Control engineering.
Basics of the controller
Classification of controllers
In general, the controllers are differentiated according to continuous and discontinuous behavior. The “standard controllers” with P , PI , PD and PID behavior are among the best-known continuous controllers . Furthermore, there are various special types of continuous controllers with adapted behavior in order to be able to control difficult controlled systems. This includes, for example, controlled systems with dead times , with non-linear behavior, with drift of the system parameters and known and unknown disturbance variables .
With discontinuous controllers , the output variable is stepped. This includes the two- point controllers , multi-point controllers and fuzzy controllers . Optimally adapted discontinuous controllers can achieve a better dynamic behavior of the controlled variable than the standard controllers.
For more complex control systems with non-linear controlled systems or several linked controlled variables and manipulated variables, specially adapted controllers - mostly digital controllers - are required. Meshed regulations, multi-variable regulations , regulations in the state space , model-based regulations, etc. are used here.
Continuous controllers with analog or digital behavior can be used for linear controlled systems. Digital controllers have the advantage of universal adaptation to a wide variety of control tasks, but they slow down the control process through the sampling time of the controlled variable and computing time when used with fast controlled systems.
Many unstable controlled systems, which can arise, for example, from positive feedback effects ( positive feedback ), can also be controlled with classic linear controllers.
The draft of the controller is shown in the article " Control loop ". See also articles " Control system " and " Control technology ".
Description functions of the standard controllers
The transfer function is the most common mathematical description of the behavior of linear control loop elements and thus the description of the controller. It arises from the Laplace transformation of the system-describing linear ordinary differential equation and is a mathematical description of the input and output behavior of a linear, time-invariant transmission system in the frequency domain (s-domain) with the complex variable .
The independent variable is a symbol for a completed Laplace transformation of a differential quotient. The variable s - with an exponent for the degree of the derivative - in various types of representation of the transfer function can be treated algebraically as desired, but does not contain a numerical value.
By determining the zeros, the transfer function of the polynomial representation in the numerator and denominator can be split into elementary products, which are referred to as linear factors. Depending on the size of the numerical values of a transfer function in polynomial representation, the zeros of the polynomial decomposition can appear as zero, as a real number or as a conjugate complex number.
The frequency response G (jω) [formerly also F (jω)] describes the behavior of a linear time-invariant transmission system for sinusoidal input and output signals.
In contrast to the frequency response G (jω), the transfer function G (s) is not a measurable variable. Both description functions and their application are different, but the transfer function can be converted at any time with the same coefficients into the frequency response and vice versa the frequency response into the transfer function by setting the real part of the complex variable s to zero.
The application of the transfer function as a fractional-rational function is algebraic and therefore a great simplification of the mathematical effort required to assess and calculate linear transfer systems. If the transfer functions of the controlled system are known, the controller can compensate for parts of the system with the same time constants. This means that linear factors with zero points of the controller compensate linear factors with pole points of the system in order to reduce the order of the open control loop. This is understandable both algebraically and by looking at it in the Bode diagram . The design of the control loop is simplified in this way.
The following 2 forms of representation of the transfer function are common in the product representation:
- Transfer function (linear factor) in the pole-zero representation:
- Advantage: Poles and zeros can be read directly for the frequency response display.
- Transfer function (linear factor) in the time constant representation:
- The time constants are calculated from the poles and zeros. The two spellings are mathematically identical.
- Advantage: The time behavior of the system can be read directly. The gain factor of the transfer function remains constant when the time constant changes. The product representation with the time constants has the higher level of awareness.
In linear control engineering and system theory, it is a welcome fact that practically all regular (stable) transfer functions or frequency responses of control loop elements can be written or traced back to three basic forms. The linear factors have a completely different meaning, depending on whether they are in the numerator or in the denominator of a transfer function.
If the linear factors are in the numerator, they have a differentiating effect, if they are in the denominator, they have a retarding (storing) effect:
Type linear factor Meaning in the counter Meaning in the denominator
Zero "Absolute term missing"Differentiator, D-member Integrator, I-link
Zero "real number"PD1 link Delay, PT1 element
PD2 term: for 0 < D <1
with conjugate complex zerosVibration link PT2 link : for 0 < D <1
with conjugate complex poles
- Here, T is the time constant, s is the complex frequency, D degree of damping.
Transmission systems can be defined as:
- Series: .
- The superposition principle applies. The systems in the product display can be moved in any order, system outputs are not loaded by subsequent inputs.
- Parallel connection: ,
- Negative and positive feedback:
The standard linear controllers like:
- P controller ( P element ) with proportional behavior,
- I controller ( I element ) with integral behavior,
- PI controller (1 P element, 1 I element) with proportional and integral behavior,
- PD controller (PD element) with proportional and differential behavior,
- PID controller (1 I element, 2 PD elements) with proportional, integral and differential behavior
can already be described with the first two basic forms G_1 (s) and G_2 (s) of the transfer functions according to the table in a factorial representation.
Continuous linear regulator
P controller (P component)
The P controller consists exclusively of a proportional part of the gain K p . With its output signal u it is proportional to the input signal e.
The transition behavior is:
- .
The transfer function is:
The diagram shows the result of a step response . The P controller has a selected gain of K p .
Properties of the P controller:
- Reduction of the gain: Due to the lack of time behavior, the P controller reacts immediately, but its use is very limited because the gain must be greatly reduced depending on the behavior of the controlled system.
- Permanent control deviation: The control error of a step response after the controlled variable has settled as a "permanent control deviation" is 100% / Kp if there is no I element in the system.
- Controlled system as a PT1 element: In the case of a controlled system with a PT1 element (1st order delay element), the gain can theoretically be chosen to be infinitely high, because a control loop with such a controlled system cannot become unstable. This can be verified using the Nyquist stability criterion . The remaining control deviation is practically negligible. The settling of the controlled variable is aperiodic.
- Controlled system as PT2 element: With a controlled system with two PT1 elements and two dominant time constants, the limits of this controller have been reached. For example, in the case of T1 = T2 of any size and a P gain Kp = 10, this results in a permanent control deviation of 10%, a first overshoot of 35% with a degree of damping of approx. D = 0.31. For T1 ≠ T2 the amplitude of the overshoot becomes smaller and the damping better. The same attenuation always results for the same time constant ratio of any size and constant P gain.
- As the P gain increases, the control deviation becomes smaller, the overshoot larger and the damping worse.
- Integral controlled system: The P gain can theoretically be set infinitely high, with an aperiodic settling of the controlled variable. In the case of an integral controlled system with a PT1 element, there is a damped oscillating course of the controlled variable. Instability cannot arise.
I controller (I component)
An I controller (integrating controller, I element) acts by integrating the control deviation e (t) over time on the manipulated variable with the weighting through the reset time .
The integral equation is:
The transfer function is:
- Reinforcement
A constant control difference e (t) leads from an initial value of the output u1 (t) to the linear increase of the output u2 (t) up to its limitation. The reset time T N determines the gradient of the rise.
- for e (t) = constant
The reset time, for example T N = 2 s, means that at time t = 0 the output value u (t) has reached the size of the constant input value e (t) after 2 s.
The diagram shows the result of the step response of the I element. The time constant is T I = 1 s. The entry jump has the size
e (t) = 1.
Summary of the properties of the I-controller:
- Slow, accurate controller: The I controller is an accurate but slow controller due to its (theoretically) infinite gain. It leaves no permanent control deviation. Because it inserts an additional pole in the transfer function of the open control loop and, according to the Bode diagram, causes a phase angle of −90 °, only a weak gain K I or a large time constant T N can be set.
- Controlled system as a PT2 element: For a controlled system with two PT1 elements, with two dominant time constants, full instability can arise with a low gain K I. The I controller is not a suitable controller for this type of controlled system.
- Controlled system with I element: In the case of a controlled system with an I element in the control loop without additional delays, the following applies to all loop gain values K I = K I1 * K I2 instability with constant amplitude. The oscillation frequency is a function of K I (for K I > 0).
- Controlled system with dominant dead time: The I controller is the first choice for a controlled system with a dominant dead time T t or dead time without further PT1 elements. A PI controller can possibly achieve a minimal improvement. Optimal setting with negligible delay elements:
- The setting K I = 0.5 / T t leads to an overshoot of 4%, the controlled variable reaches the setpoint after T t * 3.7 s, damping D = 0.5. These settings apply to all T t values.
- Wind-up effect with large-signal behavior: If the manipulated variable u (t) is limited by the controlled system in the I-controller, a wind-up effect occurs. The integration of the controller continues to work without the manipulated variable increasing. If the control deviation e (t) becomes smaller, there is an undesired delay in the manipulated variable and thus the controlled variable when returning from . This is countered by limiting the integration to the manipulated variable limits (anti-wind-up).
- As a possible anti-wind-up measure, the I component is frozen at the last value when the input variable limit is reached (e.g. by blocking the I element). As with any limiting effect within a dynamic system, the controller behaves non-linearly. The behavior of the control loop is to be checked by numerical calculation. See also article Control loop # Influence of non-linear transmission systems on the control loop with a graphic representation of the anti-wind-up influence.
- Limit cycles: With non-linear system behavior, especially static friction, so-called limit cycles occur. In this case, the actuator cannot initially produce the target state exactly, since a certain minimum manipulated variable is not sufficient to overcome static friction. The I component that builds up ensures that the static friction is overcome, but the transition to the lower sliding friction takes place immediately. The setpoint is exceeded until the I component has reached a value below the sliding friction. The same process is then repeated with the opposite sign up to the starting position. There is a constant jerking back and forth. Limit cycles or system unrest with a constant setpoint can be avoided by keeping the manipulated variable at the existing level if the control deviation is within a tolerance range. If this is implemented by locking the controller on the input side (in software: setting e: = 0, or completely suspending the calculation of a new value) instead of keeping the output side constant, a small-signal wind-up effect of the integrator is avoided at the same time, which would otherwise occur the small but u. Long lasting deviations within the tolerance range can occur.
See also Bode diagram and locus curve of the frequency response under I-controller .
D-element (D-part)
The D element is a differentiator which is only used as a controller in connection with controllers with P and / or I behavior. It does not react to the level of the control deviation , but only to its rate of change.
Differential equation:
Transfer function:
- with T V = derivative time, T V = K D and K D = differential coefficient
“Retention time” (term according to DIN 19226 Part 2) is often incorrectly referred to colloquially as “retention time”.
The step response of the ideal D-element, as shown in the accompanying diagram, is an impact function with theoretically infinite size. The input jump is not suitable as a test signal.
A useful test signal for the D-element is the slope function:
- with the rise constant
After the Laplace transform becomes
The rise function is used in the transfer function of the D element. The output variable of the D element is thus:
and after the inverse transformation the output variable is:
with T V = K D
It can be seen from this that an increase function produces a constant output signal at the D-element. The size of the output signal depends on the product of the rise constant and the differential coefficient.
The behavior considered so far applies to the ideal differentiator. In general, a system whose transfer function has a higher order in the numerator than in the denominator is considered technically not feasible. It is not possible to use a system with excess zeros for an arbitrarily fast input signal, e.g. B. for an input jump e (t) to realize an output signal u (t) with an infinitely large amplitude.
Implementing the transfer function of an ideal controller with a D component in hardware automatically creates a delay. Therefore, the transfer function of the ideal differentiator is added a small delay (PT1-element) whose time constant T P - also called parasitic time constant - must be substantially smaller than the time constant T V .
The transfer function of the real D-element is thus:
- With
A step response of the real D-element runs asymptotically to zero with a limited size of the shock.
When realizing the real D element, PD or PID controller using analog technology using operational amplifiers, the delay with the so-called parasitic time constant T P results inevitably from limiting the counter-coupled currents , because the amplifier must remain within its operating range. (see PID controller )
Summary of the properties of the D-link:
- Differentiator: It can only differentiate, not regulate.
- D element as a component: It is preferably used as a component in PD and PID controllers.
- Compensation of I-element by D-element: The differentiator, as an ideal D-element, can theoretically completely compensate an I-element of a controlled system with the same time constants.
- Increasing function as an input variable: A linear increase in function causes a constant output magnitude proportional to the time constant T at the input V is.
- Step response of the differentiator: The step response is a shock function, which has a finite size in the real D-term and which decays to zero after an exponential function.
See also Bode diagram and locus curve of the frequency response under D-element !
PI controller
The PI controller (proportional-integral controller) consists of the portions of the P element K P and I-member having the time constant T N . It can be defined from a parallel structure or from a series structure. The term “reset time T N” comes from the parallel structure of the controller.
Integral equation of the PI controller in the parallel structure:
Transfer function of the parallel structure:
If the expression in brackets of the equation is brought to a common denominator, the product is represented in the series structure:
K PI = K P / T N is the gain of the PI controller
This product representation of the transfer function shows that two control systems as individual systems have become a series structure. This involves a PD element and an I element with the gain K PI , which are calculated from the coefficients K P and T N.
In terms of signaling, the PI controller acts compared to the I controller in such a way that, after an input jump, its effect is brought forward by the reset time T N. The steady-state accuracy is guaranteed by the I component, the control deviation becomes zero after the controlled variable has settled.
Summary of the properties of the PI controller:
- PD element without differentiation: The PD element of the PI controller created in the series structure was mathematically created without differentiation. This is why there is no parasitic delay when the controller is implemented in the parallel structure. Because of a possible wind-up effect due to the control system limitation of the manipulated variable u (t), the aim is to implement the PI controller in a parallel structure.
- Compensation of a PT1 element in the system: With the PD element, it can compensate for a PT1 element in the system and thus simplify the open control loop.
- No control deviation with a constant setpoint: The I-element means that the control deviation becomes zero in the steady state with a constant setpoint.
- Slow controller: The advantage of avoiding a steady-state control deviation gained by the I-element also has the disadvantage that an additional pole with a phase angle of −90 ° is inserted into the open control loop, which means a reduction in the loop gain K PI . Therefore the PI controller is not a fast controller.
- 2 setting parameters: The controller contains only two adjustment parameters, K PI = K P / T N and T N .
- Higher-order controlled system: It can be optimally used on a higher-order controlled system for which only the step response is known. By determining the equivalent dead time T U = delay time and the equivalent delay time constant T G = compensation time, the PD element of the controller can compensate for the time constant T G. For the I-controller setting of the remaining controlled system with equivalent dead time T U , the known setting rules apply.
- Controlled system with 2 dominant time constants: It can control a controlled system with two dominant time constants of PT1 elements if the loop gain is reduced and the longer duration of the settling of the controlled variable to the setpoint is accepted. Any desired degree of damping D can be set with K PI , oscillating from aperiodic (D = 1) to slightly damped (D towards 0).
PD controller
The PD controller (proportional-derivative controller) consists of a combination of a P element K P with a D element. It can be defined as a parallel structure or as a series structure.
The differential equation of the parallel structure is:
The transfer function of the parallel structure can be converted directly into the series structure and reads for the ideal controller:
As with the D element, a system whose transfer function has a higher order in the numerator than in the denominator is considered technically not feasible. It is not possible to use a system with excess zeros for an arbitrarily fast input signal, e.g. B. for an input jump e (t) to realize an output signal u (t) with an infinitely large amplitude.
Therefore, the transfer function of the ideal differentiator is added a small undesirable but necessary "parasitic" delay (PT1-element) whose time constant T P be substantially smaller than the time constant T must V .
The transfer function of the real PD controller is thus:
As with the D element, the step response is an impact function that is superimposed on the P component in the PD controller. The slope function is therefore the suitable test signal for the PD controller.
For the rise function, the derivative action time T V is defined as the time at which a pure P controller would have to begin before the rise function begins in order to reach the value that the D element causes.
The PD controller is a very fast controller because, unlike the PI controller, it does not add an additional pole through integration into the open control loop. Of course, the unavoidable parasitic delay with a small time constant in the control loop is also not negligible.
Summary of the properties of the PD controller:
- Compensation of a PT1 element: It can compensate a PT1 element in the controlled system and thus simplify the controlled system.
- Controlled system with 2 PT1 elements: The ideal PD controller can theoretically work with an infinitely high gain compared to the P controller in a controlled system with two PT1 elements. The remaining control deviation is practically negligible in this case. The settling of the controlled variable is aperiodic.
- Permanent control deviation: The control error of a step response after the controlled variable has settled as a permanent control deviation is 100 * K P / K P +1 [%].
PD2 term with complex conjugate zeros
PD2 elements with conjugate complex zeros can completely compensate oscillation elements (PT2 elements) with conjugate complex poles if the size of the time constants of both systems is identical. PD2 kk terms with complex conjugate zeros are obtained by subtracting the mean term of the transfer function from the transfer function of a PD2 term in polynomial representation by a specific D term.
The transfer function of a PD2 element with the same time constants is:
The transfer function of a D-element is:
PD2-term with conjugate complex zeros by subtraction with D-term:
This transfer function can be implemented using hardware or software.
If numerical values of the PD2 kk transfer function are available, the normal form with the coefficients a and b applies :
This gives the parameters of a PD2 transfer function with complex conjugate zeros:
For this numerator polynomial, analogous to the denominator polynomial (PT2 KK oscillation element), D denotes the degree of damping:
With D ≥ 1, real zeros result instead of the conjugate complex zeros.
PID controller
The PID controller (proportional-integral-derivative controller) consists of the parts of the P element, the I element and the D element. It can be defined from the parallel structure or the row structure.
The block diagram shows the series structure (product representation) and the parallel structure (sum representation) of the transfer functions of the real PID controller. The terms ideal and real PID controller indicate whether the unavoidable delay (PT1 element) required by the D component has been taken into account.
The terms P gain K P , lead time T V and reset time T N originate from the parallel controller structure. You are well known in the use of empirical controller settings in control loops with unknown control systems and low dynamic requirements.
Both forms of representation of the parallel and series structured PID controllers, which can be mathematically converted completely identically, have different advantages in their application:
- The series structure of the PID controller and the associated transfer function allow simple pole-zero compensation of the controller and the controlled system for the controller design. This form of representation is also suitable for applications in the Bode diagram.
- The parallel structure of the PID controller enables the wind-up effect to be prevented. The manipulated variable of the controller u (t) is very often limited in control loops by the controlled system. This creates the unwanted behavior of the I-link to integrate further up to its own limitation. If the manipulated variable limit disappears because the system deviation approaches zero, the value of the I element is too high and causes poor transient dynamics of the controlled variable y (t). See anti-wind-up measure in chapter I-controller of this article and article control loop , chapter: Influence of non-linear transmission systems on the control loop .
Differential equation of the ideal PID controller in parallel structure:
Transfer function of the ideal PID controller in parallel structure (sum display):
If the expression in brackets of the equation is brought to a common denominator, the result is the polynomial representation of the parallel structure of the PID controller.
Transfer function of the ideal PID controller of the parallel structure in polynomial representation:
The numerator polynomial can be solved by determining the zeros. The transfer function of the ideal PID controller in a series structure as a product representation is thus:
with the controller gain
As with the D element and PD controller, a system whose transfer function has a higher order in the numerator than in the denominator is not technically feasible. It is not possible to use a system with excess zeros for an arbitrarily fast input signal, e.g. B. for an input jump e (t) to realize an output signal u (t) with an infinitely large amplitude.
If a PID controller is implemented by connecting an operational amplifier, a resistor must limit the current in the summation point for the D component and the capacitance used with it, so that the amplifier remains within its operating range. This unintentionally but unavoidably results in an additional delay as a PT1 element, the time constant of which must be significantly smaller than the time constant T V. This delay is also called parasitic delay time constant T P designates.
The parameters of the ideal and the real PID controller can be converted as required between the parallel and in-line structures. The conversion of the real PID controller relates to the same time constant T P in both controller structures. The conversion equations are created by multiplying both transfer functions and comparing the coefficients on the Laplace operators s and s².
Recommendation of the PID controller design with reduction of the wind-up effect:
- Design of the real PID controller according to the series structure to compensate the PT1 elements of the controlled system. The parasitic time constant should be as small as possible, e.g. B. 5% of T 1; 2 of the smaller of the two time constants.
- Conversion of the real PID controller of the series structure into the parallel structure and subsequent hardware implementation of the controller. If the same parasitic time constant of the row structure is used, both controller structures have identical properties.
The mathematical description of the two structures of the ideal and real controller is shown in the table below.
PID controller Transfer function, parameters comment Ideal PID controller
series structureRecommended controller design:
pole-zero compensationIdeal PID controller
parallel structure
PID parallel structure,
common denominator.
Polynomial for factorization.Ideal PID controller
conversion from series structure
to parallel structure
Calculate controller parameters from time constants.Ideal PID controller
conversion of parallel structure
into series structureModified pq formula for calculating the time constants
if , then polynomial complex conjugate
Real PID controller
series structure with
parasitic time constantParasitic time constant: the smaller time const.
Real PID controller
parallel structure with
parasitic time constantParasitic time constant: the smaller time const.
Real PID controller
conversion from series structure
to parallel structure
Conversion applies to the
same time constant Tp in
series and parallel structure
The graphic example of the step response of a control loop with PID controller parameterization and pole-zero compensation shows (in the image enlargement) the different transfer functions of the controllers in the series and parallel structure with identical properties. The parasitic timing element of the real controller, in contrast to the ideal PID controller, causes larger overshoots in the control loop and thus poorer damping of the controlled variable y (t).
Summary of the properties of the PID controller:
- Adaptability to a controlled system: It is the most adaptable of the standard controllers, prevents a permanent control deviation in the case of a command and disturbance variable jump at a constant setpoint and can compensate for 2 delays (PT1 elements) of the controlled system and thus simplify the controlled system.
- Slow controller: The advantage of avoiding a steady-state control deviation with a constant setpoint value acquired by the I element also has the disadvantage that an additional pole with a phase angle of −90 ° is inserted into the open control loop, which means a reduction in the loop gain K PID . Therefore the PID controller (like the PI and I controller) is not a fast controller.
- Setting parameters: It contains 3 setting parameters, K PID , T1, T2 of the ideal PID controller in a series structure, or K P , T N , T V of the ideal controller in a parallel structure. The parasitic time constant T P used in the implementation of the real controller results from the hardware used. T P should preferably be very small compared to T V .
- Controlled system with 3 PT1 elements: It can control a controlled system with 3 dominant time constants of PT1 elements if the loop gain is reduced and the longer duration of the settling of the controlled variable to the setpoint is accepted. Any desired degree of damping D can be set with K PID , oscillating from aperiodic (D = 1) to slightly damped (D towards 0).
- Integral controlled system with PT1 element: It can optimally control a controlled system with an I element and a PT1 element.
- Controlled system with dominant dead time: The PID controller is unsuitable for a controlled system with a dominant dead time.
State controller
The state controller is not an independent controller, but rather it corresponds to the factor-weighted feedback of the state variables of a mathematical model of the controlled system in the state space .
The basic principle of the state controller (also called static state feedback) is the feedback of the evaluated internal system variables of a transmission system to a control loop. The individual state variables are evaluated with factors and have a subtractive effect on the reference variable w (t).
This means that parts of the state variables run through the integration chain of the computing circuit a second time according to the signal flow diagram of the normal control form. The result is a state controller with PD behavior in the state control loop.
In contrast to a standard control loop, the output variable y (t) of the state control loop is not fed back to the input of the controlled system. The reason is that the output variable y (t) is a function of the state variables. Nevertheless, an unacceptable proportional error can arise between the values of the reference variable w (t) and the controlled variable y (t), which must be eliminated by a pre-filter V.
An alternative to avoiding a control deviation is a superimposed control loop of the status control loop with a PI controller with feedback of the controlled variable y (t), which makes the prefilter V superfluous.
See detailed explanation of terms under controlled system in the state space .
Controller with status feedback
Indexing:
- Matrices = capital letters with underscore,
- Vectors = lowercase letters with underscore,
- Transposed vector representation, example:
- By default, a vector is always in column form. To get a row vector, a column vector must be transposed.
The controller state feedback (to differentiate the feedback of the state variables) relates to the state vector , which is fed back to the input variable by means of vector amplification according to the signal flow diagram of the model of the state control loop :
The linear state controller evaluates the individual state variables of the controlled system with factors and adds the resulting state products to a target / actual value comparison.
The evaluated state variables fed back with the controller run through the state space model of the route again and form new circular state variables, which results in differentiating behavior. Therefore, depending on the magnitude of order n of the differential equation of the system, the effect of the fed back state variables corresponds to that of a controller.
The following simple algebraic equations relate to the state differential equation of the variable according to the block diagram of the state space model for a single -variable controlled system, which has been expanded to include the controller state feedback.
State controller feedback equation :
The standard form of the state differential equation (also called state equation in simplified form) of the controlled system is:
If the equation of the controller feedback is inserted into the equation of state, then the equation of the state differential equation of the control loop results.
With a few exceptions, the controlled system always has more poles than zeros for control-related matters. For n> m, the output equation is simplified because the penetration (or ) equals zero. If the controlled system is a linear system , the following equations of state of the control loop result:
- Equations of the control loop state space model according to the graphical signal flow diagram shown:
equation With single-size systems State differential equation of
the control loopOutput equation of
the control loop
d = 0 for n> m
equation With multi-size systems State differential equation of
the control loopOutput equation of
the control loop
= 0 for n> m
There are essentially two design methods for state controllers. In the controller design for the pin assignment (engl pole. Placement) are for single or multivariable systems desired eigenvalues set of the control loop through the feedback controller. The quality requirements from the time domain are translated into the position of the eigenvalues. The poles can then be specified as required if the system to be controlled is fully controllable . Otherwise there are individual fixed eigenvalues that cannot be changed.
The design of a QL controller , a method for optimal control, is also based on the structure of the state feedback. Every design process must lead to a stable matrix (or ) so that the control loop is stable.
The state feedback requires knowledge of the state at all times. If the controlled system is observable , the state vector can be reconstructed from the output variables by using an observer .
See graphic diagrams for a calculation example of a state controller in the article State space representation.
Output feedback controller
Definition of terms:
- State feedback
- In a control loop, the state variables (= state vector ) evaluated in this way of the controlled system are fed back to a target / actual value comparison with the reference variable w (t) via a gain vector .
- Output return
- In a control loop with a controlled system defined in the state space, the controlled variable y (t) is fed back to a target / actual value comparison. The state variables are not used.
- A control loop with state feedback can be equipped with an output feedback through a superimposed I or PI control loop. The pre-filter V is thus superfluous and the control deviation is theoretically zero.
Conclusion:
If the effort of recording the state variables is dispensed with, only the output feedback of the controlled system is available for the design of a controller. With a controlled system as a single variable system, the output feedback for a control loop means that it is a standard control loop.
A controller with an output feedback cannot replace an optimized controller with a state feedback because the state variables react dynamically faster than the output feedback.
Multi-variable control systems with output feedback are multi-variable controls. Such multi-variable systems are also described in the matrix / vector representation.
Controller for multi-variable systems
Like the state controller, the multivariable controller is not an independent controller, but is adapted to a multivariable controlled system.
In many technical processes, several physical variables must be controlled at the same time, whereby these variables are dependent on one another. When an input variable (manipulated variable u (t)) changes, another output variable (controlled variable y (t)) or all other output variables are also influenced.
In multi-variable control systems, the input variables and output variables are linked to one another. In the control loop, the r input variables of the controlled system U1 (s) to Ur (s) are the manipulated variables of the system, which, depending on the degree of coupling, can more or less affect the different number m of controlled variables Y1 (s) to Ym (s).
Examples of simple multivariable systems:
- When generating steam, pressure and temperature are coupled,
- In air conditioning systems, temperature and humidity are coupled.
In the simple case of coupling a controlled system with 2 inputs and 2 outputs, the most common symmetrical coupling types occur in P and V canonical structures. With the P-canonical structure, an input of the path acts via a coupling element on the output of the path that is not associated with it. In the V-canonical structure, an output of the path acts via a coupling element on the input that is not associated with the path.
Depending on the type of coupled controlled systems, 3 concepts can be selected for the controller design:
- Decentralized regulation
- A separate controller is assigned to each manipulated and controlled variable pair. The interferences acting on this control loop through the coupling are compensated by the controller. This procedure is acceptable with weak coupling or with slow coupling systems compared to the main control system.
- Regulation with decoupling
- A main controller is assigned to each manipulated and controlled variable pair and a decoupling controller is assigned to the coupling between the manipulated and controlled variables. It is the task of the decoupling controller to eliminate or at least reduce the influence of the other manipulated variables on the respective controlled variable.
- Real multivariable regulation
- The multivariable controller has as many inputs as controlled variables and as many outputs as manipulated variables. The couplings between the components are taken into account in a uniform controller concept. The multivariable controller is designed using the matrix vector calculation.
Decentralized controllers for multi-variable controlled systems
In multi-variable systems, the input variables U (s) and the output variables Y (s) are weakly to strongly coupled to one another via coupled transmission systems.
In the case of controlled systems with the same number of inputs and outputs with weak coupling, decentralized controllers are used for each main system and the coupling is not taken into account. The coupled-in signal variables are regarded as disturbance variables.
For the decentralized controller, the conventional design of the controller applies with the description of the transfer function of all components, neglecting the mutual influence of coupling elements.
When using standard controllers, the simplest design strategy is the pole-zero compensation of the controller with the main control system of the open control loop. With the inverse Laplace transformation of the closed control loop, the P gain of the control loop can be optimized for an input test signal. The output variable y (t) can be displayed graphically.
It should be noted that the controller's manipulated variables are not limited by the controlled systems, otherwise this calculation and all other methods of controller dimensioning are not valid in the complex frequency range.
If the system contains non-linear elements or a system dead time, an optimal controller can be determined by numerical calculation. Either commercial computer programs are used or all non-linear components are described by logical equations, all linear components by difference equations for discrete time intervals Δt.
Multi-variable controller with decoupling
Controlled systems with strong coupling require multivariable controllers, otherwise the mutual influence of the signal variables can lead to unsatisfactory control behavior of the overall system and even loss of stability.
In the simple case of coupling a controlled system with 2 inputs and 2 outputs, the most common symmetrical coupling types occur in P and V canonical structures.
With the P-canonical structure, an input of the path acts via a coupling element (coupling element) on the output of the path that is not associated with it. In the V-canonical structure, an output of the path acts via a coupling element on the input that is not associated with the path. The coupling elements can have static, dynamic or both properties.
Modern control engineering methods are almost all based on the P-canonical structure. If the model is available as a V-canonical structure in the controlled system, it can be converted into the P-canonical structure. The controlled systems and the decoupling controllers can also be implemented in any mixed structure.
The best strategy for decoupling is to insert decoupling controllers, the effect of which is limited to decoupling the controlled system. This means that the 2 decoupled control loops can be viewed as independent single-variable control loops and the controller parameters can be changed later. The originally linked controlled system with the main controlled systems G11 (s) and G22 (s) changes to 2 independent controlled systems G S1 (s) and G S2 (s) as shown below :
The decoupling regulator is designed first. It only depends on the controlled systems and their coupling. The transfer function of the decoupling controllers for G R12 (s) and G R21 (s) is:
Decoupling controller G R12 (s) and G R21 (s)
Substitute controlled system G S1 (s)
The two open, independent, decoupled control loops have changed with regard to the controlled system due to the coupling elements. The new controlled system G S1 (s) consists of the parallel connection of the branches: G11 (s) parallel to (−1) * G R21 (s) * G12 (s)
The transfer function of the new controlled system G S1 (s) is:
If the equation for G R21 (s) is inserted into this equation , the new transfer function of the path G S1 (s) is obtained, which is completely independent in connection with the associated decoupling controller. It only depends on the transmission links of the original line with their couplings:
Substitute controlled system G S2 (s)
The two open, independent, decoupled control loops have changed with regard to the controlled system due to the coupling elements. The new controlled system G S2 (s) consists of the parallel connection of the branches: G22 (s) parallel to (−1) * G R12 (s) * G21 (s)
The transfer function of the new controlled system G S2 (s) is:
If the equation for G R12 (s) is inserted into this equation , the new transfer function of the path G S2 (s) is obtained, which is completely independent in connection with the associated decoupling controller. It only depends on the transmission links of the original line with their couplings:
The rule draft can be carried out as described in the chapter - “Decentralized controllers for multi-variable control systems”.
Multi-variable controller of any structure
The “real” multivariable controller has as many inputs r as controlled variables (as well as system deviations) and as many outputs m as manipulated variables.
The usual system description of multi-variable systems is based on the transfer function of all elements in the matrix / vector representation. As with single-variable systems, the characteristic equation of the closed control loop with its eigenvalues is also responsible for stability in multi-variable systems.
With single-loop control loops, the denominator of the transfer function of the control loop is set to zero.
The control loop is stable when the roots of the characteristic equation are in the left half of the s. (See meaning of the poles and zeros of the transfer function )
The following describes the steps to determine the transfer function matrix of the closed control loop and the associated characteristic equation:
- Establishment of the transmission matrix of the coupled controlled system,
- Establishing the matrix-vector product of the open control loop,
- Establishment of the transfer function matrix of the closed multivariable control loop,
- Representation of the characteristic equation in matrix-vector representation and scalar representation.
To make the mathematical description simple, systems with 2 coupled input and output variables are assumed. An extension to systems with several input and output variables is possible.
Establishment of the transmission matrix of the coupled controlled system
According to the illustrated block diagram of an open control loop, a controller G R (s) acts on a controlled system G (s) in a two-variable system . The coupling of the controlled system is implemented in a P-canonical structure.
The scalar equations of the controlled system can be read directly from the block diagram of the open control loop:
Establishing the matrix-vector product of the open control loop
In matrix notation, the following representation results as a transmission matrix:
In general, a controlled system with r inputs (manipulated variables) and m outputs (controlled variables) can be described by the following matrix equation:
The sizes mentioned have the following meaning:
- = Route transmission matrix,
- = Controlled variable vector,
- = Manipulated variable vector.
If the system transfer matrix and the controller transfer matrix are combined, the following matrix equation of the open control loop results:
Establishment of the transfer function matrix of the closed multivariable control loop
The transfer function matrix of the open control loop can be converted to a closed control loop with the closing condition.
According to the block diagram , the matrix equation of the controlled variable is :
The closing condition with the matrix for the r-fold control loop results in:
The transfer function matrix of the closed control loop is thus:
Representation of the characteristic equation in matrix-vector representation and scalar representation
The self-process of the closed control loop is described by:
In matrix representation this equation is:
A solution to this system of equations only exists if the determinant of ( ) vanishes. The characteristic equation of the multiple control loop is obtained:
This shows that a multi-variable system such as a single-variable system only has one characteristic equation that determines the stability behavior.
The closed multivariable control loop is I / O-stable if all poles (or, depending on the perspective, the roots) of the characteristic equation have a negative real part.
Non-linear controllers
In linear time-invariant systems ( LZI system ) without energy storage, the output variable is proportional to the input variable. In linear systems with energy stores, the output variable in the steady state is proportional to the input variable. In systems with integral behavior (I element), the output variable is proportional to the time integral of the input variable. In systems with differentiating behavior (D element), the output variable is proportional to the differential quotient of the input variable.
Mathematical operations of signals related to the output variable such as:
- Additions, subtractions, differentiations, integrations or multiplications with a constant factor of input signals result in linear behavior.
- Multiplication and division of input variables result in non-linear behavior.
In the case of non-linear transmission systems, at least one non-linear function acts in conjunction with linear systems. These non-linear functions are differentiated according to continuous and discontinuous non-linearities. Continuous non-linearities do not show any jumps in the transfer characteristic, such as B. with quadratic behavior. Discontinuous transfer characteristics such as limitations, hysteresis, response sensitivity, two-point and multi-point character do not have a continuous course.
The principle of superposition does not apply to non-linear transmission systems.
The non-linear controllers also include discontinuous controllers such as two-point, multi-point and fuzzy controllers, which are described in a separate chapter.
The calculation of non-linear systems is mostly done in the time domain. The solution of non-linear differential equations is difficult and time-consuming. This particularly relates to the group of systems with discontinuous non-linear transfer behavior or discontinuous controllers. The calculation of a control loop with switching controllers with computer-aided time-discrete processes is simpler.
Fuzzy controller (overview)
- See main article: Fuzzy Controller
Fuzzy controllers work with so-called "linguistic variables", which refer to "fuzzy quantities", such as high, medium and low. The "rule base" links the fuzzified input and output signals with logical rules such as the IF part and THEN part. With the defuzzification, the fuzzy quantity is converted back into precise control commands (e.g. valve combinations for "build up force" or "reduce force" or "hold force").
A graphical fuzzy model shows a fuzzy variable as a scaled basic set (e.g. temperature range), the mostly triangular subsets (fuzzy sets) of which are distributed on the abscissa of a coordinate system, mostly overlapping. The ordinate shows the degree of membership for each sharp value of the input variable. The maximum value of the degree of membership for each fuzzy set is μ = 1 ≡ 100%.
Application of fuzzy controller
The main application of fuzzy logic relates to fuzzy controllers for processes with several input and output variables whose mathematical models are complex or difficult to describe. These are mostly technical processes with conventional procedures that require corrective interventions by human hands (plant operators), or when the process can only be operated manually. The aim of using fuzzy logic is to automate such processes.
Application examples are the control of rail vehicles or rack conveyor systems, in which travel times, braking distances and position accuracy depend on the masses, conveying distances, rail adhesion values and schedules. In general, these processes are multi-variable systems, the reference variables of which are program-controlled and regulated. Easier uses in private households are as washing machines and dishwashers.
The basic idea of the fuzzy controller relates to the application of expert knowledge with linguistic terms, through which the fuzzy controller is optimized without a mathematical model of the process being available. The fuzzy controller has no dynamic properties.
These applications of the fuzzy controller as map controller in multi-variable systems are considered to be robust and still work relatively reliably even when the process parameters are changed.
Fuzzy controller in single-variable systems
The fuzzy controllers based on the fuzzy logic are static non-linear controllers whose input-output characteristic depends on the selected fuzzy sets and their evaluation (rule basis). The input-output characteristic can run in all quadrants of the coordinate system, especially non-linearly through the origin in the 1st and 3rd quadrants, with gaps (output variable = 0) near the origin or only positively in the 1st quadrant. As an extreme example, it can also run linearly through the choice of the position of the fuzzy sets or it can show a classic 3-point control behavior.
Fuzzy controllers have no dynamic components. As single-variable systems, they are therefore comparable in their behavior to a proportional controller (P controller), which is given any non-linear characteristic curve depending on the linguistic variables and their evaluation. Therefore, fuzzy controllers for linear single-variable controlled systems are hopelessly inferior to an optimized conventional standard controller with PI, PD or PID behavior.
Fuzzy controllers can be modified to a PID behavior by expanding the input channels with integral and differential components. They have no functional advantage over the classic PID controller, but they are capable of compensating for a non-linear function of the controlled system. With two or more signal inputs, the fuzzy controller becomes a map controller.
Adaptive controllers
- Main article: Adaptive control
Adaptive controllers are controllers that automatically adapt their parameters to the controlled system. They are thus to control time-varying control paths suitable.
Extreme value controller
- Main article: Extreme value control
Extreme value controllers are used to guide the process into an optimal state from the user's point of view and to keep it there. They are used where the measured variables compared to the manipulated variables result in a characteristic field that has an extreme.
Discontinuous regulator
With discontinuous controllers (including discontinuous controllers), the output variable u (t) is stepped. With a simple two-position controller, the output variable of the controller - the manipulated variable u (t) - can only assume 2 discrete states: If the control deviation e (t) = w (t) - y (t) is positive, the two-position controller switches on and it is zero or negative the controller switches off. If the controller has a symmetrical hysteresis, the control deviation must always be a small amount negative so that the controller switches off and an equally small amount must become positive so that the controller switches on.
Discontinuous controllers with the output signal states “On” or “Off” can also have a proportional behavior if the output variable of a classic standard controller is provided with a pulse width modulator . The controlled system acts as a low-pass filter to smooth the pulsed signals . The purpose of this process is to control large energy flows with as little loss as possible.
In the use of electrical and electronic switching elements such as relays, contactors , transistors and thyristors is desirable as low as possible switching frequency to minimize components to wear and aging. Electronic components are also subject to aging if they are operated at elevated internal temperatures. On the other hand, a low switching frequency means an increase in the ripple of the signal of the controlled variable.
Due to the electromagnetic interference of the switching processes caused by steep pulse edges, suitable interference suppression measures must be provided. (See Electromagnetic Compatibility )
As with linear transmission systems, the stability of a control loop with discontinuous controllers is of interest.
The most effective calculation method for the design, analysis and optimization of a discontinuous controller in the control loop model can be achieved numerically using commercial computer programs such as MATLAB or Simulink.
If such computer programs are not available, any number of systems and control loops with continuous, discontinuous, non-linear and linear elements can be calculated numerically for a discrete time Δt with any computer program - preferably a spreadsheet - using the combination of logical equations and difference equations . The behavior of the relevant control loop signals for a test input signal can be displayed directly in tables and graphs. (See article Control loop # Numerical calculation of dynamic transmission systems (overview) and Control loop # Control loop with discontinuous controllers )
Two-point controller
Two-point controllers can not only solve the simplest control tasks satisfactorily. You compare the controlled variable with a switching criterion that is usually subject to hysteresis and only know two states: "On" or "Off". These two-position controllers defined in this way theoretically have no time behavior.
This includes the electromechanical controllers or switching components such as B. Bimetal switches , contact thermometers , light barriers . Often these simple controllers are only suitable for a fixed setpoint.
The hysteresis behavior of the real electromechanical two-point controller is mostly caused by friction effects, mechanical play, time-dependent elastic material deformation and coupling of the system output to the input.
Electronic two-point controllers allow very good adaptation to the controlled system. Two important properties of the controller are required for this. The automatically setting switching frequency of the control loop must be increased or reduced by parameters to be set in order to achieve a desired optimum switching frequency.
For this purpose, the ideal electronic two-position controller is expanded by the following circuit measures:
- defined (hard) hysteresis through coupling of the controller output to the input (additive influence),
- Time behavior through delayed or delayed yielding feedback to the input signal (subtractive influence).
A desired behavior of the controlled variable and the switching frequency can thus be achieved with regard to the different types of controlled systems.
For special applications of the controllers and actuators, the signal processing can also take place on the basis of pneumatic or hydraulic media. The reasons for this are: explosive materials in the vicinity, high electromagnetic interference radiation, no electrical energy available, pneumatic or hydraulic energy devices are already available.
Correctly adapted two-position controllers to a controlled system can offer better dynamic properties for the controlled variable y (t) than the use of a continuous standard controller.
Applications of the two-position controller
- Controlled systems with steady-state behavior
- In principle, only controlled systems without I behavior can be used whose output variable in the steady state aims at a steady state. If the two-position controller has a positive and negative output (alternatively an active 2nd output), I-controlled systems and unstable PT1 elements can theoretically also be controlled. In practice, three-point controllers are used for motorized actuators, which have a characteristic with a "dead zone" and thus enable a switching-free idle state.
- Actuators of the controller
- The interface “output of the controller” and “input of the controlled system” is usually defined by a given controlled system. For the use of the two-point controller, only control system inputs with two-point behavior are possible. These are, for example, contactors, valves, magnets and other electrical systems.
- Small electrical loads can be controlled with relays, bimetal switches and transistors. Contactors, power transistors and thyristors are used to control the high electrical power of the actuator.
- Accuracy requirements
- Simple control loops with low accuracy requirements, in which a certain ripple ( oscillation ) around the value of the controlled variable is accepted, can be operated with electromechanical controllers. This is particularly true for controlled systems with large time constants.
- In the case of high accuracy requirements for the controlled variable, adapted electronic two-position controllers are required. This applies to fast controlled systems, the desired quasi-steady behavior of the controlled variable and good interference suppression.
Two-point controller with hysteresis
For the calculation or the simulation of a switching control loop, the behavior of the two-position controller must be clearly defined. The ideal two-position controller compares an input signal e (t)> 0 and e (t) <0 and delivers an output signal u (t) = U MAX or u (t) = u (0). In the case of a first-order controlled system, the ideal two-position controller would result in a very high switching frequency that would be determined by the randomly selected switching components and the controlled system. Therefore, a comfortable real switching regulator is assigned a hysteresis that is as adjustable as possible.
The most important component of this ideal two-point controller is the comparator , which compares 2 voltages. The hysteresis behavior is achieved through positive feedback (positive feedback) of an adjustable small portion of the output variable. A symmetrical hysteresis for the input signal e (t)> zero and e (t) <zero arises when the output variable of the comparator can assume positive and negative values. A final stage then takes care of the relationships:
According to the signal flow diagram, the size of the hysteresis relates to the output signal of the ideal two-position controller u1 (t) = ± U1 MAX , which is positively fed back to the controller input via the coupling factor K H. The control deviation e (t) as the input variable of the controller must exceed or fall below this proportion so that the two-position controller reacts.
The symmetrical range of the hysteresis is:
The coupling factor K H can be determined empirically when designing the controller. The symmetrical hysteresis influence U H can also be defined in [%] of the controller output u1 (t) = U1 MAX :
The coupling factor K H for U H [%] is:
Switching frequency in the control loop
The switching frequency of a control loop with a real two-position controller is determined by:
- the size of the time constants of the controlled system,
- the order of the differential equation or the transfer function of the controlled system,
- the size of the controller hysteresis,
- a possibly existing dead time of the controlled system,
- a positive feedback via a time-delaying element at the controller output,
- to a lesser extent by the size of the setpoint.
The switching frequency f SWITCH results from the size of the switch-on time t ON and the switch-off time t OFF in the control loop and thus determines the period duration.
The optimum switching frequency is reached when a further increase in the frequency only results in higher switching losses without improving the control deviation of the controlled variable, or when the switching superimpositions of the controlled variable are below the targeted accuracy class .
The influence of the hysteresis acts as a delay in the time-dependent control deviation e (t). The control deviation must overcome the size of the hysteresis in the positive and negative range until the controller reacts. The size of the hysteresis detunes the control deviation and thus the control variable. In many cases, a hysteresis of 0.1% to 1% of the manipulated variable is sufficient.
In the control loop with a real two-position controller with hysteresis, the switching frequency decreases with increasing hysteresis. A first-order controlled system results in a very high switching frequency, which is reduced by setting a larger hysteresis.
For a PT1 controlled system with a two-point controller with hysteresis, the course of the controlled variable y (t) can be graphically constructed as a step response. These are excerpts of the exponential rise and fall of the course of the switched PT1 element according to the time constants.
A higher-order controlled system can be viewed as a system with an equivalent dead time and leads to a low switching frequency. With additional feedback measures for the manipulated variable u (t), the switching frequency can be increased and a satisfactory control property can be achieved.
A real system dead time of more than 10% of the dominant time constant of the controlled system leads to a low switching frequency and thus to a large ripple of the signal of the controlled variable with approximately 10%. Additional feedback measures for the manipulated variable only result in an improvement with a delayed feedback. The greater the dominant time constant of the controlled system, the less critical the setting of the controller parameters. Depending on the demands on the accuracy of the controlled variable, the switching controller is more suitable in dynamic terms than a continuous standard controller for controlled systems with dead time.
Mathematical treatment of the two-position controller in the control loop
For the calculation of the control loop, standardized quantities are often introduced. If, for example, it is a question of temperature control in which the electrical energy is supplied via a contactor or power electronics, the setpoint w (t), the manipulated variable u (t) and the controlled variable y (t) can be expressed in the temperature dimension become. The step response of the manipulated variable u (t) for the value U MAX is only established after a theoretically infinite time on the controlled system.
To normalize the system variables, the maximum values of the reference variable w (t) and the controlled variable y (t) of the control loop can be represented as 100% or 1. The maximum manipulated variable U MAX must be greater than the maximum controlled variable.
The manipulated variable u1 (t) = ± U1 MAX can have any ratio to ± U MAX and is mostly determined by the electronic components used. The size of the hysteresis U H is dependent on U1 ± MAX and the coupling factor U K .
It should be noted that the heating-up time constants of the controlled system do not have to be identical to the cooling-down time constants.
The only sensible and relatively simple calculation method for a control loop with two-point and multi-point controllers is the use of commercial computer programs or the numerical treatment with the discretized time Δt on the basis of logical equations combined with the difference equations of linear systems. The behavior over time of all control loop variables is displayed directly in a table and graph.
The numerical description of the two-position controller with hysteresis consists of one simple linear and two non-linear equations. The logical description can be done with IF-, THEN-; OTHER instruction of the spreadsheet according to the signal flow diagram shown.
This controller has no time behavior, but it causes a phase shift at its output to a time-dependent input signal.
The following 3 equations to be solved numerically are specified in the order and are solved by recursion .
Linear numerical equation of the feedback for the hysteresis behavior:
(Note: is not yet known according to the order of the equations)
Nonlinear equation of the comparator:
Nonlinear equation of the manipulated variable:
The indexes with n mean: n = (0; 1; 2; 3; ...) = recursion sequence, n-1 = result one sequence behind.
To calculate a control loop, all systems of the system chain are calculated one after the other with the discrete time Δt for a recursion sequence of the same number n . n * Δt is the current time of the sequence n.
The recursion sequence for any number of n for a control loop is:
- Control deviation E (n) = W (n) - Y (n-1),
- Controller: equations of the two-position controller,
- Controlled system with linear elements: difference equations
In the article control loop with the chapter discontinuous controllers , the design with discontinuous controllers is dealt with.
Two-point controller with time-dependent feedback
The simplest bimetal controllers, which in heating systems mostly only react to a fixed temperature switching point, have been in use for a long time. In order to avoid overshoots of the controlled variable in the event of a setpoint jump and to increase the switching frequency, the active switch-on process of the switching regulator simultaneously causes the bimetal regulator to switch off prematurely through a small heating source. This behavior is called "thermal feedback".
Electronic controllers with a time-dependent feedback of the output signal allow any adaptation of the controller to the controlled system. They all have a subtracting effect on the control deviation and thus increase the switching frequency. If the influence is greater, the associated detuning of the control deviation and thus the deviation of the controlled variable from the setpoint has a disadvantage.
A much better property of the feedback results when the detuning of the control deviation only acts temporarily and then decreases exponentially .
The dynamics of the control loop are improved by the following known feedback measures of the two-position controller:
- Two-point controller with yielding feedback
- The manipulated variable of the controller acts on a PT1 element, the output signal of which subtractively influences the control deviation. A factor K R, for example in the range of 10% Umax, determines the influence of the feedback. Since the feedback constantly detunes the signal of the control deviation in the form of a sawtooth-shaped voltage with a DC voltage component, depending on the switching frequency, this type is not recommended for precise controls.
- As the time constant of the feedback increases, the switching frequency of the control loop becomes lower. As the gain increases with the factor K R , the switching frequency increases, the control deviation increases and the overshoot behavior of the controlled variable decreases.
- Two-position controllers with yielding feedback roughly correspond to the behavior of a PD controller. Overshoots after a setpoint jump are reduced. There is a constant deviation in the steady state.
- The transfer function of the feedback with a PT1 element is:
- The mathematical description of the two-position controller with hysteresis and the yielding feedback consists of 2 simple linear and 2 non-linear equations. The logical description can be done with IF-, THEN-; OTHER instruction of the spreadsheet according to the signal flow diagram shown.
- The numerical equation of the feedback for the hysteresis effect still applies:
- The hysteresis product is added and the yielding feedback u R (t) is subtracted from.
- The associated numerical equation is:
- Logical equation of the two-position controller:
- Logical equation of the manipulated variable:
- Difference equation of the PT1 element of the feedback:
- Two-position controller with delayed-yielding feedback
- Variant: 2 PT1 elements connected in parallel in differential connection
- If the yielding feedback is expanded by a parallel branch with another PT1 element with a larger time constant, which additively influences the control deviation, then the step response of this feedback runs to the value zero after a sufficiently long time.
- In the steady state of any switching frequency in the control loop, the DC voltage components of the two returned sawtooth-shaped signals of the PT1 elements are subtracted. The relatively small difference between the two ripples remains active as an alternating voltage overlay around the control deviation of the zero level. The amplitudes of this ripple are given by the size of the hysteresis or by the switching frequency that occurs.
- The result of the step response ( transition function ) of this feedback in differential circuit is a single, exponentially rapidly increasing and then exponentially flatly decreasing sinusoidal impulse towards zero. The task of the pulse is to detun the system deviation and thus to switch off the manipulated variable before the controlled variable reaches the setpoint.
- As a controller design strategy, the duration of the pulse must be adapted to the maximum rise time of the controlled variable until the setpoint is reached. With a suitable design of the feedback and the hysteresis of the controller, a larger setpoint jump in the control loop leads to a premature shutdown of the actuator and a reduction in the overshoot of the controlled variable. The control deviation is almost zero in the steady state.
- Transfer function of feedback:
- for T2 R > T1 R
- The interpretation of the PID-like behavior in two-position controllers is to be understood in such a way that the D component of the controller corresponds to the premature switch-off of the controller output and the I behavior of the controller is achieved through the high switching gain, which results in hardly any relevant control deviation. The prerequisite is that the control loop is set to the optimal switching frequency.
- Two-position controller with delayed-yielding feedback
- Variant: 2 PT1 links with a D link in product form
- This is another variant of a two-position controller with a PID-like behavior. The feedback consists of 2 PT1 elements and a D element, the D element and a PT1 element having the same time constant.
- The result of a step response of this feedback after a positive input jump is a single, dampened, rising sinusoidal impulse which drops exponentially to zero.
- The effect of these two methods of delayed yielding returns is practically identical. Only the parameters need to be set differently.
- Transfer function of feedback:
Test signals to identify the two-point controller
- Step response of the two-position controller
- In contrast to the continuous controller class (with the exception of the P controller), all forms of the two-position controller, as defined in the signal flow diagram, appear to have no time response as a step response.
- If a jump signal coming from the negative to the positive range can overcome the set hysteresis of the controller, the output signal of the controller jumps to the switching state U MAX . This is independent of the size of an existing time-dependent feedback.
- The usual standardized test signal “unit step = 1” and the associated step response are therefore not a measure for identifying the behavior of the two-position controller.
- AC voltage test signal
- The two-position controller without hysteresis reacts to the amplitudes of the alternating voltage in the zero crossing with a square-wave voltage of the amplitudes Umax of the same phase position. If the controller is assigned a symmetrically acting hysteresis, it reacts to the alternating voltage if its amplitude is greater than the hysteresis in% of the output signal Umax. Depending on the frequency of the alternating voltage, a time elapses from the zero crossing to the overcoming of the hysteresis, which causes a lagging phase shift of the right-hand voltage.
- AC voltage test signal for two-position controller with feedback
- Feedbacks of the controller output signal with time-dependent elements have a subtracting effect on the input signal in order to detune the control deviation so that the controller switches off prematurely. This reduces the overshoot of the controlled variable in the control loop when the setpoint is reached and increases the switching frequency. A delayed feedback reduces the influence of the permanent detuning of the control deviation in a time-dependent manner.
- The operation of a two-position controller and the size of the hysteresis can be checked with an alternating voltage test signal.
- To determine the time behavior of a given two-position controller with feedback using a symmetrical AC voltage test signal, the mean value of the switch-on and switch-off times during a period must be calculated. For high-quality controls of the accuracy class <1%, it should be noted that the influence of the hysteresis is of the order of magnitude <1% and the (temporary) influence of the feedback is of the order of magnitude <5%. This measuring process is difficult.
- The real qualitative assessment of the behavior of an adapted two-point controller and the required parameters for an existing controlled system is easiest possible by simulating the control loop.
Three-point controller
Three-position controllers with 3 switching states have one input and 2 outputs and switch each of the two outputs to the “On” or “Off” or “Both Off” state depending on a certain positive or negative value of the input signal e (t). They allow 2 different types of energy to be switched and have a mostly symmetrical "dead zone" with an upper and lower limit value of the control deviation e (t), in which no switching activities take place around the zero point of the control deviation.
Applications are often found in motorized actuators for flow and return and in all types of integrally acting control systems.
In the case of proportional control systems with different dominant time constants (example: rapid heating up and slow cooling down), the reaction speed of the controlled variable for changes in reference variables can be improved if a cooling unit is switched on via a three-position controller instead of the two-position controller on a heating control system.
Other applications of the three-point controller with an asymmetrical dead zone are known for reducing the fluctuation range of the controlled variable by regulating a base load with an applied partial load. Example: Annealing furnace with 2 heating devices.
As with the two-position controller, the three-position controller can, in addition to the hysteresis, have a desired time response through subtractive feedback to the input of the controller with delay elements.
As with the two-position controllers, the switching frequency decreases with increasing hysteresis.
The size of the dead zone of the three-point controller can be determined and optimized empirically or by numerical simulation. It depends on the dead time and on the number and size of the time constants or integration constants of the controlled system. A further enlargement of a dead zone determined to be optimal causes larger control deviations from the setpoint in P and I controlled systems.
System sizes of the symmetrical three-point controller
- U MAX and -U MAX correspond to the maximum and minimum manipulated variable of the controller,
- U1 MAX and -U1 MAX correspond to the maximum and minimum output of the comparator. The signal u1 (t) is advantageous for the calculation and simulation of the control loop if U1 MAX and U1 MIN are assigned to the maximum and minimum manipulated variable.
- u1 (t) or u (t) is the modulated manipulated variable of the three-point controller, which can assume the amplitudes U MAX and -U MAX or zero.
- The hysteresis in% with the influence u H (t) relates in the positive range to the output variable of the comparator U MAX and in the negative range to -U MAX . According to the block diagram and the graphic with the function table, the hysteresis is effective at the end of the positive and negative range of the dead zone. If the dead zone is zero, there are two separate hysteresis ranges for positive and negative controller output variables.
- To set the hysteresis, the ratio of U MAX to U1 MAX must be taken into account. The hysteresis factor is:
- Dead zone E DEAD
- The values of E TOT and -E TOT relate to a range of the input signal e1 (t) in which the output signal e2 (t) assumes the value zero. The dimensioning of the dead zone depends on the type of controlled system.
- The manipulated variable of a three-point controller in connection with a P-controlled system always oscillates in the positive range when the dead zone has been optimized. Too large a dead zone increases the steady-state control deviation of the controlled variable.
- The higher the order of an I controlled system and the larger the dead time, the larger the dead zone must be selected so that the controlled variable also comes into the steady switching-free state within the tolerance range. The dead zone is only effective when U TOT > the portion of the hysteresis is U H (t).
- When used in a control loop, the effect of the dead zone is considerably greater than that of the hysteresis. The dead zone is adapted to the settling behavior of the controlled variable.
Numerical description of the three-point controller with hysteresis and dead zone
- Influence of the hysteresis u H : (symmetry of the comparator signals U1 MAX and -U1 MAX assumed)
- Dead zone (2 nonlinear equations and their addition):
- Comparator with hysteresis feedback
- In the specialist literature, the usual time-independent representation of the output signal u as a function of the input signal e of the three-position controller is drawn as a positive or negative signal for the active state. This form of the output signal with the amplitudes U1 MAX and -U1 MAX is advantageous for the calculation and simulation of the control loop.
- Output variable of the comparator:
- Hysteresis proportion:
- In reality, the output signal u1 (t) shown according to the signal flow diagram is followed by 2 independent switches which control the interface of the controlled system with switches U SCH1 and U SCH2 . The switched signals correspond to U1 MAX and -U1 MAX .
Multipoint controller
In the case of multi-point controllers, which also include the three-point controller, there are additional switching states. The use of the multi-point controller requires a corresponding interface in the controlled system.
Realization of regulators
Analog controller and digital controller
- Analog regulator
- Analog controllers process continuous signals, these can theoretically be resolved as finely as desired.
- They are mostly implemented with operational amplifiers and an RC circuit (resistor-capacitor circuit) related to the control task. In technical systems where electrical energy is not available or explosion protection is required, pneumatic or hydraulic controllers are also used.
- Digital controller with signal quantization
- The continuous signal quantity fed to the controller is digitized by means of an analog-digital converter . A microcontroller can e.g. B. implement the PID control algorithm. The digital output variable of the controller (interface) must be adapted to the actuator of the controlled system. Analog actuators can be controlled with a digital-to-analog converter or, increasingly, with high-frequency pulse width modulation .
- Digital controllers have the advantage of universal adaptation to a wide variety of control tasks, but they slow down the control process by digitizing the controlled variable and the required computing time for fast controlled systems. Microcontrollers available today support resolutions of 12 bits (i.e. 4096 steps) or more with sampling intervals of 1 MHz and allow the computation of a PID algorithm in less than 100 μs. They are therefore more than sufficiently fast for most technical control systems.
Compact controller
Compact controllers are mostly digital small computers with their own standardized electrical inputs and outputs for mounting on top-hat rails or as control panel installation .
Software controller in process control systems
In the case of software controllers, the computer program is implemented as a soft PLC in a sufficiently powerful process control system (PCS). The code is executed in deterministic real time . The controller does not require direct wiring to sensors and actuators, but communicates with any actuators and sensors connected to the PCS, for example via a fieldbus system such as Profibus , EtherCAT , Interbus , Foundation Fieldbus , AS-Interface . This procedure reduces the cabling effort and facilitates the local separation of process and controller.
Universal controller
Controllers are used in many areas of application. They are often built into devices, for example the two-position controller in the electric iron, or a circuit for voltage stabilization in a power supply unit. These controllers are usually specially developed for the corresponding device and do not allow any parameter changes. In process technology, e.g. B. in the chemical industry, in power plants or in the food industry, universal controllers are used with flexible adjustment of the controller parameters
- Proportional coefficient,
- Reset time and
- Retention time
so that they can be operated as a P, PI, PD or PID controller.
A universal controller has standardized input and output signals, so-called standard signals . The input signal comes from the measuring system and the output signal acts on the actuator. It is thus possible to operate devices from different manufacturers in one control loop. Live Zero or offset zero means that the standard signal has a value, for example 4 mA, if the measured value is 0. If the standard signal is 0 mA, there must be a wire break or a short circuit. In the case of electrical standard signals, current signals are preferred. With long signal lines, they are less susceptible to external interference fields. In addition, the voltage drop on the signal line has no effect on the signal.
Pneumatic regulator
Pneumatic controllers work with standardized pneumatic inputs and outputs, for example 0.2… 1 bar or 3… 15 psi. In process engineering , for example, they are used in the explosion protection area.
Regulator without auxiliary energy
Regulators without auxiliary energy , often referred to as ROH, take on all the tasks required for regulation. They integrate the measuring sensor, the controller and also the actuator into one system and take the energy to work from the medium to be controlled. Examples are the pressure regulator of a pressure reducer for gas bottles and the bimetal thermostat of an iron.
See also
literature
- M. Horn, N. Dourdoumas: Control engineering . Pearson Studies, 2006, ISBN 3-8273-7260-7 .
- O. Föllinger: Control engineering, introduction to the methods and their application. Hüthig Verlag, 1994, ISBN 3-7785-2336-8 .
- G. Schulz: Control engineering 1: linear and non-linear control, computer-aided controller design . 3. Edition. Oldenbourg, Munich 2007, ISBN 978-3-486-58317-5 .
- M. Reuter, S. Zacher: Control technology for engineers: Analysis, simulation and design of control loops . 12th edition. Vieweg + Teubner, 2008, ISBN 978-3-8348-0018-3 .
- J. Lunze : Control engineering 1 - system theory basics, analysis and design of single-loop controls. Springer-Verlag, 2006, ISBN 3-540-28326-9 .
- H. Unbehauen : Control engineering 1. Vieweg Verlag, 2007, ISBN 978-3-528-21332-9 .
- H. Lutz, W. Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Europa-Verlag, 2019, ISBN 978-3-8085-5869-0 .
- H. Töpfer , W. Kriesel : Small automation through devices without auxiliary energy. (Automation Technology, Volume 173). Verlag Technik, Berlin 1976, 2nd edition 1978 (with Ekkehard Reimann and Mertik Quedlinburg ).
- H. Töpfer, W. Kriesel: Functional units of automation technology - electrical, pneumatic, hydraulic. Verlag Technik Berlin, VDI-Verlag, Düsseldorf 1977, 5th edition 1988, ISBN 3-341-00290-1 .
- Erwin Samal, Dirk Fabian, Christian Spieker: Outline of the practical control technology . Oldenbourg Verlag, 2013, ISBN 3-486-71290-X .
Web links
- Control engineering in the robot network wiki
- Control example: toilet flushing
- Introduction to ROH technology (PDF; 274 kB)
Individual evidence
- ↑ Lutz, Wendt: Pocket book of control engineering , chapter: Control by state feedback .
- ↑ Oliver Nelles: Lecture Concept Measurement and Control Engineering II. University of Siegen. Chapter: "Description of dynamic systems in the state space" from May 4, 2010.
- ↑ Manfred Reuter, Serge Zacher: Control technology for engineers , chapter "Multi-variable control"
- ↑ Oliver Nelles: Lecture Concept Measurement and Control Engineering II. University of Siegen. Chapter: "Multi-variable regulation" from May 4, 2010.
- ↑ H. Peter Jörgl: Lecture Notes Measurement and control VT . TU Vienna, Institute for Process Automation, SS 2006, Chapter Multi-variable control.
- ↑ Reuter, Zacher: Control technology for engineers . Chapter "Two-point controller with feedback".
- ↑ Lutz, Wendt: Pocket book of control engineering, chapter "Quasi-continuous standard controller with feedback".
- ↑ Gerd Schulz: Control engineering 1 , chapter "Three-point controller with hysteresis".
- ↑ New STM32 microcontrollers for digital controllers. In: elektroniknet.de. June 5, 2019, accessed August 3, 2019 .







































![u (t) = K_ {P} \ left [e (t) + {\ frac 1 {T_ {N}}} \ int _ {0} ^ {t} {e (\ tau)} d \ tau \ right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e6c6e51b68d2b8831c3ee132212afe1944d06f)















![{\ displaystyle u (t) = K_ {para} \ left [e (t) + {\ frac {1} {T_ {N}}} \ int _ {0} ^ {t} {e (\ tau)} d \ tau + \ T_ {V} {\ frac {d} {dt}} e (t) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f811459777456d1a715be54a1408105bc47aad2b)





























































![\ underline Y (s) = \ underline G _ {{O}} (s) \ cdot [\ underline {W} (s) - \ underline Y (s)] \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/4760a8d2ca924e88ff95b659105a8fce66313cbd)



![\ [\ underline {I} + \ underline {G} _ {O} (s)] \ cdot \ underline {Y} (s) = \ underline 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/33deadd630fd46d4c9d11073e54ebb77127e093c)







![{\ displaystyle K_ {H} = {\ frac {U_ {H} [\%] \ cdot U1_ {MAX}} {100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3f1cb12bebf807d612aa8347e39d5728cde5f79)
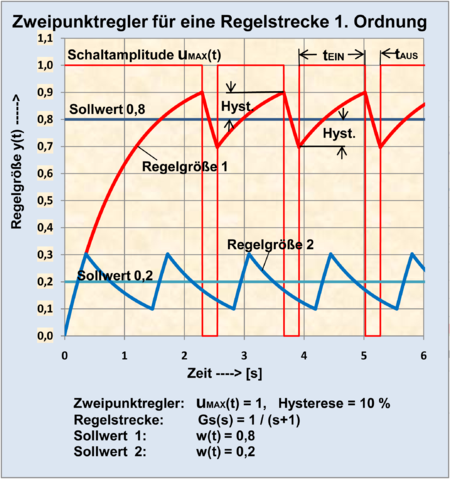



![U1 _ {{(n)}} = [IF \ \ E1 _ {{(n)}}> 0]; \ THEN \ = U1 _ {{MAX}}; \ ELSE \ = -U1 _ {{MAX}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed8d0228b58a23ad8d4854cefd32e7bb35bc8f37)
![U _ {{(n)}} = [IF \ \ U1 _ {{(n)}}> 0]; \ THEN \ = U _ {{MAX}}; \ ELSE \ = 0)](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3dabe22c72745586bd237d3901c731c74a0184)



![U _ {{(n)}} = [IF \ \ U1 _ {{(n)}}> 0]; \ THEN \ = U1 _ {{MAX}}; \ ELSE \ = 0)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d57135ff324b7587ae592e228bcb5f1c147cf1f)
![U _ {{R (n)}} = U _ {{R (n-1)}} + [K _ {{PT1}} \ cdot U _ {{R (n)}} - U _ {{R (n-1) }}] \ cdot {\ frac {\ Delta t} {T + \ Delta t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fbb017f84d227cfcdb895f5ff843576f7d91f08)


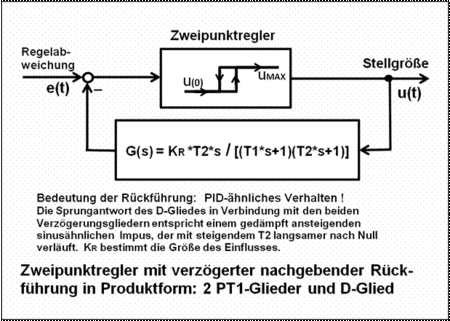

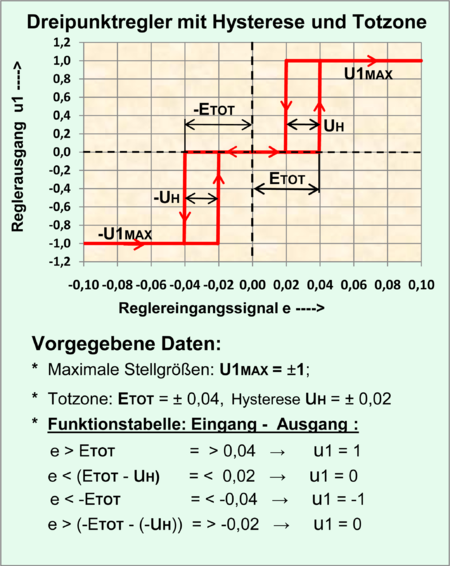
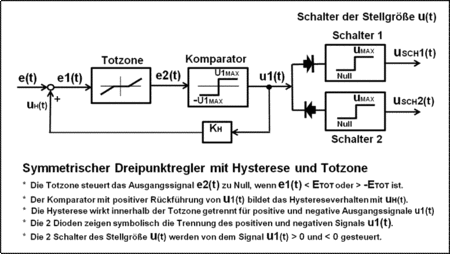
![{\ displaystyle K_ {H} (n) = {\ frac {Hysteresis [\%] * U1_ {MAX}} {U_ {MAX} * 100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6633de6a7b4f61d9f173a426f1b63529a5afbb9)





