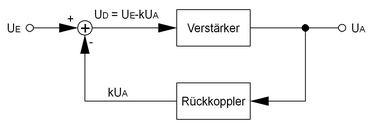
Negative feedback
The negative feedback , also counter-coupling known, is the central element of a control circuit : part of the output quantity U A is thus fed back to the input that he the input signal U E counteracts. In many systems, it is such control mechanisms that naturally restrict and stabilize growth. The principle is also used in many ways in technology.
While the negative feedback of amplifiers focuses on reducing distortion , control is more about limiting the step response and damping the transient response.
Voltage negative feedback of an operational amplifier
Operational amplifiers (OP) are designed in such a way that the technical data of an overall circuit can be defined almost exclusively by the external circuitry of the OP. For this reason, their properties can be described particularly easily and clearly.
General stability
With every operational amplifier, the gain decreases with increasing frequency and the output signal follows the changes in the input voltage with a certain delay . Because the exact data significantly influence the design of the negative feedback, they are specified in every data sheet:
- At the transit frequency f T , the gain has dropped to the value 1 (or 0 dB) (red point in the figure). At an even higher frequency, the feedback can no longer cause the OP to oscillate according to Barkhausen's stability criterion .
- With a sinusoidal input voltage, the output voltage is out of phase . The phase shift is represented by the angle β (blue bar above). If β remains in the range −180 ° <β <0 for all f <f T and the external negative feedback circuit does not add any further phase shift, the OP cannot oscillate.
The difference 180 ° - | β | is called the phase margin or phase margin φ (ger .: phase margin ), as a measure of how easily the amplifier is working. The closer this value is to 180 °, the more stable the negative feedback works. The larger β is, the lower φ is and the circuit reacts more and more "nervous" after the signal amplitude jumps, and stronger overshoots can be observed at the amplifier output . If φ becomes negative, the negative feedback has become positive feedback and the amplifier acts as an oscillator . In control engineering , it is recommended that the phase edge should be around 50 °.
The value of β can be influenced by internal or external frequency compensation of the operational amplifier.
Decrease in gain
In the adjacent circuit, the voltage divider generates the portion
the output voltage U a . Here, 0 <α ≤ 1. The feedback portion is in the operating of the signal voltage U e subtracted and the difference is displayed by the factor V amplified at the output as U a . Solving the corresponding equation, it follows
The approximation is usually accurate enough if the gain of the OpAmp exceeds 10 5 . Then the overall gain of the circuit U a / U e is practically only determined by the negative feedback. It may surprise you that the gain is deliberately decreased. With this you buy yourself enormous advantages: The bandwidth is increased, manufacturing tolerances of the OP are irrelevant and the characteristic of the OP is linearized (less distortion).
Independence from parameters
The properties of electronic components are temperature-dependent, they vary due to manufacturing and aging. If, for example, the open-loop gain V of the OP is halved, the overall gain changes only insignificantly. The gain of the operational amplifier itself is usually not linear and would actually cause signal distortion. But because operational amplifiers are always used with strong negative feedback, they are among the most linear circuits. It is sufficient if the gain in the vicinity of the zero point (differential voltage of the two inputs) is significantly greater than the overall gain of the application. The properties of analog amplifiers can only be reproduced through the systematic use of negative feedback.
Reduction of the initial resistance
If the output of an amplifier is loaded, the output voltage drops. The circuit behaves as if the cause of a non bridgeable internal resistance R a would immediately before the output. A voltage negative feedback , so to speak, informs the amplifier input about the voltage loss , which then provides so much more voltage that the nominal voltage is almost restored. Overall, the effective internal resistance is reduced to
Example: An operational amplifier has the open loop gain V = 10 5 and R a = 20 Ω. If a voltage divider with α = 0.01 is selected, the effective output resistance is only R eff = 0.02 Ω. This reduction is very desirable in most applications.
If an increase in the output resistance is necessary, this can be achieved by means of negative current feedback ( see constant current source ).
Increasing the bandwidth
In a negative feedback amplifier which is gain-bandwidth product constant and is called transit frequency f T . A change in the negative feedback affects the gain and thus the bandwidth.
- If the gain of an OP with f T = 1.3 MHz is set to V = 100 by (weak) negative feedback, it has a bandwidth of 13 kHz.
- If the gain drops to 10 with stronger negative feedback, the bandwidth increases to 130 kHz.
- In stärkstmöglicher negative feedback (α = 1), the impedance converter , the bandwidth extends to f T .
Reducing distortion
With no amplifier (without negative feedback) the output voltage is exactly proportional to the input voltage, a relationship that is represented in the form of a curved characteristic curve. The greater the curvature, the greater the harmonic content and distortion factor k of the output voltage. Both can be reduced by means of negative feedback. Since the "open loop gain" ( without negative feedback ) is always greater than 10000 in an OP , a strong negative feedback can be selected and the following applies to the distortion factor:
If, instead of the OP, a transistor or a tube with a significantly lower basic gain of only about 50 is used, the distortion factor cannot be reduced arbitrarily by negative feedback. Another peculiarity can be observed when a component with a square characteristic such as a field effect transistor is used instead of the OP :
- Without negative feedback, the quadratic distortion dominates (4%), while the cubic distortion is hardly measurable (0.04%).
- At low negative feedback the quadratic distortion, for example, 2% decreases the cubic distortion while initially to 0.1% increases .
- As the negative feedback increases, both types decrease. Since the quadratic component always predominates, the distortion factor cannot be reduced below about 1% due to the low basic gain, even with very strong negative feedback. For this reason, it is usually better to combine several stages with a strong "over-all negative feedback" than to counter-couple each amplifier stage separately.
Limits of the negative feedback
Feedback amplifiers usually show benign behavior in the case of continuous signals with small changes in amplitude. The time behavior, on the other hand, can contain surprises if a pulse (one-off, steep-edged process, part of a square-wave signal) reaches the input of a negative-feedback amplifier. The reason for this is to be found in the very broad-band spectrum of a square wave, which hardly weakening extends to extremely high frequencies. However, an OP no longer amplifies beyond its transit frequency f T and a short period of time elapses before the amplified signal appears at the output. This has nothing to do with overdrive and the resulting even more serious effects.
During this time, the negative feedback has no effect (the loop is “open”), then a “rounder” function with a slower slew rate is subtracted from the input signal, which is made worse by a capacitive load at the output.
In principle, the high-frequency spectral frequencies beyond f T cannot be compensated for by negative feedback. This leads to transient signal deviations (so-called " overshoots ", also Gibbs' phenomenon), which are greater the closer the amplifier works to its instability limit (phase edge).
The phase behavior is also influenced by the load, which is why audio amplifiers are particularly affected, as the loads operated on them ( loudspeaker box ) have a strongly frequency-dependent impedance curve.
Methods have also been developed to circumvent or compensate for certain disadvantages of negative feedback through additional circuits.
Negative feedback in problematic amplifiers
Problems always arise when the phase shift does not show such a smooth course as in the top picture. This applies to all RC- coupled amplifiers that have an upper and lower frequency limit. Even with weak negative feedback, a phase margin of almost zero can be achieved, which is sometimes desirable for raising lower frequencies (“bass booster”). Problems at the upper frequency limit always arise when using output transformers in tube amplifiers , which cause strong phase shifts in the vicinity of the natural resonance. If the transformer generates a phase shift of 180 ° at 20 kHz (phase margin φ = 0 °), the negative feedback becomes positive feedback and the circuit oscillates . There are only two antidotes:
- The gain is lowered sufficiently before 20 kHz, as required by the Barkhausen stability criterion . This drop in height is usually undesirable.
- The negative feedback will be set so weak that it is almost ineffective.
Examples
- If the predatory fish population increases in a fish basin , the individually available amount of food is reduced, which slows down, stops or even reverses further growth (example: Wator ). More complex control loops can be found in the predator-prey relationship .
- A heating system reduces the supply of additional energy when a certain temperature is reached. In this way, the further rise in temperature is slowed down.
- In electronic amplifiers with components such as transistors , electron tubes or operational amplifiers , a linearization of the transmission characteristic is achieved through negative feedback , this leads to a reduction in distortion ( distortion factor ) and a linearization of the frequency response . At the same time, the output signal is no longer so strongly determined by the amplification properties of the active component. It should be noted that at high frequencies, the inevitable phase shift turns the negative feedback into positive feedback. This can lead to undesirable oscillations if the overall gain is not reduced sufficiently by frequency compensation.
- In biology, the principle of negative feedback can be found, among other things, in the pupillary reflex to high incidence of light or the closing of the stomata when it is dry. Especially in endocrinology , the end products of a hormonal axis have an inhibitory effect on the formation of the upstream hormones: For example, the thyroid hormone triiodothyronine blocks both the formation of thyrotropin-releasing hormone (TRH) from the hypothalamus and that of the thyroid -stimulating hormone thyrotropin in the Pituitary gland (pituitary gland). Feedback is particularly important in the development of biological rhythms.
literature
- Wolfgang Bauer, Hans Herbert Wagener: Components and basic circuits of electronics. Volume 2: Basic Circuits. Carl Hanser, Munich 1981, ISBN 3-446-12319-9 .
- Gregor Häberle, Heinz Häberle, Thomas Kleiber: Expertise in radio, television and radio electronics. 3rd, revised and expanded edition. Verlag Europa-Lehrmittel, Haan-Gruiten, 1996, ISBN 3-8085-3263-7 .
- Jürgen Beetz : Feedback: How feedback determines our lives and controls nature, technology, society and the economy . Springer Spectrum, Heidelberg 2015, ISBN 978-3-662-47089-3 .
- Hendrik Wade Bode , Network Analysis an Feedback Amplifier Design , Van Nostrand, 1945, 1948, ..., 1953
Individual evidence
- ↑ Circuit practical course for operational amplifiers ( Memento of the original from June 30, 2014 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 547 kB)
- ↑ Basic internship in operation amplifier (PDF; 167 kB)
- ↑ Tietze / Schenk: Semiconductor circuit technology 2002
- ↑ another_view_of_tim pdf
- ^ The Circadian Clock . In: Albrecht U (Ed.): Protein Reviews . tape 12 . Springer-Verlag, Heidelberg, Berlin, New York, Tokyo 2010, ISBN 978-1-4419-1261-9 .
Web links
- WATOR - simulation of an ecosystem (Java applet)