Constant current source

A constant current source realizes the ideal current source within very small deviations, which feeds a constant electrical current into a circuit , regardless of the electrical voltage at its connection points and of the design of the further circuit. The current output is also known as the applied current . The limitation compared to the model of the ideal current source is the voltage that can only be emitted to a limited extent.

Principles

Equivalent circuit diagram of a real power source (with consumer)

In the case of the constant current source, the internal resistance shown in the adjacent picture of a real current source is missing; , d. H. the source has the highest possible, ideally infinite, differential resistance . The consumer flow; is ideally independent of . So that this really flows, the source builds up a suitably high electrical voltage between terminals a and b - in other words , with an ohmic consumer ${\displaystyle R_{i}=\infty }$ ${\displaystyle I_{\mathrm {K} }=I}$ ${\displaystyle R_{\mathrm {V} }}$ ${\displaystyle U_{\mathrm {kl} }}$ ${\displaystyle R_{\mathrm {V} }}$

${\displaystyle U_{\mathrm {kl} }=I\cdot R_{\mathrm {V} }\ .}$

There are also constant current sources for alternating current , for example transformer current transformers must be treated in this way. The iron-hydrogen resistor is a historical example of a constant current source suitable for all types of current, and compensation current transformers are also capable of this. Laboratory power supplies in current limiting mode or measuring transducers with a current signal ( current interface , e.g. 4–20 mA loop) are examples of direct current sources.

Direct current sources are electronic circuits that can only supply direct current - however, the output voltage can have a load-related superimposed alternating voltage. Typical implementations are presented below. The voltage that can be built up at the consumer is limited to one in these circuits , a value that remains lower than the supply voltage of the circuit. In addition to the maximum value of the current that the circuit can deliver, a maximum value of up to which it can operate as intended: ${\displaystyle U_{\mathrm {kl,max} }}$ ${\displaystyle R_{\mathrm {V} }}$

${\displaystyle 0\leq R_{\mathrm {V} }\leq U_{\mathrm {kl,max} }/I\ .}$

Example: If the circuit can build up a voltage = 12 V at the terminals with a current = 20 mA, the load may be ${\displaystyle U_{\mathrm {kl,max} }}$ ${\displaystyle I}$

${\displaystyle 0\leq R_{\mathrm {V} }\leq 600\ \Omega \ .}$

Circuits of direct current sources

With bipolar transistor

Constant current source with transistor

In the simplest case, a constant current source can be implemented by means of a negative feedback bipolar transistor . The base is kept at a constant voltage by a voltage divider consisting of the resistors and . As a result, the transistor becomes conductive and carries a certain current , which flows through the emitter resistor and causes a voltage across it according to Ohm's law . With increasing it would also increase. However, this increases the voltage of the emitter compared to the base, as a result of which the base-emitter voltage decreases. This controls the transistor and lets the current drop again immediately. If, on the other hand, it were to decrease, the voltage across the emitter resistor would be lower and thus the base-emitter voltage would be higher, whereby the collector current would increase again. This process of stabilization is also called negative feedback , which further increases the already relatively high output resistance of the transistor (see bipolar transistor characteristic fields ). ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$ ${\displaystyle I}$ ${\displaystyle R_{e}}$ ${\displaystyle U=R_{e}\cdot I}$ ${\displaystyle I}$ ${\displaystyle U}$ ${\displaystyle I}$ ${\displaystyle U}$

Since a voltage of approx. 0.7 V always drops across the base-emitter path with silicon transistors, the current is always set in such a way that it is 0.7 V lower than the applied voltage. The desired current can be set by selecting or by the voltage on . ${\displaystyle U=R_{e}\cdot I}$ ${\displaystyle R_{2}}$ ${\displaystyle R_{e}}$ ${\displaystyle R_{2}}$

The disadvantage is the strong dependency on temperature and production-related specimen variations . The circuits described below aim precisely at avoiding these weak points, which is achieved by a certain symmetry of the circuit structure (temperature-compensated constant current source).

With field effect transistor

Power source with JFET

A constant current source can be set up using a field effect transistor with (or without) a source resistor as shown in the adjacent picture. A voltage drop  that is dependent on the voltage arises , which occurs like a source resistance . The differential resistance is on the order of 1 MΩ. ${\displaystyle I_{\mathrm {D} }}$ ${\displaystyle U_{\mathrm {i} }=U_{\mathrm {DS} }+I_{\mathrm {D} }\cdot R_{\mathrm {S} }}$ ${\displaystyle r_{i}={\tfrac {\Delta U_{\text{i}}}{\Delta I_{\text{D}}}}}$

Such circuits are known as current regulating diodes and are available as finished components.

With operational amplifier

Constant current source with operational amplifier (examples)

The examples shown are voltage-current converters. An input voltage creates a current that is independent of the consumer. For understanding, the two general rules for the operational amplifier that are not overdriven are mentioned with a very good approximation :

• No voltage between the inputs,
• No power to the inputs.

- Left circuit: The current is independent of the load resistance as long as the voltage on is lower than the maximum voltage that can be supplied by the operational amplifier at its output. The voltage is at the reference potential (ground); the consumer must be potential-free . These are the same boundary conditions as above for the bipolar transistor. ${\displaystyle I=U_{e}/R_{M}\ }$
${\displaystyle R_{M}+R_{V}}$ ${\displaystyle U_{e}}$

- Middle circuit: As with the left circuit, an drops out. However, it must be potential-free here ; the consumer is interested in mass. ${\displaystyle I=U_{e}/R_{M}\ }$
${\displaystyle U_{e}}$ ${\displaystyle R_{M}}$ ${\displaystyle U_{e}}$

- Right circuit: if . Lie here , and in bulk. ${\displaystyle I=(U_{3}-U_{1})/R_{3}\ }$
${\displaystyle R_{2}:R_{1}=R_{4}:R_{3}}$ ${\displaystyle U_{1}}$ ${\displaystyle U_{3}}$ ${\displaystyle R_{V}}$

With integrated circuits

Constant current source 0 to approx. 1.8 V / 1 A with LM317

There are two-pole constant current sources as an integrated circuit (IC) for various currents in the milliampere range. There are also LED driver ICs that have one or more, often controllable, constant current sources. Such circuits work analogously or as switching regulators . In the latter case you need an external storage choke .

Constant current sources can also be implemented with integrated series regulator circuits by using their internal reference voltage to measure current on a shunt (current measuring resistor). The circuit is similar to that with a field effect transistor . The reference voltage of the LM317 is z. B. 1.25 volts - the circuit adjusts the current so that precisely this voltage drops across the shunt. The advantage compared to bipolar transistors is the low control current and the high load capacity, which is why such solutions are also suitable for higher currents in the ampere range. Disadvantages are the quite high total voltage drop, which results from the sum of the voltage on the shunt (1.25 V) and the voltage on the circuit ( drop , with the LM317 at 1 A approx. 2 V), as well as the small, however, almost constant cross current of the series regulator (up to 0.1 mA), which is added to the calculated output current.

PTAT power source

Simplified PTAT power source without decoupling

Transfer characteristics of the two circuit parts for
I _S2 = 1 · 10 ⁻¹⁵ A
n = 10
R ₃ = 100 Ω
U _T = 25.9 mV

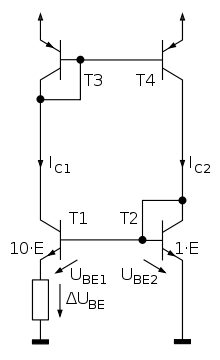
The PTAT current source supplies a current that changes proportionally to the absolute temperature (PTAT = proportional to absolute temperature ). In the adjacent circuit, T3 and T4 form an ideal current mirror and T1 and T2 form an imperfect current mirror. With the same base-emitter voltage, the emitter current of T1 is greater than that of T2, which can be achieved, for example, by connecting several transistors in parallel. The current-voltage characteristic in the picture below shows the behavior of the collector currents of T1 and T2 as a function of the base-emitter voltage U _BE2 . Due to the linear negative feedback of the exponential characteristic curve with the resistor R1, the emitter current of the transistor T2 exceeds that of T1 at a higher base-emitter voltage U _BE2 . Exact current mirroring occurs at the intersection of the characteristics. The connection with the current mirror T3 + T4 leads to a stable operating point with a constant current.

If the collector current I _C2 and the base-emitter voltage U _BE2 fall below the operating point U _cut, then the collector current I _{C1 is} greater than I _C2 . The current mirror from T3 and T4 copies the current rise from I _C1 to I _C2, whereby U _BE2 increases until the operating point is reached. Above the point of intersection, I _C2 rises faster than I _C1 and the base voltage is regulated down. The circuit regulates the two currents equally, i.e. I _C1 = I _C2 .

The current at the operating point can be calculated as follows:

${\displaystyle \Delta U_{\mathrm {BE} }+U_{\mathrm {BE1} }=U_{\mathrm {BE2} }\ \Leftrightarrow \ \Delta U_{\mathrm {BE} }=U_{\mathrm {BE2} }-U_{\mathrm {BE1} }}$

From the large-signal equation of the bipolar transistor

${\displaystyle I_{\mathrm {C} }=I_{\mathrm {S} }\cdot e^{\frac {U_{\mathrm {BE} }}{U_{\mathrm {T} }}}}$

results from the resolution according to the base-emitter voltage

${\displaystyle U_{\mathrm {BE} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C} }}{I_{\mathrm {S} }}}}$.

The different properties of the transistors T1 and T2 are characterized by the ratio of the reverse currents ${\displaystyle n}$

${\displaystyle I_{S1}=n\cdot I_{S2}}$.

The voltage across the emitter resistor is thus

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {BE2} }-U_{\mathrm {BE1} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S2} }}}-U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C1} }}{n\cdot I_{\mathrm {S2} }}}}$

Out

${\displaystyle \ln a-\ln b=\ln {\frac {a}{b}}}$

and because of the equality of the collector currents

${\displaystyle I_{\mathrm {C1} }=I_{\mathrm {C2} }}$

summarized and abbreviated the formula results:

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {T} }\cdot \ln {n}\ ;\ U_{\mathrm {T} }={\frac {k_{\mathrm {B} }\cdot T}{e_{0}}}}$

• ${\displaystyle U_{T}}$... temperature stress
• ${\displaystyle k_{\mathrm {B} }}$... Boltzmann constant
• ${\displaystyle e_{0}}$... elemental charge

Inserted into the equation for the current , this gives: ${\displaystyle I_{\mathrm {C1} }}$

${\displaystyle I_{\mathrm {C1} }=I_{\mathrm {C2} }={\frac {\Delta U_{\mathrm {BE} }}{R1}}={\frac {U_{\mathrm {T} }\cdot \ln {n}}{R1}}=T\cdot {\frac {k_{\mathrm {B} }}{e_{0}}}\cdot {\frac {\ln {n}}{R1}}}$

The current has a direct dependence on the absolute temperature. The reference current can be obtained from the current I _C1 by multiple taps on the upper current mirror .

U _BE constant current source

U _BE reference current source

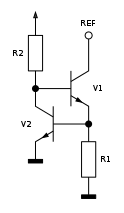
The U _BE constant current source provides the counterpart to the PTAT constant current source, as its temperature coefficient has a negative value and is to be regarded as constant over a large temperature range.

In the adjacent circuit, T1, T2 and R form an "imperfect" current mirror from I _C1 to I _C2 and T3 and T4 form an ideal current mirror from I _C2 to I _C1 .

The lower current mirror is now considered. If a current I _{C1 flows} , T2 regulates until a voltage is established at R, and thus U _BE1 , with which the entire current flows from I _C1 via T1. The base current of the transistors is negligibly low and is therefore not taken into account. Furthermore, the current I _C2 results directly from the voltage drop across the resistor .

${\displaystyle U_{\mathrm {BE1} }=U_{T}\cdot \ln {\frac {I_{\mathrm {C1} }}{I_{\mathrm {S1} }}}\Leftrightarrow I_{\mathrm {C1} }=I_{\mathrm {S1} }\cdot e^{\frac {U_{\mathrm {BE1} }}{U_{\mathrm {T} }}}}$

${\displaystyle U_{\mathrm {R} }=U_{\mathrm {BE1} }}$

${\displaystyle I_{\mathrm {C2} }={\frac {U_{\mathrm {BE1} }}{R}}}$

${\displaystyle I_{\mathrm {C2} }={\frac {U_{T}}{R}}\cdot \ln {\frac {I_{C1}}{I_{S1}}}}$

Transfer characteristic for the lower current mirror

Together with the upper current mirror, a control loop is created with a stable operating point at I _C1  = I _C2 . If the current I _{C1 is} below the operating point, the lower current mirror supplies a higher current I _C2 in relation to I _C1 . This increase leads to an increase in I _C1 via the upper current mirror until the operating point is reached. If the current I _{C1 is} above the operating point, the lower current mirror supplies a lower current I _C2 in relation to I _C1 . This reduction leads to a reduction of I _C1 via the upper current mirror until the operating point is reached.

With a given transistor parameter I _S1 and the specification of a desired current I _ref , the resistance is calculated as follows:

${\displaystyle R={\frac {U_{T}}{I_{\mathrm {ref} }}}\cdot \ln {\frac {I_{\mathrm {ref} }}{I_{S1}}}}$

The temperature dependence is proportional to the temperature coefficient of U _BE1 , assuming the change in I _C1 is negligible (I _C1  = const), then:

${\displaystyle I_{\mathrm {C2} }={\frac {U_{\mathrm {BE1} }}{R}}\Rightarrow {\frac {\mathrm {d} I_{\mathrm {C2} }}{\mathrm {d} T}}={\frac {1}{R}}\cdot {\frac {\mathrm {d} U_{\mathrm {BE1} }}{\mathrm {d} T}}}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {BE1} }}{\mathrm {d} T}}={\frac {U_{\mathrm {BE1} }-(4+M)\cdot U_{\mathrm {T} }-U_{\mathrm {G} }}{T}}}$

• M ... manufacturing parameters, value range −1.0 to −1.5
• U _G ... band gap voltage of silicon (U _G (300 K) = 1.12 V)

The reference current can be obtained from the current I _C1 by multiple taps on the upper current mirror .

Temperature compensated constant current source

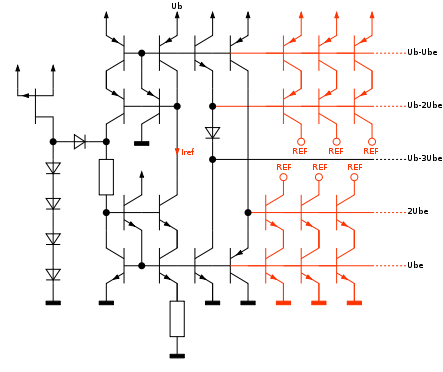
A suitable combination of PTAT and U _BE current sources creates a temperature-compensated constant current source. The band gap reference is based on a comparable concept .

Since the PTAT and the U _BE power source consist mainly of transistors and only a few resistors, both circuits are very suitable for integrated circuits . A transistor array is necessary for a discrete circuit structure because there must be a good thermal coupling between the transistors T1 and T2 as well as T3 and T4.

realization

Practical implementation of some types of reference current sources

U BE reference current source ${\displaystyle I_{\mathrm {ref} }={\tfrac {U_{\mathrm {BE,V2} }}{R_{1}}}}$ U BE reference current source with current mirror (red) and starter circuit (blue) PTAT reference current source with current mirror (red) and start-up circuit (blue)

PTAT reference current source regulated by means of two differential amplifiers (white) Temperature-independent PTAT reference power source

PTAT reference current source with cascade current mirror circuit for integrated amplifier circuits

U GS reference current source with cascade current mirror circuit for integrated MOS amplifier circuits

application

• Supply of light emitting diodes (LED) and laser diodes , see Operation and connection of LEDs
• Operating point control in operational amplifiers and other integrated circuits .
• Measurement of large capacitance values ​​(e.g. electrolytic capacitors )
• Power interfaces

Web links

• The transistor LED constant current source with one or two transistors (constant current source with opamp) . Retrieved January 8, 2011.
• The transistor LED and the FET constant current two-pole . Retrieved January 8, 2011.
• Calculate suitable resistance for constant current circuit . Frank Brall. Retrieved July 30, 2009.
• The JFET Constant Current Source - application note from Siliconix / Vishay with calculation examples (English, PDF; 79 KB) Retrieved on January 8, 2011.
• Constant current source . In: Mikrocontroller.net Wiki . Retrieved on January 8, 2010: "Schaltungssammlung"
• Precision Monolithic Temperature Sensors (PDF) National Semiconductor . Accessed January 8, 2011: "PTAT reference current source as temperature sensor"

Individual evidence

1. ↑ Erwin Böhmer: Elements of Applied Electronics. Vieweg, numerous editions
2. ↑ - ( Memento of March 3, 2014 in the Internet Archive )
3. ↑ http://www.ti.com/lit/ds/slvs044x/slvs044x.pdf data sheet of the LM317 at Texas Instruments
4. ↑ https://www.st.com/resource/en/datasheet/lm317.pdf Data sheet of the LM317 at STMicroelectronics