Band Gap Reference

As a bandgap reference ( English bandgap voltage reference ) refers to a reference voltage source whose output voltage in temperature-compensated state of the bandgap voltage of a semiconductor corresponds. The generated voltage varies depending on the semiconductor material, silicon , silicon carbide or gallium arsenide .

A special property of a band gap reference is its high precision with little circuit complexity. In addition, band gap references are temperature stable and have a low terminal voltage (<3 volts). Accordingly, the circuit has become widespread in electronics and is included, for example, in every integrated voltage regulator ( linear regulator ), as well as in many analog-digital converters .

The development of the first bandgap reference in 1971 goes back to work by Robert Widlar at National Semiconductor . Today there are further developments that have better properties and can be integrated into a CMOS process without additional work steps.

function

There are different approaches to realizing a band gap reference. Robert Allen Pease provides an overview in his article "The Design of Band-Gap Reference Circuits: Trials and Tribulations". In the following, an approach based on the Brokaw cell is analyzed step by step.

Operating point control

The picture below shows a band gap reference reduced to the control loop for stabilizing . The feedback is designed in such a way that the and the same values ​​assume. It is of decisive importance that T1 has a higher reverse saturation current , which is achieved constructively by connecting several identical transistors in parallel . ${\displaystyle I_{\mathrm {C1/C2} }}$ ${\displaystyle U_{\mathrm {R1} }}$ ${\displaystyle U_{\mathrm {R2} }}$ ${\displaystyle I_{\mathrm {S} }}$

${\displaystyle R_{1}=R_{2}}$

${\displaystyle U_{\mathrm {R1} }=R_{1}\cdot I_{\mathrm {C1} }}$

${\displaystyle U_{\mathrm {R2} }=R_{2}\cdot I_{\mathrm {C2} }}$

${\displaystyle I_{\mathrm {C} }=I_{\mathrm {S} }\cdot e^{\frac {U_{\mathrm {BE} }}{U_{\mathrm {T} }}}\cdot \left(1+{\frac {U_{\mathrm {CE} }}{U_{A}}}\right)}$ ; (Large-signal equation of the bipolar transistor )

${\displaystyle I_{\mathrm {C} }\approx I_{\mathrm {S} }\cdot e^{\frac {U_{\mathrm {BE} }}{U_{\mathrm {T} }}}}$

${\displaystyle I_{\mathrm {S1} }=n\cdot I_{\mathrm {S2} }}$

${\displaystyle I_{\mathrm {C1} }=n\cdot I_{\mathrm {S2} }\cdot e^{\frac {U_{\mathrm {BE1} }}{U_{\mathrm {T} }}}}$

${\displaystyle I_{\mathrm {C2} }=I_{\mathrm {S2} }\cdot e^{\frac {U_{\mathrm {BE2} }}{U_{\mathrm {T} }}}}$

• U _T : temperature voltage

Circuit for demonstrating the operating point control

Transfer characteristics of the two circuit parts for
I _S2 = 1 · 10 ⁻¹⁵  A
n = 10
R3 = 100 Ω
U _T = 25.9 mV
For the reference voltage, the result is:
U _Ref ≈ 702 mV

Due to the higher reverse saturation current, T1 has a higher gain factor than . However, as the emitter current increases, the resistance leads to negative feedback and ensures a flat characteristic curve . At some point T2, whose base connection is parallel to T1, catches up in the transmission characteristic. The output voltage of the differential amplifier stabilizes at the point where the two characteristics intersect. Both transistors conduct the same current there. ${\displaystyle U_{\mathrm {BE1} }}$ ${\displaystyle R_{3}}$ ${\displaystyle I_{\mathrm {E} }}$ ${\displaystyle U_{\mathrm {ref} }}$

${\displaystyle U_{\mathrm {Basis} }=\Delta U_{\mathrm {BE} }+U_{\mathrm {BE1} }=U_{\mathrm {BE2} }}$

${\displaystyle I_{\mathrm {C} }\approx I_{\mathrm {E} }}$

${\displaystyle I_{\mathrm {C1} }=I_{\mathrm {C2} }}$

The working point is calculated as follows:

${\displaystyle \Delta U_{\mathrm {BE} }+U_{\mathrm {BE1} }=U_{\mathrm {BE2} }\ \Leftrightarrow \ \Delta U_{\mathrm {BE} }=U_{\mathrm {BE2} }-U_{\mathrm {BE1} }}$

${\displaystyle U_{\mathrm {BE} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C} }}{I_{\mathrm {S} }}}\ \Leftrightarrow \ I_{\mathrm {C} }=I_{\mathrm {S} }\cdot e^{\frac {U_{\mathrm {BE} }}{U_{\mathrm {T} }}}}$

${\displaystyle U_{\mathrm {BE1} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C1} }}{n\cdot I_{\mathrm {S2} }}}\ \ ;\ \ U_{\mathrm {BE2} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S2} }}}}$

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {BE2} }-U_{\mathrm {BE1} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S2} }}}-U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C1} }}{n\cdot I_{\mathrm {S2} }}}}$

${\displaystyle \ln a-\ln b=\ln {\frac {a}{b}}\ ;\ I_{\mathrm {C1} }=I_{\mathrm {C2} }}$

Summarized and abbreviated, the formula results:

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {T} }\cdot \ln {n}\ ;\ U_{\mathrm {T} }={\frac {k_{\mathrm {B} }\cdot T}{e_{0}}}}$

• ${\displaystyle k_{\mathrm {B} }}$: Boltzmann constant
• ${\displaystyle e_{0}}$: Elementary charge

Inserted into the equation for the current , this gives: ${\displaystyle I_{\mathrm {C1} }}$

${\displaystyle I_{\mathrm {C2} }=I_{\mathrm {C1} }={\frac {\Delta U_{\mathrm {BE} }}{R3}}={\frac {U_{\mathrm {T} }\cdot \ln {n}}{R3}}}$

From this, the output voltage can finally be determined using the following equation.

${\displaystyle U_{\mathrm {Ref} }=U_{\mathrm {Basis} }=U_{\mathrm {BE2} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S2} }}}}$

Temperature coefficient

The condition

${\displaystyle \Delta U_{\mathrm {BE} }+U_{\mathrm {BE1} }=U_{\mathrm {BE2} }}$

applies to all temperature values ​​and leads directly to the condition

${\displaystyle {\frac {\mathrm {d} \Delta U_{\mathrm {BE} }}{\mathrm {d} T}}+{\frac {\mathrm {d} U_{\mathrm {BE1} }}{\mathrm {d} T}}={\frac {\mathrm {d} U_{\mathrm {BE2} }}{\mathrm {d} T}}}$.

The following applies to the voltage : ${\displaystyle U_{\mathrm {Basis} }}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}={\frac {\mathrm {d} U_{\mathrm {BE2} }}{\mathrm {d} T}}}$

To a good approximation while the true temperature drift of at constant collector current ${\displaystyle U_{\mathrm {BE} }}$ ${\displaystyle I_{\mathrm {C} }}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {BE} }}{\mathrm {d} T}}={\frac {U_{\mathrm {BE} }-(4+M)\cdot U_{\mathrm {T} }-U_{\mathrm {G} }}{T}}}$

• ${\displaystyle M}$: Manufacturing parameters, value range −1.0 to −1.5
• ${\displaystyle U_{\mathrm {G} }}$: Band gap voltage of silicon (U _G (300 K) = 1.12 V)

Temperature compensation

As shown, the output voltage (= ) still shows a clear temperature dependency, which in practice is around −1.7 mV / K. Furthermore possess and thus a positive temperature coefficient. The extension of the improved circuit (see below) consists of the resistor through which the currents and are conducted and makes use of their temperature coefficients. ${\displaystyle U_{\mathrm {ref} }}$ ${\displaystyle U_{\mathrm {BE} }}$ ${\displaystyle I_{\mathrm {C1} }}$ ${\displaystyle I_{\mathrm {C2} }}$ ${\displaystyle R_{4}}$ ${\displaystyle I_{\mathrm {C1} }}$ ${\displaystyle I_{\mathrm {C2} }}$

The temperature dependence for is shown by this formula from the section Operating point control: ${\displaystyle I_{\mathrm {C1/C2} }}$

${\displaystyle I_{\mathrm {C2} }=I_{\mathrm {C1} }={\frac {\Delta U_{\mathrm {BE} }}{R_{3}}}={\frac {U_{\mathrm {T} }\cdot \ln {n}}{R_{3}}}\ ;\ U_{\mathrm {T} }={\frac {k_{\mathrm {B} }\cdot T}{e_{0}}}}$

The further calculation shows how this dependency can be used to provide a defined temperature coefficient that compensates for the drift of the base-emitter voltage. ${\displaystyle U_{\mathrm {Temp} }}$

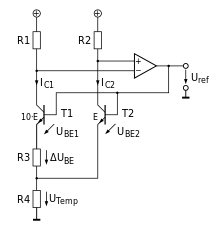
Circuit to demonstrate temperature compensation

Determination of the temperature coefficient of : ${\displaystyle U_{\mathrm {Temp} }}$

${\displaystyle U_{\mathrm {Temp} }=R_{4}\cdot \left(I_{\mathrm {C1} }+I_{\mathrm {C2} }\right)}$

${\displaystyle I_{\mathrm {C1} }={\frac {\Delta U_{\mathrm {BE} }}{R_{3}}}\ \ ;\ \ I_{\mathrm {C1} }+I_{\mathrm {C2} }=2\cdot I_{\mathrm {C1} }}$

${\displaystyle U_{\mathrm {Temp} }=R_{4}\cdot 2\cdot I_{\mathrm {C1} }=R_{4}\cdot {\frac {\Delta U_{\mathrm {BE} }}{R_{3}}}\cdot 2=2\cdot U_{\mathrm {T} }\ln n\cdot {\frac {R_{4}}{R_{3}}}}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {Temp} }}{\mathrm {d} T}}=2\cdot {\frac {\mathrm {d} U_{\mathrm {T} }}{\mathrm {d} T}}\cdot {\frac {R_{4}}{R_{3}}}\cdot \ln {n}=2\cdot {\frac {U_{\mathrm {T} }}{T}}\cdot {\frac {R_{4}}{R_{3}}}\cdot \ln {n}}$

Compensation condition:

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {Temp} }}{\mathrm {d} T}}=-{\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}={\frac {U_{\mathrm {T} }}{T}}\cdot 2\cdot {\frac {R_{4}}{R_{3}}}\cdot \ln {n}}$

${\displaystyle m={\frac {R_{4}}{R_{3}}}=-{\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}\cdot {\frac {T}{U_{\mathrm {T} }}}\cdot {\frac {1}{2\cdot \ln n}}}$

Numerical example: n = 10

${\displaystyle m={\frac {R_{4}}{R_{3}}}=-1\cdot \left(-1{,}7\,\mathrm {\frac {mV}{K}} \right)\cdot {\frac {300\,\mathrm {K} }{25{,}9\,\mathrm {mV} }}\cdot {\frac {1}{2\cdot \ln 10}}\approx 4{,}28}$

Output voltage

The output voltage increases when the temperature compensation is added and is in the range of the band gap voltage of the semiconductor used. When targeted value of U _G (0 K) = 1.205 V is the extrapolated band gap voltage at 0 K, starting from the reference temperature T . In fact, the band gap voltage of semiconductors does not show a linear behavior at low temperatures, which is why the true band gap is 1.17 V. The resulting output voltage is to be determined in a numerical example. ${\displaystyle U_{\mathrm {ref} }}$ ${\displaystyle U_{\mathrm {G} }}$

${\displaystyle U_{\mathrm {ref} }=U_{\mathrm {BE2} }+U_{\mathrm {Temp} }}$

Parameter:

I _S0 = 1 · 10 ⁻¹⁵ ; n = 10; I _S1 = n * I _S0 ; I _S2 = I _S0 ; R ₃ = 100 Ω; M = 1.5; T = 300 K

In the first step, the operating point and thus must be determined. ${\displaystyle I_{\mathrm {C1/C2} }}$

${\displaystyle I_{\mathrm {C2} }=I_{\mathrm {C1} }={\frac {\Delta U_{\mathrm {BE} }}{R3}}={\frac {U_{\mathrm {T} }\cdot \ln {n}}{R_{3}}}={\frac {25{,}9\,\mathrm {mV} \cdot \ln {10}}{100}}=0{,}596\,\mathrm {mA} }$

${\displaystyle U_{\mathrm {Basis} }=U_{\mathrm {BE2} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S2} }}}=25{,}9\,\mathrm {mV} \cdot \ln {\frac {0{,}596\,\mathrm {mA} }{1\cdot 10^{-15}}}=702\,\mathrm {mV} }$

From , and the parameters, R4 can now be calculated for the temperature compensation and the voltage U _Temp . ${\displaystyle U_{\mathrm {Basis} }}$ ${\displaystyle I_{\mathrm {C1/C2} }}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {BE} }}{\mathrm {d} T}}={\frac {U_{\mathrm {BE} }-(4+M)\cdot U_{\mathrm {T} }-U_{\mathrm {G} }+U_{\mathrm {T} }}{T}}={\frac {702\,\mathrm {mV} -(4-1{,}5)\cdot 25{,}9\,\mathrm {mV} -1120\,\mathrm {mV} }{300\,\mathrm {K} }}=-1{,}61\,\mathrm {\frac {mV}{K}} }$

${\displaystyle m={\frac {R_{4}}{R_{3}}}=-{\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}\cdot {\frac {T}{U_{\mathrm {T} }}}\cdot {\frac {1}{2\cdot \ln n}}=-1\cdot \left(-1{,}61\,\mathrm {\frac {mV}{K}} \right)\cdot {\frac {300\,\mathrm {K} }{25{,}9\,\mathrm {mV} }}\cdot {\frac {1}{2\cdot \ln 10}}\approx 4{,}05}$

${\displaystyle R_{4}=m\cdot R_{3}=4{,}05\cdot 100\,\Omega =405\,\Omega }$

${\displaystyle U_{\mathrm {Temp} }=2\cdot I_{\mathrm {C1} }\cdot R_{4}=2\cdot 0{,}596\,\mathrm {mA} \cdot 405\,\Omega =483\,\mathrm {mV} }$

${\displaystyle U_{\mathrm {ref} }=U_{\mathrm {Basis} }+U_{\mathrm {Temp} }=0{,}702\,\mathrm {V} +0{,}483\,\mathrm {V} =1{,}18\,\mathrm {V} }$

Results:

R ₄ = 478 Ω; U _base = 0.702 V; U _Temp = 0.483 V; U _ref = 1.18V

The output voltage determined in the numbers game is 1.18 V only a few percent below the expected value of 1.205 V. ${\displaystyle U_{\mathrm {ref} }}$

Discrete structure

In practice, only integrated circuits are used, but a discrete structure offers incentives for laboratory tests and electronic tinkering. This faces a fundamental problem in that transistor arrays to achieve the required reverse saturation current ratio are difficult to obtain. A way out is to reduce the resistance of . As a result, at the operating point through T2, a multiple of the current flows through T1, which has an effect similar to that of the multiple saturation blocking current and the resulting voltage current gain. The use of a double transistor is advisable in order to keep the manufacturing spread as low as possible and to achieve a good thermal coupling. ${\displaystyle R_{2}}$

The most important formulas summarized:

${\displaystyle R2={\frac {1}{n}}\cdot R1\ ;\ I_{\mathrm {C2} }=n\cdot I_{\mathrm {C1} }}$

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {BE2} }-U_{\mathrm {BE1} }=U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C2} }}{I_{\mathrm {S} }}}-U_{\mathrm {T} }\cdot \ln {\frac {I_{\mathrm {C1} }}{I_{\mathrm {S} }}}=U_{\mathrm {T} }\cdot \ln {n}}$

${\displaystyle I_{\mathrm {C1} }={\frac {\Delta U_{\mathrm {BE} }}{R3}}}$

${\displaystyle U_{\mathrm {Temp} }=R_{4}\cdot I_{\mathrm {C1} }\cdot \left(1+n\right)=R_{4}\cdot {\frac {\Delta U_{\mathrm {BE} }}{R_{3}}}\cdot \left(1+n\right)={\frac {R_{4}}{R_{3}}}\cdot U_{\mathrm {T} }\cdot \ln {n}\cdot \left(1+n\right)}$

${\displaystyle -{\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}={\frac {\mathrm {d} U_{\mathrm {Temp} }}{\mathrm {d} T}}={\frac {R4}{R3}}\cdot {\frac {U_{\mathrm {T} }}{T}}\cdot (1+n)\cdot \ln n}$

${\displaystyle m={\frac {R4}{R3}}=-{\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}\cdot {\frac {T}{U_{\mathrm {T} }}}\cdot {\frac {1}{(1+n)\cdot \ln n}}}$

${\displaystyle {\frac {\mathrm {d} U_{\mathrm {BE} }}{\mathrm {d} T}}={\frac {\mathrm {d} U_{\mathrm {Basis} }}{\mathrm {d} T}}={\frac {U_{\mathrm {BE} }-(4+M)\cdot U_{\mathrm {T} }-U_{\mathrm {G} }}{T}}}$

Temperature sensor

A variable that is proportional to the absolute temperature is called PTAT (proportional to absolute temperature) . Such a property has ΔU _BE and consequently U _Temp in the Brokaw cell. ${\displaystyle T}$

${\displaystyle \Delta U_{\mathrm {BE} }=U_{\mathrm {T} }\cdot \ln n=T\cdot {\frac {k_{\mathrm {B} }}{e_{0}}}\cdot \ln n}$

${\displaystyle U_{\mathrm {Temp} }=U_{\mathrm {T} }\cdot 2\cdot {\frac {R_{4}}{R_{3}}}\cdot \ln n=T\cdot {\frac {k_{\mathrm {B} }}{e_{0}}}\cdot 2\cdot {\frac {R_{4}}{R_{3}}}\cdot \ln n}$

This feature can be used to measure temperature and directly reflects the temperature of the chip material.

various

"Parasitic" pnp transistor in CMOS structure

The term curvature correction refers to measures to compensate for the remaining temperature dependence of the band gap reference.

The bipolar transistors required for a band gap reference are only available in CMOS technology via the complex BiCMOS . That is why the “parasitic” pnp transistors feared by the latch-up effect are used.

A bandgap reference developed in the late 1990s is based on JFETs . These are known under protected brand names such as XFET . Band gap references of this type sometimes have better properties than circuits implemented with bipolar transistors and can also be used at lower supply voltages.

literature

• Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology . 12th edition. Springer Verlag, Berlin, Heidelberg, New York 2002, ISBN 3-540-42849-6 .
• TH Lee: Tales of the Continuum: A Subsampled History of Analog Circuits . In: IEEE / SSC . 2007 ( online ).
• Patent US3617859 : Electrical Regulator Apparatus Including a Zero Temperature Coefficient Voltage Reference Circuit. Published March 23, 1970 , Inventors: Robert C. Dobkin, Robert J. Widlar. ‌
• Patent US3887863 : Solid-State Regulated Voltage Supply. Published November 28, 1973 , inventor: Adrian Paul Brokaw. ‌

Web links

Commons : Bandgap voltage reference  - collection of images, videos and audio files

• IC Provides On-Card Regulation for Logic Circuits - Rober Widlar, February 1971, National Semiconductor (PDF file)
• A High Precision Bandgap Reference Used in Power Management ICs - Gu Shurong, Wu Xiaobo, Yan Xiaolang (PDF file; 453 kB)
• Bandgap Reference Circuit - Vinay Agarwal (PDF file; 304 kB). Archived from the original on February 21, 2007 ; Retrieved September 9, 2015 . 
• Z-Diode Extension Course and the Bandgap Reference - elektronik-kompendium.de

Individual evidence

1. ↑ ^{a b} Robert Pease: The Design of Band-Gap Reference Circuits: Trials and Tribulations  ( page no longer available , search in web archives )  Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice.  
2. ↑ IC Provides On-Card Regulation for Logic Circuits ( Memento of the original from November 19, 2008 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. - Rober Widlar, February 1971, National Semiconductor (PDF file).  
3. ↑ XFET ™ References from Analog Devices . (in English)