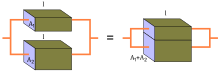
Parallel connection

The title of this article is ambiguous. Further meanings are listed under parallel connection (definition of terms ) .

The parallel connection , also called ancillary connection , is the connection of two-pole components or networks in electrical engineering in such a way that all their poles of the same name are connected together. If unlike poles are connected to one another in polarized components (e.g. batteries, diodes, electrolytic capacitors), one speaks of an anti-parallel circuit. This distinction does not apply to non-polarized passive components . The number of elements connected in parallel is arbitrary. As a counterpart to the parallel connection, there is another essential basic connection, the series connection .

Below: parallel connection of two resistors, in contrast to
above: series connection

notation

The parallel connection of components can be noted in mathematical expressions with two vertical lines between their symbols. For example to the first picture: Just as you can write for the upper part , the spelling is common for the lower part . ${\displaystyle U_{0}/I_{0}=R_{1}+R_{2}}$ ${\displaystyle U_{0}/I_{0}=R_{1}\|R_{2}}$

Properties of a parallel connection

Circuit diagrams of various parallel connections

The parallel connection of several elements has the following features:

• The same electrical voltage is applied to all elements of a parallel circuit , even if their current consumption is different. A typical example is the mains voltage supply (230 V in the household): All devices - regardless of their power consumption - are supplied with the same voltage.
• The parallel connection of several electrical consumers with an ideal voltage source is not susceptible to failure of individual consumers (in the event of failure in the sense of an interruption). If an individual element interrupts its electrical line or is removed from the line, all intact consumers are supplied unchanged. With a real voltage source, the failure increases the voltage on the intact consumers. - In the event of a failure in the sense of a short circuit, the entire circuit fails unless the line of the failed consumer is interrupted by a fuse .
• The parallel connection of relay contacts with the states "blocked" and "conductive" implements an OR function for the state "conductive" and an AND function for the state "blocked".

In process engineering, pressure and temperature differences are physical analogies to potential differences . For example, electrical equivalent circuit diagrams can be created for cooling circuits or heat transfers in order to calculate their properties according to the rules of electrical engineering.

• Several pumps working in parallel deliver a higher flow rate, but no higher pressure if the line is designed accordingly.
• The flow (analogous to the current strength) in individual elements of a heat exchanger system connected in parallel (for example a heating system) depends on their flow resistances.

Laws in parallel connections

Linear electrical networks
Ideal element
Electrical component
Series and parallel connection
Network transformations
Generator sets	Network sentences
Network analysis methods
Two-port parameters

Ohm's law applies to ohmic resistances

${\displaystyle U=R\cdot I}$,

wherein the electrical voltage , the electrical resistance and the electrical current is. This applies to constant quantities , as well as rms values and instantaneous values for quantities that change over time. ${\displaystyle U}$ ${\displaystyle R}$ ${\displaystyle I}$

The total resistance of a parallel connection decreases with every additional ohmic consumer. The total resistance is therefore always smaller than the smallest individual resistance. An exception is a parallel oscillating circuit with alternating voltage .

tension

The electrical voltage is identical for all sub-branches in terms of frequency , phase angle and amplitude . ${\displaystyle U}$

${\displaystyle U_{\mathrm {ges} }=U_{1}=U_{2}=\ldots =U_{n}}$

Amperage

With the parallel connection, the current intensity is distributed to the individual branches according to the Kirchhoff rule . The sum of the partial currents is equal to the total current. ${\displaystyle I_{\mathrm {ges} }}$

${\displaystyle I_{\mathrm {ges} }=\sum \limits _{n=1}^{N}I_{n}=I_{1}+I_{2}+\ldots +I_{N}}$

With alternating current through components with reactance (coils, capacitors), the partial currents add Pythagorean to the total current. In individual cases, the partial current strength of a component of the parallel connection can even exceed the total current strength (excessive current ).

power

The total performance is the sum of the performance of each consumer:

${\displaystyle P_{\mathrm {ges} }=\sum \limits _{n=1}^{N}P_{n}=P_{1}+P_{2}+\ldots +P_{N}=U\cdot \sum \limits _{n=1}^{N}I_{n}=U\cdot I_{\mathrm {ges} }}$

Parallel connections

Voltage sources

A parallel connection of ideal voltage sources leads to unlimited high currents between the sources.

If more current is required by the consumer than a single source can supply, so that a parallel connection of voltage sources is necessary, this is only possible to a limited extent with real sources. Details are given under voltage source # parallel connection . The parallel connection of power transformers can also be desirable, but it is only possible under special conditions, see Power transformer # Parallel connection .

In microprocessor technology, a number of voltage sources are connected in parallel on the data bus . To do this, they have to be connected to the bus via coupling modules that have a tri-state behavior. With this, each data output can not only output one of the two possible logic levels , but it can also be switched to high resistance . Addressing and clock signal only enable one data output at a time.

Power sources

When two potential-free or similarly earthed current sources are connected in parallel (term in the sense of circuit theory, i.e. no voltage sources!), A total current strength is formed equal to the sum of the partial current strengths , etc., whereby their signs must be observed according to the node rule. ${\displaystyle I_{\mathrm {ges} }}$ ${\displaystyle I_{1}}$ ${\displaystyle I_{2}}$

${\displaystyle I_{\mathrm {ges} }=\sum \limits _{n=1}^{N}I_{n}=I_{1}+I_{2}+\dots +I_{N}}$

By connecting laboratory power supplies in parallel with current limiting , it is possible to achieve a higher direct current than a single device can deliver. Alternating currents from current transformers can also be added in their instantaneous values ​​or subtracted after reversing the polarity of a transformer.

Resistances

Combination of two resistors connected in parallel with the same length and cross-sections and to form a total resistance ${\displaystyle l}$ ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$

The figure on the right shows two resistors , with the same conductivity and their conductance values ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$ ${\displaystyle \sigma }$

${\displaystyle G_{1}=1/R_{1}=\sigma \cdot {\frac {A_{1}}{l}}}$ and ${\displaystyle G_{2}=1/R_{2}=\sigma \cdot {\frac {A_{2}}{l}}}$

and the overall conductance of their parallel connection

${\displaystyle G_{\mathrm {ges} }=\sigma \cdot {\frac {A_{1}+A_{2}}{l}}=G_{1}+G_{2}}$

General for the parallel circuit of resistors applies ${\displaystyle N}$ ${\displaystyle R_{\mathrm {ges} }=R_{1}{\|}R_{2}{\|}\dots {\|}R_{N}}$

${\displaystyle G_{\mathrm {ges} }=\sum _{n=1}^{N}G_{n}=G_{1}+G_{2}+\ldots +G_{N}={\frac {1}{R_{\mathrm {ges} }}}=\sum \limits _{n=1}^{N}{\frac {1}{R_{n}}}}$

The total resistance of resistors connected in parallel with the same resistance value is the same ${\displaystyle N}$ ${\displaystyle R_{1}=R_{2}=\ldots =R_{N}=R}$

${\displaystyle R_{\mathrm {ges} }={\frac {R}{N}}}$

This applies especially to 2 resistors connected in parallel

${\displaystyle R_{\mathrm {ges} }={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}={\frac {R_{1}\;R_{2}}{R_{1}+R_{2}}}}$

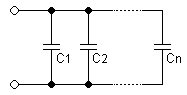
capacities

Combination of two capacitors connected in parallel with the same distance and with the areas and to form a total capacitor ${\displaystyle d}$ ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$

Parallel connection of capacitors

The figure on the right shows two capacitors with the same permittivity and capacitance ${\displaystyle \varepsilon }$

${\displaystyle C_{1}=\varepsilon \cdot {\frac {A_{1}}{d}}}$ and ${\displaystyle C_{2}=\varepsilon \cdot {\frac {A_{2}}{d}}}$

and the total capacity of their parallel connection

${\displaystyle C_{\mathrm {ges} }=\varepsilon \cdot {\frac {A_{1}+A_{2}}{d}}=C_{1}+C_{2}}$

The following generally applies to parallel connections

${\displaystyle C_{\mathrm {ges} }=\sum _{n=1}^{N}C_{n}=C_{1}+C_{2}+\ldots +C_{N}}$

Inductors

Parallel connection of non-coupled coils

Uncoupled ideal coils with the inductances behave like resistors with AC voltage. When connecting in parallel, the rules for parallel resistors can be adopted: ${\displaystyle L_{n}}$

${\displaystyle L_{\mathrm {ges} }=L_{1}{\|}L_{2}{\|}\dots {\|}L_{N}}$

${\displaystyle {\frac {1}{L_{\mathrm {ges} }}}=\sum \limits _{n=1}^{N}{\frac {1}{L_{n}}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\ldots +{\frac {1}{L_{N}}}}$

Impedances, admittances

The parallel connection of impedances or admittances results in the same way as the parallel connection of resistors or conductance values, but the calculation is complex : ${\displaystyle {\underline {Z}}}$ ${\displaystyle {\underline {Y}}}$

${\displaystyle {\underline {Y}}_{\mathrm {ges} }={\frac {1}{{\underline {Z}}_{\mathrm {ges} }}}=\sum \limits _{n=1}^{N}{\frac {1}{{\underline {Z}}_{n}}}=\sum _{n=1}^{N}{\underline {Y}}_{n}}$

${\displaystyle {\underline {Z}}_{\mathrm {ges} }={\underline {Z}}_{1}{\|}{\underline {Z}}_{2}{\|}\dots {\|}{\underline {Z}}_{N}}$

Diodes and light emitting diodes

In the same direction parallel

Light-emitting diodes connected in parallel with a series resistor

Diodes can only be connected in parallel under certain conditions, when the current would overload a single diode. Since the forward voltage decreases with increasing temperature, an even current distribution is only guaranteed if:

• the diodes come from the same production batch,
• the diodes are thermally coupled to one another (e.g. on a common heat sink).

As a rule, each diode has to be linearized via its own series resistor. Although this increases the losses, it prevents an uneven current distribution in the diodes.

Anti-parallel

Diodes connected in anti-parallel

Diodes connected in anti-parallel are parallel to one another in opposite directions (anode to cathode and vice versa). Such circuits are used, for example, to limit the voltage of an alternating voltage to the value of the forward voltage (approx. 0.7 V for silicon diodes). Furthermore, for example, a light-emitting diode with an anti-parallel protective diode can be operated with alternating voltage or (with anti-parallel connection with an LED of a different color) indicate a polarity change.

Anti-parallel interconnected diodes were also used as so-called hearing protection diodes or hearing protection rectifiers in landline telephones and the headphones that were common at the time from the middle to the end of the 20th century ; With their non-linear but “soft” characteristic, they limited clicking noises to a tolerable level without causing strong distortions in loud conversations.

Bipolar transistors

The same bipolar transistors can only be connected in parallel to increase the current if the emitter resistors (negative current feedback) in each branch ensure that the current is distributed equally well. The cause is a base-emitter voltage which decreases with increasing temperature, which increases the base current and consequently the collector current, as well as increasing current gain. Close thermal coupling is also helpful. The base and collector connections can be connected in parallel under these conditions.

MOSFET and IGBT

Similar power MOSFET and IGBT can be paralleled in switching operation because their temperature characteristic leads to a constant current sharing. Nevertheless, it usually makes sense to insert a resistor with a small value (approx. 0.1–0.5 Ω) in order to optimize the load distribution. The Joule heat of the resistor must be taken into account when dimensioning . The above only applies to switching operation. In analog operation, the negative temperature coefficient of the gate threshold voltage means that only one of the transistors takes up the entire current. Since the spread of the gate threshold voltage can turn out to be very large, relatively large drain resistances (compared to bipolar transistors) are required to compensate for these differences.

Gas discharge lamps

Gas discharge lamps cannot be connected directly in parallel; due to its negative differential internal resistance (see gas discharge ) only one of them would light up. Gas discharge lamps need to set a ballast or a series resistor for current limiting. Together with this ballast, they can be connected in parallel like other consumers.

See also

• More circuits

Web links

• Virtual experiment on electrical parallel connection of two ohmic resistors - experiments and physics didactics

Individual evidence

1. ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary
2. ↑ Kurt Bergmann: Electrical measurement technology: Electrical and electronic processes, plants and systems. Vieweg, 5th ed. 1993, p. 99