Electric voltage
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Electric voltage | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
The electrical voltage (often simply referred to as voltage ) is a fundamental physical quantity in electrical engineering and electrodynamics . Your formula symbol is that . In the international system of units, it is given in the unit volt ( symbol : V). To identify a time dependency, the lower case letter is used for the instantaneous value of the voltage. The formula symbol is used in Anglo-Saxon .
Put simply - and suitable for everyday electrical circuits - the voltage characterizes the “strength” of a voltage source ; it is the cause of the electric current that transports the electric charge . If, for example, the two poles of a battery or a socket are connected to one another by an electrically conductive component , current flows. The size of the electric current depends on the size of the voltage and on a property of the conductive component called electrical resistance . In reverse, a voltage occurs on a body through which current flows, which is then called a voltage drop or voltage drop. Using the electro-hydraulic analogy , one can imagine the voltage that drives the electrical charge through the conductor as the pressure difference between two points in a pipe that drives the liquid through the pipe.
According to the physical principles, voltage expresses the ability to shift charges so that a current flows through the connected consumer and work is performed. The electrical voltage between two points is defined as the line integral of the electrical field strength along a specified path from one point to the other. It is also the difference in the potential electrical energy that a charge has at the two points in relation to this charge. This is also simply referred to as “voltage = energy per charge”.
Electric voltage is created in a “natural” way, for example through friction , during the formation of thunderstorms , through ion transport through a biomembrane and during chemical redox reactions . For technical purposes, voltages are mostly generated by electromagnetic induction and electrochemical processes .
There is a wide range of electrical voltages . It can cause currents that are life-threatening for humans .
- ↑ Note: Here, however, there is a risk that the symbol V is confused with the associated unit symbol V for volts .

definition
The electrical voltage between two points A and B in an electrical field with the field strength is defined as the spatial line integral along a specified path from point A to point B.
- .
In this field there is a charge that is assumed to be so small that it does not change the existing field with its field. An object loaded with is moved from A to B over a given path. The cause of the movement of the object is irrelevant for the definition.
A force acts on this charge , so that work is done during movement . With "work equals force times distance" applies to a place-dependent force and direction of movement for this work .
This results in a statement that is equivalent to the voltage definition above
- .
The sign of results from the signs of work and charge. The work is negative if the field absorbs energy from the charged object when it moves from A to B, it is positive if field energy transfers to the test charge. Because the voltage is related to , it becomes a parameter of the electric field that is independent of the amount and sign of the test charge.
This voltage definition applies to all electric fields, i.e. both for eddy fields and for eddy-free (potential) fields. In vortex fields, the tension generally depends on the path.
However, if an electric field is a source or potential field (see also conservative force ), the work for the displacement of a charge from one place to another is independent of the path between the two places. The voltage is therefore only dependent on the end points of the integration path. This is the case in electrostatics and in many areas of electrical engineering, which is what gives the term electrical voltage its typical practical meaning: One speaks not only of the electrical voltage between two points A and B, but also of the electrical voltage between two (ideal ) Ladders or poles A and B. In general, the following applies .
Electrical potential
Symbols for the electrical potential are and . This potential at a point P in space by means of the electric field strength and the magnetic vector potential defined by
- with the remark: The electrical potential is not unique, because any constant scalar quantity can be added to a given potential without changing its gradient.
For the sake of clarity, a reference point P 0 is defined, which receives the zero potential . In many areas there are conventions for the choice of the reference point, so that it is often not mentioned in the language. In electrical engineering , the reference point is placed on the section of conductor that is referred to as “ground” ; in the theory of electric fields the reference point is often placed “into infinity”.
The integral value with respect to the reference point P 0 is referred to as the electrical potential.
- .
With the potentials and at points A and B results from the definition of the voltage
- .
Is in a potential field . In the following explanations, only the electrical voltage in a potential field is assumed. Apply there
- .
The electrical voltage between these locations is consequently equal to the difference in the electrical potentials at these locations.
The specification of a voltage at one point is only possible in exceptional cases if the second point for the voltage is known from the circumstances; otherwise the voltage can only be given between two points. In contrast to this, the potential only depends on the selected point in space and can therefore be specified as a location-dependent function. It thus represents a scalar field which can be determined from the electrical field (except for a constant) and, conversely, clearly determines the electrical field.
Positive charge carriers move - if no other forces act on them - in the direction of the field strength. Because they lose potential energy in the process, the electrical potential decreases in this direction. Negatively charged objects, on the other hand, move against the field strength in the absence of other forces, in the direction of increasing potential.
In the case of a displacement along an equipotential line , the integral is equal to zero, because it stands on this path , so that the scalar product is equal to zero.
If a charge is transported from A to B and back to A via any other route, the ring integral disappears in the potential field over the closed cycle:
Counting direction
If a device is able to build up a voltage, it is called a voltage source; the voltage is also called the source voltage . Otherwise the device is an electrical consumer ; the voltage is then also called the voltage drop. Since the voltage is a scalar quantity , the voltage arrows used in the representations only determine the sign. You can arbitrarily set a direction of rotation in a mesh . Then a voltage with an arrow pointing in the direction of the orbit is to be set positive and otherwise negative.
The following two drawings can be thought of as connecting points A with A and B with B to form a circuit , through which an electric current can flow.
The direction of the electric current is defined as the direction in which positive electric charge moves, see direction of electric current . A certain direction is also useful for alternating current if current arrows are to show the direction of the energy flow; the voltage arrows result in the same way as for constant quantities.
The following table shows the definition of direction that is largely arbitrary in electrical engineering. There are certainly applications in which it is advisable to set the voltage direction (for a given current direction) in the opposite direction, see counting arrow . In electrocardiography , for example, voltages in the direction of increasing potential are evaluated positively so that the direction of the voltage arrow corresponds to the projection of the summed dipole moment .
Connections
Both the voltage itself and the relationships with other quantities in the electrical circuit are illustrated with the help of didactic models. For the voltage, the analogy to altitude energy (as the "drive" of balls or skiers sliding down) and the electro-hydraulic analogy (with the pressure difference between two points of a pipeline as the "drive" of the liquid) are widespread.
Electric voltage with amperage
If there is an electrical voltage between two points, there is always an electrical field that exerts a force on charge carriers. If the points are located on an electrically conductive material in which the charge carriers are movable, the voltage causes a directional movement of the charge carriers and an electric current flows. Is the electrical current strength proportionally linked to the electrical voltage as is the case with most metals, i.e. if
Then one obtains Ohm's law with the proportionality factor
Wherever the proportionality applies to every instantaneous value at equal sizes as with alternating quantities , is the resistance factor to emphasize its ideal form as a constant and ohmic resistance .
In the case of inductances and capacitances, the current intensity is also sinusoidal with sinusoidal voltage, but the phase angle of the current intensity is shifted compared to the voltage . Ohm's law does not apply to the instantaneous values , but to the effective values and peak values . In this respect, such a component counts as a linear resistance . The proportionality factor is called impedance . With regard to instantaneous values, an Ohm's law of alternating current technology can be used for the description , with the complex impedance of the component providing the proportionality factor
Nonlinear components, in which the resistance depends on the instantaneous voltage, obey more complicated laws, for example in the case of the ideal diode of the Shockley equation .
Electric voltage with power and energy
The electrical charge can be viewed as a property of an elementary particle and thus as a quantized quantity or, outside of atomic structures, as a rule as a continuous and differentiable quantity (see electrical charge # quantum character ). When a quantity of charge flows through a resistor, energy is converted due to the work of displacement . From the definition equation for the voltage
and from the relationship between charge and electric current
surrendered
From the definition of the service follows further
and especially with ohmic resistances with results
Electrical voltage on the voltage and current divider
Voltage divider
In the illustration opposite, the upper circuit shows a voltage divider that consists of exactly one cycle. According to the rule of stitches applies
The source voltage is equal to the sum of the partial voltages, and in the case of ohmic resistors the voltage across each of the resistors is less than the source voltage. How the voltage is distributed across the resistors results from the fact that the current does not branch in this circuit and therefore flows with the same strength everywhere in the mesh . This is what Ohm's law says
The ratio of the partial voltages is thus equal to the ratio of the associated ohmic resistances
Flow divider
The circuit below shows a current divider where the source and each of the resistors are on the same line at the top and bottom, so that the same voltage is dropped across all three components .
Measurement of electrical voltage
The voltmeter used to measure a voltage is connected in parallel to the object whose voltage is to be measured.
When using a moving-coil measuring mechanism , which is physically an ammeter, a current divider circuit is created for voltage measurement . The current is measured through the internal resistance of the measuring device as a measure of the voltage. Since every measuring device has a limited measuring range , if the maximum measurable value is exceeded, the current must be reduced via a series resistor and the measuring range expanded.
The measurement deviation caused by the current branching (the feedback deviation due to the measuring device) is kept small if it is large compared to the measurement object . Only in this way does the total resistance of the measuring circuit remain almost unchanged and the measuring circuit has negligible influence on the rest of the circuit. The factor is introduced here for comparison
With a parallel connection , the currents in the parallel branches add up to the total current and the conductance values of the branches add up to the total conductance .
and with the use of results in
Becomes the term of the relative measurement error
transferred to this circuit with the correct value and the value deviating therefrom , the result is
If, for example, it is required for this always negative deviation that should be, then it must be. If is 100 times as large as , then is 1% smaller than .
If the current from A to B comes from a constant current source, in this case the voltage is measured with a relative deviation = -1%. If there is a constant voltage source between A and B , = 0. With every other supply, the measurement deviation is in between.
If the relative deviation is given that someone is ready to accept, the requirement for the resistance in the measurement branch is:
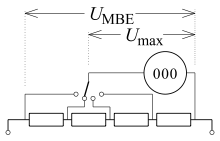
With electronic voltage measuring devices (digital measuring device , oscilloscope or compensation measuring recorder ) it is not usual to extend the measuring range with a series resistor; the internal resistance of these measuring devices is typically 1 to 20 MΩ in all ranges. The series resistance would be of an order of magnitude that could not be reliably implemented. Instead, a voltage divider must be used if the maximum measurable voltage value is exceeded . At a tap located further to the right in the adjacent circuit, a lower voltage can be fed to the indicating part, thus increasing the measuring range end value .
The problem that the measuring device is switched too parallel as above , and thus the total resistance of the measuring circuit is changed, is the same as above with the measurement with a moving-coil measuring mechanism. Only the series resistor , which varies in size depending on the measuring range, is omitted.
Classification
Time dependence
Time-dependent quantities can periodically be time-dependent quantities, transition quantities or random quantities. Periodic voltages occur in the form of an alternating voltage or mixed voltage . Another point of view is to distinguish between harmonic voltage ( sinusoidal voltage ) and non-harmonic voltage (e.g. square wave voltage ).
The non-periodically time-dependent variables include, among other things, pulses , switching jumps or stochastic variables. They are usually difficult to describe mathematically or not at all.
Voltages that do not change their value over a longer period of time are referred to as direct voltage .
Voltage level
The European standardization are three voltage levels:
- Low voltage (AC voltage ≤ 50 V and DC voltage ≤ 120 V)
- Low voltage (AC voltage> 50 V to ≤ 1000 V and DC voltage> 120 V to ≤ 1500 V)
- High voltage (AC voltage> 1000 V and DC voltage> 1500 V)
The data apply to AC voltage for the effective value , otherwise for harmonic-free DC.
Within high voltage, a further distinction is made between medium voltage , high voltage and maximum voltage .
Imprinted tension
A voltage that appears on a component depends on the internal structure of the voltage source . Your source resistance forms a voltage divider with the component resistance. The voltage established at the “load” of the source is less than the open circuit voltage to an uncertain extent , as long as the resistances are not known. Batteries , accumulators , almost all power supply units and other electronic power supply circuits deliver a constant voltage - in the sense of load-independent voltage -, for example 12 V (fixed up to a maximum permissible current strength). In this case we speak of an impressed voltage.
AC voltage is also referred to as impressed voltage, for example 230 V in the Central European low-voltage network, if only the current changes when the load changes.
AC voltage technology
AC voltage is by definition periodic and does not contain any direct component . AC voltage technology mainly deals with applications in energy and communications technology .
The information on the definition and all the following quantities correspond to the standardization .
Characteristic values
To describe an alternating voltage, it is often necessary to know its course over time; an oscilloscope is required to measure it . This shows:
-
= Period duration or short period;
- for non-harmonic processes: period of the fundamental oscillation
- = Maximum value (general), peak value (with AC voltage)
- = Minimum value
- = Peak-valley value
or to calculate elementary:
- = Frequency
- = Angular frequency (with sinusoidal shape)
Given the large number of time curves of voltages with different curve shapes, averaged values that can be determined with simpler voltage measuring devices are used for an initial assessment of how they work in comparable applications . There are also several evaluation factors.
Averaged values
| designation | formula | description |
|---|---|---|
| Equivalence | The equivalent of a voltage is the arithmetic mean value of this voltage in the time interval of the period . With alternating voltage this is by definition equal to zero. | |
| Rectified value | The rectification value of a voltage is the arithmetic mean of the amount of this voltage. | |
| Rms value | The rms value is the root mean square value of this voltage. |
Evaluation factors
| designation | formula | description | rating |
|---|---|---|---|
| Crest factor | The crest factor (also known as the crest factor) describes the relationship between the peak value and the rms value of an alternating electrical quantity . | The larger the crest factor, the more "bizarre" the voltage curve; | |
| Form factor | The form factor describes the ratio of rms value to rectified value of a periodic signal. | The larger the form factor, the more "bizarre" the voltage curve; | |
| Vibration content | In the case of mixed voltage, the vibration content is the ratio of the effective value of the alternating voltage component to the effective value of the total voltage . | The smaller the vibration content, the closer the voltage approaches a DC voltage; | |
| Ripple | In the case of mixed voltage, ripple is the ratio of the effective value of the alternating voltage component to the amount of the equivalent value. | The smaller the ripple, the closer the mixed voltage approaches a DC voltage; | |
| Distortion factor | In the case of non-harmonic oscillations, the harmonic distortion indicates the extent to which harmonics , which are superimposed on a sinusoidal alternating quantity, contribute to the overall signal. = Rms value of the total voltage; = RMS value of their fundamental oscillation. |
The smaller the distortion factor, the “purer” the sinusoidal oscillation; |
AC harmonic voltage
In electrical engineering, the sine function , which is also known as the harmonic function, has the greatest importance alongside all other possible functions. The reasons for this are listed under alternating current .
For the mathematical description using the View as real-valued Size
- or
or - in many cases calculations simplistic - View as complex- size
with = phase angle ; = Zero phase angle ; = imaginary unit ( )
The averaged values are independent of frequency and zero phase angle
- Rectified value of the sinusoidal voltage:
- RMS value of the sinusoidal voltage:
hazards
Although the current strength per body area, i.e. the current density , as well as the duration of exposure are responsible for the effects of an electrical accident , the voltage is usually given as an indication of possible dangers. In the case of voltage sources , this voltage can be easily quantified, while the current strength - for example through a body that comes into contact with cables - can only be calculated indirectly (in simple cases with the aid of Ohm's law ) and depends heavily on the specific situation (for example, the body resistance and frequency). In addition, the level of the voltage determines the minimum distance to bare , uninsulated electrical conductors because of potential flashovers.
The general rule is: 50 V AC or 120 V DC are the maximum permissible contact voltage .
Tension in Chemistry and Nuclear Physics
Electrical voltages in electrochemistry are mostly in the lower single-digit volt range. For each reaction there is a standard potential as the difference between the electrode potentials . Their concentration dependencies are described with the Nernst equation .
Electrical voltages in nuclear physics are used to accelerate electrically charged particles ; the voltages are in the high voltage range from a few tens of kilovolts to a few megavolts. The unit of measurement " electron volt" used in this context, however, is not a voltage, but an energy unit: 1 electron volt (also electron volt; unit symbol eV) corresponds to the (kinetic) energy of the elementary charge (e.g. of a single electron) in an electrical Field was accelerated by a voltage of 1 volt.
literature
- Gert Hagmann: Fundamentals of electrical engineering. Aula-Verlag, Wiebelsheim 2006, ISBN 3-89104-707-X .
- Helmut Lindner , Harry Brauer, Constans Lehmann: Paperback of electrical engineering and electronics. 8., rework. Edition. Fachbuchverlag, Vienna et al. 2004, ISBN 3-446-22546-3 .
- Ralf Kories, Heinz Schmidt-Walter: Pocket book of electrical engineering. 7th, exp. Edition. German, Frankfurt am Main 2006, ISBN 3-8171-1793-0 .
- Heinrich Frohne, Karl-Heinz Locher, Hans Müller: Fundamentals of electrical engineering. 20th, revised. Edition. Teubner, Stuttgart et al. 2005, ISBN 3-519-66400-3 .
- Siegfried Altmann, Detlef Schlayer: Teaching and exercise book electrical engineering. 3rd, arr. Edition. Fachbuchverlag, Vienna et al. 2003, ISBN 3-446-22683-4 .
- Manfred Albach: Periodic and non-periodic signal forms. Basics of electrical engineering. Pearson Studium, Munich et al. 2005, ISBN 3-8273-7108-2 .
Web links
- Clear explanation of the term voltage with a water model
- Electric voltage explained at student level ( LEIFI )
- Multimedia online lesson Electrical Voltage (Telekolleg Physik 16, Bayerischer Rundfunk)
References and comments
- ↑ a b DIN 1304-1: 1994 formula symbols .
- ↑ a b EN 60027-1: 2007 Formula symbols for electrical engineering .
- ↑ a b DIN 5483-2: 1982 Time- dependent quantities .
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary entry 121-11-27.
- ↑ a b DIN 1324-1: 2017 Electromagnetic Field - Part 1: State variables .
- ^ Moeller: Fundamentals of electrical engineering . Springer-Verlag, 2013, ISBN 978-3-663-12156-5 , pp. 139 ( google.com ).
- ↑ Ekbert Hering, Rolf Martin, Martin Stohrer: Physics for engineers . Springer Vieweg, 12th ed. 2016, p. 241
- ↑ IEC 60050, see International Electrotechnical Dictionary entry 121-11-25.
- ↑ EN 80000-6: 2008 Quantities and units - Part 6: Electromagnetism ; Entry 6-11.
- ↑ DIN EN 60375: 2004 Agreements for electrical circuits and magnetic circuits ; Cape. 6.1 and 6.2.
- ↑ IEC 60050, see International Electrotechnical Dictionary entry 131-12-04.
- ^ Helmut Haase, Heyno Garbe, Hendrik Gerth: Fundamentals of electrical engineering . 3. Edition. Schöneworth, 2009, ISBN 978-3-9808805-5-8 , 8.8 Analogy of current and pump circuit.
- ↑ For further illustrations see z. B. Jan-Philipp Burde (2018): Conception and evaluation of a teaching concept for simple electrical circuits based on the electron gas model; Studies on physics and chemistry learning, Volume 259, Logos-Verlag, Berlin, ISBN 978-3-8325-4726-4 , Online , pp. 62–72
- ↑ EN 80000-6; Entry 6-46.
- ↑ DIN 1311-1: 2000 Vibrations and vibratory systems .
- ↑ DIN EN 50110-1: 2005 (VDE 0105-1) Operation of electrical systems .
- ↑ DIN 40110-1: 1994 alternating current quantities .
- ↑ VDE 0100, see TAEV 2004 IV / 1.1.