Rectified value

The arithmetic mean value of a variable is zero and is therefore not suitable for characterizing a variable. The easiest way to obtain quantitative information about an alternating quantity is its rectified value . This term used in electrical engineering stands for the mean value of the amount of this quantity ( average rectified value ( ARV )).

The rectified value is preferably used for alternating current or alternating voltage .

introduction

The rectified value of an alternating current indicates which direct current transports the same amount of charge as a rectified alternating current on average over time.

The mathematical definition is:

${\displaystyle {\overline {\left|x\right|}}={\frac {1}{T}}\int _{0}^{T}|x(t)|\mathrm {d} t}$

If the course of the signal cannot easily be described mathematically, the following approximation method can be used to calculate the rectification value

${\displaystyle {\overline {\left|x\right|}}\approx {\frac {1}{n}}\sum _{i=1}^{n}|x_{i}|={\frac {1}{n}}\left(|x_{1}|+|x_{2}|+|x_{3}|+\dotsb +|x_{n}|\right)}$

where samples or instantaneous values are read from the signal at a constant interval during a period . It is ${\displaystyle x_{i}}$ ${\displaystyle \Delta t}$ ${\displaystyle T}$

${\displaystyle \Delta t={\frac {T}{n}}\ .}$

The order - first the amount, then the mean value - must not be mixed up. Therefore it must be recognizable by the spelling (see above). The spellings (wrong order) and (unclear order) should be avoided . ${\displaystyle \left|{\overline {x}}\right|}$ ${\displaystyle |{\overset {-}{x}}|}$

In the case of a sinusoidal alternating variable, which occurs particularly frequently, the rectification value is (2 / π) times the maximum value ( peak value ).

Application in measurement technology

Display measuring devices in measurement technology have to work so slowly that the measured values can be read. In the case of rapid changes that the human eye cannot detect, they show an average value, e.g. B. electromechanically averaged with moving-coil measuring mechanism , electronically averaged with dual-slope method , see also digital measurement technology . However, the mean value of an alternating quantity is zero (according to the definition of an alternating quantity, see). The simplest way to measure the alternating quantity is to measure its rectified value . A more complex option is to measure its effective value . From a physical point of view, this is the direct current equivalent in terms of the active power of the alternating quantity. In technology, the effective value is much more important; Alternating quantity measuring devices are designed to display this value.

Nevertheless, measuring devices forming the rectifying value are widespread. However, they do not show the rectified value, but 1.11 times it. In the case of a sine curve, this is the effective value, see "Comparison" below. The devices thus display the rms value - based on the detection of the rectified value. The only thing that makes sense and is correct is for the sinusoidal curve, which, however, occurs in many alternating variable measurement tasks. For any other signal course, the use of the devices is questionable or pointless, see below under “Consequence”.

The measurement of an alternating signal on which a direct signal is superimposed is also questionable or even pointless, see below under "Mixed voltage". For this reason, with some measuring devices there is the additional option of recording the change component alone.

Derivation

The mean value is determined in a signal-time diagram from the area that extends in height between the signal line and the zero line and in width over the duration of a full period. A rectangle with the same area and width has the mean height of the area; this height is the mean. The area is determined by integration, for a rectangle by multiplication.

Correspondingly, the rectified value results from the area of ​​the rectified signal; that means ${\displaystyle x_{\mathrm {glr} }}$

${\displaystyle x_{\mathrm {glr} }\cdot T=\int _{0}^{T}|x(t)_{\mathrm {signal} }|\mathrm {d} t}$

This gives the formula

${\displaystyle x_{\mathrm {glr} }={\frac {1}{T}}\int _{0}^{T}|x(t)_{\mathrm {signal} }|\mathrm {d} t}$

Special results can be derived from this general form, as shown below.

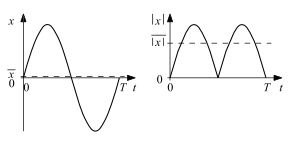
Sine magnitude

Sine value with mean value
Rectified sine value with associated mean value

A sinusoidal alternating quantity, or sine quantity for short, is sufficient for the equation

${\displaystyle x(t)_{\mathrm {signal} }={\hat {x}}\cdot \sin(\omega t+\varphi _{x})}$

Since the area is to be formed over a whole period of the function, this is independent of the starting point of the area. A zero phase angle need not be taken into account; it is set to 0 for the sake of simplicity. ${\displaystyle \varphi _{x}}$

${\displaystyle x_{\mathrm {glr} }={\frac {1}{T}}\int _{0}^{T}|{\hat {x}}\cdot \sin(\omega t)|\mathrm {d} t}$

As the picture shows, the rectified signal is already periodic, so that the calculation can be carried out with instead . ${\displaystyle T/2}$ ${\displaystyle T/2}$ ${\displaystyle T}$

${\displaystyle x_{\mathrm {glr} }={\frac {1}{\frac {T}{2}}}\int _{0}^{\frac {T}{2}}|{\hat {x}}\cdot \sin(\omega t)|\mathrm {d} t}$

In is so that the amount symbol can be omitted. ${\displaystyle 0\leq t\leq T/2}$ ${\displaystyle \sin(\omega t)\geq 0}$

${\displaystyle x_{\mathrm {glr} }={\frac {2{\hat {x}}}{T}}{\bigg [}-{\frac {1}{\omega }}\cos(\omega t){\bigg ]}_{t=0}^{\frac {T}{2}}}$

With will ${\displaystyle \omega ={\frac {2\pi }{T}}}$

${\displaystyle x_{\mathrm {glr} }={\frac {\hat {x}}{\pi }}{\bigg [}-\cos(\omega t){\bigg ]}_{\omega t=0}^{\pi }}$

With simplifies that too ${\displaystyle \cos(0)=1;\ \cos(\pi )=-1}$

${\displaystyle x_{\mathrm {glr} }={\frac {\hat {x}}{\pi }}(1+1)={\frac {2}{\pi }}{\hat {x}}=0{,}6366\cdot {\hat {x}}}$

Trimmed sine wave voltage

Cut sinusoidal voltage; original and rectified

The voltage, which is often caused by phase control and shown on the left in the adjacent picture, is essentially a sinusoidal voltage, but after each zero crossing it remains at zero, and the sinusoidal curve is only switched on again after a while . For this tension results ${\displaystyle aT}$

${\displaystyle u_{\mathrm {glr} }={\frac {2}{T}}\int _{aT}^{\frac {T}{2}}|{\hat {u}}\cdot \sin(\omega t)|\mathrm {d} t}$

${\displaystyle u_{\mathrm {glr} }={\frac {\hat {u}}{\pi }}\left[1+\cos(2a\pi )\right]}$

with 0 ≤ <½. ${\displaystyle a}$

Pulsed tension

Periodically switched on and off voltage with mean value
Its alternating component and rectified alternating component with mean values

The voltage shown in the adjacent picture is a mixed voltage ; it arises from a positive DC voltage that is switched on periodically for the duration and switched off for the rest of the period duration . Since there are no negative instantaneous values ​​here, the mean value and rectified value are equal; ${\displaystyle u}$ ${\displaystyle aT}$ ${\displaystyle U}$

${\displaystyle {\overline {u}}=u_{\mathrm {glr} }=U\cdot a}$

with 0 ≤ ≤ 1. The borderline cases = 0 and = 1 supply the voltage that is never switched on and the voltage that is always switched on. ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle a}$

${\displaystyle {\overline {u}}}$ is the direct component of the mixed voltage, which is superimposed by an alternating component.

Bill of exchange

The picture below left shows the alternating component of the pulsed voltage. Here again the mean value = 0. ${\displaystyle u_{\mathrm {we} }=u-{\overline {u}}}$ ${\displaystyle {\overline {u_{\mathrm {we} }}}}$

The course shown next to it is obtained by rectification; the rectified value is obtained from its mean value. The area during the duration of a period consists of two rectangles, each of which has the size . So that ${\displaystyle U\;T\cdot a(1-a)}$

${\displaystyle u_{\mathrm {we\ glr} }=U\cdot 2a(1-a)}$

Mixed voltage

Superposition of direct and alternating voltage

There are two cases of mixed voltage.

1. In the picture on the left, the constant component (in terms of its amount) is greater than the peak value of the alternating component . The curve does not intersect the zero line. In this case the rectified value is equal to the amount of the direct component. It does not contain any information about the exchange rate. ${\displaystyle u_{\mathrm {gl} }}$ ${\displaystyle {\hat {u}}_{\mathrm {we} }}$

${\displaystyle u_{\mathrm {glr} }={\overline {|u|}}=|u_{\mathrm {gl} }|}$

2. In the picture on the right, the constant component (in terms of its amount) is smaller than the peak value of the alternating component . The curve intersects the zero line. In this case, determining a rectification value does not make sense; it contains neither a statement about the constant component nor the alternating component nor their ratio. ${\displaystyle u_{\mathrm {gl} }}$ ${\displaystyle {\hat {u}}_{\mathrm {we} }}$

Other waveforms

For rectified values ​​for some other signal curves, see the table under form factor .

Comparison of effective value with rectified value

The ratio of rms value to rectified value is known as the form factor

${\displaystyle k_{f}={\frac {x_{\mathrm {eff} }}{x_{\mathrm {glr} }}}}$

With this, the curve shape of an alternating or mixed variable can be assessed. It is ≥ 1 and the greater the “bizarre” the course.

For sine size

Rectified value:	${\displaystyle x_{\mathrm {glr} }={\frac {2}{\pi }}{\hat {x}}=0{,}6366\cdot {\hat {x}}}$
Effective value:	${\displaystyle x_{\mathrm {eff} }={\frac {1}{\sqrt {2}}}{\hat {x}}=0{,}7071\cdot {\hat {x}}}$
Form factor:	${\displaystyle k_{f}={\frac {\frac {1}{\sqrt {2}}}{\frac {2}{\pi }}}={\frac {\pi }{2\cdot {\sqrt {2}}}}={\frac {\pi }{\sqrt {8}}}=1{,}111}$

For cut sine voltage

Rectified value:	${\displaystyle u_{\mathrm {glr} }={\frac {1+\cos(2a\pi )}{\pi }}{\hat {u}}}$
Effective value:	${\displaystyle u_{\mathrm {eff} }={\sqrt {{\frac {1}{2}}-a+{\frac {1}{4\pi }}\sin(4a\pi )}}\ {\hat {u}}}$
Form factor:	The equation is omitted because nothing can be shortened.
	When a = 1/4 (switching on at the apex) ${\displaystyle k_{f}={\frac {\pi }{2}}=1{,}571}$

For pulsed tension

The borderline case = 0 delivers = 0 and is excluded from the comparison. ${\displaystyle a}$ ${\displaystyle u}$

Rectified value:	${\displaystyle u_{\mathrm {glr} }=U\;a}$
Effective value:	${\displaystyle u_{\mathrm {eff} }=U{\sqrt {a}}}$
Form factor:	${\displaystyle k_{f}=1/{\sqrt {a}}}$

For alternating portion of the pulsed voltage

The borderline cases = 0 and = 1 do not contain any change and are excluded. ${\displaystyle a}$ ${\displaystyle a}$

Rectified value:	${\displaystyle u_{\mathrm {we\ glr} }=U\;2a(1-a)}$
Effective value:	${\displaystyle u_{\mathrm {we\ eff} }=U{\sqrt {a(1-a)}}}$
Form factor:	${\displaystyle k_{f}=1/\left({2{\sqrt {a(1-a)}}}\right)}$
	For the case of the symmetrical pulse with = ½ = 1, for every other case> 1. If z. B. the voltage is only switched on for 1% of the time, = 5.0. ${\displaystyle a}$ ${\displaystyle k_{f}}$ ${\displaystyle k_{f}}$

Metrological consequence

A measuring device forming the rectified value can result in a considerable measurement error, as it is scaled and adjusted in such a way that the displayed value should be an effective value.

Displayed value:	${\displaystyle x_{a}=1{,}11\cdot x_{\mathrm {glr} }}$
Correct value:	${\displaystyle x_{r}=x_{\mathrm {eff} }=k_{f}\cdot x_{\mathrm {glr} }}$
Relative error:	${\displaystyle f={\frac {x_{a}-x_{r}}{x_{r}}}={\frac {1{,}11}{k_{f}}}-1}$
For = 1.00 ${\displaystyle k_{f}}$	${\displaystyle f}$ = + 11%	Display clearly too big
For = 1.11 ${\displaystyle k_{f}}$	${\displaystyle f}$ = ± 0	Display free of waveform errors
For = 1.57 ${\displaystyle k_{f}}$	${\displaystyle f}$ = - 29%	Display much too small
For = 5.0 ${\displaystyle k_{f}}$	${\displaystyle f}$ = - 78%	Display catastrophically too small;
		only 22% of the effective value are displayed.

Care should therefore be taken when using these devices. The relative error due to the shape of the curve can easily exceed the "a few percent" range. The sinus shape is most likely to be found with the voltage in the power supply network; that is where these devices are used. But even the mains voltage is distorted by the multitude of electronic, non-linear loads. Even more so, the current consumption from the network is often so strongly distorted that measuring the rectification value cannot make a reasonable statement about the current strength.

literature

Many textbooks on measurement technology or electrical engineering, for example

• Kurt Bergmann: Electrical measurement technology. Vieweg, 2000, 6th edition, p. 18.
• Wilfried Weißgerber: Electrical engineering for engineers 2. Springer Vieweg, 2013, 8th edition, p. 2.

Individual evidence

1. ↑ ^{a b} DIN 40110-1: 1994