Digital measurement technology

The measurement technology can be broken down according to different aspects. One possibility is to differentiate between analog and digital measurement technology. Specific sub-areas of digital measurement technology are its measurement method, information display and device technology.

Basics - Definitions - Comparisons

Measurement methods

The measurement is the execution of planned activities for the quantitative comparison of the measured variable with a unit ( DIN 1319-1, No. 2.1). What makes this measurement a digital one should be described by comparing it with analog measurement.

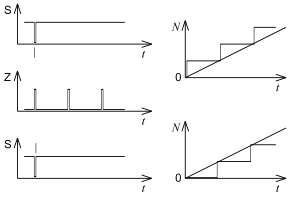
Analog measurement method

Linguistic basis: analog = corresponding.
The measured value is represented by an analog, a similar or corresponding (analog) fact, here by an intermediate value, the value of which can easily be read as a number. ¹)

Example: Moving coil ammeter : The current causes a mark on a scale to be shifted . The length or angle that is continuously assigned to the current is read off.

Every gauge has a gauge drift as a result of imperfection in design, manufacture and adjustment , writable by

1. Guarantee error limits (a lower value is possible by correcting with a curve of the measurement deviations, which have been determined from the difference to better devices or another benchmark),
2. Measurement uncertainty (a lower value is possible due to finer scale divisions, greater experimental experience and repeated measurements).

If one ignores these deviations in order to recognize the essentials, one recognizes as features:

• The output signal (distance or angle) can be resolved as finely as desired .
• It is a clearly reversible measure for the input signal.

Further examples of analog measurement methods:

• Temperature : expansion of the thermometric fluid
• Pressure : deformation of a membrane
• Speed : voltage of a tachometer generator

The measuring device provides the analog, the observer uses it to determine the numerical value and, together with the unit, the measured value.

¹) This sentence is only to be understood as a clear introduction.

Digital measurement method

Linguistic basis: digit (us) = finger, number. ²)
The measured value is shown directly in numerical form. ¹)

Example tachometer

A device that

• one counter advances by one per revolution and
• allows counting for exactly one minute.

The counter reading provides the measured value in units of revolutions per minute.
Note: The special name revolution is widely used as a unit in the specification for rotating machines instead of the one. Correspondingly, the units of revolution per second or revolution per minute are widely used for rotational speed.

Digital Wheatstone Bridge

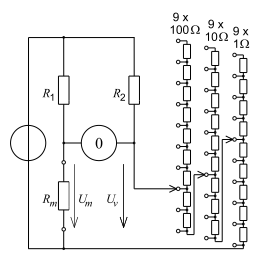
Example Wheatstone Bridge

Setting of the resistance decades up to the " zero adjustment ", more precisely up to

${\displaystyle -U_{q}/2\leq U_{m}-U_{v}\leq U_{q}/2}$ .

This is the smallest adjustable voltage step. If is, then after the adjustment the resistance to be measured is equal to the resistance set on the decade switches. The picture shows: ${\displaystyle U_{q}}$ ${\displaystyle U_{v}}$ ${\displaystyle R_{1}=R_{2}}$ ${\displaystyle R_{m}}$

${\displaystyle R_{m}}$ = whole number times smallest step size = 235 × 1 Ω.

Here, too, deviations from the measuring device must be observed,

1. Guarantee error limits through the error limits of the built-in benchmark,
   • in the example counter: the time scale,
   • in the example bridge: the resistors used,
2. Measurement uncertainty due to a digit in the least significant place. This quantization or digitization deviation can always be made insignificantly small as a relative deviation if it is possible to work with large numbers, see below "On the quantization deviation".

If one ignores these deviations in order to recognize the essentials, one recognizes as features:

• The output signal is in a countable number of steps can be subdivided .
• It is a clear statement in itself.

The measured variable can be subject to any fine changes; the measuring device quantizes its measured value ,

• in the example counter: the value of the speed by the pulse generator,
• in the example of a bridge: the value of the resistance through the step-by-step setting of the reference resistance . ${\displaystyle R_{m}}$

¹) This sentence is only to be understood as a clear introduction.

²) The term digit is not used uniformly in the literature, often in the sense of a digit, occasionally in the sense of a digit.

To the quantization deviation

It is possible to arrive at a large number of the measured value and thus a small relative quantization deviation ,

• in the example counter, if several pulse generators are used, e.g. E.g. 100 pulses per revolution,
• in the example bridge, if you subdivide the adjustable comparison resistance more finely, e.g. B. add resistance decades with increments of 0.1 Ω and 0.01 Ω.

This achieves a higher reading accuracy, in the two examples with 2 additional digits.
With 5 decimal places, the relative quantization deviation = 1/10000… 1/99999 = 10 ⁻⁴  … 10 ⁻⁵ . Whether the overall accuracy has thus increased is at least questionable. Due to the unambiguousness of the reading, it is all too easy to forget to pay attention to the other sources of measurement errors. If every resistor in the bridge has the relative error limit of 10 ⁻³ , then the relative error limit of the result is not smaller either, and specifying 5 digits would not be justifiable. In addition, the avoidance of systematic deviations ( terminal resistance , thermal voltages ) would have to be carefully considered when setting up the measurement .

Definitions

To explain the definitions of the measurement methods

Definition of the analog measuring method from DIN 1319-2: Measurement method in which the measured value is determined by continuously processing the measurement signal.	Definition of the digital measuring method from DIN 1319-2: Measurement method in which the measured value is determined by processing the measurement signal in stages.
The decisive characteristic : At least in the ideal case, the measurement signal is a clearly reversible mapping of the measurement variable. (Contrast: with the digital measuring method, a conclusion within the width of a digit is uncertain.)	The decisive characteristic : The measurement signal is a quantized mapping of the measured variable in fixed steps. (Contrast: with the analog measurement method, the measurement signal can be adjusted as finely as desired.)

To explain the preferred ads

Display of the measured values

Scale display, numeric display

Numerical display with a scale for reading intermediate values ​​below the lowest digit increment

The dial display is preferred for measuring devices that work in analogue mode .
The numerical display is preferred for digital measuring devices .

But a misinterpretation would be:

• Scale display means analog measurement method.

Counterexample: time measurement; Station clocks work with scales, but continue to turn gradually in the minute hand.

• Numerical display means digital measuring method.

Counterexample: energy measurement; Energy meters work with numeric rollers, but continue to rotate at the last digit and have a scale display for even greater resolution.

Band display, bar display

Tape display with 51 segments

The tape display contains a number of segments (typically 5 ... 200 segments), of which an increasing number is switched on as the measured variable increases. It works digitally and combines digital technology with the advantages of a dial display. With ≥ 100 segments, the gradation is hardly noticeable and one speaks of quasi-analog . The bar display on a screen also corresponds to a scale display, whereby the length of the bar can be so finely graduated with the number of pixels that subjectively the boundary to the continuous setting can be completely blurred.

Advantages and limitations of the scoreboard

Dial display	Numeric display
display
With the analog measurement method, the display can only be estimated in its subtleties.	With the digital measuring method, the display can be clearly read.
The resolution is limited
thanks to the readability to 1/2… 1/10 scale division 1… 0.1% of the final value. ${\displaystyle {\widehat {=}}}$	by grading to 1 digit step ≤0.1% of the final value with at least three-digit display.
Visual operational monitoring
is possible at a glance .	requires conscious reading and evaluating the number.
If the measured variable fluctuates rapidly
(quickly in relation to the setting or recording time)
a medium size can be read.	the indicator is unsuitable.
Trend observation or fault detection
is based curve (by Schreiber or screen) clearly easy.	is tedious using columns of numbers (using a printer or screen).

Coding

Coding is the representation of a message in an arbitrarily chosen form. Different codings are appropriate depending on the circumstances.

Reticle for incremental measuring

Counting code

Representation by a sequence of equivalent characters (pulses); with each impulse is to be counted further by one digit.
In the case of non-electrical measured variables, pulses can be generated by optical scanning (e.g. on a reticle) or inductive scanning (e.g. on a gearwheel).

Total number

The number of pulses represents the number to be coded itself. ${\displaystyle N}$

Examples:

• Checklist
• Number of revolutions of a shaft or, if there are many pulses per revolution, its positioning.
• Volume measurement with oval gear meters or turbine meters .

Oval gear meter: With every half revolution, a "volume quantum" flows through above and below.

Time-limited counting

The number of pulses in a period represents the number to be coded . ${\displaystyle \Delta N}$ ${\displaystyle \Delta t}$ ${\displaystyle n}$

${\displaystyle {\frac {\Delta N}{\Delta t}}=n\cdot z}$

with = allocation factor, e.g. B. Number of pulses per revolution if stands for the speed. ${\displaystyle z}$ ${\displaystyle n}$

Examples:

• Frequency (frequency) measurement
• Speed ​​measurement
• Flow measurement

With its countability, a frequency signal has significant advantages of a digital signal , although the frequency is clearly an analog signal due to its constant variability .

If the variable to be measured is to be determined as a frequency-proportional variable by counting, the duration of the counting must be limited.

Counting is suitable for various measuring tasks:

• using the oval gear meter as an example:

• Volume measurement for sales (delivery quantity),
• Flow measurement for operation (delivery rate or flow velocity).

Depending on the task, the total duration of the loading (which is not important in the end) must be counted or limited according to the time interval.

• using the example of induction loops in the roadway to the football stadium:
  • Unlimited count for the utilization of the parking space,
  • Temporary count for road performance.

Position code

Representation by a sequence of characters that have to be evaluated differently depending on their position in a compound.

Decimal representation

Each digit has the significance or the weighting factor of a power of ten.

Example: Decimal number 145 = 5⋅10 ⁰ + 4⋅10 ¹ + 1⋅10 ²

Angle encoder with 9 binary digits

The sub-representation of the decimal digits is

• mechanically no problem, for example with
  • Decade resistors ,
  • Digit rollers ,
• electronically difficult.

Binary or dual representation

In the simplest case, which also occurs frequently, each digit has the significance or the weighting factor of a power of two.

Example: binary number / binary number 10010001 = 2 ⁰ + 2 ⁴ + 2 ⁷ = 1 + 16 ₁₀ + 128 ₁₀ = 145 ₁₀

In the case of non-electrical measured quantities, binary digits can be represented using code disks or code rulers, which have as many paths as there are places.

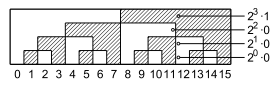
Example: angle encoder

In the picture, the binary number 111010101  330 ° is scanned with 9 sensors along the drawn radius from the inside to the outside  , if light   0 and dark   1 are evaluated. ${\displaystyle {\widehat {=}}}$ ${\displaystyle {\widehat {=}}}$ ${\displaystyle {\widehat {=}}}$

Four-lane code ruler with problem of scanning error

Due to imperfections in the adjustment, errors occur in the scanning. In the example of a code ruler shown, an 8 is read between 11 and 12 if unshaded   0 and hatched   1 are evaluated. This mistake can be avoided ${\displaystyle {\widehat {=}}}$ ${\displaystyle {\widehat {=}}}$

• by double scanning,
• by scanning a narrow synchronization field in the middle of the field of the finest gradation,
• by using a one-step code ( Gray code in the picture ), in which a value only changes on one track with each transition ; Disadvantage: no significance on the tracks. For information on the evaluation logic and code converter, see the section "Blocks of binary technology" below. ${\displaystyle N\leftrightarrow N+1}$

Avoidance of scanning errors through double scanning

Avoiding the scanning error by using one-step code

A selection of possible four-bit codes

In the case of internal binary representation, it is necessary to recode to a decimal number in order to display measured values ​​to the observing person. To do this, the device must be able to calculate (divide), or it uses the following mixed form of decimal and binary.

BCD representation

Each decimal place is individually binary coded with a BCD code . The minimum effort is 4 binary digits per decimal digit. Since only 10 of the 16 possible bit combinations are needed, there are several common codes. The 8-4-2-1 code maintains significance; on the other hand, the excess 3 code avoids the combinations 0000 and 1111, which can easily occur in the event of errors.

Example in preferred 8-4-2-1 code: 145 ₁₀ = 0001 0100 0101.

Bus coupling

In automation technology there are a number of " field buses ", e.g. B. Profibus , Interbus , EtherCAT , where the representation of the binary characters, the time sequence, the structure of a telegram, the data backup and much more are defined. However, this cannot be dealt with here.

Device technology

Preliminary remarks

A section of the electronics is inserted beforehand. It restricts itself to what is absolutely necessary to help you understand the sections that follow.

Operational amplifier

Circuit symbol of the operational amplifier; left two inputs, right one output.
Auxiliary connections, e.g. B. for supply are generally not shown

The operational amplifier is simply the workhorse of analog electronics, as it can be used for a wide variety of tasks, depending on the circuitry with passive components. The key formula for his behavior is

${\displaystyle U_{a}=V_{0}\cdot U_{d}}$

with = open circuit voltage gain. Almost always the best permissible approximations lead to the "ideal operational amplifier": ${\displaystyle V_{0}}$

${\displaystyle V_{0}\rightarrow \infty \quad ;\quad I_{P}\ ,\ I_{N}\rightarrow 0}$

Use without feedback as a comparator

Without feedback , the output has no effect on the input.

${\displaystyle U_{a}}$ can only have two values:

• positive overdriven
• negatively overdriven.

Use with feedback to the inverting input

Current-voltage converter

In the drawing, the inverting input is marked with a minus sign.

The circuit can be operated using analog technology without overdriving. This must be set because the output is not overdriven . ${\displaystyle V_{0}\rightarrow \infty }$ ${\displaystyle U_{d}\rightarrow 0}$

• Current-voltage converter

A current-voltage converter is created with ohmic feedback. Because of this , the entire input current flows through the feedback resistor. With a positive input current, the amplifier generates a negative output voltage just large enough that becomes. This applies ${\displaystyle I_{N}=0}$ ${\displaystyle I_{e}}$ ${\displaystyle U_{a}}$ ${\displaystyle U_{d}=0}$

${\displaystyle U_{a}=-\,I_{e}\cdot R_{r}\ .}$

Integrator, circuit and voltage-time diagram for = const> 0 ${\displaystyle U_{e}}$

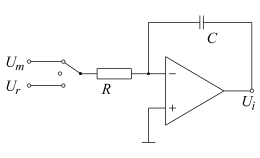
• Integrator

An integrator is created through capacitive feedback.

If the voltage is switched to the input at the time , and ${\displaystyle t_{0}}$ ${\displaystyle U_{e}}$

if the voltage is present at the output at the time , ${\displaystyle t_{0}}$ ${\displaystyle U_{a}=U_{0}}$

then is for ${\displaystyle t>t_{0}}$

${\displaystyle U_{a}(t)=U_{0}-{\frac {1}{RC}}\int \limits _{t_{0}}^{t}U_{e}(t)\mathrm {d} t}$

If = const ${\displaystyle U_{e}}$

${\displaystyle U_{a}(t)=U_{0}-{\frac {U_{e}}{RC}}(t-t_{0})}$

This results in a straight line with the rise ${\displaystyle -\,U_{e}/(RC)\,.}$

Building blocks of binary technology

See also logic gate , flip-flop

Some elementary binary building blocks

counter

Counter made of T-flip-flops for one decimal place in BCD representation

Signal-time curve for the above circuit (each flip-flop reacts to falling edge)

Counters are stored; they have a number of stable states. Each impulse changes the memory content by one digit.

With limited counting, counters work with averaging over the duration of the count.

Mechanical counters have storage elements with ten stable states.
Electronic meters have storage elements with two stable states. In decimal counters, a memory element is made up of four toggle elements.

For counting over several decimal places, the carry output Ü in the circuit diagram shown can be connected to the clock input T of another counting stage for the next higher place.

Counter structure and additional equipment

Counter with additional equipment

The four-digit decimal counter shown has a few additional features:

goal

Counting pulses only reach the counter as long as there is a 1 at the lower input.

Provision

This allows the counter to be set to 0.

prefix

If all decimal places match the preselection setting, a preselection message is output. This can be used to control other events, e.g. B.

• Stop counting,
• Reset counter and continue counting from 0.

There are also up / down counters. These contain a further control input for the counting direction and require a message about the direction of a change. Such counters are used, for example

• for position measurement using an incremental encoder , if both directions of movement are permitted,
• when measuring the voltage using a follow-up converter when the voltage rises or falls.

Counter applications

In a slightly different circuit, the counter input Z and the start-stop input S react to the transition from 1 to 0 of the input signal. Various applications are explained using the table. Then some additions follow.

Various measuring functions and auxiliary functions using counters

Timing

Example with the assumption of a reference frequency = 1 kHz with a period duration = 1 ms: ${\displaystyle f_{r}}$ ${\displaystyle T_{r}}$

Pulses were counted between start and stop . Then  ms have passed between start and stop . ${\displaystyle N}$ ${\displaystyle N}$

Frequency divider

Frequency divider for a frequency to be measured ${\displaystyle f_{m}}$

Example with 5 decimal places:

At the carry output Ü reduction ratio 100,000: 1.

Example with a number that can be set on preselection switches and with automatic reset: ${\displaystyle b}$

At the pre-selection output V reduction  : 1. ${\displaystyle b}$

Timer

Timers using reference frequency with the same assumptions as before: ${\displaystyle f_{r}}$

A pulse appears at Ü every 100 s.

A pulse appears at V every  ms. ${\displaystyle b}$

Period duration measurement

If the measurement results in a counter reading that is too small, the counting time must be extended with an auxiliary counter for . ${\displaystyle f_{m}}$

Example: With = 1 kHz and = 50 Hz, the counter reading is 20 ± 1, ${\displaystyle f_{r}}$ ${\displaystyle f_{m}}$

With a pre-coater for 1000: 1, the counter reading is 20,000 ± 1. ${\displaystyle f_{m}}$

Note: A coaster 4000: 1 with a numerator result of 80,000 ± 1 would further reduce the relative measurement uncertainty, but is not appropriate. The conversion of the display to the measured value usually only takes place in whole powers of ten (no numerical calculation, only decimal point shift);

in the example: counter reading 20,000 results in = 20,000 ms. ${\displaystyle T_{m}}$

Frequency ratio measurement

Application example: fuel consumption measurement in vehicles

The not directly measurable quantity (in l / 100 km) can be calculated by dividing by . Since both quantities can easily be represented by frequency-proportional signals, ${\displaystyle \Delta V/\Delta s}$
${\displaystyle \Delta V/\Delta t}$ ${\displaystyle \Delta s/\Delta t}$

${\displaystyle f_{m1}\sim {\frac {\Delta V}{\Delta t}}}$(Flow) and (speed) ${\displaystyle f_{m2}\sim {\frac {\Delta s}{\Delta t}}}$

division is possible by forming the frequency ratio.

Universal counter

The variety shown in the table above can be implemented in a single device. This is needed

1. Counter for the value to be displayed,
2. Counter as auxiliary coaster,
3. Precision frequency generator ( quartz crystal ),
4. Switch to different combinations of the assemblies.

Error limits using the example of time measurement

Guarantee error limits

Crystals have deviations in their frequency

• typical (even possible for consumer goods) <10 ⁻⁵ , ${\displaystyle \left|{\frac {\Delta f_{r}}{f_{r}}}\right|}$
• with greater effort (e.g. thermostatting in the quartz furnace ) <10 ^{−8 can be achieved} ,
• Atomic clock frequency standards (e.g. rubidium oscillator ) create <10 ⁻¹¹ .

For counters over 5 decades ( i.e. count <10 ⁵ ) using a quartz time base, the reference frequency applies due to these typical error limits ${\displaystyle N}$ ${\displaystyle f_{r}}$

${\displaystyle \left|{\frac {\Delta f_{r}}{f_{r}}}\right|=\left|{\frac {\Delta N}{N}}\right|<10^{-5}\quad ;\quad |\Delta N|<10^{-5}\cdot N<1\ .}$

The effort with regard to the error limits of the quartz is optimally chosen for the given meter; it is not worthwhile to push the guarantee error limits below a quantization step.

Measurement uncertainty

For the measurement uncertainty due to counting, the example of a time to be measured applies

${\displaystyle t_{m}=N_{m}\cdot t_{r}-t_{3}+t_{4}=N_{m}\cdot t_{r}+t_{1}-t_{2}=t_{r}\cdot (N_{m}+\Delta N)\ .}$

For the quantization or digitization deviation in time measurement

The digitally displayed time differs from the correct time by the measurement error

${\displaystyle F=t_{2}-t_{1}=t_{3}-t_{4}\ .}$

Since this difference can be positive or negative, but the amount remains smaller than , the known fact applies ${\displaystyle t_{r}}$

${\displaystyle \;-1<\Delta N<+1\ .}$

Time measurement deviation during synchronization

If it succeeds in special cases,

• to synchronize the clock with the beginning of the process to be measured or
• start the process synchronously with the clock,

this halves the width of the possible deviation, and depending on the version, this is between

    ${\displaystyle \,0<\Delta N<+1}$

and

${\displaystyle \,-1<\Delta N<0\ .}$

You can see this in the next picture with narrow pulses - depending on whether the circuit reacts to falling or rising edges.

With a frequency reduction from a continuous clock, there is synchronization both at the beginning and at the end of the generated period, so that the frequency ratio is always exact.

Digital-to-analog converter (DAU)

DAU in measurement technology

There are only a few physical quantities for which a quantization is known. Since even this quantized nature is practically not recognizable, there is no need for a DAC as a measuring device. (Who measures an electric current by counting electrons, except when it is below 10 ⁻¹⁶  A?) Since the DAU is part of some measuring devices and simply a counterpart to the ADC, it will be dealt with here.

Strictly speaking, a digital-to-analog converter is something nonsensical: something stepped cannot be turned into something stepless. Rather, the DAU should be understood as follows: It converts digitally coded information into a form that an analog device can understand.

Representative designs

Of the numerous developments, three are explained here.

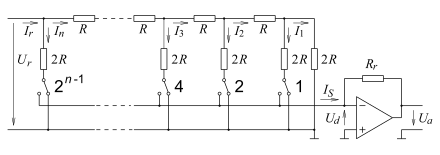
DAU with weighted resistances

Circuit to DAU with voltage summing

The circuit shows a DAC with voltage summing by weighted resistors in BCD representation. Here the voltage is created by specifying two decimal digits in 8-4-2-1 code and the reference voltage . ${\displaystyle U_{a}}$ ${\displaystyle U_{r}}$

${\displaystyle U_{a}}$can be set by opening switches between 0 and 99% of in increments of 1%. If necessary for a finer resolution, further decades can be added, as long as this is responsible for the quality of the resistors and switches. (Because undesirable properties of switches and resistors sometimes influence the inaccuracy of the output variable.) ${\displaystyle I\cdot R}$

${\displaystyle I=-\,U_{r}/R_{r}\ ,}$

because of ( virtual mass ); regardless of the switch positions. ${\displaystyle U_{d}=0}$

Each binary one of the binary coded -digit decimal number opens the associated switch and thus the relevant resistor is looped into the chain of resistors. ${\displaystyle n}$

${\displaystyle U_{a}=I\cdot \sum R_{\text{ein}}=-{\frac {\mathrm {Dezimalzahl} }{10^{n}}}\cdot U_{r}\cdot {\frac {R}{R_{r}}}\ .}$

DAU with resistance chain ladder

Circuit to DAU with current summation

The circuit shows a DAC with current summation through resistor chain conductors ( R-2R network ) in binary representation. There are only two resistance values regardless of the significance of the respective digit. The voltage is created here by specifying binary digits. ${\displaystyle U_{a}}$ ${\displaystyle n}$

${\displaystyle I_{i}=2^{i-1}\cdot I_{1}}$

for . ${\displaystyle i=1\,\ldots \,n}$

${\displaystyle I_{r}=U_{r}/R=2\cdot I_{n}=2^{n}\cdot I_{1}}$ .

Each one of the binary number places the associated switch to the left, and the current flowing through it is switched to the busbar from . This total current flows on through the feedback resistor to the output of the operational amplifier. ${\displaystyle I_{S}}$ ${\displaystyle R_{r}}$

${\displaystyle I_{S}=\sum _{i}I_{i\;{\text{ein}}}=I_{1}\cdot \mathrm {Bin{\ddot {a}}rzahl} }$

${\displaystyle U_{a}=-I_{S}\cdot R_{r}=-{\frac {\mathrm {Bin{\ddot {a}}rzahl} }{\displaystyle 2^{n}}}\cdot U_{r}\cdot {\frac {R_{r}}{R}}\ .}$

General: are required for the two versions shown so far

1. Precision voltage source,
2. Precision resistors,
3. Semiconductor switches that block or conduct as ideally as possible.

DAU with pulse width modulation

Circuit to DAC with pulse width modulation

The circuit shows a DAC with pulse width modulation . Here the voltage is created by specifying a number for the duty cycle of a square-wave voltage . ${\displaystyle U_{a}}$

Time course for pulse width modulation

A counter that is initially set to zero records a clock frequency and compares its counter reading with two pre-selected numbers. When the first number is reached (after a period of time ) an SR flip-flop is set to A = 1. When the second number is reached (after a certain period of time ) the flip-flop is set to A = 0 and the counter is also reset to zero. As long as A = 0, a reference voltage is applied to a low-pass filter or a mean value image; zero potential is applied for the remainder of the period. The arithmetic mean of this voltage is ${\displaystyle f_{r}}$ ${\displaystyle N_{1}}$ ${\displaystyle t_{1}}$ ${\displaystyle N_{2}}$ ${\displaystyle t_{2}}$ ${\displaystyle U_{r}}$

${\displaystyle U_{a}={\frac {t_{1}}{t_{2}}}U_{r}={\frac {N_{1}}{N_{2}}}U_{r}\ .}$

The advantage of this circuit is the lack of precision resistors and many switches, the disadvantage is its slow response due to the low pass.

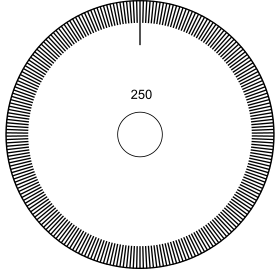
With you determine the fineness of the graduation and the period duration. With you set the tension, where is. If the smallest step size is allowed to be 0.4% of the final value, then  ≈ 250 is selected, for which an 8-bit counter is sufficient. At = 1 MHz = ¼ ms is required for this . Microprocessor circuits offer counters with 16 bits; This means that the resolution is much finer, but then in the maximum case = 65 ms, and the response time is ≫ 200 ms, depending on the smoothing requirements. ${\displaystyle N_{2}}$ ${\displaystyle t_{2}}$ ${\displaystyle N_{1}}$ ${\displaystyle U_{a}\sim N_{1}}$ ${\displaystyle N_{2}}$ ${\displaystyle f_{r}}$ ${\displaystyle t_{2}}$ ${\displaystyle t_{2}}$

Analog-to-digital converter (ADC)

Measuring devices for process variables

Various analog-digital converters have already been dealt with in the previous sections

• Frequency measurement (speed, flow measurement)
• Volume measurement
• Angle and length measurement
  • incremental process with a graticule
  • absolute procedure with code disk,
• Timing.

Electrical voltage meters

Execution types

Depending on the measuring task, there is a wide range of devices to choose from according to the following criteria:

Measured value output
with computer connection	with display
Measured value display and resolution
in pure binary code with 8… 14 (… 28) digits	in BCD format with 2000… 100,000 points or "3½-digit"… 5-digit (… 8½-)
Absolute resolution
smallest resolvable voltage: Standard devices 100 μV Top devices 1 μV ... 10 nV
Working method
Fast with instantaneous value quantization - for rapidly changing measured variables or if a larger number of measuring points is to be queried using a switch (multiplexer).	Slow with averaging (integration) - to suppress mains hum ( mains- synchronous interfering AC voltage) or interfering pulses (from switching processes).
Measurement data acquisition with multiplexer	Integration attenuates the interference. Integration over an integer multiple of the period of the interference signal completely suppresses it; the constant component or mean value contained in the voltage is retained. ${\displaystyle {\overline {U}}}$

Switching to the parallel converter

Representative designs

Of the numerous developments, four are explained here, two rapid and two integrative.

Parallel converter

The voltage to be measured is compared with all possible quantization levels at the same time. To obtain a -digit binary number one needs comparators. ${\displaystyle U_{m}}$ ${\displaystyle n}$ ${\displaystyle 2^{n}-1}$

Characteristic curve of a parallel converter. H stands for HIGH = positively overdriven, L for LOW = negatively overdriven.

For operation on the example with : ${\displaystyle n=2}$

There are four voltages formed by the voltage divider  ,  ,  , simultaneously compared. This converter, which is very roughly graded for reasons of clarity, can only deliver 4 different measured values. The fourth comparator for the highest level of the characteristic provides a fifth value: Exceeding the measuring range . ${\displaystyle U_{r}}$ ${\displaystyle {\frac {3}{4}}U_{r}}$ ${\displaystyle {\frac {1}{2}}U_{r}}$ ${\displaystyle {\frac {1}{4}}U_{r}}$ ${\displaystyle U_{m}}$

Parallel converters are extremely fast ("flash converters") and extremely complex. Versions with ≥ 6 bits work in the top class with a conversion time ≤ 1 ns (conversion rate ≥ 1 GHz). Integrated converters with 10 bits (1023 comparators) are also on the market.

The pipeline converters are a further development . They are made up of several independent stages in a pipeline architecture . Their stages usually consist of parallel converters over a few bits. A rough quantization is carried out in each pipeline stage, this value is converted into an analog signal with a DAC and subtracted from the buffered input signal. The residual value is amplified and passed on to the next stage. The advantages lie in the greatly reduced number of comparators (60 for four four-bit converter stages) and in the higher possible resolution of up to 16 bits. The latency time increases with each step , but the sampling rate only decreases because of the longer settling time with higher resolution.

Serial converter

Circuit to the serial converter

The voltage to be measured is compared with a voltage generated at the DAC . One after the other is changed in several steps and approximated as closely as possible. There are several strategies for doing this; here the successive approximation with the weighing or compensation method is explained. ${\displaystyle U_{m}}$ ${\displaystyle U_{v}}$ ${\displaystyle U_{v}}$ ${\displaystyle U_{m}}$

Time course for the successive approximation (for example according to the text)

for operation

Adoption:	${\displaystyle U_{m}}$> 0 and > 0 ${\displaystyle U_{v}}$
Step 1a:	A comparison voltage is generated by setting the most significant bit to 1 and all others to 0. ${\displaystyle U_{v}}$
Step 1b:	If so, the bit is reset to 0. ${\displaystyle U_{v}>U_{m}}$ If so , then the bit is left at 1. ${\displaystyle U_{v}<U_{m}}$
Step 2a:	A 1 on the next least significant bit is added.
Step 2b:	Like step 1b
etc

To obtain a -digit binary number one needs comparisons. Finally is  . This is the smallest voltage jump that can be set on the DAU. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle U_{m}-U_{v}<U_{q}}$ ${\displaystyle U_{q}}$

Example of this:

4-bit DAC with = 1 V at = 6.5 V. ${\displaystyle U_{q}}$ ${\displaystyle U_{m}}$

According to the signal-time diagram, the measured value = 0110 _B ⋅ = 6 V. ${\displaystyle U_{q}}$

The input signal of the DAU set at the end is regarded as the result of the ADC (binary or BCD graded).

Measurement of instantaneous values; however, must not change during the setting of . A sample-and-hold circuit is often used for this, which temporarily stores analog data during the conversion. Typical conversion time 1… 100 μs. ${\displaystyle U_{m}}$ ${\displaystyle U_{v}}$ ${\displaystyle U_{m}}$

ADU with the intermediate size of time

Switching to the two-ramp procedure

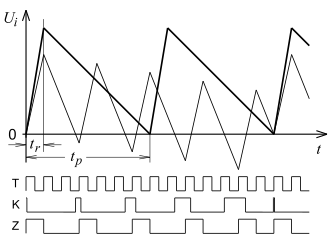
The process is explained using the two-ramp or dual-slope process.

The voltage to be measured charges the capacitor of an integrator for a limited period of time (see above in the section on operational amplifiers ). The capacitor is then discharged again in a controlled manner. Both processes run ramp-shaped ( linear ) with DC voltage plotted over time . ${\displaystyle U_{m}}$

for operation

Adoption:	${\displaystyle U_{m}>0}$ ; then ${\displaystyle U_{r}<0}$
Start:	at with ${\displaystyle t=0}$ ${\displaystyle U_{i}=0}$
Step 1:	Integration (charging of the capacitor) with for a fixed duration, e.g. B. = 20 ms. ${\displaystyle U_{m}}$ ${\displaystyle t_{i}}$ ${\displaystyle U_{i}(t_{i})=-{\frac {1}{RC}}\int \limits _{0}^{t_{i}}U_{m}\mathrm {d} t=-{\frac {t_{i}}{RC}}U_{m\;{\text{gemit}}}}$
Step 2:	Downintegration with a fixed end value . ${\displaystyle U_{r}}$ ${\displaystyle U_{i}=0}$ ${\displaystyle U_{i}(t_{i}+t_{m})=0}$ ${\displaystyle =-{\frac {t_{i}}{RC}}\ U_{m\;{\text{gemit}}}-{\frac {1}{RC}}\int \limits _{t_{i}}^{t_{i}+t_{m}}U_{r}\mathrm {d} t}$ ${\displaystyle {\frac {t_{i}}{RC}}U_{m\;{\text{gemit}}}=-{\frac {1}{RC}}U_{r}\cdot t_{m}}$ ${\displaystyle U_{m\;{\text{gemit}}}=-U_{r}{\frac {t_{m}}{t_{i}}}\;;\ U_{m\;{\text{gemit}}}\sim t_{m}}$ (Intermediate size)

Temporal course of the two-ramp procedure

Both times are determined by counting. Is shown

${\displaystyle N_{m}=f_{r}\cdot t_{m}\quad }$.

Is used for the integration period

${\displaystyle N_{i}=f_{r}\cdot t_{i}\quad }$.

${\displaystyle U_{m\ {\text{gemit}}}=-U_{r}{\frac {N_{m}}{N_{i}}}\ ,}$regardless of . ${\displaystyle R{\text{, }}C{\text{, }}f_{r}}$

${\displaystyle N_{m}}$stands for the value of the voltage to be measured averaged over the duration of the integration; effective interference suppression of 50 Hz signals if ; with , integer. Then ${\displaystyle t_{i}={\frac {k}{50\;\mathrm {Hz} }}=k\cdot 20\;\mathrm {ms} }$ ${\displaystyle k>0}$ ${\displaystyle U_{m\ {\text{gemit}}}={\overline {U_{m}}}\ .}$

Typical integration time 1… 300 ms. Devices with offer good suppression of network coupling worldwide, both in 50 Hz and 60 Hz networks. ${\displaystyle t_{i}=k\cdot {\text{ 100 ms}}}$

ADU with the intermediate size frequency

Circuit for the charge balance method

The process is explained using the charge balance or charge balancing process.

The voltage to be measured charges the capacitor in an integrator. It is constantly discharged again by short current surges in the opposite direction; on average, the charge balance is balanced. ${\displaystyle U_{m}}$

for operation

Temporal progression in the charge balance method

Adoption:	${\displaystyle U_{m}>0}$ ; then ${\displaystyle U_{r}<0}$
further:	${\displaystyle -I_{r}}$ > 2 ⋅ maximum value of ${\displaystyle I_{m}}$
Start:	at with ${\displaystyle t=0}$ ${\displaystyle U_{i}=0}$
Step 1:	Loading with for a fixed short duration , ${\displaystyle I_{m}+I_{r}<0}$ ${\displaystyle t_{r}}$ where ≪ 20 ms ${\displaystyle t_{r}=1/f_{r}}$
Step 2:	Unloading with a fixed end value ${\displaystyle I_{m}>0}$ ${\displaystyle U_{i}=0}$
Step 3:	like step 1
etc

The upper part of the signal-time diagram shows the voltage at the output of the integrator for a DC voltage to be measured  . The charge balance is balanced along the thicker sawtooth line after a period. ${\displaystyle U_{i}}$ ${\displaystyle U_{m}}$

${\displaystyle \int \limits _{0}^{t_{p}}I_{C}\mathrm {d} t=0=t_{r}\cdot (I_{m}+I_{r})+(t_{p}-t_{r})\cdot I_{m}}$

${\displaystyle I_{m}=-I_{r}{\frac {t_{r}}{t_{p}}}{\text{ ;}}\quad I_{m}\sim {\frac {1}{t_{p}}}=f_{m}}$     (Intermediate size)

The measurement of leads by counting for the duration on the counter reading that is displayed. ${\displaystyle f_{m}}$ ${\displaystyle t_{i}}$ ${\displaystyle N_{m}}$

As a timer for the frequency is counted up to the count  ;     ${\displaystyle t_{i}}$ ${\displaystyle f_{r}}$ ${\displaystyle N_{i}}$ ${\displaystyle t_{i}=N_{i}\cdot t_{r}}$

The order of magnitude: = a few 100 ms. ${\displaystyle t_{i}}$

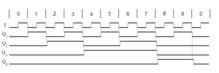
The thinner sawtooth line in the picture differs from the thicker one in two ways:

• The voltage is greater by a factor of 5/2 and generates a number of charging cycles that is greater by the same factor. ${\displaystyle U_{m}}$
• The message from the comparator does not start the timer immediately.

In the circuit shown here, the timing element precisely generates the duration from one rising edge to the next. This synchronization of the timing element to the clock frequency not only runs to the zero line, but continues until the point in time of synchronization. The associated deviation, however, is less than a digit increment - over an arbitrarily long counting period. The three square wave signals in the picture explain the process for the course of the thinner line of ${\displaystyle t_{r}}$ ${\displaystyle f_{r}}$ ${\displaystyle U_{i}}$ ${\displaystyle U_{i}}$

• upper signal for the T akt (So ), ${\displaystyle f_{r}}$
• average signal for the output of the K omparators,
• lower signal for the output of the Z eitgliedes.

The current flows continuously during the counting period . In addition, the current is switched on briefly so that the capacitor does not charge on average. ${\displaystyle t_{i}}$ ${\displaystyle I_{m}}$ ${\displaystyle N_{m}}$ ${\displaystyle I_{r}}$

${\displaystyle \int \limits _{0}^{t_{i}}I_{C}\mathrm {d} t=0=\int \limits _{0}^{t_{i}}I_{m}\mathrm {d} t+I_{r}\cdot t_{r}\cdot N_{m}}$ ${\displaystyle ;\quad I_{m\;{\text{gemit}}}\cdot t_{i}=-I_{r}\cdot t_{r}\cdot N_{m}}$

${\displaystyle U_{m\;{\text{gemit}}}=R_{m}I_{m\;{\text{gemit}}}=-R_{m}I_{r}{\frac {N_{m}}{N_{i}}}=-U_{r}{\frac {R_{m}}{R_{r}}}{\frac {N_{m}}{N_{i}}}\ ,}$only dependent on the reference voltage and a resistance ratio, regardless of  . ${\displaystyle C{\text{ und }}f_{r}}$

In terms of its metrological quality, this procedure is similar to the two-ramp procedure, but is still somewhat superior to it (it is switched on continuously). ${\displaystyle U_{m}}$

Measurement errors

For measurement deviations that are solely due to the imperfection of the digital voltage measuring device, the manufacturer usually specifies error limits . These are made up of two parts,

• resulting from the comparison value (and possibly other multiplicative causes included in the result) and
• resulting from zero point and digitization (and possibly other additional causes).

Interference voltages in digital multimeters

For examples of correct information and use, see Measuring device deviation and digital multimeter .

Important influencing variables that can cause measurement errors and that are not included in the device error limits come into question

• Current consumption of the input terminals,

as well as due to the properties of the applied voltage

• Frequency,
• Curve shape,
• superimposed interference voltage,
  • Series interference voltage, which can be suppressed in integrating processes z. B. by a factor of 10 ⁻³ at 50 and 60 Hz,
  • Common-mode interference voltage that can be suppressed in integrating processes, e.g. B. by a factor of 10 ⁻⁵ at 0… 10 kHz.

Individual evidence

1. ↑ DIN 1319-1, Fundamentals of measurement technology - Part 1: Basic terms . 1995
2. ↑ DIN EN ISO 80000-3: 2013-08 Sizes and units - space and time , No. 3-15
3. ↑ DIN 1319-2, Basics of measuring technology - Part 2: Terms for measuring equipment . 2005
4. ↑ Tutorial Precision Frequency Generation Utilizing OCXO and Rubidium Atomic Standards with Applications for Commercial, Space, Military, and Challenging Environments IEEE Long Island Chapter March 18, 2004 (PDF; 4.2 MB) Retrieved June 7, 2012.