Place value system
A priority system , positioning system or polyadisches Number System is a number system , in which the ( additive ) value of a symbol from its position, the location dependent. For example, in the widely used decimal system, the number “1” has the value 1 · 100 for the example value “127”, the value 2 · 10 is added for the number “2” and 7 · 1 - the symbols for the “7” "1", "2" and "7" have a value that depends on where they are in the number. Assuming a finite supply of symbols (usually called digits or numerals , in the example "0" .. "9"), the number of required digits depends logarithmically on the size of the number shown - in contrast to addition systems , which have this relationship ( asymptotically , i.e. for very large numbers) is linear .
The size of the number supply plays a decisive role. In the decimal system example, the number range is “0” to “9”, these are different symbols. In the important integral systems, the value of the number shown is equal to the sum of the products of each digit value with its value , so a polynomial in the values of the numbers as coefficients ; in the example: numerical value = "1" · 10 2 + "2" · 10 1 + "7" · 10 0 . Therefore, as a base or base number of the system, respectively. The representation of numbers with reference to a base is often called their -adic representation (not to be confused with -adic numbers ). Any whole number is suitable as a basis for a place value system.
Examples of positional notation are the commonly used in everyday life decimal ( dek adisches system with the base 10), which is often used in the data processing Dual System ( dy adisches system with base 2), the octal (base 8), the hexadecimal system (with base 16) and the sexagesimal system (base 60). An example of a number system that is not a place value system is that of Roman numerals . It is an addition system.
history
The system originally comes from India. With his works, Adam Ries spread written arithmetic using the place value system in German-speaking countries.
Basic concepts
In a place value system, numbers are represented with the help of digits and possibly signs or separators . The value of a number results from the arrangement of the digits from their numerical values and place values.
Base
The total number of digits is called the basis of the place value system. A place value system with the base is also called -adic number system . The most common bases are:
- : the dual system used in digital technology
- : our familiar decimal system
- : the hexadecimal system important in data processing .
For further -adic number systems used in practice, see the section Common bases .
Stock of digits
In a place value system, a number system with exactly different numbers is used. In the most common digit systems, a digit of the type given below stands for an integer value . When counting up (this corresponds to the addition of a one), the sequence proceeds to the digit with the next higher value; with the few available digits only a few counting steps would be possible. Therefore, in the case of the most significant digit, a one is added to the lowest digit and a one is added to the next highest digit. In the event of a transfer to an unoccupied position, this is pre-filled with a zero; in the case of an unlimited number of digits, this means that counting can be continued indefinitely.
In the common number systems, the following digits are used and assigned a digit value (for better differentiation, digit symbols are printed in bold and their associated values are printed normally):
- In the dual system, the two digits 0 and 1 are used and the values of the numbers 0 and 1 are assigned to them.
- In the decimal system, the ten digits 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 and 9 are used and the values of the numbers from 0 to 9 are assigned to them in the conventional order.
- In the hexadecimal system, the sixteen digits 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , A , B , C , D , E and F are used and the values of the decimal numbers from 0 to 15 are assigned to them .
If the base is very large, there is usually a combination of a few digits in another number system. In the sexagesimal system it is common to use a decimal number from 0 to 59 as a "digit" instead of 60 different characters. IP addresses in IPv4 format consist of 4 "digits" that can have values from 0 to 255 and are separated by a period, for example 192.0.2.42. Another way of assigning digit to digit value was chosen for the Base64 encoding .
Sometimes other symbols are used instead of numbers; For example, in electronics the two states of a dual system are often not described as 0 and 1 , but instead h and l (for "high" and "low" voltage values) are used (rarely o and l for "on" and " low ").
Place and significance
The value of a number results from the arrangement of the digits in a digit sequence. Every place that a digit occupies or is intended to occupy in this arrangement is a place . Each digit is assigned a value that corresponds to a power of the base. The position with the lowest value is on the far right. In the decimal system, for example, when representing natural numbers:
- The value of the first digit from the right ("units digit") is .
- The value of the second digit from the right ("tens digit") is .
- The position of the third digit from the right (“hundreds”) is , and so on.
It proves to be advantageous here to number the digits not from one but from zero. In this way, the th position then has just the value . Negative exponents are also allowed when representing rational numbers.
Representations of different types of numbers
Representation of natural numbers
Natural numbers are represented in the -adic representation by a finite sequence of digits in the form
shown. This sequence of digits now becomes the number
assigned, where is the digit value assigned to the digit.
It can be shown that for every natural number there is a sequence of digits whose assigned value is. In general there are even several episodes. It is sufficient to put the number 0 = 0 in front of higher-value places as often as you like . If sequences with a leading 0 are forbidden, it can be shown that this assignment is even one-to-one , that is, for every natural number there is exactly one sequence whose assigned value is. As an exception to this prohibition, the number 0 is not assigned the empty sequence (i.e. the sequence without a single term), but the sequence with exactly one digit, namely the one to which the value 0 is assigned (i.e. 0 ) around this number to make typographically recognizable.
As an example of the number representation given, consider the sequence of digits 694 in the decimal system ( ). It stands for:
The sequence of digits 2B6 in the hexadecimal system ( ) stands for with = 6 = 6; = B = 11; = 2 = 2.
So the sequence 2B6 has the value of the decimal number
Accordingly, the sequence of digits 1010110110 in the dual system ( ) has the value of the decimal number
Representation of whole numbers
In a system consisting of a positive base and a purely non-negative set of digits, negative numbers cannot be represented. A minus sign (" - ") is added to such systems , which may precede the number constants. This goes hand in hand with a slight loss of uniqueness, since the number 0 can be written as a signed zero in the form +0, –0 or ± 0. Representations of numbers other than 0 that are not preceded by a minus sign are interpreted as positive numbers. Sometimes, however, you want to emphasize this positivity (e.g. if the number is to be identified as an increment ). In such cases, a plus sign (“ + ”) is placed in front of the display .
Representation of rational numbers
The notation is expanded into the negative exponents of the base by adding the corresponding places to the right of a separator added for this purpose in a seamless sequence. In German-speaking countries (with the exception of Switzerland), this is the comma " , ", in English-speaking countries it is the point " . «Common. The values of the digits after the separator are multiplied by, whereby the position after the comma indicates. For example, the rational number 1 + 3/8 = 1.375 in the 2-adic place value system is represented by the number sequence 1.011 . Indeed it is
After adding the separator, many rational numbers can be represented -adic , but by no means all, because it can happen that an infinite sequence of decimal places is required for representation, which is then periodic . Usually this period is marked by a line drawn over the repeating digits, marking the length of the period and (finite) writing down without dots.
While the number 1/5 = 0.2 in the decimal system has the finite digit sequence 0.2 , its representation in the dual system is periodic:
- 0.00110011 ... 2 = 0, 0011 2 .
In contrast, the sequence of digits is 0.1 in 3-adic (ternary) system the rational number 1 · 3 -1 = 1/3 that in the decimal system of an infinite periodic sequence of digits 0.333 ... = , 0 3 dec corresponds.
In general, a fraction has a finite -adic representation if and only if all prime factors of its denominator are also prime factors of (at and ) after it has been reduced . (For a finite representation in the decimal system, the abbreviated denominator must therefore be a product of the numbers two and five. Exactly then the fraction is a decimal fraction in the narrower sense or becomes one by expanding it.)
The finite representations form the ring
- ,
where stands for the set of prime factors of . With these rational numbers, the denominator only has prime divisors in a completely abbreviated fraction representation . For each non-empty the sub-ring of (as itself) lies dense both in and in , i.e. H. any real number can be approximated with arbitrary precision using numbers from .
If one only considers representations of finite length, then the digit sequences 1 , 1,0 , 1,000 in the decimal system all designate the same rational number 1 (not to mention the representations 01 , 0001 with leading zeros). These ambiguities can be suppressed by prohibiting leading and trailing zeros. If, however, the infinite representations belong to the system from the beginning, then the non-terminating representation 1,000 ... = 1, 0 and beyond that the completely different-looking representation 0.999 ... = 0, 9 (all with the value 1) are added, see the Article 0.999… .
Usually misunderstandings are not to be feared, so that both representations can be allowed. However, uniqueness is e.g. B. required for the Z-curve , which maps injectively and where two sequences of digits are pressed alternately into one. The points of discontinuity of the function are, by the way, exactly the arguments that have a finite -adic representation.
The -adic representation of a shortened fraction with and relatively prime to the base has 0 for the period length, so it is finite. Otherwise is an element of the prime remainder class such that is (with as Euler's φ-function ). The -adic period length of the shortened fraction is then the smallest exponent for which is a divisor . (See also the section Algorithm for Rational Numbers and the article Rational Number # Decimal Fraction Expansion .)
Representation of real numbers
In principle, real numbers are represented in the same way as rational numbers are represented by b -adic expansion. In the case of rational numbers, this yields a terminating or an infinite periodic sequence of digits.
The b -adic expansion of an irrational number (like π or ), on the other hand, always yields an infinite non-periodic sequence of digits. By extending the fractional part, you can approximate the irrational number as precisely as you like.
As with the rational numbers with an infinitely periodic sequence of digits, a finite representation for irrational numbers is possible by introducing new symbols, as was done here for the examples π and .
Nevertheless, not every real number can be represented as a finite string, even with any number of additional characters, but finite numbers. This is because the set of real numbers is uncountable , but the set of all finite representations with a finite set of characters can only be counted .
If, however, the "representation" of a real number is understood to mean the sequence of digits resulting from the b -adic expansion, then every real number can be represented as a (possibly infinite) b -adic fraction, even if not every such fraction can actually be written down.
Formulas
Calculation of a digit value
The last digit of the -adic representation of a natural number is the remainder of when dividing by . This rest is also through the expression
given; the Gaussian bracket denotes . More generally, the number formed by the last digits of is the remainder of when dividing by .
The numeral at the th position (from the right to the units digit starting with zero and to the left progressively counted) a positive real number is
This is an element of the standard number set . If you add negatives , for which the corresponding (negative) decimal place results, then you have
with a sufficiently large
Rational Numbers Algorithm
For rational (and a basis ) the above formula can be embedded in the following algorithm:
function b_adic(b,p,q) // b ≥ 2; 0 < p < q
static Ziffernvorrat = "0123..."; // bis zum Zeichen mit dem Wert b–1
begin
s = ""; // die zu bildende Zeichenkette
pos = 0; // hier sind alle Stellen rechts vom Komma
while not defined(occurs[p]) do
occurs[p] = pos; // die Nummer der Stelle mit dem Rest p
bp = b*p;
z = floor(bp/q); // Index z der Ziffer im Vorrat: 0 ≤ z ≤ b-1
p = bp − z*q; // p ganzzahlig: 0 ≤ p < q
if p = 0 then pl = 0; return (s); end if
s = s.substring(Ziffernvorrat, z, 1);
// Ziffer aus dem Ziffernvorrat dranhängen.
// substring(s, 0, 1) ist die erste Ziffer nach dem Komma
pos += 1;
end while
pl = pos - occurs[p]; // die Periodenlänge (0 < pl < q)
// Markiere die Ziffern der Periode mit einem Überstrich:
for i from occurs[p] to pos-1 do
substring(s, i, 1) = overline(substring(s, i, 1));
end for
return (s);
end function
The first line highlighted in yellow corresponds to the numerical calculation from the previous section.
The following line calculates the new remainder of the division modulo the denominator . The Gaussian bracket causes
floor
From this it follows and taken together
Since all remainders are thus integer non-negative and smaller than , so there are only many different of them, they must be repeated in the -loop . The return of a remainder is determined by the existence of the associative data field .
while occurs[p]
The period of the digits has the same length as the period of the remainders. (For more details on the period length, see above .)
Calculation of the number of digits
The number of digits in the -adic representation of a natural number is
Add a digit
- If you add a digit to the -adic representation of a number on the far right , you get the -adic representation of the number .
- If, on the other hand, you put the number in front of the left , you get the -adic representation of the number , where the number of digits is from , as stated above .
Common bases
- The best-known and most common place value system is the decimal system (ten system) with base 10 and the digits 0 to 9 . The decimal system originally comes from India. The Persian mathematician Muhammad ibn Musa al-Chwarizmi used it in his arithmetic book, which he wrote in the 8th century. The system was introduced in Europe as early as the 10th century, back then without a zero . However, it did not gain acceptance until the 12th century with the translation of the aforementioned arithmetic book into Latin. The BCD code is used to store decimal digits in the computer .
- In the 17th century, the mathematician Gottfried Wilhelm Leibniz introduced the dual system (binary number system) with dyadics, i.e. the place value system with the base 2 and the digits 0 and 1 . This is mainly used in information technology, as its logic is based solely on bits that are either true or false or 1 or 0.
- Since binary representations of large numbers are confusing, the hexadecimal or hexadecimal system is often used instead, which works with the base 16 (and the digits 0 , 1 ,…, 9 , A , B ,…, F ). Hexadecimal and binary representation can easily be converted into one another, since one digit of a hexadecimal number corresponds to exactly 4 digits (= 1 nibble ) of a binary number.
- In computer technology, in addition to the binary and hexadecimal system, the octal system for base 8 (digits 0 to 7 , three binary digits = one octal digit) is used. This use is decreasing, however, since the word lengths of eight bits that are customary today cannot be converted into a whole number of digits in the octal system.
- Base 64 is also used with Base64 (with an unusual symbol sequence); the base 62 at base62 with the digits 0 to 9 , A to Z and a to z ; and occasionally the base 32 with the digits 0 to 9 and a to v under the name Radix32 .
- From around 1100 BC In the Indo-Chinese region, abacus tables were used, which are based on a unary system . But see above for the unary system in blocks of five, which, however, is an addition system.
- The vigesimal system uses 20 as a base. It was probably created because the toes were also used for counting in addition to the fingers, and a. common in almost all Mesoamerican cultures. The most advanced system of this kind was used by the Maya in the Classical Period for astronomical calculations and for displaying calendar dates. It was a question of a place value system "with a jump", because in the second place only the digits from 1 to 18 appear in order to reach 360 as the third place value (approximate length of the solar year). The Maya knew zero and also used it in their calendars .
- The Indians of South America used number systems based on 4, 8 or 16 because they calculated with hands and feet, but did not include the thumbs.
- The duodecimal system is based on 12. We find it in the calculation with dozen and gros and in the Anglo-Saxon system of measurement (1 shilling = 12 pence) (see also old weights and measures ). The hour counting also originated in this system. In many polytheistic religions there were 12 main gods, e.g. B. in ancient Egypt divided into three supreme gods and 3 × 3 assigned gods. (The three was considered the perfect number; see also Trinity ).
- The Babylonians used a number system with the base 60 ( sexagesimal system ; see also History of Weights and Measures ).
- A possible number system to be expected based on base five for peoples who only use one hand for counting has not yet been discovered. In Bantu languages, however , the names of the numbers 6, 7, 8 and 9 are often foreign words or can be understood as 5 + 1, 5 + 2, 5 + 3, 5 + 4, which indicates a number system based on base 5.
- For example:
Swahili: 1 = moja, 2 = mbili, 3 = tatu, 4 = nne, 5 = tano, 6 = sita, 7 = saba, 8 = nane, 9 = kenda (Arabic: 6 = sitta, 7 = saba 'a)
Tshitschewa: 1 = modzi, 2 = wiri, 3 = tatu, 4 = nai, 5 = sanu, 6 = sanu ndi-modzi, 7 = sanu ndi-wiri, 8 = sanu ndi-tatu, 9 = sanu ndi -nai
- For example:
- The quinary system is particularly pronounced in the South American Betoya: 1 = tey, 2 = cayapa, 3 = tozumba, 4 = cajezea, 5 = teente, 10 = caya duck, 15 = tozumba duck, 20 = caesea duck.
- The Senär system is suitable for counting up to thirty-five with 2 × 5 fingers. Linguistic traces of such a system are very rare (for example Breton 18 = triouec'h , about "3 6er")
- The earlier assumption that the Maori used a base 11 system is now considered outdated. Some races use the base 18 system.
Conversions
Sometimes you need conversions between place value systems. If the decimal system is not involved, it can be used as an intermediate step. The following calculations can also be carried out with the help of a pocket calculator, where the numbers are usually only input and output in the decimal system.
In particular, when numbers are to be converted from one system to another, it is customary and expedient to identify the sequence of digits with a subscript of the base of the number system used. A missing suffix and the suffix 10 stand for the conventional decimal representation, explicitly also dec or dec . The suffixes 2 or b identify numbers represented in binary and 16 or h in hexadecimal. Furthermore, the standard rate is assumed as the set of digits . Occasionally the marked sequence of digits is put in square brackets.
There are two main variants
- the iterated Euclidean division starting at the digits of low significance, and
- the evaluation of the digit polynomial, for example in a type of Horner's scheme . The smallest number of multiplications is required when starting with the most significant digit.
The selection is best based on which procedure can be carried out most easily on the existing calculator.
Example 1: Conversion of a representation on base 10 into a representation on base 12
A number has the decimal representation 4711. We are looking for its representation in the twelve system.
To get this representation, divide the given representation step by step by the new base 12. The remaining remainders provide the representation for base 12. The first remainder corresponds to the lowest digit value of the new representation sought (in our case the position ), the the second remainder corresponds to the second lowest digit value (i.e. the position ) etc. The corresponding calculation is therefore:
- 4711 divided by 12 results in 392 remainder 7 (corresponds to the digit for the position in the result)
- 392 divided by 12 results in 32 remainder 8 (corresponds to the digit for the position in the result)
- 32 divided by 12 results in 2 remainder 8 (corresponds to the digit for the position in the result)
- 2 divided by 12 results in 0 remainder 2 (corresponds to the digit for the position in the result)
As a duodecimal representation of the given number, we get 2887. The conversion to other place value systems is done analogously.
Example 2: Conversion of a representation on base 16 into a representation on base 10
Regarding the hexadecimal system with the digits 0, 1,…, 9, A (value 10), B (value 11), C (value 12), D (value 13), E (value 14) and F (value 15) a number representing MONKEY. We are looking for the representation of this number in the decimal system.
In order to get this representation, one multiplies the numerical values of the given representation with the respective place values and adds up the results. The associated invoice is therefore:
- 10 (A) times results in 40960
- 15 (F) times is 3840
- 15 (F) times is 240
- 14 (E) times is 14
As a decimal representation of the given number we thus get . The conversion into other place value systems takes place analogously.
Example 3: decimal places
With regard to the tens system, a number is represented by 0.1. We are looking for the representation of this number in the dual system.
To do this, the fractional part is repeatedly multiplied by the base of the target system. If a value greater than 1 occurs, its whole number is added to the number of decimal places, otherwise a 0 is added to the decimal places. If an integer occurs as a multiplication result, the amount after the decimal point is fully determined, but a period will often also occur.
The associated invoice is therefore:
- 0.1 times 2 results in 0.2, so the first decimal place is 0
- 0.2 times 2 results in 0.4, so the second decimal place is 0
- 0.4 times 2 results in 0.8, so the third decimal place is 0
- 0.8 times 2 results in 1.6, so the fourth decimal place is the 1
- 0.6 times 2 results in 1.2, so the fifth decimal place is the 1
- 0.2 times 2 (does not have to be executed anymore because a period has occurred)
The result obtained is thus 0.0001100110011 ...
Balanced value systems
The balanced systems are special value systems. They always have an odd base and use both natural and negative digit values, namely those from the set . Often the negative digits are indicated by an underscore. So z. For example, in the balanced ternary system, a number is represented by the digits 1 , 0 , and 1 , to which the values −1, 0 and 1 are assigned.
A balanced ranking system has the following properties:
- The negative of a number is obtained by exchanging each digit with its inverse counterpart.
- The first digit different from 0 shows the sign . The system can do without a separate sign.
- Rounding to the next whole number is done by simply truncating the comma.
The representation of the whole numbers is clear.
But there are rational numbers that cannot be clearly represented. For this, be the largest digit and the smallest, then e.g.
Lexicographical order
With a positive base , the usual order relation of the real numbers is closely related to the lexicographical order of the -adic character strings representing these numbers . More accurate:
- There is an order homomorphism (an order-preserving mapping) , which maps the arbitrarily (also infinitely) long character strings in a -adic way into a real interval.
- For no -adic system, is injective .
- Which real numbers have multiple representations (multiple archetypes) depends on the digit values of the associated digit system . Their set is a subset of the rational numbers, so it has countable power. It lies close to the image interval.
| Derivation |
|
Be this and a strictly totally ordered alphabet with the order relation with was called. Furthermore, if two characters are with , then is lexicographical for all strings with as the set of arbitrarily (also infinitely) long strings above (including the Kleenian envelope of ). The character strings can also be understood as -adic representation, namely the values of the digits consecutively defined without gaps, so
so that a minimal set of digits for an -adic system and is. We limit ourselves to numerical values, the amount of which is not greater than the base, i.e. (which covers the most important cases that occur in practice). The digits can be chosen so that is. This is compatible with , and the above lexicographical inequality remains valid, even if the chains and have periods continued into infinity. A continuation is required to evaluate the character strings according to the -adic system the value function with for and with
With respect to the metric of the ordinary Archimedean absolute value, the series converge and
and it is
This applies lexicographically (and the strings are obviously different in ), but they are on the same real number pictured. Thus it is not injective. If one includes equality in the order relations, then applies and is a Ordnungshomomorphismus , but not the bijective and so no Trim iso is momorphismus. In the section Representation of Rational Numbers , the set of real numbers with finite representation was worked out. The set of real numbers with multiple representation is then
thus at the same as that of the finite representations; so with many common -adic systems. |
Generalizations
Number systems with mixed bases
An obvious generalization is to choose different bases for the different digit positions. One then speaks of number systems with mixed bases. A couple of interesting examples are:
- alternating a or b , where a and b are two different natural numbers> 1
- 2 or 3, however, in the order that “relatively closest” is approximated with the product of the first k bases
- the natural numbers> 1 are used in sequence as the basis ( "factorial basis" )
- the prime numbers in sequence or the (then repeating) prime numbers that occur with each next higher prime number power (see also representation of the per-finite numbers with several bases )
In the last two cases, one basically has to provide an infinite number of different digit symbols.
Date format as a number system with mixed bases
The representation of the date and time also traditionally has several bases and number systems. In the present context, the only example is the following representation, which is common in the Anglo-Saxon language area
- [1-12] [1-31] [0-9] [2,4, *] [1-12] [am, pm] [0-59] [0-59] [0-9] *
in which the order of year, month and day on the one hand and half-day and hour on the other hand are reversed contrary to the order of precedence. Bases 2, 10, 12, 28-31 and 60 are used here. It is particularly noteworthy that the basis of the day digit is based on the value of the month digit.
Non-natural numbers as a basis
The base does not necessarily have to be a natural number. All (even complex) numbers with an amount greater than 1 can be used as the basis of a place value system.
Negative bases
Positional notation with negative bases with cooperating with the same numerals inventories as their positive equivalents and is often called Radix referred. They are often identified with the prefix nega- , for example the negadecimal e, negabinary e, negaternary e, etc. place value system.
These value systems get by without an extra sign. On the other hand, the representations often require one digit more than in the corresponding system with a positive base. Furthermore, the arithmetic operations, in particular the arithmetic comparison and the formation of the absolute value, are somewhat more complex.
If the number of digits is minimal, for example , then all whole numbers can be clearly represented. As with the positive bases, there are rational numbers that cannot be clearly represented. Be to it
and the largest digit then is both
as well as
The English-language article provides some arithmetic operations .
Irrational bases
If one wants to represent all real numbers, then the minimum size of the number system (absolute bars and Gauss brackets ) must be with a non-integer or irrational basis . Some of the statements made here about the finite representability of rational numbers do not apply to such generalized place value systems.
If, for example, the golden ratio is used as the basis and as a set of digits, then a finite sequence of digits always represents an integer or an irrational number of the form with rational . Nevertheless, not every such number has a finite representation.
Another representation based on the golden ratio is the Zeckendorf representation , in which, however, not the powers of , but the Fibonacci numbers are used as place values.
Non-real bases
The first number system that does not represent a complex number as two separate digit sequences - one for the real part and one for the imaginary part - but rather a complex number as a single digit sequence was the "quater-imaginary" system proposed by D. Knuth in 1955. It has as base and 0 , 1 , 2 , 3 as digits. There is, for example, and . See also the English article en: Quater-imaginary base .
Another system was proposed by S. Khmelnik in 1964 and worked out for digital machinery. It has as base and 0 , 1 as digits. E.g. is and . See also the English article en: Complex base systems .
p -adic numbers
The place value systems presented here are based on the convergence in relation to the metric of the ordinary Archimedean absolute value. The infinite series - which here always converge "to the right" with the small powers of the base (exponents ) - are then real (or complex) numbers. But there are also metrics for the rational numbers that are based on non-Archimedean amount functions and allow a very similar notation with a base and a set of digits. The infinite series - which also always converge there, namely to the "left" by convention for the large powers (exponents ) - are p -adic numbers .
Although finite -adic expressions agree with the same sequence of digits in (then also finite) -adic representation, there are serious differences to the (Archimedean) systems presented here. The most important are:
- The -adic representations are always (reversible) unique.
- A sign is not required. The representation of as an infinite sum is .
- A -adic ring cannot be arranged .
- Is decomposable, i.e. not a prime number, then the -adic ring contains zero divisors (all of which have non- terminating representations). Details in Profinite # 10-adic Numbers .
- The non- terminating series in both systems represent number objects with completely different arithmetic properties. The periodic series among them represent rational numbers in both systems.
- All algorithms for the basic arithmetic operations start on the right with the small exponents (possibly negative, but ) and, like the powers and carries, run in the same direction to the left to the large exponents. If the invoice is canceled, the size of the error can be indicated immediately.
Further texts
The article Divisibility explains how in the representation of place value systems it can be recognized in certain cases whether one number is a divisor of another. The Cantor normal form generalizes the representation of numbers in place value system on ordinals .
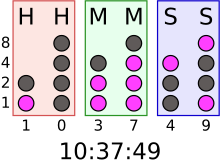
The Berlin clock shows an application example .
literature
- Donald Knuth : The Art of Computer Programming . 3. Edition. tape 2 . Addison-Wesley, Boston 1998, ISBN 0-201-89684-2 , Positional Number Systems, pp. 194-213 (English).
Web links
- Online converter for various number systems ( JavaScript )
- Converter for bases 2, 8, 10 and 16
- "Grandpa" system of the Tyrolean elementary school teacher Anton Haag
- Video: Place Value Systems (Part 1) . University of Education Heidelberg (PHHD) 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19902 .
- Video: Place Value Systems (Part 2) . Pedagogical University of Heidelberg (PHHD) 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19903 .
References and comments
- ↑ The case means a set of digits consisting of a single element, so that the only possible distinguishing feature between two representations is their length. In the best case, this leads to the unary system , a not so powerful representation system, which is not considered a place value system, since the value of a digit is always the same regardless of its position.
- ↑ DIN 1333, chap. 8th
- ↑ a b DIN 1333 , numbers , 1992, chap. 10.1
-
↑ Number systems with negative number values are also of interest, especially the balanced place value systems . The systems by David W. Matula (quoted from # Knuth1, p. 210f ) are rather exotic .
However, they all contain the zero, since otherwise the zero itself cannot be displayed and a broken display differs from the exact number by more than the smallest place value. - ↑ A notation of this kind, with the value descending from left to right , has been retained in data processing in the Big-Endian format .
- ↑ In the case of one is not the discrete valuation ring with confused about which also is dense in whose imprinted rating but for completely different completion , namely p -adischen numbers leads.
- ↑ This phenomenon occurs with every base and every "reasonable" number system. For see the section #Lexicographical order , for the section #Negative bases , each with examples for numbers with multiple representation.
- ↑ It is very similar with the Hilbert curve .
- ↑ Your measure is 0 and thus also the numbers with multiple representations.
- ^ A b c Levi Leonard Conant: The Number Concept . Etext, Project Gutenberg (English)
- ↑ Nonetheless injective, if restricted to the Kleenian envelope (character strings of finite length).
- ↑ Petkovšek p. 408
- ↑ As above with the powers of two, such a representation can be understood as a “special case” of an ab -adic.
- ↑ If each position is assigned its own number (or several), the result is an addition system .
- ↑ Based on cycles of the real world, only day, month and year are used (the incommensurability of which is compensated with considerable organizational effort (e.g. by introducing a leap year ). All other idiosyncratic representations are human artifacts with an extraordinary permanence.
- ^ Donald Knuth : An imaginary number system . In: Communications of the ACM . 3, No. 4, April 1960.
- ↑ SI Khmelnik: Specialized digital computer for operations with complex numbers . In: Questions of Radio Electronics (in Russian) . XII, No. 2, 1964.









































![{\ displaystyle [b] \ in \ mathbb {Z} _ {n} ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43b7cf4ebd4ef899254f291c0ea1d54b7347cd86)






























































![{\ displaystyle w \, \ colon \ Sigma \ to [-b, + b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e9dcd582ad4af8c501aa95c6e747fc3f2c2d96)



![{\ displaystyle \ omega \, \ colon \ Sigma ^ {\ infty} \ to [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e11e6620a75c5d08fa192137604a7b220a3afa0a)

![{\ displaystyle \ omega (z) = w (z) / b \; \ in [-1.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6493636c34ba2a162b05b36fe71a64451e808f37)





![{\ displaystyle \ omega (Ss) = (w (S) + \ omega (s)) / b = (w (T) -1+ \ omega (t) +1) / b = (w (T) + \ omega (t)) / b = \ omega (Tt) \; \ in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c160e5fc54291a768af4c6e18832a505c4e9ad34)










































