Mayan Calendar
As an astronomical calendar, the Maya calendar is the historical calendar system of the Maya . It is the most developed calendar of the Mesoamerican Native Americans .
.jpg)
overview
The Maya used for ritual and civil use different and complementary calendars that on a daily count in twenties system based: the ritual Tzolkin - Calendar, civil Haab - calendar and the Long Count , could be recorded with the extended periods required for celestial observations and historical records played a major role. The combinations of Tzolkin and Haab dates repeat after a calendar round of 52 years .
With its 365 days, the Haab resembles a solar calendar , but it cannot be described as such without a leap day rule . The 5 extra days of the 19th month are not leap days, but have the character of epagomens . Without being tied to the phases of the moon , the Haab is not a lunar calendar . In contrast to most other historical and modern calendar systems, the Tzolkin calendar is not tied to the rhythm of the sun or the moon. There have been numerous speculations as to which astronomical or other requirements this complex system follows. A conclusive answer is still pending and is currently not to be expected due to the poor source situation.
The three components of the Mayan calendar
Long count
The Maya used the long count of days for astronomical calculations and for recording history. The individual positions (like 9.12.11.5.18 ) each run from [0..19], [0..19], [0..19], [0..17], [0..19], wherein the first Baktun the calendar instead of 0 Baktun once deviating 13 Baktun was called. The long count therefore represents a date with which each day since the beginning of the calendar on August 11, 3114 BC. BC (13.0.0.0.0 4 Ahau 8 Cumku) can be clearly stated. The oldest Maya monument found so far with the date 7 Baktun 16 Katun 3 Tun 2 Uinal 13 Kin can therefore be dated December 5, 36 BC. To date.
It is noticeable that the beginning of the calendar (13.0.0.0.0 4 Ahau 8 Cumku) and the beginning of the next baktun (13.0.0.0.0 4 Ahau 3 K'ank'in = December 21 or 23, 2012) Date component 4 Ahau of the Tzolkin calendar included. According to Mayan mythology, the Tzolkin date 4 Ahau refers to the first four people or masters (Ahau) of the present creation, the man from corn. The repetition of this date component after 13 Baktun is no accident. Because the smallest common multiple of the 260-day Tzolkin calendar and a 144,000-day baktun is reached after 1,872,000 days (= 13 baktun). It can be shown mathematically that this property also applies to all other time units of the long count from the uinal. The significant Tzolkin date 4 Ahau also occurs after 13 Uinal, 13 Tun, 13 Katun, 13 Pictun, 13 Calabtun etc., as can easily be checked. According to the author Marcel Polte, this is also the answer to the hitherto unanswered question why the Maya used a period of 360 days as a basis for the Long Count as a "year" or do, although they have very precise knowledge of the actual duration of the Solar year and the Haab calendar also included 365 days. By shortening the “year” to a do with 360 days, the 4 Ahau date could be set again after 13 do cycles; this would not have worked for doing 365 days.
Periods
Kin, Uinal, Tun, Katun, Baktun , Pictun, Calabtun, Kinchiltun and Alautun are names for periods in the long count of the Maya calendar. The names higher than Baktun are modern inventions by researchers, the original names are not known. These high numerical values only appear in a small number of inscriptions and in the Dresden Mayan Code .
| Importance position | calculation | Numerical value | Surname | Logogram (s) |
|---|---|---|---|---|
| 1 | 1 | 1 | k'in |
|
| 2 | 20 k'in | 20th | uinal |
 
|
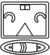
| 3 | 18 uinal | 360 | to do |
  
|
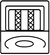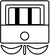
| 4th | 20 do | 7,200 | k'atun |
|
| 5 | 20 k'atun | 144,000 | baktun |
 
|
| 6th | 20 baktun | 2,880,000 | pictun | |
| 7th | 20 pictun | 57,600,000 | calabtun | |
| 8th | 20 calabtun | 1,152,000,000 | kinchiltun | |
| 9 | 20 kinchiltun | 23,040,000,000 | alautun |
Haab
The Haab was used by the Maya for civil purposes, such as calculating the sowing and harvesting times, and is similar to our calendar, since with 365 days it covers around one solar year. In the Haab calendar, the year is divided into 18 “months” with 20 days each and the 19th “month” with 5 “unlucky days”. According to Diego de Landa , the Maya also inserted a leap day every fourth year. However, de Landa does not provide any information about how the parallel run of Haab and Tzolkin was preserved. In the absence of other sources, it is therefore not known whether leap days were actually used. For this reason, no statement can be made about the beginning of the year of the Haab in pre-Hispanic times.
- Standard forms of enrollment (?) Up to month 4 and 15th
Month 01:
Pop
Month 02:
Uo
Month 03:
Zip
Month 04:
Zotz (Sotz ')
Month 05:
Zec (sec)
Month 06:
Xul
Month 07:
Yaxkin (yaxk'in)
Month 08:
Mol
Month 09:
Chen (Ch'en)
Month 10:
Yax
Month 11:
Zac (Sak)
Month 12:
Ceh
Month 13:
Mac (Mak)
Month 14:
Kankin
Month 15:
Muan
Month 16:
Pax
Month 17:
Kayab
Month 18:
Cumku
Month 19:
Uayeb / Wayeb ("unlucky days "; additional month with only 5 epagomens )
Tzolkin
For ritual purposes the Maya used the Tzolkin ("counting the days"), in which each day ( Kin ) is designated by a combination of a number (tone) from 1 to 13 with the name of one of 20 protective deities (or day names). A Tzolkin date therefore designates a specific day in a period of 260 days and is given as 6 Edznab , for example .
Calendar round
Since the Haab calendar has 365 days and the Tzolkin calendar has 260 days, the combinations of Haab and Tzolkin dates repeat every 18,980 days or 52 Haab years or 73 Tzolkin years. This period is called the calendar round, within which a combination of Haab and Tzolkin dates is clear.
Complete date and conversion
| Date part | Calculation with importance | Subtotal [days] |
|
|---|---|---|---|
| 9 | Baktun periods | 9 × 144,000 | 1,296,000 |
| +12 | Katun periods | 12 × 7,200 | 86,400 |
| +11 | Do-periods | 11 × 360 | 3,960 |
| + 5 | Uinal periods | 5 × 20 | 100 |
| +18 | Kin (days) | 18 × 1 | 18th |
| Sum of the date parts | 1,386,478 | ||
The day of death (August 31, 683) of the ruler Pakal I of Palenque is in the Mayan calendar 9.12.11.5.18 6 Edznab 11 Yax:
- 9.12.11.5.18 indicates the day as a long count
- 6 Edznab the day in the Tzolkin calendar and
- 11 Yax is the day in the Haab calendar.
This means: Pakal I of Palenque died 1,386,478 days after the creation of the world (August 13, 3114 BC).
For the conversion of a date of the Maya calendar into other calendar systems, in particular the European Julian or Gregorian calendar , a correlation number is used, which indicates the difference between the numerical value of the long count of the Maya and the Julian day . Despite numerous different approaches, the so-called Thompson equation of 584.284 ± 1 day is accepted and applied by the majority of experts.
"Doomsday Day"
Particular attention was paid to December 21st and 23rd, 2012 in esoteric circles. One wanted to recognize an alleged " Doomsday " of the Maya creation here. According to Mayan researchers, this was completely inaccurate in terms of content. It is correct that on this day in the Long Count for the first time since the year 3114 BC. The numerical value of the starting day of the current thirteenth Baktun cycle of the Long Count (13.0.0.0.0) returned. According to the scheme of the Maya calendar, this numerical value occurs regularly after 1,872,000 days (approx. 5128 years). However, the dates of the Long Count differ when they return due to a different position in the Haab year. The date 13.0.0.0.0 falls in the year 3114 BC. BC on day 8 Cumku, in 2012 on day 3 Kankin, then on 18 Ch'en etc. The Maya have demonstrably calculated far into the past as well as into the future over the end day of the Baktun cycle and with these dates mythical-dynastic events connected. This is what a throne jubilee of the ruler Pakal in 4772 is called.
The date 13.0.0.0.0 4 Ahau 8 Cumku was regarded by the Maya as the day of the creation of the world in its present form. However, so far no inscriptions have been discovered that would indicate the beginning of a new creation on the day 13.0.0.0.0 4 Ahau 3 Kankin in 2012. Only the inscription monument 6 from the (no longer existing) site El Tortuguero west of Palenque refers to this date and speaks somewhat cryptically of the fact that on this day the deity Bolon Yokte 'K'uh in a great act of clothing and presentation (one Official) will occur.
A publication by Science reports on the discovery of a calendar from the 9th century in the ruins of the Mayan stronghold of Xultun in what is now Guatemala . US researchers have discovered wall paintings from the 9th century there that show not only human figures but also the oldest Mayan astronomical calendars to date. Study director William A. Saturno says: "The ancient Maya predicted that the world would go on and that in 7000 years things would be exactly as they are today".
See also
- List of calendar systems
- Maya Codices , more precisely Codex Dresdensis - source for the discovery of the Maya calendar system
literature
- Linda Schele , David Freidel: The unknown world of the Maya. Albrecht Knaus, Munich 1991, ISBN 3-8135-6342-1 .
- Hugo Stamm : Under the spell of the Maya calendar - end time hysteria in sects and esotericism. Gütersloher Verlagshaus, 2012, ISBN 978-3-579-06674-5
Web links
- Codex Dresdensis - Mscr.Dresd.R.310 Dresden Mayan manuscript of the Saxon State Library - State and University Library Dresden online
- The Mayan Calendar
Individual evidence
- ↑ Herbert Metz: The basics of the Julian and Gregorian calendar. In: computus.de. 2002, accessed February 24, 2010 .
- ↑ Jens Rohark, Mario Krygier: Don Eric and the Maya. December 23, 2012. Will the gods come back? docupoint, Magdeburg 2006, p. 145
- ↑ Marcel Polte: 2012. Countdown of the Apocalypse? - A search for clues. Books on Demand, Norderstedt 2010, p. 58 f.
- ↑ Marcel Polte: 2012. Countdown of the Apocalypse? - A search for clues. Books on Demand, Norderstedt 2010, p. 59 f.
- ↑ Diego de Landa : Report from Yucatán, Reclam, Stuttgart p. 100.
- ↑ Nikolai Grube (ed.): Maya. Tandem Verlag, China 2007/2007, p. 135
- ^ Hanns J. Prem : Manual de la antigua chronología mexicana. CIESAS, México 2008, ISBN 978-968-496-694-9 .
- ↑ Linda Schele , David Freidel: The unknown world of the Maya. Albrecht Knaus, Munich 1991, p. 74.
- ↑ Linda Schele, David Freidel: The unknown world of the Maya. Albrecht Knaus, Munich 1991, p. 511 f.
- ^ Elisabeth Wagner, in Nicolai Grube (ed.): Maya. God kings in the rainforest. hfullmann, 2007, p. 283.
- ↑ Bernd Ingmar Gutberlet: The Maya calendar. Ehrenwirth, Bergisch Gladbach 2009, p. 240.
- ^ Elisabeth Wagner, in Nicolai Grube (ed.): Maya. God kings in the rainforest. hfullmann, 2007, p. 281.
- ↑ Sven Gronemeyer, Barbara MacLeod: What Could Happen in 2012: A Re-Analysis of the 13-Bak'tun Prophecy on Tortuguero Monument 6 (PDF; 9.9 MB) . In: Wayeb Notes. No. 34, 2010, p. 4 ff.
- ^ William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi: Ancient Maya Astronomical Tables from Xultun, Guatemala . In: Science. Vol. 336, May 11, 2012, pp. 714-717.
- ↑ No end of the world for the Maya. On: Wissenschaft.de on May 10, 2012. Retrieved on September 10, 2019.
- ↑ Dagmar Röhrlich: Old calendar: So far, the oldest astronomical calendar of the Maya discovered . In: Deutschlandfunk , May 11, 2012. Accessed July 30, 2012.