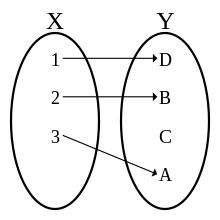
Injective function
Injectivity or uniqueness to the left is a property of a mathematical relation , in particular of a function (for which one usually says "mapping"): An injective function, also known as an injection , is a special case of a unambiguous left-hand relation , namely the one in which the relation is also right-clear and left-total .
A function is injective if for each element of the target set there is at most one (i.e. possibly none) element of the initial or definition set that aims at this, i.e. if two different elements of the definition set are never mapped to the same element of the target set:
The target set cannot therefore be less powerful than the definition set, i.e. that is, it cannot contain fewer elements.
The image set may be a true subset of the target set , i.e. In other words , there may be elements that are not picture elements , as is the case in the graphic shown on the right. This makes the difference to a bijective mapping, of which, besides injectivity, it is also required that each element of the target set appear as a picture element , that is, that it is surjective .
That a figure is injective is sometimes expressed by, with a symbol composed of and . It is reminiscent of the embedding of a set in a superset through a function that maps each element to itself.
Examples and counterexamples
- Extra-mathematical example: The function that assigns the number of their current identity card to every citizen of the Federal Republic of Germany with an identity card is injective, whereby the set of all possible identity card numbers is assumed as the target quantity (because identity card numbers are only issued once).
- denote the set of natural and the set of integers .
- is injective.
- is injective.
- is injective.
- is not injective, as e.g. B. applies.
- Any function from a two- element set to a one- element set is not injective, because both elements are necessarily mapped to the single element :
- in spite of
properties
- Note that the injectivity of a function only depends on the function graph (in contrast to surjectivity , which also depends on the target set , which cannot be read from the function graph).
- A function is injective if and only if the following applies to all subsets :
- A function is injective if and only if it holds for all (where the archetype function denotes).
- If the functions and are injective, then the composition (concatenation) is also injective.
- From the injectivity of it follows that is injective.
- A function with a non-empty set of definitions is injective, when a left inverse has, which is a function with (where the identity mapping to hereinafter).
- A function is injective if they linkskürzbar is, so if for any function of the equality follows. (This property motivates the term monomorphism used in category theory , however, for general morphisms, injective and left- shortable are no longer equivalent.)
- Any function can be represented as a chaining , where is surjective and injective (namely an inclusion mapping ).
- A continuous real-valued function on a real interval is injective if and only if it is strictly monotonically increasing or strictly monotonically decreasing in its entire domain , i.e. That is, if the following applies to any two numbers and from the domain of definition: From follows (rising), or from follows (falling).
- A group or vector space homomorphism is injective if and only if its kernel is trivial, i.e. H. consists only of the neutral element or the zero vector .
Cardinalities of sets
The concept of injection plays an important role in set theory in the definition and comparison of cardinalities , a concept that generalizes the number of elements of finite sets to arbitrary sets. Two sets are said to be “of equal power” if there is both an injection from to and one from to . (In this case there are also bijections from one set to the other.) On the other hand, it is said to be less powerful than if there is an injection from to but not from to .
Drawer closure
An inference scheme that is frequent in proofs, especially of number theory, uses the statement that a mapping of a finite set into a set with fewer elements cannot be injective, i.e. that there are elements with and the same image . Because of the idea of many objects in fewer drawers, this is called “ drawer closure ”.
Number of injective images
The number of injective mappings from a definition set into a given finite target set with the property is given by:
In combinatorics, this corresponds to a variation without repetition.
history
After having managed for generations with formulations like “one-to-one”, the need for a more concise designation arose only in the middle of the 20th century with the consistent set-theoretical representation of all mathematical sub-areas.
In English, the noun injection 1945 can be used. The English adjective injective was used in the Foundations of algebraic topology by S. Eilenberg and N. Steenrod in 1952 , but more in the sense of injective objects . Injective in context with the technical terms surjective and bijective was introduced in 1954 by the group of authors Nicolas Bourbaki in the book Théorie des ensembles, Éléments de mathématique Première Partie .
In places there is great confusion regarding the assignment between the terms “one-to-one” on the one hand and “injective” or “bijective” on the other. Sources (textbooks) from pure mathematics favor “injective”, non-subject sources tend to favor “bijective”.
Individual evidence
- ^ Ralph H. Fox : Torus homotopy groups . In: Proceedings of the National Academy of Sciences . tape 31 , no. 2 , February 1, 1945, p. 71–74 , see p. 73 ( online [PDF; accessed on January 13, 2017]): "The nucleus of the injection homomorphism ..."
- ^ A b Earliest Known Uses of Some of the Words of Mathematics.