Injective object
Injective object is a term from the mathematical branch of category theory .
definition
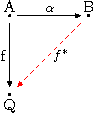
In a category an object is injective if for any monomorphism and every one is, so is.
Accordingly, it is injective if and only if the induced mapping is surjective for all monomorphisms .
Examples
- In the category of sets Me , every set is injective.
- Injective objects in the category of Abelian groups are the divisible groups ; H. those groups for which multiplication by a non-zero integer is surjective; Examples are and .
- In the category of vector spaces over a body, every object is injective.
- Every terminal object in a category is injective.
- If there is a family of injective objects, the product of that family is injective if it exists.
- If the category has a null object, then a product of injective objects is injective if and only if each is injective.
- If injective, then every monomorphism is a cut (that is, there is a with ).
- In the category of topological spaces, the set is not injective because the inclusion map is not a section. There is no such thing as a continuous surjective function . This is a consequence of the intermediate value theorem .
Injective modules
For a right module over a ring , the following statements are equivalent.
- is injective in the category of legal modules.
- For every monomorphism there is one with . It is the identity .
- Baer's criterion : For every legal ideal and every homomorphism there is one such that is.
Injective modules were introduced in 1940 by Reinhold Baer who, however, used the adjective complete instead of injective . The German designation injective module can be proven in 1953.
Examples
- A ring is semi-simple if and only if every module above the ring is injective. Hence every vector space over a sloping body is injective. From Baer's criterion it follows that precisely the divisible modules are injective via main ideal rings. A module is divisible if and only if is for all ring elements .
- If there is a family of modules, then the direct product of the family is injective if and only if each is injective.
- A ring is Noetherian if and only if the direct sum of injective modules is injective. This is a generalization of the corresponding statement about divisible Abelian groups.
- Above a hereditary (hereditary) ring, each epimorphic image of an injective module is injective. This is a generalization of the corresponding theorem about divisible groups.
- A torsion-free module is injective via an integrity ring exactly when it can be divided.
- If there is a unitary ring homomorphism, there is an S-module on both sides. If there is another S-module, then the set of S-homomorphisms on the right-hand side carries through an R-module structure . The following applies: If an S module is injective, then an injective R module is. This is especially important in the case . If a divisible group is injective as a module, it is an injective R module.
There are enough injective modules
Each module can be mapped monomorphically into an injective module.
Injective sheath
A sub-module is called large if it is the only sub-module of that has an average . A monomorphism is called essential if large is in. The following applies:
Each module can essentially be mapped into an injective module . The module is uniquely determined by this property except for isomorphism. It is called the injective hull of M and is often referred to as.
Indecomposable injective modules
A module is called directly indivisible if it is not the direct sum of two sub- modules not equal to zero. The following statements are equivalent for a module .
- Any sub-module other than the null module is large in .
- The injective shell cannot be dismantled directly.
- is the injective envelope of each sub-module not equal to zero.
- The ring of endomorphisms of is local .
A module that satisfies the equivalent properties of the set is called uniform . is then often called irreducible (average irreducible ).
Examples
- Every simple module is uniform, so it has an injective shell that cannot be dismantled.
- If there is a prime ideal in the commutative ring , then is uniform. In particular, every integrity ring is uniform as a module.
Individual evidence
- ^ Friedrich Kasch, "Modules and Rings", Teubner, Stuttgart 1977, page 113, ISBN 3-519-02211-7
- ↑ Reinhold Baer : Abelian groups that are direct summands of every containing abelian group . In: Bulletin of the American Mathematical Society . tape 46 , no. October 10 , 1940, p. 800-806 , doi : 10.1090 / S0002-9904-1940-07306-9 .
- ↑ B. Eckmann , A. Schopf: About injective modules . In: Archives of Mathematics . tape 4 , no. 2 , April 1953, p. 75-78 , doi : 10.1007 / BF01899665 .
- ^ Friedrich Kasch, "Modules and Rings", Teubner, Stuttgart 1977, page 114, ISBN 3-519-02211-7
- ^ Friedrich Kasch, "Modules and Rings", Teubner, Stuttgart 1977, page 118, ISBN 3-519-02211-7