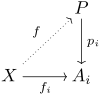Product of modules

In many areas of mathematics, direct products and coproducts of the objects under consideration play a special role. The construction of such products of object families is often based on the Cartesian product of sets.

In set theory , the Cartesian product of a family of sets is defined as follows: ${\displaystyle (A_{i}|i\in I)}$

${\displaystyle {\begin{aligned}\prod _{i\in I}A_{i}:&=\{a:I\rightarrow \bigcup _{i\in I}A_{i}|a(i)\in A_{i}\quad \forall i\in I\}\end{aligned}}}$

If they are all right modules above the unitary ring , it has a module structure. This is a product of modules , the product of the module family . ${\displaystyle A_{i}}$ ${\displaystyle R}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle (A_{i}|i\in I)}$

Definition of the product

Product of modules

If there is a family of right modules above the ring , the product of the modules is called. Is is the name of the -th component of . The product is given a module structure through the following two links. ${\displaystyle (A_{i}|i\in I)}$ ${\displaystyle R}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle \textstyle a\in \prod _{i\in I}A_{i}}$ ${\displaystyle a(i)}$ ${\displaystyle i}$ ${\displaystyle a}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$

${\displaystyle {\begin{aligned}+&:\prod \limits _{i\in I}A_{i}\times \prod \limits _{i\in I}A_{i}\ni (a,b)\mapsto a+b\in \prod \limits _{i\in I}A_{i},\quad {\mbox{ wobei }}(a+b)(i):=a(i)+b(i),\,i\in I\\\cdot &:\prod \limits _{i\in I}A_{i}\times R\ni (a,r)\mapsto a\cdot r\in \prod \limits _{i\in I}A_{i},\quad {\mbox{ wobei }}(a\cdot r)(i):=a(i)\cdot r,\,i\in I\end{aligned}}}$

If the function is , it is often written for it in the same way as is usual for real number sequences. Where is the -th component. So you add component by component and multiply with the scalars component by component. ${\displaystyle \textstyle a\in \prod _{i\in I}A_{i}}$ ${\displaystyle (a_{i})}$ ${\displaystyle a_{i}=a(i)}$ ${\displaystyle i}$

Universal property of the product

If the product of the modules is then the functions map the product epimorphically to . They are called projections . The couple has the following characteristic: ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle \pi _{i}\colon \prod \limits _{i\in I}A_{i}\ni (a_{i})\mapsto a_{i}\in A_{i}}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle \textstyle (\prod _{i\in I}A_{i},(\pi _{i},i\in I))}$

For every right module over and each family of homomorphisms there is a homomorphism precisely so that all true. ${\displaystyle X}$ ${\displaystyle R}$ ${\displaystyle f_{i}:X\rightarrow A_{i}}$ ${\displaystyle \textstyle f\colon X\to \prod _{i\in I}A_{i}}$ ${\displaystyle \pi _{i}\circ f=f_{i}}$ ${\displaystyle i\in I}$

In category theory , such a property is called universal ; it characterizes the product of objects down to isomorphism, that is:

If there is a module and a family of homomorphisms and there is exactly one with for every module and every family of homomorphisms , then is . A diagram for this situation looks like this: ${\displaystyle P}$ ${\displaystyle p_{i}\colon P\rightarrow A_{i}}$ ${\displaystyle X}$ ${\displaystyle f_{i}\colon X\to A_{i}}$ ${\displaystyle f\colon X\to P}$ ${\displaystyle p_{i}\circ f=f_{i}}$ ${\displaystyle \textstyle P\cong \prod _{i\in I}A_{i}}$

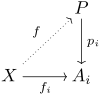
The above construction together with the verification of the universal property can also be briefly summarized as follows: There are products in the module category.

Product and hom functor

If there is a family of homomorphisms, then is a product of the family if and only if the homomorphism ${\displaystyle p_{i}\colon P\rightarrow A_{i}}$ ${\displaystyle P}$ ${\displaystyle (A_{i}|i\in I)}$

${\displaystyle {\begin{aligned}Hom(M,P)\ni f&\mapsto (p_{i}\circ f)\in \prod _{i\in I}Hom(M,A_{i})\end{aligned}}}$

is an isomorphism for all right modules . In particular: ${\displaystyle M}$

${\displaystyle {\begin{aligned}\Phi (M)\colon Hom(M,\prod _{i\in I}A_{i})\ni f&\mapsto (\pi _{i}\circ f)\in \prod _{i\in I}Hom(M,A_{i})\end{aligned}}}$

a natural transformation that is an isomorphism for each module . is a functional isomorphism. ${\displaystyle M}$ ${\displaystyle \Phi (M)}$

Examples, remarks, designations

1. Is for everyone , one writes and calls this a power of . ${\displaystyle i\in I:A_{i}=A}$ ${\displaystyle \textstyle A^{I}:=\prod _{i\in I}A_{i}}$ ${\displaystyle A}$
2. For each index set there is even a ring if one multiplies component by component. is a module on the left and right side above the ring . The diagonal mapping is a homomorphism of the rings and the modules. All components are equal to r. ${\displaystyle I}$ ${\displaystyle R^{I}}$ ${\displaystyle R^{I}}$ ${\displaystyle R}$ ${\displaystyle R\ni r\mapsto (r)\in R^{I}}$ ${\displaystyle (r)}$
3. If there is a family of sub-modules, there is a clearly determined homomorphism with . Here is the family of canonical homomorphisms from to the factor modules . The core of this homomorphism is . ${\displaystyle U_{i}\hookrightarrow A_{R}}$ ${\displaystyle \textstyle f:A\rightarrow \prod _{i\in I}A/U_{i}}$ ${\displaystyle \pi _{i}\circ f=p_{i}}$ ${\displaystyle (p_{i}|i\in I)}$ ${\displaystyle A_{R}}$ ${\displaystyle A/U_{i}}$ ${\displaystyle \textstyle \bigcap \limits _{i\in I}U_{i}}$
4. If and are two families of modules and if is a family of homomorphisms, then the mapping is a homomorphism. It is . Next is . ${\displaystyle (A_{i}|i\in I)}$ ${\displaystyle (B_{i}|i\in I)}$ ${\displaystyle f_{i}\colon A_{i}\rightarrow B_{i}}$ ${\displaystyle \textstyle \prod f_{i}\colon \prod _{i\in I}A_{i}\ni (a_{i})\mapsto (f_{i}(a_{i}))\in \prod _{i\in I}B_{i}}$ ${\displaystyle \textstyle \operatorname {Kern} (\prod f_{i})=\prod _{i\in I}\operatorname {Kern} (f_{i})}$ ${\displaystyle \textstyle \operatorname {Bild} (\prod _{i\in I}f_{i})=\prod _{i\in I}\operatorname {Bild} (f_{i})}$
5. If it is also a family of modules and if the sequence is exact for all of them , then is exact. ${\displaystyle \textstyle (C_{i}|i\in I)}$ ${\displaystyle i\in I}$ ${\displaystyle \textstyle A_{i}{\stackrel {f_{i}}{\rightarrow }}B_{i}{\stackrel {g_{i}}{\rightarrow }}C_{i}}$ ${\displaystyle \prod _{i\in I}A_{i}{\stackrel {\prod f_{i}}{\rightarrow }}\prod _{i\in I}B_{i}{\stackrel {\prod g_{i}}{\rightarrow }}\prod _{i\in I}C_{i}}$
6. Are right modules, so there is a uniquely determined homomorphism with for all . It is . If the endomorphism ring is of , there is an S sub-module of on the left side . If so, the module creates the module . A module of all legal modules cogenerated's cogenerator . The module is therefore a co-generator if there is a monomorphism for each right module for a certain index set . ${\displaystyle A,Q}$ ${\displaystyle g:A\rightarrow Q^{Hom(A,Q)}}$ ${\displaystyle \pi _{f}\circ g=f}$ ${\displaystyle f\in Hom_{R}(A,Q)}$ ${\displaystyle \textstyle \operatorname {Kern} (g)=\bigcap _{f\in Hom(A,Q)}Kern(f)}$ ${\displaystyle S=Hom_{R}(A,A)}$ ${\displaystyle A}$ ${\displaystyle \operatorname {Kern} (g)}$ ${\displaystyle _{S}A}$ ${\displaystyle \operatorname {Kern} (g)=\{0\}}$ ${\displaystyle Q_{R}}$ ${\displaystyle A_{R}}$ ${\displaystyle Q_{R}}$ ${\displaystyle A_{R}}$ ${\displaystyle A\rightarrow Q^{I}}$ ${\displaystyle I}$
7. Is an Abelian group, then torsion if and only if from is cogenerated. ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \mathbb {Q} }$
8. ${\displaystyle \mathbb {Q} /\mathbb {Z} }$is a cogenerator in the Abelian group category. This is no longer easy. It assumes the theory of injective modules. See for example

Coproduct of modules

A function is called finite-valued if only holds for finitely many . You mean the same thing when you say for almost everyone . The set of finite-valued mappings from is called the coproduct (or outer direct sum) of the family and denoted by. is a sub-module of the product. ${\displaystyle \textstyle f\colon I\rightarrow \bigcup _{i\in I}A_{i}\,,f(i)\in A_{i}}$ ${\displaystyle \textstyle f(i)\neq 0}$ ${\displaystyle \textstyle i\in I}$ ${\displaystyle \textstyle f(i)=0}$ ${\displaystyle \textstyle i\in I}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle \textstyle (A_{i}|i\in I)}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$

If , let the following figure look like : ${\displaystyle a\in A_{j}}$ ${\displaystyle \eta _{j}(a)}$ ${\displaystyle \coprod _{i\in I}A_{i}}$

${\displaystyle {\begin{aligned}\eta _{j}(a)(i)&={\begin{cases}0&\mathrm {falls} \,i\neq j\\a&{\text{falls}}\,i=j\end{cases}}\end{aligned}}}$

If the mapping is written as a tuple, then is . In all places of the tuple there is 0, only in the jth place there is a. ${\displaystyle \eta _{j}(a)}$ ${\displaystyle \eta _{j}(a)=(\dots 0,a,0,\dots )}$

${\displaystyle \eta _{j}\colon A_{j}\ni a\mapsto \eta _{j}(a)\in \coprod _{i\in I}A_{i}\hookrightarrow \prod _{i\in I}A_{i}}$is the only homomorphism that fulfills the following condition: ${\displaystyle f\colon A_{j}\rightarrow \prod _{i\in I}A_{i}}$

${\displaystyle {\begin{aligned}\pi _{i}\circ f&={\begin{cases}0&{\text{falls}}\,i\neq j\\\mathbf {1} _{A_{j}}&{\text{falls }}\,i=j\end{cases}}\end{aligned}}}$

This results from the universal property of the product. They are all monomorphisms and it is the direct sum of the in the product of . ${\displaystyle (\eta _{i}|i\in I)}$ ${\displaystyle \coprod _{i\in I}A_{i}=\bigoplus _{i\in I}\eta _{i}(A_{i})}$ ${\displaystyle \eta _{i}(A_{i})}$ ${\displaystyle A_{i}}$

Universal property of the co-product

If the co-product of the modules is so form the functions ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$ ${\displaystyle A_{i}}$

${\displaystyle \eta _{i}\colon A_{i}\ni a\mapsto \eta _{i}(a)\in \coprod _{i\in I}A_{i}}$

the monomorphic after ab. They're called injections . The couple has the following characteristic: ${\displaystyle \textstyle A_{i}}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$ ${\displaystyle \textstyle (\coprod _{i\in I}A_{i},(\eta _{i},i\in I))}$

For every module and every family of homomorphisms there is exactly one homomorphism , so that applies to all . ${\displaystyle D_{R}}$ ${\displaystyle g_{i}:A_{i}\rightarrow D}$ ${\displaystyle \textstyle g\colon \coprod _{i\in I}A_{i}\rightarrow D}$ ${\displaystyle g\circ \eta _{i}=g_{i}}$ ${\displaystyle i\in I}$

In category theory , this universal property characterizes the co-product of objects down to isomorphism, that is:

If there is a module and a family of homomorphisms and there is exactly one with for every module and every family of homomorphisms , then is . ${\displaystyle S}$ ${\displaystyle q_{i}:A_{i}\rightarrow S}$ ${\displaystyle D}$ ${\displaystyle g_{i}\colon S\rightarrow D}$ ${\displaystyle g\colon S\rightarrow D}$ ${\displaystyle g_{i}=g\circ q_{i}}$ ${\displaystyle \textstyle S\cong \coprod _{i\in I}A_{i}}$

The above construction together with the verification of the universal property can also be briefly summarized as follows: There are co-products in the module category.

Coproduct and Hom functor

If there is a family of homomorphisms, then is a co-product of the family if and only if the homomorphism ${\displaystyle q_{i}\colon A_{i}\rightarrow Q}$ ${\displaystyle Q}$ ${\displaystyle (A_{i}|i\in I)}$

${\displaystyle {\begin{aligned}Hom(Q,M)\ni f&\mapsto (f\circ q_{i})\in \prod _{i\in I}Hom(A_{i},M)\end{aligned}}}$

is an isomorphism for all right modules . In particular: ${\displaystyle M}$

${\displaystyle {\begin{aligned}\Phi (M)\colon Hom(\bigoplus _{i\in I}A_{i},M)\ni f&\mapsto (f\circ \eta _{i})\in \prod _{i\in I}Hom(A_{i},M)\end{aligned}}}$

a functional isomorphism. ${\displaystyle \Phi (M)}$

Names and examples

1. Most of the time you identify with the in . Then you write instead of . Usually there is no confusion to worry about. ${\displaystyle \textstyle A_{i}}$ ${\displaystyle \textstyle \eta _{i}(A_{i})}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$ ${\displaystyle \textstyle \bigoplus _{i\in I}A_{i}}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$
2. Is that for everyone so you write instead of . ${\displaystyle \textstyle A_{i}=A}$ ${\displaystyle \textstyle i\in I}$ ${\displaystyle \textstyle A^{(I)}}$ ${\displaystyle \textstyle \coprod _{i\in I}A_{i}}$
3. Is for everyone , so is a free module . One basis is the family with . ${\displaystyle \textstyle A_{i}=R}$ ${\displaystyle \textstyle i\in I}$ ${\displaystyle \textstyle R^{(I)}}$ ${\displaystyle \textstyle (e_{i}|i\in I)}$ ${\displaystyle \textstyle e_{i}:=\eta _{i}(1)}$
4. If the index set is finite, the direct sum and direct product are identical. ${\displaystyle \textstyle I}$
5. Is a finite subset of and , then is a direct summand in . The homomorphism satisfies the conditions and . For infinite sets, the direct sum is usually by no means a direct summand in the direct product. So there is no direct summand in . A difficult question is: For which modules is the direct summand in the product ? If, for example, semi-simple and finitely generated, this is the case. ${\displaystyle E}$ ${\displaystyle \textstyle I}$ ${\displaystyle \textstyle A=\oplus _{i\in E}A_{i}}$ ${\displaystyle \textstyle A}$ ${\displaystyle \textstyle \prod _{i\in I}A_{i}}$ ${\displaystyle \textstyle p=\sum _{i\in E}\eta _{i}\circ \pi _{i}\colon \prod _{i\in I}A_{i}\rightarrow \prod _{i\in I}A_{i}}$ ${\displaystyle \textstyle p\circ p=p}$ ${\displaystyle \operatorname {Bi} (p)=A}$ ${\displaystyle \textstyle \mathbb {Z} ^{(\mathbb {N} )}}$ ${\displaystyle \textstyle \mathbb {Z} ^{\mathbb {N} }}$ ${\displaystyle \textstyle M}$ ${\displaystyle \textstyle M^{(\mathbb {N} )}}$ ${\displaystyle \textstyle M^{\mathbb {N} }}$ ${\displaystyle \textstyle M}$
6. Are right modules, so there is a uniquely determined homomorphism with for all . It is . If the endomorphism ring is of , there is an S sub-module of on the left side . Is , the module creates the module . A module that creates all right modules is called a generator . The module is therefore a generator if there is an epimorphism for every right module for a certain index set . Since each module is the epimorphic image of a free module, is a generator. ${\displaystyle G,A}$ ${\displaystyle \textstyle g:G^{(Hom(G,A))}\rightarrow A}$ ${\displaystyle g\circ \eta _{f}=f}$ ${\displaystyle f\in Hom_{R}(G,A)}$ ${\displaystyle \textstyle \operatorname {Bild} (g)=\sum _{f\in Hom(G,A)}\operatorname {Bild} (f)}$ ${\displaystyle \textstyle S=Hom_{R}(A,A)}$ ${\displaystyle \textstyle A}$ ${\displaystyle \operatorname {Bild} (g)}$ ${\displaystyle _{S}A}$ ${\displaystyle \textstyle \operatorname {Bild} (g)=A}$ ${\displaystyle G}$ ${\displaystyle A}$ ${\displaystyle \textstyle G}$ ${\displaystyle A}$ ${\displaystyle \textstyle G^{(I)}\rightarrow A}$ ${\displaystyle \textstyle I}$ ${\displaystyle \textstyle R_{R}}$

Two important sentences

A decomposition theorem by Kaplansky

Let be an infinite cardinal number. If the module is a direct sum of sub- modules that can be generated, then each direct summand of the direct sum of sub- modules that can be generated is. ${\displaystyle c}$ ${\displaystyle M}$ ${\displaystyle c}$ ${\displaystyle M}$ ${\displaystyle c}$

The most important case is: If the direct sum of countably generated sub-modules, then every direct summand has this property. Irving Kaplansky originally proved the theorem in this form . From this it follows, for example, that every projective module is the direct sum of countably generated modules. Therefore , if one wants to prove structure theorems via projective modules , one can, thanks to Kaplansky, limit oneself to countably generated ones. Every projective module is a direct summand in a free module. ${\displaystyle M}$

The decomposition theorem by Krull-Remak-Schmidt-Azmaya

Be two decompositions of . Are the endomorphism rings of all local and all are indivisible, so there is a bijection with for all . ${\displaystyle M=\oplus _{i\in I}M_{i}\cong \oplus _{j\in J}N_{j}}$ ${\displaystyle M}$ ${\displaystyle M_{i}}$ ${\displaystyle N_{j}}$ ${\displaystyle \alpha \colon I\rightarrow J}$ ${\displaystyle M_{i}\cong N_{\alpha (i)}}$ ${\displaystyle i\in I}$

This sentence generalizes many important sentences. For example:

• Every two bases of a vector space have the same thickness.
• The decomposition of a semi-simple module into a direct sum of simple modules is clear in the sense of the sentence.
• The decomposition theorem of Krull-Remak-Schmidt theorem for modules of finite length.

Individual evidence

1. ^ Friedrich Kasch modules and rings . Teubner, Stuttgart 1977, page 77 ISBN 3-519-02211-7
2. ↑ Robert Wisbauer, basics of module - and ring theory , publishing Reinhard Fischer, Munich 1988 Page 112 ISBN 3-88927-044-1
3. ↑ Frank W. Anderson, Kent R. Fuller, Rings and Categories of modules Springe, New York Berlin Heidelberg, 1992, page 106, ISBN 0-387-97845-3
4. ^ Friedrich Kasch modules and rings . Teubner, Stuttgart 1977, page 127 ISBN 3-519-02211-7

literature

• Frank W. Anderson and Kent R. Fuller: Rings and Categories of Modules . Springer, New-York 1992, ISBN 0-387-97845-3
• Friedrich Kasch: modules and rings . Teubner, Stuttgart 1977, ISBN 3-519-02211-7
• Robert Wisbauer: Fundamentals of module and ring theory. Reinhard Fischer, Munich 1988, ISBN 3-88927-044-1