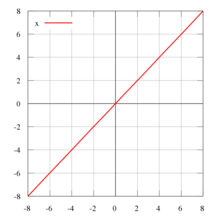
Identical figure
An identical mapping or identity in mathematics is a function that returns exactly its argument. Although both the identical map and the identity equation are often abbreviated to “identity”, they are different things.
definition
Let be a set , then the identical mapping to is defined by
that is, for each of true
The identical image is thus a bijection . The index is often omitted when the definition set is evident from the context. In this case there is also written instead . Instead of the notation , the notation is sometimes used , sometimes only or mainly in functional analysis .
The graph of the identical figure is the diagonal
properties
If there is any function, then the following applies to the composition (execution) with the identity:
and
Hence, in the set of all functions from to, identity is the neutral element with regard to the composition. Thus these functions form a monoid . In particular, identity is the neutral element in the group of permutations of the set .
The identity on the set of natural numbers is a multiplicative function that is considered in number theory .
In a topological space , identity is a continuous function . On a topological vector space , for example a Banach space , the identity is a continuous linear operator called the unity operator. If the Banach space is also finite dimensional , the identity is compact .
The matrix multiplication with the identity matrix (neutral element) is an identity mapping. In linear algebra , base change matrices can be understood as representation matrices of the identical mapping with respect to two different bases .
The existence of identities is an integral part of the definition of the category . In the best-known cases, these are the identical images, but in category theory the identities can also be more abstract objects. But even then the designations or are used and the linking rules mentioned above apply.
See also
Individual evidence
- ↑ Oliver Deiser: Introduction to set theory. Springer, 2004, ISBN 978-3-540-20401-5 , p. 59.