Irrational number

${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$

${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$stands for the set of irrational numbers

The number is irrational. ${\displaystyle {\sqrt {2}}}$

The number ( Pi ) is one of the best-known mathematical constants . ${\displaystyle \pi }$

An irrational number is a real number that is not a rational number . The characteristic of an irrational number is that it cannot be represented as the quotient of two whole numbers . In decimal notation , irrational numbers are represented with a non-periodic, infinite number of decimal places (e.g. 0.10110111011110…), i. that is, they are infinite non-periodic decimal fractions .

Well-known irrational numbers are Euler's number and the circle number , which are also transcendent . The square root of two and the division ratio of the golden section are also irrational numbers. ${\displaystyle {\rm {e}}}$ ${\displaystyle \pi }$ ${\displaystyle {\sqrt {2}}}$

definition

A real number is called irrational if it cannot be represented as a fraction of two whole numbers ; it cannot be written as with . ${\displaystyle {\tfrac {p}{q}}}$ ${\displaystyle p,q\in \mathbb {Z} }$

In contrast to rational numbers , which can be represented as finite or periodic decimal numbers , irrational numbers are those whose decimal representation neither breaks off nor is periodic.

There are two types of irrational numbers:

• Algebraic numbers , for example, or square roots of non- square numbers such as ${\displaystyle 1+{\sqrt[{3}]{5}}}$ ${\displaystyle {\sqrt {2}}}$
• Transcendent numbers , such as the circle number or Euler's number ${\displaystyle \pi =3{,}14159\ldots }$ ${\displaystyle {\rm {e=2{,}71828\ldots }}}$

The set of irrational numbers can be written as a difference set , where the set of real numbers and the set of rational numbers denote. ${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$

Discovery of irrationality

The first evidence of irrational proportions was in ancient Greece in the 5th century BC. With the Pythagoreans . Definitions for irrational numbers that meet today's demands for accuracy can already be found in the Elements of Euclid . Translations into today's language of mathematics were first given by Karl Weierstrass and Richard Dedekind .

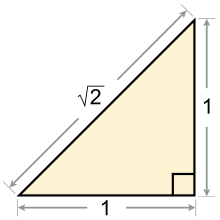
If you have a square with side length and calculates the diagonal , it follows from the Pythagorean theorem so . The positive solution to this equation is known today as . For Greek mathematicians, the question arose whether the length of this diagonal can be represented exactly by a ratio of two natural numbers and , that is, a fraction . A proof by contradiction, which is now taught in the school, handed down to us from Euclid. It is not known whether the discovery of irrationality occurred through the application of the Pythagorean theorem on a square or, as Kurt von Fritz said, through continuous division on the pentagram . ${\displaystyle 1}$ ${\displaystyle d}$ ${\displaystyle d^{2}=1^{2}+1^{2},}$ ${\displaystyle d^{2}=2}$ ${\displaystyle {\sqrt {2}}}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p/q}$

Older research in the history of science assumed that the discovery of irrationality led to a fundamental crisis in Greek mathematics or Pythagorean number theory. That is to say, one had previously assumed the basic premise that everything could be expressed by integer ratios, and the refutation of this view had shaken the Pythagorean worldview. An ancient legend was associated with this, according to which the Pythagorean Hippasus of Metapontium in the 5th century BC. BC committed a betrayal of secrets through the written announcement of this discovery and later drowned in the sea, which was interpreted as divine punishment. Some of the sources say that Hippasus himself discovered irrationality. Science historians today assume that there was no such crisis and that irrationality was not considered a secret. One possible explanation for the treacherous legend is that it came about through a misunderstanding, because the Greek adjective, which was used for "irrational" (in the mathematical sense), had the meanings "unspeakable" and "secret" at the same time. But it is also a fact that Greek mathematics changed fundamentally in the period after Hippasus.

Numbers whose irrationality has been proven

• The Pythagorean Archytas of Taranto already proved the irrationality of for natural numbers . The proof for the case ( ) is handed down in Euclid's elements ( Euclid's proof of the irrationality of the root of 2 ). Euclid himself generalized Archytas' theorem in his music theory, in which he proved the irrationality of any roots . ${\displaystyle {\sqrt {\tfrac {m+1}{m}}}}$ ${\displaystyle m}$ ${\displaystyle m=1}$ ${\displaystyle {\sqrt {2}}}$ ${\displaystyle {\sqrt[{n}]{\tfrac {m+1}{m}}}}$
• Another important quadratic irrationality is the golden ratio . ${\displaystyle \textstyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}$
• The Euler number is irrational. This has Leonhard Euler in 1737 proved . Their transcendence was proven by Charles Hermite in 1873 . ${\displaystyle \textstyle {\rm {e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}}}$
• In 1761 Johann Heinrich Lambert proved the irrationality of the circle number , its transcendence was proven in 1882 by Ferdinand von Lindemann . ${\displaystyle \pi }$
• The non-integer zeros of a normalized polynomial with integer coefficients are irrational. In particular, the square roots of non-square numbers are irrational. ${\displaystyle x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{0}}$ ${\displaystyle {\sqrt {2}},{\sqrt {3}},{\sqrt {5}},{\sqrt {6}},\dotsc }$
• In 1979 Roger Apéry proved the irrationality of the Apéry constant . ${\displaystyle \textstyle \zeta (3)=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}}$
• ${\displaystyle {\rm {e^{\pi }}}}$is transcendent (see Gelfond-Schneider theorem ).
• ${\displaystyle 2^{\sqrt {2}}}$is transcendent, as Carl Ludwig Siegel has proven.
• The transcendence of (as well as of ) follows from Gelfond-Schneider's theorem . ${\displaystyle {\sqrt {2}}^{\sqrt {2}}}$ ${\displaystyle 2^{\sqrt {2}}}$
• The lemniscatic constant is transcendent ( Theodor Schneider , 1937). ${\displaystyle \varpi =2{,}622057\ldots }$
• In 1963 Solomon W. Golomb proved the irrationality of the sum of the reciprocal of all Fermat numbers . The following applies:

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{F_{n}}}=\sum _{n=0}^{\infty }{\frac {1}{2^{2^{n}}+1}}\approx 0{,}59606317211782167942379392586279}$(Follow A051158 in OEIS )

Numbers presumed to be irrational

The irrationality of the sum of and is suspected but has not yet been proven. For not a single pair of whole, of different numbers and it is known whether is irrational. However, it is known that in the case of the existence of rational linear combinations, the value assumes a constant value. ${\displaystyle \pi }$ ${\displaystyle e}$ ${\displaystyle 0}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle m\cdot \pi +n\cdot {\rm {e}}}$ ${\displaystyle m/n}$

Proof of the irrationality of was presented in 2017. ${\displaystyle \pi \cdot {\rm {e}}}$

Furthermore, it is unknown whether , , , , , the Catalan's constant or Euler's constant are irrational. However, it makes sense to suspect so. ${\displaystyle 2^{\rm {e}}}$ ${\displaystyle \pi ^{\rm {e}}}$ ${\displaystyle \pi ^{\sqrt {2}}}$ ${\displaystyle \pi ^{\pi }}$ ${\displaystyle {\rm {e^{\rm {e}}}}}$ ${\displaystyle G=0,91596\ldots }$ ${\displaystyle \gamma =0{,}5772\ldots }$

The uncountability of irrational numbers

As Cantor's first diagonal argument shows, the set of rational numbers is countable . So there is a sequence of rational numbers that contains every rational number. Cantor's second diagonal argument proves that there are uncountably many real numbers. This also means that there must be an uncountable number of irrational numbers; because otherwise the real numbers would themselves be countable as the union of two countable sets.

Cantor has further shown that the set of algebraic numbers , to which all root expressions belong, can still be counted. In addition, the algebraic envelope of every countable subset of real or complex numbers (such sets can consist of transcendent numbers in particular) is also countable, i.e. it certainly does not contain all real numbers.

literature

• Tom Müller: Proof of irrationality. Heldermann Verlag, Lemgo 2014, ISBN 978-3-88538-125-9 .

Web links

Commons : Irrational Numbers  - collection of images, videos, and audio files

Individual evidence

1. ↑ There is no specific abbreviation for the set of irrational numbers, but a number is irrational if and only if it is real and not rational. The following applies:
   Set of irrational numbers: = set of real numbers without a set of rational numbers.
2. ↑ Lucio Russo: The forgotten revolution or the rebirth of ancient knowledge. Springer, Berlin / Heidelberg / New York 2005, ISBN 978-3-540-20938-6 , pp. 53-56.
3. ^ Walter Burkert: Wisdom and Science. Studies on Pythagoras, Philolaus and Plato. Carl, Nürnberg 1962, pp. 430-440.
4. ^ Walter Burkert: Wisdom and Science. Studies on Pythagoras, Philolaus and Plato. Carl, Nuremberg 1962, p. 436 f.
5. ^ Solomon W. Golomb : On the sum of the reciprocals of the Fermat numbers and related irrationalities. Canad. J. Math. , Vol. 15 , 1963, pp. 475-478 , archived from the original on March 21, 2016 ; accessed on August 9, 2016 . 
6. ^ Nelson A. Carella: The Product eπ Is Irrational. (PDF; 214 kB) In: arxiv.org. June 19, 2017, accessed February 1, 2019 . 
7. ↑ This means in particular that not all irrational numbers can be "represented" or "calculated".