Square number

16 balls form a square.

A square number is a number that is created by multiplying an integer by itself. For example, is a square number. The first square numbers are ${\displaystyle 144=12\cdot 12}$

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, ... (sequence A000290 in OEIS )

For some authors, the zero is not a square number, so that the sequence of numbers only starts with the one.

The term square number is derived from the geometric figure of the square . The number of stones that you need to lay a square is always a square number. For example, a square with side length 4 can be laid with the help of 16 stones.

Because of this relationship with a geometric figure, the square numbers count among the figured numbers , which also include the triangular numbers and cube numbers . These terms were already known to the ancient Greek mathematicians .

properties

A square number is exactly then an even number when its base is straight. ${\displaystyle a^{2}}$ ${\displaystyle a}$

Formulas for generating square numbers

Each square number is the sum of the first odd natural numbers . ${\displaystyle n^{2}}$ ${\displaystyle n}$

${\displaystyle {\begin{aligned}&1&=1&=1^{2}\\&1+3&=4&=2^{2}\\&1+3+5&=9&=3^{2}\\&1+3+5+7&=16&=4^{2}\\&&\vdots &\end{aligned}}}$

This law, also known as the odd number theorem in English literature , is illustrated by the following figures.

${\displaystyle 0+\color {blue}1\color {black}=1}$	${\displaystyle 1+\color {blue}3\color {black}=4}$	${\displaystyle 4+\color {blue}5\color {black}=9}$	${\displaystyle 9+\color {blue}7\color {black}=16}$

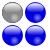
From left to right, the first four square numbers are represented by the corresponding number of balls. The blue balls each show the difference to the previous square number. Since there is always a row and a column from left to right, the number of blue balls increases by 2. Starting with the 1 on the far left, the blue balls run through all the odd numbers.

The Education Act

${\displaystyle \forall n\in \mathbb {N} \colon n^{2}=\sum _{i=1}^{n}(2i-1)=1+3+5+\dotsb +(2n-1)}$

can be proven inductively . The beginning of induction

${\displaystyle 1^{2}=\sum _{i=1}^{n}(2i-1)}$

follows from the obvious and ${\displaystyle 1^{2}=1}$

${\displaystyle \sum _{i=1}^{1}(2i-1)=2\cdot 1-1=1.}$

From the induction hypothesis

${\displaystyle n^{2}=\sum _{i=1}^{n}(2i-1)}$

follows because of the binomial formula and ${\displaystyle (n+1)^{2}=n^{2}+2n+1}$

${\displaystyle \sum _{i=1}^{n+1}(2i-1)=\sum _{i=1}^{n}(2i-1)+2(n+1)-1=\sum _{i=1}^{n}(2i-1)+2n+1}$

immediately the induction claim

${\displaystyle (n+1)^{2}=\sum _{i=1}^{n+1}(2i-1).}$

In addition, each square number is twice the sum of the first natural numbers plus the number , for example: ${\displaystyle n^{2}}$ ${\displaystyle n-1}$ ${\displaystyle 2\cdot {\tfrac {(n-1)\cdot n}{2}}=n^{2}-n}$ ${\displaystyle n}$

${\displaystyle {\begin{aligned}&1&=1&=1^{2}\\&2\cdot 1+2&=4&=2^{2}\\&2\cdot (1+2)+3&=9&=3^{2}\\&2\cdot (1+2+3)+4&=16&=4^{2}\\&&\vdots &\end{aligned}}}$

This can also be easily illustrated geometrically: In the square made up of spheres, there are spheres on one of the diagonals , each on this side and on the other side of it . ${\displaystyle n^{2}}$ ${\displaystyle n}$ ${\displaystyle 1+2+3+\dotsb +(n-1)}$

Trick to calculate the square of a number with one digit 5

The square of numbers that end in 5 (which can be represented in the form of a natural number ) can easily be calculated in your head. You multiply the number without the units digit 5 ​​(e.g. 6 for 65) by its successor (here 6 + 1 = 7) and append the digits 2 and 5 to the product (here 6 7 = 42) (final result 4225). ${\displaystyle 10\cdot k+5}$ ${\displaystyle k}$

${\displaystyle {\underline {1}}5^{2}={\underline {2}}25}$

${\displaystyle {\underline {2}}5^{2}={\underline {6}}25}$

${\displaystyle {\underline {3}}5^{2}={\underline {12}}25}$

${\displaystyle {\underline {4}}5^{2}=[4\cdot (4+1)]25={\underline {20}}25}$

${\displaystyle [a]5^{2}=[a\cdot (a+1)]25}$

Proof: ${\displaystyle (10\cdot k+5)^{2}=100k^{2}+100k+25=k(k+1)\cdot 10^{2}+25}$

Relationships to other figured numbers

Triangular numbers

10 + 15 = 25

Each square number can be represented as the sum of two consecutive triangular numbers. The adjacent picture shows an example of how the square number 25 results as the sum of the triangular numbers and . ${\displaystyle \Delta _{4}=10}$ ${\displaystyle \Delta _{5}=15}$

This phenomenon can also be described by a formula.

${\displaystyle {\begin{aligned}n^{2}&={\frac {n(n-1)}{2}}+{\frac {(n+1)n}{2}}\\&=\Delta _{n-1}+\Delta _{n}\\\end{aligned}}}$

Centered square numbers

In addition to the pattern on which the square numbers are based, there is a second pattern for laying a square. Additional squares are placed around a stone in the middle of the square. The number of stones required for this pattern corresponds to a centered square number . Each centered square number is the sum of two consecutive square numbers, as can be seen from their geometric pattern.

The term for centered square numbers can be rearranged with the help of the binomial formula so that the two square numbers become visible: ${\displaystyle 2n^{2}+2n+1}$ ${\displaystyle (n+1)^{2}=n^{2}+2n+1}$

${\displaystyle {\begin{aligned}2n^{2}+2n+1&=n^{2}+(n^{2}+2n+1)\\&=n^{2}+(n+1)^{2}\end{aligned}}}$

Pyramid numbers

The sum of the first square numbers results in the -th pyramid number : ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle \sum _{i=1}^{n}i^{2}=1^{2}+2^{2}+3^{2}+\dotsb +n^{2}={\frac {n(n+1)(2n+1)}{6}}}$

The following figure illustrates this relationship using the example of the fourth pyramid number.

End digits of square numbers

Square numbers never end with one of the digits 2, 3, 7 or 8, because no square of a single-digit number ends with one of these digits.

If the last digit is any number , then applies to its square ${\displaystyle y}$ ${\displaystyle a=10\cdot x+y}$

${\displaystyle a^{2}=100\cdot x^{2}+20\cdot xy+y^{2}.}$

The last digit of is therefore identical to the last digit of . However, among the ten squares 0, 1, 4, 9, 16, 25, 36, 49, 64 and 81 of all digits, there is none that ends in 2, 3, 7 or 8. ${\displaystyle a^{2}}$ ${\displaystyle y^{2}}$

Residual classes of square numbers

The previous statement about possible final digits of square numbers means that 0, 1, 4, 5, 6, 9 represent the possible remainder classes of the square numbers modulo 10. For other numbers , too , the remainder classes of the square numbers are always only a part of the total possible remainder classes. For example, the possible remainder classes of the squares are 0, 1, 3, 4, 5 and 9. In particular, 0, 1 are the remainder classes of both squares modulo 3 and modulo 4, and 0, 1, 4 are the remainder classes of squares modulo 8 From this it follows, for example, that 3 is not a residual class of the sum of two square numbers modulo 4, and that 7 is not a residual class of the sum of three square numbers modulo 8. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n=11}$

In elementary number theory studies play on quadratic residues important.

Number of divisors

Only square numbers have an odd number of factors . Proof: Be , and . It is because . contains all factors of , so the number of factors of is equal . Is a square number, then is . Otherwise is . ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle A=\{d\in \mathbb {N} \mid d^{2}\leq n,d|n\}}$ ${\displaystyle B=\{d\in \mathbb {N} \mid n\leq d^{2},d|n\}}$ ${\displaystyle |A|=|B|}$ ${\displaystyle \textstyle B=\{{\frac {n}{d}}\mid d\in A\}}$ ${\displaystyle A\cup B}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle |A\cup B|=|A|+|B|-|A\cap B|=2|A|-|A\cap B|}$ ${\displaystyle n}$ ${\displaystyle A\cap B=\{{\sqrt {n}}\}}$ ${\displaystyle A\cap B=\emptyset }$

Series of reciprocals

→ Main article : Basel problem

The sum of the reciprocal values ​​of all squares is

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\dotsb ={\frac {\pi ^{2}}{6}}}$.

For a long time it was not known whether this series would converge, and if so, to what limit. It was not until 1735 that Leonhard Euler found the value of the series.

Sums of two consecutive square numbers

With the triangular number the identity applies: . ${\displaystyle n^{2}+(n+1)^{2}=4\cdot \Delta _{n}+1}$

Sums of consecutive square numbers

There are some strange relationships for the sum of consecutive squares:

${\displaystyle {\begin{aligned}3^{2}+4^{2}&=5^{2}\\10^{2}+11^{2}+12^{2}&=13^{2}+14^{2}\\21^{2}+22^{2}+23^{2}+24^{2}&=25^{2}+26^{2}+27^{2}\\36^{2}+37^{2}+38^{2}+39^{2}+40^{2}&=41^{2}+42^{2}+43^{2}+44^{2}\end{aligned}}}$

or in general

${\displaystyle \sum _{k=2n^{2}+n}^{2n^{2}+2n}k^{2}=\sum _{k=2n^{2}+2n+1}^{2n^{2}+3n}k^{2}={\frac {n(n+1)(2n+1)}{6}}\cdot (12n^{2}+12n+1)}$

Some prime numbers can be written as the sum of two, three or even six consecutive squares (other numbers of summands are not possible):

• n = 2:

${\displaystyle 1^{2}+2^{2}=5}$

${\displaystyle 2^{2}+3^{2}=13}$

${\displaystyle 4^{2}+5^{2}=41}$

${\displaystyle \vdots }$

(Episode A027861 in OEIS , episode A027862 in OEIS )

• n = 3:

${\displaystyle 2^{2}+3^{2}+4^{2}=29}$

${\displaystyle 6^{2}+7^{2}+8^{2}=149}$

${\displaystyle 12^{2}+13^{2}+14^{2}=509}$

${\displaystyle \vdots }$

(Episode A027863 in OEIS , episode A027864 in OEIS )

• n = 6:

${\displaystyle 2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+7^{2}=139}$

${\displaystyle 3^{2}+4^{2}+5^{2}+6^{2}+7^{2}+8^{2}=199}$

${\displaystyle 4^{2}+5^{2}+6^{2}+7^{2}+8^{2}+9^{2}=271}$

${\displaystyle \vdots }$

(Episode A027866 in OEIS , episode A027867 in OEIS )

See also

• Four squares set

Web links

Commons : Square numbers  - collection of pictures, videos and audio files

Wiktionary: square number  - explanations of meanings, word origins, synonyms, translations

Individual evidence

1. ^ Helmuth Gericke : Mathematics in Antiquity, Orient and Occident. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1 , pp. 142-143.
2. ↑ Eric W. Weisstein : Odd Number Theorem . In: MathWorld (English).