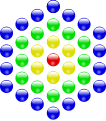
Figured number

Figure numbers are classes of numbers that relate to geometric figures . If you place regular pieces from pieces and count the pieces, you get figured numbers. Examples of figured numbers are the square numbers , cube numbers, and pyramid numbers .

The sequences of figured numbers form so-called arithmetic sequences . To determine the explicit formula, one examines the differences between neighboring sequential members, which in turn form a sequence, the sequence of differences . If no other possibility is evident, the explicit regularity of each arithmetic sequence can be determined algebraically with the so-called polynomial approach.

The Greek mathematicians were already concerned with figured numbers.

Polygonal numbers

Depending on the structure, a distinction is made between decentralized and centered polygonal numbers, whereby the former are usually only called polygonal numbers. The term polygonal number is also used as an umbrella term for decentralized and centered polygonal numbers.

(Decentralized) polygonal numbers

See main article: Polygonal Number

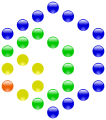
A polygonal number is a number for which there is a polygon (polygon) that can be laid with a corresponding number of stones. For example, 16 is a polygonal number, as a square can be made up of 16 stones.

• 

  The 10 is the fourth triangular number .

• 

  The 16 is the fourth square number .

• 

  The 22 is the fourth pentagonal number .

• 

  The 28 is the fourth hexagonal number .

For all prime numbers p> 5 there is an n-th k-polygonal number with , but none and at least one with the triangular number . For the larger prime twin p '> 5 applies exclusively . ${\displaystyle P_{k}^{(2)}(n),n\geq 3,k\geq 3}$ ${\displaystyle p-1=P_{k}^{(2)}(n)}$ ${\displaystyle p+1=P_{k}^{(2)}(n),n\geq 4,k\geq 3}$ ${\displaystyle 2\leq r<p-2,p-2=r{\pmod {P_{3}^{(2)}(r)}}}$ ${\displaystyle P_{3}^{(2)}(r)}$ ${\displaystyle p'-2=2{\pmod {P_{3}^{(2)}(2)}}}$

Centered polygonal numbers

See main article: Centered Polygonal Number

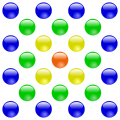
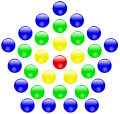
Another laying pattern for regular polygons starts with a stone in the middle. Several polygons are placed around this, with their side lengths increasing by one from the inside to the outside. The number of stones required for this corresponds to a centered polygon number. The following pictures show some examples:

• 

  The 19 is the fourth centered triangular number .

• 

  The 25 is the fourth centered square number .

• 

  The 31 is the fourth centered pentagonal number .

• 

  The 37 is the fourth centered hexagon number .

Rectangular numbers or pronic numbers

Twelve spheres form a rectangle.

See main article: Rectangular Number

A square or pronic number is the product of two consecutive natural numbers . For example, is a rectangle number. If you place stones in a rectangle , one side of which is 1 longer than the second, the number of stones corresponds to a number of the rectangle. ${\displaystyle 12=3\cdot 4}$

Three-dimensional body

The geometric constructions for the polygonal numbers can be expanded from flat figures to three-dimensional bodies . This is how pyramidal numbers and other types of figured numbers are created. Since the figures are polyhedra , some authors use the term polyhedron for this .

Pyramidal numbers or pyramidal numbers

See main article: Pyramidal Number

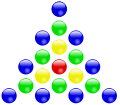
Adding the first square numbers gives the -th quadratic pyramidal number . Geometrically, this means stacking several squares to form a pyramid . The following picture shows this for the fourth quadratic pyramidal number. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle Pyr_{4}(n)}$

This construction principle can be transferred from square numbers to any polygonal numbers. This creates the different classes of pyramidal numbers.

Sums of centered polygonal numbers

Octahedral numbers

The octahedron numbers can be interpreted as the sum of the first centered square numbers:

${\displaystyle Okt_{n}=\sum _{i=1}^{n}ZQ_{i}=ZQ_{1}+ZQ_{2}+\ldots +ZQ_{n}=Pyr_{4}(n)+Pyr_{4}(n-1)=n+4T_{n-1}}$

The first octahedron numbers are

0, 1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891, 1156, ... (sequence A005900 in OEIS ).

Cube numbers

The (decentralized) cube numbers are the sum of the first centered hexagonal numbers . The direct calculation formula is:

${\displaystyle Kub_{n}=n^{3}}$

Centered cube numbers

Centered cube numbers can be defined analogously as

${\displaystyle ZK_{n}=Kub_{n}+Kub_{n-1}=n^{3}+(n-1)^{3}=2n^{3}-3n^{2}+3n-1}$.

Rhombic dodecahedral numbers

The rhombic dodecahedron numbers can be assembled to form a rhombic dodecahedron . You have the shape

${\displaystyle ZK_{n}+6\cdot Pyr_{4}(n)=(2n-1)(2n^{2}-2n+1)}$.

The first numbers of this form are

0, 1, 15, 65, 175, 369, 671, ... (sequence A005917 in OEIS ).

Regular figured numbers

Figure numbers can be defined for any dimensions . In general, the -th figured number is the order with the binomial coefficient ${\displaystyle n}$ ${\displaystyle r}$

${\displaystyle f_{r}^{n}={n+r-1 \choose r}={\frac {(n+r-1)(n+r-2)\ldots n}{1\cdot 2\cdot \ldots \cdot r}}}$

identical.

With increasing order arise from the triangular numbers

${\displaystyle f_{2}^{n}=\Delta _{n}=1+2+\ldots +n}$

the tetrahedral numbers

${\displaystyle f_{3}^{n}=T_{n}=\Delta _{1}+\Delta _{2}+\ldots +\Delta _{n}}$,

and pentatope numbers

${\displaystyle f_{4}^{n}=P_{n}=T_{1}+T_{2}+\ldots +T_{n}}$,

This sequence can be continued recursively in any dimensions:

${\displaystyle f_{r+1}^{n}=\sum _{i=1}^{n}f_{r}^{i}=f_{r}^{1}+f_{r}^{2}+\ldots +f_{r}^{n}}$

Figure numbers erected over the sides of the Pythagorean k triangle

Generalized, the Pythagorean theorem establishes squares with the area (the square numbers n² as an integer) over the sides of a Pythagorean k triangle (for the term, see sequence A198453 in OEIS ). For certain integer Pythagorean k-triples (a, b, c) with the triangle ABC is right-angled according to the cosine theorem and the difference angle to the right angle over the longest side is thus zero, whereby the limit value of the natural numbers assumes (infinity axiom). ${\displaystyle k=0}$ ${\displaystyle n\cdot (n+0)=n^{2}}$ ${\displaystyle a^{2}+b^{2}=c^{2}}$ ${\displaystyle \phi }$ ${\displaystyle csc(\phi )=(a+b+c+0)/0=\infty }$

Set of rectangles (6,3,7)

Triangle set (2,2,3)

In this case , right-angled triangles of the surface (the triangular numbers Δ _{n in} whole numbers ) are erected with the small or large cathetus over the sides of the triangle ABC. For certain integer Pythagorean triples (a, b, c) with the triangle ABC is obtuse / acute angled, but that of the difference angle to the right angle over the longest side is an integer (sequence A012132 in OEIS ). ${\displaystyle k=\pm 1}$ ${\displaystyle 1/2\cdot n\cdot (n+1)=T(n)}$ ${\displaystyle \pm 1}$ ${\displaystyle T(a)+T(b)=T(c)}$ ${\displaystyle csc(\phi )=(a+b+c+1)/1}$

In this case , special 2-rectangles of the area (the 2-rectangle numbers R _{n as} an integer ) are erected with the small and large sides of the rectangle above the sides of the triangle ABC. For certain integer Pythagorean triples (a, b, c) with the triangle ABC with an even circumference is obtuse / acute angled, but that of the difference angle to the right angle over the longest side is an integer (sequence A198457 in OEIS ). ${\displaystyle k=\pm 2}$ ${\displaystyle n\cdot (n+2)=R(n)}$ ${\displaystyle \pm 2}$ ${\displaystyle R(a)+R(b)=R(c)}$ ${\displaystyle csc(\phi )=(a+b+c+2)/2}$

In cases or , the cosine law therefore provides special information on divisibility. In general, in the border transition of the triangular circumference towards infinity, the difference angle converges towards zero and thus the shape of the Pythagorean k triangle ABC to a (0-) Pythagorean triangle ABC (sequence A103606 in OEIS ). ${\displaystyle k=\pm 1}$ ${\displaystyle k=\pm 2}$ ${\displaystyle a+b+c}$ ${\displaystyle \phi }$

literature

• John H. Conway , Richard K. Guy : Number Magic. Of natural and imaginary and other numbers. Birkhäuser, Basel a. a. 1997, ISBN 3-7643-5244-2 .
• Lancelot Hogben : Mathematics for Everyone. An introduction to the science of numbers and figures. Newly revised edition. Pawlak, Herrsching 1985, ISBN 3-88199-208-1 , p. 151.
• Elena Deza, Michel Marie Deza: Figurate Numbers. World Scientific. Singapore 2012, ISBN 978-981-4355-48-3 .
• John H. Conway, Richard Guy: The Book of Numbers . Springer, 1996, ISBN 978-0-387-97993-9
• Jochen Ziegenbalg: figured numbers . Springer, 2018, ISBN 978-3-658-20934-6

Web links

Commons : Figurative Numbers  - Collection of images, videos, and audio files

• Eric W. Weisstein : Figurate Number . In: MathWorld (English).
• Jutta Gut: Page about figured numbers

Individual evidence

1. ↑ Eric W. Weisstein : Rhombic Dodecahedral Number . In: MathWorld (English).
2. ^ Leonard Eugene Dickson : History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0 , p. 7