Centered polygonal number

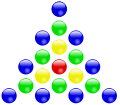
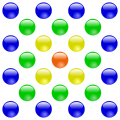
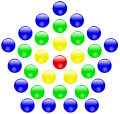
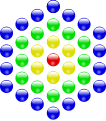
A centered polygonal number is a number to which a regular polygon (polygon) can be placed in a certain pattern and with a corresponding number of stones. The laying pattern starts with a single stone in the center of the polygon. Further polygons are placed around this center stone, with their side lengths increasing by one from the inside to the outside. Depending on the number of sides, one speaks, for example, of centered triangular numbers , centered square numbers , centered pentagonal numbers , centered hexagonal numbers , and so on. Because of their relationship to a geometric figure , the centered polygonal numbers belong to the class of figured numbers . Another way to trace numbers back to polygons is the (decentralized) polygonal numbers .

Examples

• 

  The 19 is the fourth centered triangular number.

• 

  The 25 is the fourth centered square number.

• 

  The 31 is the fourth centered pentagonal number.

• 

  The 37 is the fourth centered hexagon number.

calculation

Derivation of the formula: The hexagon for the fifth centered hexagon number is divided into six equilateral triangles with side length 4, leaving the circle in the middle.

The -th centered corner number is calculated according to the formula ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle 1+{\frac {kn(n-1)}{2}}}$.

Alternatively, the -th centered corner number can also be used with the -th triangular number according to the formula ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle (n-1)}$ ${\displaystyle \Delta _{n-1}}$

${\displaystyle 1+k\cdot \Delta _{n-1}}$

to calculate.

In addition to a clear explanation, the formula can also be proven algebraically. According to the stated principle of formation, the drawing of corners with the side length increasing by one around a starting point, the -th corner number can be passed through ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle 1+\sum _{i=2}^{n}{(k\cdot (i-1))}}$

express.

${\displaystyle {\begin{aligned}PZ_{n}&=1+\sum _{i=2}^{n}{(k\cdot (i-1))}\\&=1+(k\cdot 1+k\cdot 2+\dotsb +k\cdot (n-1))\\&=1+k(1+2+\dotsb +(n-1))\\&=1+k\cdot {\frac {n(n-1)}{2}}\\&=1+k\cdot \Delta _{n-1}\end{aligned}}}$.

literature

• Lancelot Hogben : Mathematics for Everyone. An introduction to the science of numbers and figures. Newly revised edition. Pawlak, Herrsching 1985, ISBN 3-88199-208-1 , p. 151ff.