Polygonal number

A polygonal number is a number for which there is a regular polygon (polygon) that can be laid with a corresponding number of stones. For example, 16 is a polygonal number, as a square can be made up of 16 stones. The polygonal numbers include triangular and square numbers .

The polygonal numbers are among the figured numbers . Another way to trace numbers back to polygons is to use the centered polygonal numbers .

The polygonal numbers can be generated by a simple calculation rule. You choose a natural number as the difference. The first number is always 1, and all subsequent polygonal numbers are created by adding the difference to the previous one. The following examples show this. ${\ displaystyle d}$

Triangular numbers: The difference 1 leads to the sums from which the triangular numbers are obtained. ${\ displaystyle 1 + 2 + 3 + 4 + \ ldots}$ ${\ displaystyle 1,3,6,10, \ ldots}$
Square numbers: The difference 2 leads to the sums from which the square numbers are obtained. ${\ displaystyle 1 + 3 + 5 + 7 + \ ldots}$ ${\ displaystyle 1,4,9,16, \ ldots}$
Pentagonal numbers: The difference 3 leads to the sums from which the pentagonal numbers are obtained. ${\ displaystyle 1 + 4 + 7 + 10 + \ ldots}$ ${\ displaystyle 1,5,12,22, \ ldots}$
Hexagonal numbers: The difference 4 leads to the sums from which the hexagonal numbers are obtained. ${\ displaystyle 1 + 5 + 9 + 13 + \ ldots}$ ${\ displaystyle 1,6,15,28, \ ldots}$

The individual summands are each the elements of an arithmetic sequence with the initial element 1 and the respective difference (cf. sequence of differences ). This structure of the polygonal numbers is also reflected in the corresponding polygons:

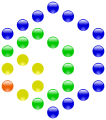
The 10 is the fourth triangular number .
The 16 is the fourth square number .
The 22 is the fourth pentagonal number .
The 28 is the fourth hexagonal number .

Occasionally this is also defined as the zeroth triangular number, square number, etc. According to this convention, the sequence of triangular numbers is for example . ${\ displaystyle 0}$ ${\ displaystyle 0,1,3,6,10, \ ldots}$

calculation

The respective -th corner number can be calculated with the formula ${\ displaystyle n}$ ${\ displaystyle k}$

{\ displaystyle {(k-2) n ^ {2} - (k-4) n \ over 2} = (k-2) {\ binom {n} {2}} + n}

to calculate.

If there is any corner number, the corresponding one is calculated using the formula ${\ displaystyle k}$ ${\ displaystyle x}$ ${\ displaystyle n}$

{\ displaystyle n = {\ frac {{\ sqrt {8 (k-2) x + (k-4) ^ {2}}} + k-4} {2 (k-2)}}.}

Derivation

Let be the number of pages. The -te corner number, with , is formed by adding a point to pages. The extended pages have points in common. The -th corner number thus has points more than the -th corner number. The -th corner number is therefore: ${\ displaystyle k \ in \ mathbb {N}}$ ${\ displaystyle n}$ ${\ displaystyle k}$ ${\ displaystyle n \ in \ mathbb {N}}$ ${\ displaystyle k-2}$ ${\ displaystyle (k-2) -1}$ ${\ displaystyle (n + 1)}$ ${\ displaystyle k}$ ${\ displaystyle (n + 1) (k-2) - (k-3)}$ ${\ displaystyle n}$ ${\ displaystyle k}$ ${\ displaystyle n}$ ${\ displaystyle k}$

{\ displaystyle (1 \ cdot (k-2) - (k-3)) + (2 \ cdot (k-2) - (k-3)) + \ ldots + (n \ cdot (k-2) - (k-3))}

{\ displaystyle = \ sum \ limits _ {i = 1} ^ {n} ((k-2) \ cdot i- (k-3))}

{\ displaystyle = -n \ cdot (k-3) + \ sum \ limits _ {i = 1} ^ {n} (k-2) \ cdot i}

{\ displaystyle = -n (k-3) + (k-2) \ sum \ limits _ {i = 1} ^ {n} i}

{\ displaystyle {\ stackrel {\ mathrm {I.}} {=}} - n (k-3) + (k-2) \ cdot {\ tfrac {1} {2}} n (n + 1)}

{\ displaystyle = {\ tfrac {1} {2}} [- 2nk + 6n + k (n (n + 1)) - 2n (n + 1)]}

{\ displaystyle = {\ tfrac {1} {2}} \ left [-2nk + 6n + kn ^ {2} + nk-2n ^ {2} -2n \ right]}

{\ displaystyle = {\ tfrac {1} {2}} \ left [-nk + 4n-2n ^ {2} + kn ^ {2} \ right]}

{\ displaystyle = {\ tfrac {1} {2}} \ left [(k-2) n ^ {2} - (k-4) n \ right]}

{\ displaystyle = {\ frac {(k-2) n ^ {2} - (k-4) n} {2}}}

to : Application of the Gaussian empirical formula ${\ displaystyle \ mathrm {I.}}$

This formula also remains valid for a (flat, degenerate to an empty double line) two-triangle with its validity, ${\ displaystyle k = 2}$

{\ displaystyle = {\ frac {(2-2) n ^ {2} - (2-4) n} {2}} = n}

The "two-sided numbers" calculated with it correspond exactly to the natural numbers , that is to say the sum of the rows of arithmetic stones in a row . ${\ displaystyle 1,2,3,4, \ ldots}$ ${\ displaystyle n}$ ${\ displaystyle n}$

Sum of the reciprocal values

The sum of the reciprocal values of all corner numbers is convergent. The following applies: ${\ displaystyle k}$ ${\ displaystyle k> 2}$

{\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {2} {(k-2) n ^ {2} - (k-4) n}} = {\ dfrac {-2 \ psi ({\ frac {2} {k-2}}) - 2 \ gamma} {k-4}}}

(with : Euler-Mascheroni constant and : Digamma function )

{\ displaystyle \ gamma}

{\ displaystyle \ psi (x)}

Applications

According to Fermat's theorem of polygonal numbers, each number can be represented as a sum of at most - corner numbers. ${\ displaystyle k}$ ${\ displaystyle k}$

literature

James Mitchell (Ed.): A Dictionary of the Mathematical and Physical Sciences, according to the latest Improvements and Discoveries. G. & WS Whittaker, London 1823, archive.org .
Constance Reid : From Zero to Infinity. What Makes Numbers Interesting. 4th edition. Mathematical Association of America , Washington DC 1992, ISBN 0-88385-505-4 , Chapter 5, books.google.de
Lawrence Downey, Boon W. Ong, James A. Sellers: Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers . math.psu.edu (PDF; 93 kB).

Web links

Eric W. Weisstein : Polygonal Number . In: MathWorld (English).
Polygonal number at PlanetMath (English)

Individual evidence

↑ See article by Downey, Ong, Sellers.

[1] See article by Downey, Ong, Sellers.