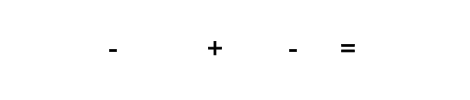Triangular number

A triangle made out of ten stones

A triangle number is a number that is the sum of all numbers from 1 up to an upper limit . For example, the 10 is a triangular number, there is. The first triangular numbers are: ${\displaystyle n}$ ${\displaystyle 1+2+3+4=10}$

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ... (sequence A000217 in OEIS )

For some authors, the zero is not a triangular number, so the sequence of numbers only starts with the one.

The name triangle number is derived from the geometric figure of the triangle . The number of stones that you need to lay an equilateral triangle always corresponds to a triangle number. For example, a triangle can be made from ten stones, each side of which is formed by four stones.

Because of this relationship with a geometric figure, the triangular numbers are among the figured numbers , which also include the square numbers and cube numbers . Pythagoras already dealt with triangular numbers.

calculation

The -th triangular number is the sum of the numbers from 1 to . ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle {\begin{aligned}\Delta _{1}&=1&=&\ 1\\\Delta _{2}&=1+2&=&\ 3\\\Delta _{3}&=1+2+3&=&\ 6\\\Delta _{4}&=1+2+3+4&=&\ 10\\&\qquad \vdots &\end{aligned}}}$

Instead of adding up the individual numbers, triangular numbers can also be calculated using the Gaussian sum formula :

${\displaystyle \Delta _{n}={\frac {n\cdot (n+1)}{2}}}$

The right side is identical to the binomial coefficient over 2: ${\displaystyle n+1}$

${\displaystyle \Delta _{n}={n+1 \choose 2}}$

This formula can be illustrated by interpreting the triangle number. The triangle number can be interpreted as a triangle or stairs. Double the number of a triangle corresponds to two identical stairs that can be joined together to form a rectangle.

This rectangle is balls high and balls wide and therefore contains balls. A triangle number corresponds to half of the balls, which results in the above formula for triangle numbers. ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle n\cdot (n+1)}$

properties

• All triangular numbers > 3 are composite numbers .
• The sum of the first n cube numbers is equal to the square of the n th triangular number [example: 1 + 8 + 27 + 64 = 100 = 10 ² ]
• The difference between the squares of two consecutive triangular numbers results in a cube number.
  This can be derived from the property above. Since the square of the nth triangular number is formed from the sum of the first n cube numbers and the square of the (n + 1) th triangular number is formed from the sum of the first n + 1 cube numbers, the difference must be the (n + 1) -th cube number come out.
• Eight times a triangular number added with 1 always results in an odd square number: ${\displaystyle 8\cdot \Delta _{n}+1=(2n+1)^{2}}$

7th	9

• Every even perfect number is also a triangular number:
  According to Leonhard Euler , an even perfect number can be represented by the formula , whereby a prime number ( Mersenne prime number ) must be. If the formula with 2 extends and by substituted, one arrives at the formula representing a triangle figure: ${\displaystyle (2^{n}-1)\cdot 2^{n-1}}$ ${\displaystyle 2^{n}-1\ }$ ${\displaystyle (2^{n}-1)\cdot 2^{n-1}}$ ${\displaystyle 2^{n}\ }$ ${\displaystyle m\ }$

${\displaystyle (2^{n}-1)\cdot 2^{n-1}={\frac {(2^{n}-1)\cdot 2^{n-1}\cdot 2}{2}}={\frac {(2^{n}-1)\cdot 2^{n}}{2}}={\frac {(m-1)\cdot m}{2}}}$

• The sum of two triangular numbers is not congruent 5 (mod 9).
• ${\displaystyle \Delta _{n}\equiv \{1,n/2+2\}\mod {n+2}}$when . ${\displaystyle n=\{ungerade,gerade\}}$
• The following applies: ${\displaystyle \Delta _{n+1}=(2n+1)+\Delta _{n-1}.}$
• The nth triangular number is equal to the difference between the nth centered hexagon number and the nth centered octagon number:

${\displaystyle \Delta _{n}=(1+3n)\cdot (2+3n)/2-(1+2n)^{2}}$. This identity (with the nth in each case) is the minimal solution of a countably infinite number of solutions (see here ).

Sum of three triangular numbers

Pierre de Fermat suggested that every natural number can be represented as the sum of a maximum of three triangular numbers. This assumption was proven by Carl Friedrich Gauß , who wrote in his diary on July 10, 1796:

EYPHKA num = Δ + Δ + Δ.

The more general statement is known as Fermat's polygon theorem.

Relationships to Square Numbers

Sum of two consecutive triangular numbers

10 + 15 = 25

The sum of two consecutive triangular numbers results in a square number. The adjacent picture shows an example of how the triangular numbers and the square number 25 add up. ${\displaystyle \Delta _{4}=10}$ ${\displaystyle \Delta _{5}=15}$

This phenomenon can also be described by a formula.

${\displaystyle {\begin{aligned}\Delta _{n-1}+\Delta _{n}&={\frac {n(n-1)}{2}}+{\frac {(n+1)n}{2}}\\&=n^{2}\end{aligned}}}$

For another explanation of this phenomenon is decomposed the triangular number in the sum of and the previous triangular number : . The following applies accordingly ${\displaystyle {\frac {n\cdot (n+1)}{2}}}$ ${\displaystyle n}$ ${\displaystyle {\frac {(n-1)\cdot n}{2}}}$ ${\displaystyle 2\cdot {\frac {(n-1)\cdot n}{2}}+n=(n-1)\cdot n+n=n^{2}-n+n=n^{2}}$

The fact that two consecutive triangular numbers add up to a square number was already written down in the 2nd century by the Greek mathematician Theon von Smyrna in his work “The usefulness of mathematical knowledge for reading Plato's”.

Alternating sum of square numbers

If you take the square number and subtract and add the smaller square numbers alternately, you get the -th triangular number as the result . For example, the fourth and fifth triangular numbers are calculated as follows: ${\displaystyle n^{2}}$ ${\displaystyle n}$

${\displaystyle 16-9+4-1=10=\Delta _{4}}$

${\displaystyle 25-16+9-4+1=15=\Delta _{5}}$

By making use of the fact that every square number is the sum of two consecutive triangular numbers, one can explain this relationship using its geometric illustration.

You can see that (with the exception of the largest) each triangle appears exactly twice in the sum: once with plus and once with minus. As a result, the small triangles cancel each other out, and all that remains is the large triangle.

With the help of the mathematical vocabulary, the above facts can be reproduced very briefly: The -th triangular number is the alternating sum of the square numbers from to 1. The corresponding mathematical formula is ${\displaystyle n}$ ${\displaystyle n^{2}}$

${\displaystyle \Delta _{n}=\sum _{i=1}^{n}(-1)^{n+i}\cdot i^{2}}$

Square triangular numbers

Square-triangular numbers are triangular numbers that are also square numbers. The first square triangle numbers are

0, 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, ... sequence A001110 in OEIS

These are the triangular numbers with the indices

0, 1, 8, 49, 288, 1681, 9800, 57121, ... sequence A001108 in OEIS

In order for a triangular number to be a square number, this number must be

${\displaystyle {\frac {n\cdot (n+1)}{2}}}$

The following apply: Of the two numbers and , one of the two must be an odd square number, while the other must be twice a square number. Because the two consecutive numbers are always prime; in particular, one of the two is always odd and the other is even. The even number is therefore twice a square number, and the odd number is itself an (odd) square number. ${\displaystyle n+1\ }$ ${\displaystyle n\ }$

Triangular numbers and centered polygonal numbers

Centered polygonal numbers are related to regular polygons , which are laid out according to the following pattern: A single stone lies in the center of the polygon. Further polygons are placed around this stone, with their side lengths increasing by one from the inside to the outside.

These patterns can also be laid according to another rule. Again start with the single stone in the middle. But in the second step, triangles are placed around the center for the -th centered -Neck number according to the pattern of the -th triangular number. The following picture shows this for the first through fourth centered square number . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle (n-1)}$

This results in the following formula for the -th centered corner number: ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle 1+k\cdot \Delta _{n-1}=1+{\frac {kn(n-1)}{2}}}$

The sum of three consecutive triangle numbers is a centered triangle number. Since module 3 has the cycle (1,0,0) for triangular numbers, every centered triangular number is equivalent to 1 (mod 3).

Palindromes of numbers under the triangular numbers

There are several palindromes of numbers among the triangular numbers . examples are

1, 3, 6, 55, 66, 171, 595, 666, 3003, 5995, 8778, ... (sequence A003098 in OEIS )

Among these are the 11th, 1,111th, 111,111th and 11,111,111th triangular numbers. Charles Trigg found this out for the 1,111th and 111,111th triangular numbers .

Series of reciprocals

The sum of the reciprocal values ​​of all triangular numbers is

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{\Delta _{n}}}={\frac {2}{1\cdot 2}}+{\frac {2}{2\cdot 3}}+{\frac {2}{3\cdot 4}}+\dots =2}$

Solution according to Gottfried Wilhelm Leibniz , with , ${\displaystyle {\frac {1}{\Delta _{n}}}={\frac {2}{n(n+1)}}={\frac {2(n+1)-2n}{n(n+1)}}={\frac {2}{n}}-{\frac {2}{n+1}}}$

${\displaystyle {\begin{aligned}1/\Delta _{1}&={\tfrac {1}{1}}&={\tfrac {2}{1}}\color {Red}-{\tfrac {2}{2}}\\1/\Delta _{2}&={\tfrac {1}{3}}&=\color {Red}{\tfrac {2}{2}}-{\tfrac {2}{3}}\\1/\Delta _{3}&={\tfrac {1}{6}}&=\color {Red}{\tfrac {2}{3}}-\color {Red}{\tfrac {2}{4}}\\1/\Delta _{4}&={\tfrac {1}{10}}&=\color {Red}{\tfrac {2}{4}}-\color {Red}{\tfrac {2}{5}}\\1/\Delta _{5}&={\tfrac {1}{15}}&=\color {Red}{\tfrac {2}{5}}-\color {Red}{\tfrac {2}{6}}\\1/\Delta _{6}&={\tfrac {1}{21}}&=\color {Red}{\tfrac {2}{6}}-\color {Red}{\tfrac {2}{7}}\\&\qquad \vdots &\qquad \vdots \end{aligned}}}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{\Delta _{n}}}={\frac {1}{1}}+{\frac {1}{3}}+{\frac {1}{6}}+{\frac {1}{10}}+{\frac {1}{15}}+{\frac {1}{21}}+\dots =2}$

Triangle root

Analogous to the square root for the square number, the side length of a triangular number x can also be determined with the triangular root n :

${\displaystyle n={\frac {{\sqrt {8x+1}}-1}{2}}.}$

So z. B. the triangular number x = 10 formed from n = 4 rows.

The Cantor pairing function can be reversed with the help of the triangle root.

Miscellaneous

Irene Schramm-Biermann, Visible Mathematics series. Visualization of triangular numbers and their calculation using the Gaussian sum formula

• The tenth, hundredth, thousandth, ten thousandth etc. triangular number is 55, 5,050, 500,500, 50,005,000 etc. ( OEIS , A037156 ).

In general ${\displaystyle \Delta _{10^{n}}={\frac {10^{2n}+10^{n}}{2}}=5\cdot (10^{2n-1}+10^{n-1}).}$

• The triangular sequences split into two partial sequences. The terms of the sequence 3, 10, 21, 36, 55, 78,… ( OEIS , A014105 ) can be formed using the formula (see also Sophie-Germain prime number ). For the other half, the hexagonal numbers 1, 6, 15, 28, 45, 66, ... (OEIS, A000384 ), the formation rule applies . ${\displaystyle n\cdot (2n+1)}$ ${\displaystyle n\cdot (2n-1)}$
• The Puerto Rican mathematician Pedro Antonio Pizá found the relationship in 1950

${\displaystyle 3\cdot \left(\sum _{k=1}^{n}\Delta _{k}\right)^{3}=\sum _{k=1}^{n}\Delta _{k}^{3}+2\cdot \sum _{k=1}^{n}\Delta _{k}^{4}={\frac {1}{72}}n^{3}(n+1)^{3}(n+2)^{3}}$

between sums and powers of triangular numbers.

• The number of diagonals in the convex corner is . ${\displaystyle n}$ ${\displaystyle \Delta _{n-2}-1={\frac {n(n-3)}{2}}}$
• The sequence of central polygonal numbers (also known as the lazy waiter's sequence of numbers) is obtained by adding the number 1 to each of the triangular numbers.
• For the Floor function applies: . ${\displaystyle \lfloor 2{\sqrt {\Delta _{n}}}\rfloor =\lfloor (n+{\frac {1}{2}}){\sqrt {2}}\rfloor }$
• The remainder of the module is alternating in n: if n is {odd, even} and r is odd, but if r is even. ${\displaystyle T(n)\equiv \{(r+1)/2+\lfloor {r^{2}/2}\rfloor ,T(r+1)\}\mod {n+r},0\leq (r-1)^{2}+1\leq n}$ ${\displaystyle T(n)\equiv \{T(r+1),r/2+\lfloor {r^{2}/2}\rfloor \}\mod {n+r},0\leq (r-1)^{2}+1\leq n}$
• 

  Visualization for triples (2,2,3)
  For all , but only for certain triples with applies (OEIS, A012132 ); for obtuse triangles (a, b, c) applies :; for acute-angled triangles (a + 1, b + 1, c + 1) where: . This also applies to real lines ,, e.g. integer: (-1, -1, -1), (-2, -1, 1), (-1, 1, 1), (2, 2, 3), since these lines are the elements of a Hilbert space . ${\displaystyle a>1}$ ${\displaystyle (a,b,c)}$ ${\displaystyle 1<a\leq b<c}$ ${\displaystyle \Delta _{a}+\Delta _{b}=\Delta _{c}}$ ${\displaystyle \csc(\phi )=1+a+b+c=-{\frac {2ab}{a^{2}+b^{2}-c^{2}}}}$ ${\displaystyle \csc(\phi )=(-1)+(a+1)+(b+1)+(c+1)={\frac {2(a+1)(b+1)}{(a+1)^{2}+(b+1)^{2}-(c+1)^{2}}}}$ ${\displaystyle a(a+1)+b(b+1)=c(c+1),a+b-c\neq 0}$

Generalizations

see main article: polygonal number , regular figured number

There are essentially two generalizations of triangular numbers. If you stay in the plane, you can apply the construction principle of triangular numbers to polygons with more corners. This creates the polygonal numbers, which include, for example, the square numbers and the pentagonal numbers .

The second generalization is to leave the plane and move on to higher dimensions. In three dimensions, one then looks at a tetrahedron , which is a pyramid with equilateral triangles as sides. In the four-dimensional one arrives at the pentatope , the sides of which are tetrahedra. This can be continued at will. The corresponding figured numbers are called tetrahedral numbers , pentatopic numbers and, in general, regular figured numbers. In the one-dimensional, the natural numbers should also be mentioned.

For triangular numbers , the formation rule applies to exactly one of three disjoint number classes (sequence A111774 in OEIS ) ${\displaystyle \Delta _{n}\geq 6}$

${\displaystyle \Delta _{n}={\frac {n\cdot (n+2k-1)}{2}};k\geq 1,n\geq 3}$

for the special case . ${\displaystyle k=1}$

See also

• Pascal's triangle
• Centered triangle number
• Metcalfe's law

literature

• John H. Conway , Richard K. Guy : The Book of Numbers. Copernicus, New York NY 1996, ISBN 0-387-97993-X .

Web links

Commons : Triangle Numbers  - collection of images, videos, and audio files

Individual evidence

1. ^ Leonard Eugene Dickson : History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0 , p. 1.
2. ↑ Hubert Mania: Gauss. A biography. Rowohlt, Reinbek bei Hamburg 2008, ISBN 978-3-498-04506-7 , p. 108.
3. ^ Leonard Eugene Dickson: History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0 , p. 2
4. ↑ Pedro Antonio Pizá: Sums of Powers of triangular numbers. In: Scripta Mathematica 16 (1950), p. 127.