Real power
The real power is the electrical power that is available for conversion into other powers (e.g. mechanical, thermal or chemical). It must be distinguished from the reactive power that cannot be used for this conversion.
The effective power is given in the unit watt . With constant voltage and constant current , the active power is the product of voltage and current :
With variable values and the real power is the equivalent of the instantaneous power :
For periodic voltages and currents, averaging over a period with the period duration:
Specifications for sinusoidal alternating voltage
The electrical power supply network or three-phase alternating current network is an important application . Only this is dealt with here. The voltage has a sinusoidal curve over time; Voltage and current are alternating quantities with the same fundamental frequency . In this case there are stipulations in DIN 40108 and DIN 40110 that must be observed for this article.
Active power with sinusoidal current
Representation with time functions
The sinusoidal course of the current only occurs if there are only linear consumers in the network. With ohmic loads, voltage and current are in phase. When capacitive or inductive loads occur, there is also a shift in the phase angle between the course of current and voltage. With the effective values of voltage and current , the amplitudes and , the phase shift angle and the angular frequency is
By applying the trigonometric relationship
follows
and with the use of the rms values
The expression contains
- a time-independent summand, the real power , and
- a summand oscillating with twice the frequency and the amplitude , the mean value of which is equal to zero. The size is called the apparent power .
This results in the sinusoidal curve
The component of the current that is decisive for the active power is called the active current .
Complex representation
In electrical engineering, it is customary to carry out the alternating current calculation (i.e. calculating with sinusoidal alternating quantities) with the help of pointers in the complex plane , since this is much simpler than the calculation with trigonometric functions . To connect the power quantities to the complex AC calculation, the complex apparent power is defined, which combines active and reactive power in a complex quantity. It is calculated from the product of the complex rms value of the voltage with the conjugate complex rms value of the current.
The apparent power , i.e. the amount of the complex apparent power , is the Pythagorean sum of active and reactive power. The real power is the real part , the reactive power the imaginary part of the complex apparent power.
Sign questions
The conventions on counting directions of the voltages and currents by means of generator and consumer arrows mean that the active power is positive for the flow of energy from the generator to the consumer. The picture of the time course shown above also shows negative values of ; then energy is fed back. The real power is thereby smaller than the apparent power; but it remains positive.
In networks with several sources and loads, the direction of the energy flow between network sections cannot only reverse for a fraction of a period. In terms of power, this is described by reversing the sign of the real power, so that values can also make sense.
Active power with non-sinusoidal current
If the voltage is sinusoidal but the current is not, the equation remains valid with the restriction that and are parameters of the fundamental oscillation of the current. Harmonics are not included.
Measurements in the energy supply network
Measuring device
A power meter has a current path and a voltage path . It multiplies instantaneous values of voltage and current strength, averages over the instantaneous values of the product and is therefore an active power meter according to the definition of active power. The electromechanical measuring mechanism suitable for this has been replaced by electronic measuring transducers .
Every measuring device has a measuring range that must not be exceeded because otherwise no error limit is guaranteed. In addition, the power meter includes nominal values of voltage and current which, according to the manufacturer's instructions, may only be exceeded to a small extent, otherwise the device will be damaged. This type of overload can definitely occur without exceeding the measuring range!
For the measurement with the correct sign, it is important to ensure that the paths are correctly connected, which are specified by correct circuit diagrams. As a rule , within this article, in accordance with DIN 43807, the following is consistently observed in the circuit diagrams:
The arrows shown in the following circuit diagrams point to the correct sign
- for the current in the current path from left to right
- for the voltage on the voltage path from bottom to top.
(Some voltage arrows are not shown in the circuit diagrams; how they should indicate is nevertheless clear according to the system.)
If this results in a negative measured value, but no negative value can be output, a deliberate reversal of the direction on the voltage path (or current path) helps.
The terminals on the input side of laboratory devices are often marked with an asterisk; Devices for permanent installation are numbered according to DIN 43807; See picture for examples.
Every power meter has its own consumption
- in the current path due to a voltage drop (as with the ammeter ),
- in the voltage path through a current consumption (as with the voltmeter ).
With the real measuring device, a distinction must be made between the active power of the producer and the consumer.
Single-phase network
There are two ways to connect the power meter, see the corresponding picture. However, none of the circuits records the active power of the producer or consumer, but is measured
- in the upper circuit generator voltage times consumer current,
- In the lower circuit, the consumer voltage times the generator current.
In the upper circuit, which is preferably used, the costs of the energy consumption of the measuring device are borne
- as far as coming from the voltage path by the generator,
- as far as coming from the current path by the consumer.
Three-phase network
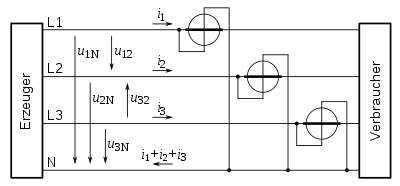
Four-wire circuit with neutral wire
The most comprehensive case is the four-wire circuit with a neutral conductor and three outer conductors, as is common in the low-voltage network with = 230 V or = 400 V, in connection with any load. Arbitrary means here: Currents with different amplitudes and different phase shifts with respect to the respective reference voltage can flow in the three outer conductors. Then
This can be measured with three power meters or a combination device.
Three-wire circuit
Due to the lack of a neutral conductor in the three-wire circuit
- .
With
and
becomes
where the last summand is zero, which means that it vanishes. In a three-wire circuit with any load, two power meters are sufficient if they are operated in an Aron circuit according to the next equation.
With
and ,
where = angle between and
and = angle between and
Notes on this:
- Formally, a conductor, here in accordance with DIN 43807, conductor L2, can be understood as a return conductor.
- and have no descriptive meaning, not even in the sign. For example, with a pure reactive load , but .
- Because you have to pay attention to whether the power meter, which is designed for the voltage , can also handle the higher voltage . If the voltage is reduced by the factor using a series resistor or a voltage transformer , this risk of overload is eliminated. Because of the reduced voltage, however, the measured value has to be increased by the factor .
Symmetrical loading
With symmetrical loading, it is sufficient to use only one power meter for the power consumption through one of the outer conductors. The total output is three times that.
- .
In a three-wire circuit, the neutral conductor potential must be artificially created using a star point as shown in the picture with two resistors that are just as large as the resistance of the voltage path in the power meter.
Further designations
| designation | size | application |
|---|---|---|
| Power factor | general | |
| Displacement factor | for sinus quantities | |
| Active factor | for sinus quantities | |
| Blind factor | for sinus quantities | |
| Loss factor | with sine values for capacitors and coils |
All information is in accordance with DIN 40110-1: 1994.
See also
literature
- Wilfried Weißgerber: Electrical engineering for engineers 2: AC technology, locus curves, transformers, multi-phase systems. Springer Vieweg, 9th edition. 2015
- Moeller / Frohne / Locher / Müller: Fundamentals of electrical engineering. Teubner, 18th edition 1996
- Kurt Bergmann: Electrical measurement technology: Electrical and electronic processes, plants and systems. Vieweg, 5th ed. 1993
- and almost every other textbook on electrical engineering or electrical measurement technology
Individual evidence
- ↑ DIN 40108: 2003-06 Electricity systems: terms, sizes, symbols
- ↑ DIN 40110-1: 1994-03 AC quantities : two-wire circuits
- ↑ DIN 43807: 1983-10 measuring, controlling, regulating; Electrical measuring devices; Terminal designations for panel measuring devices, built-in measuring devices and measuring transducers for measuring power and power factor
















![\ sin \ alpha \ cdot \ sin \ beta = {\ tfrac 12} [\ cos (\ alpha - \ beta) - \ cos (\ alpha + \ beta)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c6640c64031b0851face35a320dfcbec718308d)
![p = {\ tfrac 12} \ {\ hat u} \; {\ hat \ imath} \ [\ cos \ varphi - \ cos (2 \ omega t- \ varphi)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de505c04c53917db367b4a28c97f4094fcb1cc5c)