Inductance

This article describes electrical inductance. Regarding the component inductance and hydraulic inductance ; see inductance (component) and hydraulic inductance .

Physical size
Surname	Electrical inductance
Formula symbol	${\displaystyle L}$
Size and unit system unit dimension SI H M · L 2 · T −2 · I −2 cgs cm −1 s 2 L −1 · T 2 esE ( cgs ) cm −1 s 2 L −1 · T 2 emE ( cgs ) fromH L.

Inductance is a property of electrical circuits or components , especially coils . A distinction must be made between self-inductance (also called self-inductance or self-induction ) and mutual inductance ; “Inductance” without an addition almost always means self-inductance. The self-inductance of a circuit relates the rate of change of the electrical current over time to the electrical voltage : ${\displaystyle i(t)}$ ${\displaystyle u(t)}$

${\displaystyle u(t)=L{\frac {\mathrm {d} i(t)}{\mathrm {d} t}}}$.

The symbol for self-inductance is . It was chosen in honor of Emil Lenz , whose theoretical work on electromagnetic induction was fundamental. The unit of measurement for self-inductance in the SI system of units is Henry , named after the American physicist Joseph Henry . ${\displaystyle L}$

In the important case of a wire loop or coil, the relationship between voltage and time-varying current can be understood directly using Ampère's law and induction law : an electric current generates a magnetic field , as described by Ampère's law . The change in the magnetic field over time, as described by the law of induction, “induces” an electrical voltage in the same circuit. Both effects are proportional to the number of turns , the self-inductance of a coil is therefore proportional to . ${\displaystyle N}$ ${\displaystyle N^{2}}$

Changes in current in one circuit also induce voltages in other circuits in the vicinity . This "mutual induction" or mutual induction is described with the coefficients of mutual inductance. ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle L_{mn}=L_{nm}}$

Self and mutual induction and the corresponding inductances play an important role in transformers , electric motors and electronics .

Scope

The first requirement for the validity of the equation is that the magnetic field is generated “quasi-statically” by the electric current . There must be no phase differences between magnetic field and current and no emission of electromagnetic waves , i. that is, the frequencies must be sufficiently small. ${\displaystyle u=L{\frac {\mathrm {d} i}{\mathrm {d} t}}}$

Furthermore, the power distribution must be frequency-independent. This is the case at low frequencies at which the current density is constant across the conductor cross-section, as well as at high frequencies at a complete skin effect , where the current flows in the conductor surface (as in superconductors ). At frequencies with a partial skin effect, the inductance is frequency-dependent. In the case of thin conductors, however, it makes little difference whether the current flows in the conductor cross-section or in the conductor surface - the frequency dependence is small.

Finally, it is also assumed that magnetizable materials located in the area of ​​the magnetic fields have constant permeability numbers . Otherwise there is a non-linear inductance .

In this context, however, the relationship applies to conductor loops with conductors of any length , and the inductances are determined solely by the arrangement and expansion of the electrical conductors and magnetizable materials. ${\displaystyle u=L{\frac {\mathrm {d} i}{\mathrm {d} t}}}$

Induction in electrical engineering, unit of measure

Animation of a direct current circuit: After closing the button, S ₁ lights up immediately, while the brightness of S ₂ increases only gradually due to the self-induction of the coil L counteracting the flow of current.
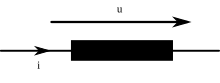
After opening the button, the self-induction of the coil L causes it to temporarily take over the role of the voltage source. In the circuit formed by L, S ₂ and S ₁ , the current through S _{2 is} retained for a short time, while the current through S ₁ changes direction. Both lamps lose their brightness equally until they go out.

Current flow through lamps S ₁ and S ₂ and the voltage U ₂ applied to coil L over time. The fine, inclined straight lines illustrate the time constants ₁ and ₂ . ${\displaystyle \tau }$ ${\displaystyle \tau }$

For conductor loops, the inductance is in electrical often defined by the included by the conductor loop interlinked magnetic flux in accordance with ${\displaystyle \Psi }$

${\displaystyle L={\frac {\Psi }{I}}\,}$.

If the conductor covers the same magnetic flux several times, e.g. B. all turns of a coil with the same size, there is a special case and self-inductance for the chained magnetic flux ${\displaystyle \Phi }$ ${\displaystyle N}$ ${\displaystyle N\Phi }$

${\displaystyle L={\frac {N\cdot \Phi }{I}}\,}$.

If only magnetic substances with a constant permeability number are present in the vicinity of the circuit, then it follows from the law of flux that the magnetic flux density is proportional to the current in a conductor loop. Therefore, the total magnetic flux generated by the current is directly proportional to the instantaneous value of the current strength . The proportionality factor occurring in the case of windings is the self-inductance L. ${\displaystyle B}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle \Phi }$ ${\displaystyle i}$ ${\displaystyle N}$

${\displaystyle \Phi ={\frac {L\cdot I}{N}}\,}$.

An inductance of 1 H is present if a self-induced voltage of 1 volt is created along the conductor with a uniform current change of 1 ampere per second .

${\displaystyle 1\ \mathrm {H} =1{\frac {\mathrm {V} \cdot \mathrm {s} }{\mathrm {A} }}\,}$

However, if the magnetic substances such as iron in the vicinity of the electrical conductor do not have a constant permeability number μ _r (this depends , for example, on the magnetic flux density ), then the inductance is not a constant proportionality factor, but a function of the magnetic flux density. There is then a saturation magnetization . The resulting non-linear inductances are much more difficult to treat analytically. ${\displaystyle B}$ ${\displaystyle L(B)}$

If a non-linear inductance is controlled around an operating point , the change in the linked flux in relation to the change in the current can deviate from the value of the static inductance. For infinitesimally small changes around the operating point, the increase in the tangent to the curve results in the dynamic inductance ${\displaystyle \Psi }$ ${\displaystyle \Psi -I}$

${\displaystyle L_{\mathrm {dyn} }={\frac {\mathrm {d} \Psi }{\mathrm {d} I}}\,}$.

Obsolete unit

Until the middle of the 20th century, the inductance of coils was sometimes labeled with the unit cm or quadrant . This specification in centimeters comes from the fact that the inductance in the electromagnetic CGS system of units (EMU), which is practically hardly used today , was expressed in the length dimension. The name Quadrant comes from the fact that 10 ⁹ EMU is equal to 1 Henry, which in turn corresponds to the length in cm of an earth quadrant .

An inductance of 1 cm or 1 quadrant in electromagnetic CGS units corresponds to 1 nH in SI units.

Mathematical derivation

In accordance with the law of induction , the circulating voltage u _{i of} a loop at rest around the magnetic flux results from the rate of change of the magnetic flux passing through this loop or from the induced electric field strength E _i along the loop: ${\displaystyle \Phi }$ ${\displaystyle \Phi }$

${\displaystyle u_{i}=\oint {\vec {E}}_{i}\cdot \mathrm {d} {\vec {s}}=-{\frac {\mathrm {d} \Phi }{\mathrm {d} t}}\,}$.

If the conductor loop wraps around the magnetic flux N times, as is the case with a coil, for example , the following applies approximately:

${\displaystyle u_{i}=-N\cdot {\frac {\mathrm {d} \Phi }{\mathrm {d} t}}\,}$.

The negative sign that occurs corresponds to Lenz's rule : the induced voltage tries to produce a current that counteracts the original change in current. If current and voltage defined for the inductor as a passive component in the same direction, the result for u : . With the above definition of inductance, the relationship between the terminal voltage u as a function of the current i can be expressed as a differential equation : ${\displaystyle u_{i}}$ ${\displaystyle i}$ ${\displaystyle u}$ ${\displaystyle u=-u_{i}}$

${\displaystyle u={\frac {\mathrm {d} N\Phi }{\mathrm {d} t}}={\frac {\mathrm {d} \Psi }{\mathrm {d} t}}={\frac {\mathrm {d} (Li)}{\mathrm {d} t}}=L{\frac {\mathrm {d} i}{\mathrm {d} t}}+i{\frac {\mathrm {d} L}{\mathrm {d} t}}\,}$

In most cases the inductance does not change with time and the current-voltage relationship at the inductance can be specified too

${\displaystyle u=L{\frac {\mathrm {d} i}{\mathrm {d} t}}\,}$

The magnetic flux that occurs is the flux that is only generated due to the current i through the conductor loops. A change in this flux induces a voltage in each of the N conductor loops and thus becomes effective as a linked magnetic flux . In this case, further external magnetic fluxes through the conductor loops are assumed not to exist or are constant over time. The voltage u is called the terminal voltage that occurs during self-induction . ${\displaystyle \Phi }$ ${\displaystyle u=-u_{i}}$ ${\displaystyle \Psi }$

Consumer arrow system

The sign in the above equation depends on the counting direction of current and voltage. If the direction of the voltage u coincides with the direction of the current along the conductor loop, as shown in the adjacent graphic, we speak of the so-called consumer counting system , and the following applies:

${\displaystyle u_{L}\left(t\right)=L\cdot {\frac {\mathrm {d} i_{L}\left(t\right)}{\mathrm {d} t}}\,}$.

If the directions of voltage u current i along the conductor loop are oppositely directed, one speaks of the so-called generator counting arrow system , and the following applies:

${\displaystyle u_{L}\left(t\right)=-L\cdot {\frac {\mathrm {d} i_{L}\left(t\right)}{\mathrm {d} t}}\,}$.

This voltage drop u , which occurs when the current changes, is then called self- induction voltage or inductive voltage drop . The above differential equation is the element equation that can be used to describe linear inductances such as coils in electrical circuits.

Network model

Based on the law of induction, externally acting, time-variable magnetic fluxes in time-constant conductor loops generate time-variable electrical voltages. But the magnetic flux, which is created by a current through the coil itself, also acts on the coil. If the current intensity through the coil changes, the magnetic field generated by the coil itself changes and thereby induces a voltage in the coil itself which is opposite to the change in current intensity. This fact is commonly referred to as self-induction. The faster and stronger the magnetic field changes, the higher the induced voltage generated. In principle, self-induction can be fully described by the law of induction and does not require any formal additions or adjustments.

However, with the network theory common in electrical engineering, which is used, for example, to describe electrical machines such as transformers, there may be difficulties in understanding, because network theory does not know any field variables such as magnetic flux.

Self-induction effect, represented as a self-induced source voltage

Self-induction effect, shown as a network model with inductive voltage drop

Instead, voltages and currents that vary over time are used in equivalent circuit diagrams with passive components such as coils and electrical resistors . The induced voltages are modeled as voltage sources, which are historically also referred to as electromotive force (EMF) . Since induced voltages are not a force in the physical sense, the term EMF should be avoided to avoid misunderstandings and should be referred to as self-induced source voltage .

In the network model, as shown, among other things, in circuit diagrams , counting arrows and certain orientations are used, as shown in the adjacent figure. For clarification, the external magnetic flux Φ _ext acting on the conductor loop and the induced voltages u _ext caused by it are provided with the index ext . Under load, the external closed loop current flowing i generates a magnetic flux Φ _I , which with the index I is features. The self-induced source voltage can be modeled as a voltage source with the amount u _i , as shown in the first figure, and is opposite to the voltage u _ext driving the coil current i . It is therefore also referred to as counter-voltage . This representation is used, for example, in the description of the so-called magnetizing current in a transformer.

The model of the inductive voltage drop , as shown in the second figure, does not require an additional voltage source. The voltage occurring at the drawn coil L points in the same direction as the current i which is caused by the externally driving voltage u _ext . This representation has the advantage that the relationships in the network model in the case of harmonic processes can be described more easily using Ohm's law with reactances . The important in electrical special case of harmonic processes in the occurring sizes reduces the time derivatives in the law of induction on multiplications by jω (dΦ / d t ≡ jωΦ), resulting in the complex plane corresponds to a rotation through 90 ° and access to complex alternating current calculation represents . It denotes the imaginary unit . ${\displaystyle \mathrm {j} }$

Inductive reactance

Transforming the differential equation:

${\displaystyle u(t)=L\cdot {\frac {\mathrm {d} i(t)}{\mathrm {d} t}}\,}$

into the Laplace domain with the independent variable , (Fourier, ), the differential operator becomes the factor , and we have: ${\displaystyle s=\sigma +\mathrm {j} \omega =\mathrm {j} \omega }$ ${\displaystyle \sigma =0}$ ${\displaystyle {\mathrm {d} }/{\mathrm {d} t}}$ ${\displaystyle \mathrm {j} \omega }$

${\displaystyle U(\mathrm {j} \omega )=\mathrm {j} \omega L\cdot I(\mathrm {j} \omega )\,}$.

The symbol indicates the angular frequency . Similar to Ohm's law, an alternating current resistance can be derived from this for the coil: ${\displaystyle \omega }$ ${\displaystyle \omega =2\pi f}$

${\displaystyle {\underline {Z}}={\frac {{\underline {U}}(\mathrm {j} \omega )}{{\underline {I}}(\mathrm {j} \omega )}}=\mathrm {j} \omega L\,}$

define, which is also known as (complex) impedance .

Will, e.g. B. For very simple circuits that do not consider the phase shift between current and voltage at the inductance, AC calculations can also be carried out without complex numbers. If an inductance is connected to an alternating voltage of the magnitude U , the magnitude I of the current can be calculated using the formula:

${\displaystyle I={\frac {U}{X_{L}}}\,}$

The following applies to the inductive reactance X _L at the frequency f :

${\displaystyle X_{L}=\omega \cdot L=2\pi f\cdot L\,}$.

• Voltage and current curve
• 

  Air core coil

• 

  Coil with iron core

However, this only applies to inductances that have a constant permeability number that is not dependent on the modulation, as is the case, for example, with an air-core coil .

The no-load current from air-core coils can be less than 90 degrees out of phase with the voltage. At the low frequency of 50 Hz in the example measurement, the ohmic resistance is dominant. Due to its hysteresis curve, the no-load current of coils with an iron core is completely different from that of an air core coil.

Application of self-induction

Self-induction is used, among other things, to generate the required high ignition voltage for fluorescent lamps or for spark plugs in gasoline engines . Voltages of a few 1000 V can be generated. In this way, high-voltage pulses are generated in the electric fence and the spark inductor .

Switching any inductance is a burden for switches. The resulting high voltage is dangerous for switches, especially electronic switches such as transistors , because when switching off the magnetic field changes very abruptly and thus generates the high self-induction voltage. In order to avoid destroying the switch or to limit the voltage, a capacitor or a free-wheeling diode is connected in antiparallel to the coil.

The self-induction is, among other things, the reason for the inductance, which is required to describe the behavior of the coil in alternating current circuits. The inductance leads to a phase shift between current and voltage, which is used in the context of the complex AC calculation when calculating inductive resistances .

Determination of inductivity of various conductor arrangements

By using the calculation methods for magnetic fields, in particular the Biot-Savart law , the external inductances can be determined analytically for some simple geometric conductor arrangements. In the field calculation, more complicated conductor arrangements are usually only accessible by means of numerical calculation methods.

The conductor arrangements shown in more detail below also have technical significance: in the production of inductors (designation for electrical components with a defined inductance as the main property), such a standard shape is often used. Such components are called coils or chokes .

Inductance of a ring coil

Toroidal coil

A ring coil, also known as a toroidal coil , consists of a ring with a mean radius and cross-sectional area whose magnetic properties are decisive. It is often good magnetically conductive and has a high relative permeability , such as ferrite . What occurs is the magnetic field constant , a natural constant. ${\displaystyle r}$ ${\displaystyle A}$ ${\displaystyle \mu _{r}}$ ${\displaystyle \mu _{0}}$

This ring-shaped core is wound with a thin layer of wire with turns. The inductance is then given as an approximation: ${\displaystyle N}$ ${\displaystyle L}$

${\displaystyle L=N^{2}\cdot {\frac {\mu _{0}\mu _{r}A}{2\pi r}}\,}$.

A better approximation for the inductance of a ring coil, which takes into account the dependence of the magnetic field strength as a function of the radius, is:

${\displaystyle L=N^{2}\cdot {\frac {\mu _{0}\mu _{r}h}{2\pi }}\cdot \ln {\frac {R}{r}}\,}$.

A rectangular cross-section of the ring with the height is assumed. The outer radius of the core is marked with and the inner radius with . ${\displaystyle h}$ ${\displaystyle R}$ ${\displaystyle r}$

In all cases it is true that these equations only provide good approximate results if the ring is wound sufficiently thin.

The advantage of evenly wound toroidal coils lies in the freedom from fields outside the winding, which is why they do not emit magnetic interference fields and are hardly susceptible to such.

Inductance of a solenoid

Cylinder coil (air core coil)

In the case of a cylindrical air core coil , the length of which is greater than the diameter of the cross section , the inductance can be calculated approximately as follows: ${\displaystyle l}$ ${\displaystyle A}$

${\displaystyle L=N^{2}\cdot {\frac {\mu _{0}A}{l}}={\frac {N^{2}}{R_{m}}}\,}$.

In addition to the requirement of a thin-layer, closed wrapping, the magnetic resistance of the outer space is neglected and only the core is assumed. This equation is also only an approximation. For shorter cylinder coils there are approximation formulas that take into account the finite length of the coil and thus the “poorer” magnetic field guidance in its interior. For a coil with a length of at least 0.6 times the radius, the following applies ( : turn radius ): ${\displaystyle R_{m}}$ ${\displaystyle r_{w}}$

${\displaystyle L=N^{2}\cdot {\frac {\mu _{0}A}{l+2r_{w}/2{,}2}}\,}$.

If the solenoid is filled with a material, the external magnetic field space becomes relevant. The permeability number (for most materials ) has to be taken into account and the simple formulas above cannot be used. Such solenoids filled with a magnetic material and having an open magnetic circuit are often used and, despite the surrounding magnetic fields, have some advantages: due to the air in the magnetic circuit, they hardly ever reach magnetic saturation, are easy to manufacture and have a low intrinsic capacitance. ${\displaystyle \mu _{r}>1}$

Derivation of the approximation formula

From the relationship to the induction voltage when the magnetic flux inside a long coil changes ${\displaystyle \Phi =BA={\mu _{0}\mu _{r}NI \over l}A}$

${\displaystyle U_{\mathrm {ind} }(t)=-N{\dot {\Phi }}(t)}$

follows

${\displaystyle U_{\mathrm {ind} }=-{\mu _{0}\mu _{r}N^{2}A \over l}{\dot {I}}(t)}$

The inductance L is off

${\displaystyle U_{\mathrm {ind} }=-L{\dot {I}}(t)}$

identified with

${\displaystyle L={\mu _{0}\mu _{r}N^{2}A \over l}}$.

Determination of the inductance using the A _L value

In practice, ready-made coil cores are often used, for which the manufacturer often specifies an inductance constant A _L (Al value, usually in nH per square turn) and corresponds to the reciprocal value of the magnetic resistance R _m . In this value, all material constants and the special geometry of the arrangement are already summarized as an approximation. If you wind the core with N turns, you get a coil with the inductance:

${\displaystyle L=A_{L}\cdot N^{2}={\frac {1}{R_{m}}}\cdot N^{2}\,}$.

This only applies if the core material is operated in a linear range of its characteristic curve consisting of induction B and magnetic field strength H or remains below the saturation induction.

Field energy

Inductive components such as coils store energy in the form of their magnetic field. The magnetic field of a coil of inductance L , through which the instantaneous value of the current I flows, contains the energy W:

${\displaystyle W={\frac {1}{2}}\cdot L\cdot I^{2}\,}$

In the event of a sudden interruption in the circuit, the energy stored in the coil must be converted in a very short time and generates a very high self-induction voltage at the connection terminals, which can damage the insulation or other circuit parts. To avoid this, inductive components are often short-circuited with a load resistor before being switched off, in which the energy stored in the magnetic field is thermally converted. However, this high voltage can also be used to supply electrical components with high voltage requirements , such as a spark plug .

Other methods of thermal conversion during switching processes are the protective diodes used in DC voltage circuits .

Internal and external inductance

The term external inductance is used for the contribution of the magnetic flux that occurs in the space outside the electrical conductor to the inductance. In the above examples for determining the inductance of various geometrical conductor arrangements, the cross-sections of the electrical conductors were assumed to be negligibly thin. In this case, the determination of the inductance can be limited to the determination of the external inductance or an idealized field shape.

If, on the other hand, the electrical conductor (wire) has a non-negligible spatial expansion, a corresponding cross-sectional area, a magnetic flux density distribution also occurs within the conductor. The inductance derived from this is referred to as the internal inductance. In the simplest case of a uniform current distribution over the cross section of the conductor with length l , the internal inductance can be determined using the following equation:

${\displaystyle L_{i}={\frac {\mu _{0}\mu _{r}l}{8\pi }}}$

What is remarkable about this is that the internal inductance does not depend on the specific geometric dimensions such as the diameter of the cross-sectional area of ​​the conductor. This expression is only valid with a uniform current distribution, i.e. only with direct current, and only when the cross-sectional area of ​​the conductor has no internal limits. If the current distribution is no longer uniform at higher frequencies due to the skin effect , other, more complex expressions result for the frequency-dependent internal inductance. Because of the current displacement in the conductor, the internal inductances are highly frequency-dependent and decrease to practically zero with increasing frequency.

The internal inductance is particularly important when determining the total inductance of electrical cables , as the conductor cross-sections often cannot be neglected even at low frequencies (e.g. mains frequency).

Inductance of a coaxial line

To determine the inductance of a coaxial cable 's length (so-called inductance coating ), the internal inductances of the inner conductor and the outer conductor must be taken into account at low frequencies . However, the main effect is the inductance of the concentric space between the two conductors. The total inductance of a coaxial line of the length results from the sum of the individual partial inductances: ${\displaystyle l}$ ${\displaystyle L_{ii}}$ ${\displaystyle L_{ia}}$ ${\displaystyle L_{a}}$ ${\displaystyle l}$

${\displaystyle \;L=L_{a}+L_{ii}+L_{ia}\,}$.

In the case of direct current, the above expression for the internal inductance can be used for the inner conductor with the diameter : ${\displaystyle d}$

${\displaystyle L_{ii}={\frac {\mu _{0}\mu _{r}l}{8\pi }}\,}$.

The inner inductance of the outer conductor, which is also strongly frequency-dependent, with the thickness and the inner diameter , which is arranged concentrically as a circular ring, results in the direct current case with : ${\displaystyle s}$ ${\displaystyle D}$ ${\displaystyle x=D/(D+2s)}$

${\displaystyle L_{ia}={\frac {\mu _{0}\mu _{r}l}{8\pi (1-x^{2})^{2}}}\cdot (4x^{2}-x^{4}-3-\ln x)\,}$.

The Taylor expansion gives a good approximation formula for small : ${\displaystyle s}$

${\displaystyle L_{ia}={\frac {\mu _{0}\mu _{r}l}{3\pi }}\cdot {\frac {s}{D}}\,}$.

The frequency-independent external inductance in the dielectric is for coaxial conductors:

${\displaystyle L_{a}={\frac {\mu _{0}\mu _{r}l}{2\pi }}\cdot \ln {\frac {D}{d}}\,}$.

At higher frequencies, from 10 kHz upwards, the two terms of the internal inductance can be neglected because of the skin effect. For the determination of the wave impedance of a coaxial cable at typical frequencies, only the summand of the external inductance is essential. ${\displaystyle L_{a}}$

Mutual inductance

The mutual inductance featuring mutual magnetic action of two or more spatially adjacent circuits. It is also known as magnetic coupling. Mutual inductance is the most important technical application in a transformer.

Non-linear inductance

As a material constant, the relative permeability number μ _r depends not only on the respective material, but also on the magnetic flux density for many materials . At high magnetic flux densities, so-called magnetic saturation of the material occurs and, as a result, the relative permeability number μ _{r is} reduced down to 1. This means that the inductance is directly dependent on the magnetic flux density, which in turn is mostly a function of the flow caused by the coil flowing electric current. Thus, the inductance of a coil changes depending on the instantaneous value of the current flowing through the coil.

The consequence of this is that the dynamic inductance can differ from the static inductance in the case of very small modulations around the operating point. In the case of larger modulations beyond the linear operating point approximation, additional harmonics as non-linear distortions can occur with non-linear inductances in AC voltage applications. In the case of calculations with non-linear inductances, the simple methods of (linear) complex alternating current calculations are no longer directly applicable.

The non-linearity of inductors may be desirable, e.g. B. in memory throttles in switching regulators to better adapt them to different load cases, or in the deflection circuits of tube televisions to counteract the non-linear current flow in the deflection coils. Non-linearity is also desirable in the so-called saturation chokes for suppressing interference from thyristor controllers.

Measuring device

Inductance cannot be measured directly. Only their effect can be determined.

By applying a known alternating voltage and measuring the alternating current flowing through the inductive component (or vice versa), the inductance can be determined via the reactance . For this purpose, the amplitude and phase position are determined. This method is used in simple laboratory measuring devices and provides the inductance value, the quality and the value of an equivalent series or parallel resistance.

A resonant circuit is obtained by connecting a known capacitance to the inductance in parallel . If you determine its resonance frequency , you can deduce the inductance. This method can also be carried out without special equipment and is therefore widespread among hobbyists and amateurs. The accuracy is quite high.

A Maxwell measuring bridge is used for high accuracy . This method is very accurate and may a. used in the automated production of coils.

When determining the inductivity of real coils, it must be noted that, depending on the coil design, the capacitive coupling of the windings and layers becomes effective at very high frequencies. The impedance curve rises up to a maximum value and takes on the character of an oscillating circle, only to drop again to even higher frequencies - the coil then represents a capacitance.

Inductance as a disturbing property

Every electrical current creates a magnetic field (electromagnetism) in which magnetic energy is stored. Thus, every piece of electrical conductor has a small inductance. As a rough estimate, an inductance of around 1.2 nH per millimeter of cable length can be calculated on circuit boards . In summary, these inductances result in the parasitic structural inductance of an electrical circuit.

The magnetic fields of conductor pieces that are close together influence each other through the magnetic coupling. Are z. B. The outward and return lines of a circuit are very close together, their magnetic fields partially cancel each other out, which greatly reduces the total inductance of this arrangement. For this reason, current paths are often run close together and cables are twisted together .

If the current is to change in an inductive conductor loop, a voltage U _ind proportional to the current rate of change d i / d t must be effective:

${\displaystyle U_{\mathrm {ind} }=L\cdot {\frac {\mathrm {d} i}{\mathrm {d} t}}\,}$.

Switches and relays that are often used to switch loads with inductive behavior therefore show clear signs of wear on the contacts, which can severely impair their function: when switching off, the current continues to flow due to the inductance and forms an arc (see switching arc ) in which the Energy stored in the inductor discharges. Changes in the current flow caused by semiconductor switches are even more critical. Semiconductor components are often destroyed by such high voltages. Therefore, when designing circuits with high rates of current change, attention must be paid to a low-inductance structure. In addition, snubber networks are often attached to the semiconductor. If possible and necessary, free-wheeling diodes are also used. Newer semiconductor switches can often switch inductive loads without a protective circuit, in that the energy dissipation takes place in a controlled avalanche breakdown.

Another problem with parasitic inductances is the interaction with parasitic capacitances. The resulting resonant circuit can generate disruptive voltage oscillations that can damage semiconductor components and impair electromagnetic compatibility and signal transmission properties.

In computers, the power requirements of individual integrated circuits can change every nanosecond. Because this corresponds to a frequency in the gigahertz range, the inductance of the power supply lines cannot be ignored, even if they are only a few centimeters short. The inductive resistance of the wire increases the internal resistance of the voltage source quite considerably with increasing frequency. As a result, the voltage can fluctuate between 2 V and 10 V when the current changes, for example, and disrupt or even destroy the IC. As an antidote, low-inductance capacitors are placed directly on the IC connections, which ensure a very low dynamic internal resistance.

Computational techniques

In the most general case, current distribution and magnetic field are to be determined from Maxwell's equations. In the case of conductor loops made of thin wires, on the other hand, the current distribution is at least approximately specified, but the skin effect and shielding currents also result in complications and case distinctions here.

Mutual inductivity of two conductor loops

The mutual inductance of two “thread-like” conductor loops m and n can be determined using the Neumann curve integral

${\displaystyle L_{m,n}={\frac {\mu _{0}}{4\pi }}\oint _{C_{m}}\oint _{C_{n}}{\frac {d\mathbf {x} _{m}\cdot d\mathbf {x} _{n}}{|\mathbf {x} _{m}-\mathbf {x} _{n}|}}}$

receive. The symbol μ ₀ denotes the magnetic field constant , C _m and C _n are the curves spanned by the conductor loops. The formula can be used as a good approximation for real wire loops if the radii of curvature of the loops and the distances between the wires are larger than the wire radius.

Self-inductance of a wire loop

The Neumann formula cannot be used to calculate self-inductances, since the two curves coincide and the integrand diverges. It is necessary to take into account the finite wire radius and the current distribution in the wire cross-section. There remains the contribution of the integral over all point pairs with and a correction term, ${\displaystyle m=n}$ ${\displaystyle 1/|\mathbf {x} -\mathbf {x} '|}$ ${\displaystyle a}$ ${\displaystyle |\mathbf {x} -\mathbf {x} '|>a/2}$

${\displaystyle L=\left({\frac {\mu _{0}}{4\pi }}\oint _{C}\oint _{C'}{\frac {d\mathbf {x} \cdot d\mathbf {x} '}{|\mathbf {x} -\mathbf {x} '|}}\right)_{|\mathbf {x} -\mathbf {x} '|>a/2}+{\frac {\mu _{0}}{4\pi }}lY+O\left(\mu _{0}a\right).}$

The symbols and stand for the radius and length of the wire, is a constant that depends on the current distribution: if the current flows in the wire surface ( skin effect ) , if the current density in the wire cross-section is constant. The error is small if the wire loop is large in relation to the wire radius. ${\displaystyle a}$ ${\displaystyle l}$ ${\displaystyle Y}$ ${\displaystyle Y=0}$ ${\displaystyle Y=1/2}$ ${\displaystyle O(\mu _{0}a)}$

Method of mirror currents

In some cases, different current distributions in a room create an identical magnetic field. This fact can be used to relate self-inductances to each other (see also mirror charge ). An example are the two systems:

• A wire at a distance in front of a perfectly conductive wall (the current returns in the wall) ${\displaystyle d/2}$
• Two parallel wires spaced apart , opposite current ${\displaystyle d}$

The magnetic field of the two systems is identical (in a half space). The magnetic field energy and inductance of the second system are therefore twice as large as those of the first.

Relationship between inductance and capacitance

In the case of a conductor pair consisting of two parallel conductors ideal arbitrary constant cross-section is between the inductance per unit length and capacitance per unit length , the relationship ${\displaystyle L'}$ ${\displaystyle C'}$

${\displaystyle \displaystyle L'C'={\varepsilon \mu }.}$

Here ε and µ stand for the dielectric permittivity and the magnetic permeability of the surrounding medium. There is no electric and no magnetic field in the conductors (full skin effect , high frequency). Outside the conductor, the electric and magnetic fields are perpendicular to each other everywhere. Signals propagate along the lines at the same speed as free electromagnetic radiation in the surrounding medium.

Self-inductance of simple circuits

The self-inductances of many types of circuits can be specified exactly or to a good approximation.

Self-inductance of conductor loops

Type	Self inductance	comment
One-layer solenoid	${\displaystyle {\frac {\mu _{0}r^{2}N^{2}}{3l}}\left[-8w+{\frac {2}{w{\sqrt {m}}}}\left(K\left({\sqrt {m}}\right)-{\frac {1-2m}{1-m}}E\left({\sqrt {m}}\right)\right)\right]}$ ${\displaystyle ={\frac {\mu _{0}r^{2}N^{2}\pi }{l}}\left[1-{\frac {8w}{3\pi }}+\sum _{n=1}^{\infty }{\frac {\left(2n\right)!^{2}}{n!^{4}\left(n+1\right)\left(2n-1\right)2^{2n}}}\left(-1\right)^{n+1}w^{2n}\right]}$ ${\displaystyle ={\frac {\mu _{0}r^{2}N^{2}\pi }{l}}\left(1-{\frac {8w}{3\pi }}+{\frac {w^{2}}{2}}-{\frac {w^{4}}{4}}+{\frac {5w^{6}}{16}}-{\frac {35w^{8}}{64}}+\dots \right)}$at w  ≪ 1 at w  ≫ 1 ${\displaystyle =\mu _{0}rN^{2}\left[\left(1+{\frac {1}{32w^{2}}}+O\left({\frac {1}{w^{4}}}\right)\right)\ln(8w)-1/2+{\frac {1}{128w^{2}}}+O\left({\frac {1}{w^{4}}}\right)\right]}$	${\displaystyle N:}$Number of turns Radius Length Elliptical integral Elliptical integral ${\displaystyle r:}$ ${\displaystyle l:}$ ${\displaystyle w=r/l}$ ${\displaystyle m=4w^{2}/(1+4w^{2})}$ ${\displaystyle K:}$ ${\displaystyle E:}$
Coaxial cable, high frequency	${\displaystyle {\frac {\mu _{0}l}{2\pi }}\ln \left({\frac {a_{1}}{a}}\right)}$	${\displaystyle a_{1}:}$Outside radius Inside radius length ${\displaystyle a:}$ ${\displaystyle l:}$
Circular wire loop	${\displaystyle \mu _{0}r\cdot \left(\ln \left({\frac {8r}{a}}\right)-2+Y/2+O\left(a^{2}/r^{2}\right)\right)}$	${\displaystyle r:}$Loop radius wire radius ${\displaystyle a:}$
rectangle	${\displaystyle {\frac {\mu _{0}}{\pi }}\left(b\ln \left({\frac {2b}{a}}\right)+d\ln \left({\frac {2d}{a}}\right)-\left(b+d\right)\left(2-{\frac {Y}{2}}\right)+2{\sqrt {b^{2}+d^{2}}}\right)}$ ${\displaystyle \;\;-{\frac {\mu _{0}}{\pi }}\left(b\cdot \operatorname {arsinh} \left({\frac {b}{d}}\right)+d\cdot \operatorname {arsinh} \left({\frac {d}{b}}\right)+O\left(a\right)\right)}$	${\displaystyle a:}$Wire radius : Edge length : Edge length ${\displaystyle b\gg a}$ ${\displaystyle d\gg a}$
Two parallel wires	${\displaystyle {\frac {\mu _{0}l}{\pi }}\left(\ln \left({\frac {d}{a}}\right)+Y/2\right)}$	${\displaystyle a:}$Wire radius distance, length of wire pair ${\displaystyle d:}$ ${\displaystyle d\geq 2a}$ ${\displaystyle l:}$
Two parallel wires, high frequency	${\displaystyle {\frac {\mu _{0}l}{\pi }}\operatorname {arcosh} \left({\frac {d}{2a}}\right)={\frac {\mu _{0}l}{\pi }}\ln \left({\frac {d}{2a}}+{\sqrt {{\frac {d^{2}}{4a^{2}}}-1}}\right)}$	${\displaystyle a:}$Wire radius distance, length of wire pair ${\displaystyle d:}$ ${\displaystyle d\geq 2a}$ ${\displaystyle l:}$
Wire parallel to perfectly conductive wall	${\displaystyle {\frac {\mu _{0}l}{2\pi }}\left(\ln \left({\frac {2d}{a}}\right)+Y/2\right)}$	${\displaystyle a:}$Wire radius distance, length ${\displaystyle d:}$ ${\displaystyle d\geq a}$ ${\displaystyle l:}$
Wire parallel to conductive wall, high frequency	${\displaystyle {\frac {\mu _{0}l}{2\pi }}\operatorname {arcosh} \left({\frac {d}{a}}\right)={\frac {\mu _{0}l}{2\pi }}\ln \left({\frac {d}{a}}+{\sqrt {{\frac {d^{2}}{a^{2}}}-1}}\right)}$	${\displaystyle a:}$Wire radius distance, length ${\displaystyle d:}$ ${\displaystyle d\geq a}$ ${\displaystyle l:}$

The symbol μ ₀ stands for the magnetic field constant (4π × 10 ⁻⁷ H / m). At high frequencies, the current flows in the surface of the conductor ( skin effect ), and depending on the geometry, one sometimes has to distinguish between high-frequency and low-frequency inductances. The constant is used for this : if the current is evenly distributed over the wire surface (skin effect), if the current is uniformly distributed over the wire cross-section. In the case of the skin effect, it should also be noted that if the distance between the conductors is small, additional shielding currents are induced, and the expressions contained therein then become imprecise. ${\displaystyle Y}$ ${\displaystyle Y=0}$ ${\displaystyle Y=1/2}$ ${\displaystyle Y}$

literature

• Frederick W. Grover: Inductance Calculations: Working Formulas and Tables . Reprint edition. Dover Publications, New York 1952.
• Karl Küpfmüller, Gerhard Kohn: Theoretical electrical engineering and electronics. An introduction . 14th edition. Springer-Verlag, Berlin 1993, ISBN 3-540-56500-0 .
• Otto Zinke , Heinrich Brunswig: High frequency technology I. High frequency filters, lines, antennas . 5th edition. Springer-Verlag, Berlin 1995, ISBN 3-540-58070-0 .
• Howard Johnson: High-Speed ​​Digital Design . Prentice-Hall, New Jersey 1993, ISBN 0-13-395724-1 .

Web links

• Clear explanation of the passive components (including inductance) in the water model

Remarks

1. ↑ ^{a b c} J.D. Jackson: Classical Electrodynamics . Wiley, 1975, p. 262.
2. ↑ ^{a b} E. Rebhan: Theoretical Physics: Electrodynamics . Spectrum Academic Publishing House, Heidelberg, + Elsevier, 2007.
3. ^ Glenn Elert: The Physics Hypertextbook: Inductance. 2018, accessed September 1, 2018 . 
4. ^ Gustav Benischke: The scientific foundations of electrical engineering , Springer-Verlag, Berlin / Heidelberg, 1907, p. 570.
5. ^ FE Neumann: General Laws of Induced Electric Currents . In: Treatises of the Royal Academy of Sciences in Berlin, from 1845 . 1847, pp. 1-87.
6. ^ ^{A b} Richard Dengler: Self inductance of a wire loop as a curve integral . In: Advanced Electromagnetics . 2016. doi : 10.7716 / aem.v5i1.331 .
7. ↑ L. Lorenz: About the propagation of electricity . In: Annals of Physics . VII, 1879, pp. 161-193. (The given expression gives the inductance of a cylinder with a current around its outer surface).
8. ↑ EB Rosa: The Self and Mutual Inductances of Linear Conductors . In: Bulletin of the Bureau of Standards . 4, No. 2, 1908, pp. 301-344.