Solenoid

Solenoid

A cylinder coil is a coil in which the wire winding lies on a cylinder jacket, i.e. is thin compared to the cylinder diameter.

An ideal cylinder coil also has a very small distance between the wire windings in relation to the diameter and thus a very high number of windings. A solenoid for generating a (spatially as constant as possible) magnetic field is sometimes referred to as a solenoid . Types of cylinder coils are described under air-core coil . Cylinder coils are usually single-layer, that is, they have a helical course of the wire.

In the limiting case of a very short length, the solenoid turns into a circular conductor loop .

Technical importance

In addition to being easy to manufacture and calculate, solenoid coils have the following features in technical applications:

• particularly suitable for high frequencies because
  • less capacitive coupling between terminals than multi-layer coils or toroidal coils
  • high natural resonance frequency
• Better suited for high voltages because of the elimination of the problems of layer insulation
• larger dimensions, but better dissipation of heat loss than multi-layer coils with the same inductivity

Cylinder coils can be well balanced by bending or pulling their windings apart or by inserting an aluminum, ferrite or iron powder core. See also variometer . The range of variation that can be achieved is higher than with a short, multi-layer coil.

The Compact Muon Solenoid (CMS) particle detector at CERN is a prominent example of the large-scale application of solenoid coils .

Magnetic field

Magnetic field of a solenoid (in cross section). The wire windings are marked by "×" (current flows into the image plane) and "·" (current flows out of the image plane).

Magnetic field of a solenoid with ten turns. The cutting plane runs axially through the center.

Magnetic field | B | an ideal solenoid. The cutting plane runs axially through the center. The radial field diverges at the end edges .

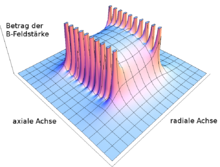
The magnetic field B of an ideal solenoid can be calculated by integrating the Biot-Savart law . The coil had the winding number N , current intensity I , length l and radius R . We denote the cylinder axis by the unit vector , where z is measured from the center of the coil in the direction of the corkscrew rule. The distance to the cylinder axis is ρ with a corresponding unit vector ( cylinder coordinates ). Then the generated field has only one axial and radial, but no azimuthal component: ${\displaystyle {\hat {z}}}$ ${\displaystyle {\hat {\rho }}}$

${\displaystyle {\vec {B}}(\rho \,{\hat {\rho }}+z\,{\hat {z}})=B_{\rho }(\rho ,z)\,{\hat {\rho }}+B_{z}(\rho ,z)\,{\hat {z}}}$

The field components are:

${\displaystyle B_{\rho }={\frac {\mu _{0}}{4\pi }}{\frac {NI}{l}}{\frac {1}{\rho }}\left[{\sqrt {(\rho +R)^{2}+\zeta ^{2}}}{\Bigl (}(2-m)\,K(m)-2\,E(m){\Bigr )}\right]_{\zeta =z+l/2}^{\zeta =z-l/2}}$

${\displaystyle B_{z}={\frac {\mu _{0}}{2\pi }}{\frac {NI}{l}}\left[{\frac {\zeta }{\sqrt {(\rho +R)^{2}+\zeta ^{2}}}}\left({\frac {\rho -R}{\rho +R}}\,\Pi (n,m)-K(m)\right)\right]_{\zeta =z+l/2}^{\zeta =z-l/2}}$

The content of the square brackets is subtracted according to . Here the magnetic field constant μ ₀ , the substitutions ${\displaystyle [f(x)]_{x=a}^{x=b}=f(b)-f(a)}$

${\displaystyle m=4R\rho /\left((\rho +R)^{2}+\zeta ^{2}\right)}$,     ${\displaystyle n=4R\rho /(\rho +R)^{2}}$

as well as the complete elliptic integrals of the first ( K ), second ( E ) and third kind ( Π ):

${\displaystyle K(m)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-m\sin ^{2}\varphi }}}\,\mathrm {d} \varphi }$

${\displaystyle E(m)=\int _{0}^{\pi /2}{\sqrt {1-m\sin ^{2}\varphi }}\,\mathrm {d} \varphi }$

${\displaystyle \Pi (n,m)=\int _{0}^{\pi /2}{\frac {1}{(1-n\sin ^{2}\varphi ){\sqrt {1-m\sin ^{2}\varphi }}}}\,\mathrm {d} \varphi }$

In addition to the representation using the classic elliptical integrals, there are also alternative expressions with improved numerical stability and more efficient computability, for example with Carlson forms .

The field is simplified along the cylinder axis:

${\displaystyle {\vec {B}}(z\,{\hat {z}})={\hat {z}}\,\mu _{0}{\frac {NI}{2l}}\left({\frac {z+l/2}{\sqrt {R^{2}+(z+l/2)^{2}}}}-{\frac {z-l/2}{\sqrt {R^{2}+(z-l/2)^{2}}}}\right)}$

In the center of the coil the field is exactly:

${\displaystyle {\vec {B}}(0)={\hat {z}}\,\mu _{0}{\frac {NI}{\sqrt {(2R)^{2}+l^{2}}}}}$

For long coils the field is anywhere inside except near the ends ${\displaystyle l\gg 2R}$

${\displaystyle {\vec {B}}\approx {\hat {z}}\,\mu _{0}{\frac {NI}{l}}}$

and quickly drops to zero and outside far away from the coil ends. For large distances the field approaches a dipole field with a magnetic moment : ${\displaystyle \rho ^{2}+z^{2}\gg R^{2}+(l/2)^{2}}$ ${\displaystyle {\vec {m}}=NIR^{2}\pi \,{\hat {z}}}$

${\displaystyle {\vec {B}}(\rho \,{\hat {\rho }}+z\,{\hat {z}})\approx {\frac {\mu _{0}}{4}}NIR^{2}{\frac {3\rho z\,{\hat {\rho }}+(2z^{2}-\rho ^{2}){\hat {z}}}{{\sqrt {\rho ^{2}+z^{2}}}^{5}}}}$

The magnetic field of the solenoid corresponds exactly to that of a homogeneously magnetized cylindrical bar magnet with magnetization , where . ${\displaystyle M}$ ${\displaystyle NI\;{\widehat {=}}\;Ml}$

Inductance

The inductance of a solenoid in a vacuum is

${\displaystyle L={\frac {8\mu _{0}N^{2}R^{2}}{3\,l}}\left({\frac {1}{2k}}\operatorname {cel} \left(k,1,1,2k^{2}\right)-{\frac {R}{l}}\right),\quad k={\frac {l/2}{\sqrt {R^{2}+(l/2)^{2}}}}}$.

Here cel is the elliptical Bulirsch integral and is the magnetic field constant . For specific aspect ratios this is: ${\displaystyle \mu _{0}}$

${\displaystyle l/R}$	0.01	0.1	0.5	1	2	5	10	100	∞
${\displaystyle L{\bigg /}{\frac {\mu _{0}N^{2}R^{2}\pi }{l}}}$	0.0197	0.124	0.365	0.526	0.688	0.850	0.920	0.9916	1

A simple approximation formula for not too short coils is

${\displaystyle L\approx {\frac {\mu _{0}N^{2}R^{2}\pi }{l+0{,}9\cdot R}}}$.

This formula has errors for less than 1%. ${\displaystyle l>0{,}8R}$

In the case of a very long solenoid ( ) with a cross-sectional area , the approximation can be simplified even further: ${\displaystyle l\gg R}$ ${\displaystyle A=R^{2}\pi }$

${\displaystyle L\approx {\frac {\mu _{0}N^{2}A}{l}}}$.

The formula can no longer be used for coils with a ferromagnetic core , as the outer part of the field is now relevant. If, however, it is a closed magnetic circuit in the form of a highly permeable frame on which the coil is wound, its mean circumference - that is the mean magnetic path length - and instead of the coil cross-section its mean cross-section can be used instead of the coil length. The inductance calculation then requires the multiplication by the permeability number of the core material. ${\displaystyle \mu _{r}}$

Individual evidence

1. ^ JC Maxwell: Electricity and Magnetism . Clarendon Press, Oxford, England 1873 ( archive.org ).
2. ↑ Karl Friedrich Müller: Calculation of the inductance of coils . In: Archives for electrical engineering . 17, No. 3, May 1, 1926, pp. 336-353. ISSN  1432-0487 . doi : 10.1007 / BF01655986 .
3. ↑ Kuno Foelsch: Magnetic field and inductance of a cylindrical coil . In: Archives for electrical engineering . 30, No. 3, March 3, 1936, pp. 139-157. ISSN  1432-0487 . doi : 10.1007 / BF01657310 .
4. ^ EE Callaghan, SH Maslen: The Magnetic Field of a Finite Solenoid . In: NASA Technical Reports . NASA-TN-D-465, E-900, October 1, 1960 ( nasa.gov ).
5. ^ MW Garrett: Calculation of Fields, Forces, and Mutual Inductances of Current Systems by Elliptic Integrals . In: Journal of Applied Physics . 34, No. 9, September 1963, pp. 2567-2573. doi : 10.1063 / 1.1729771 .
6. ↑ Derivation: Finite length Solenoid potential and field ( Memento from March 7, 2017 in the Internet Archive ) (contains errors)
7. ^ ^{A b c d} Norman Derby, Stanislaw Olbert: Cylindrical magnets and ideal solenoids . In: American Journal of Physics . 78, No. 3, 2010, ISSN  0002-9505 , pp. 229-235. arxiv : 0909.3880 . doi : 10.1119 / 1.3256157 .
8. ^ HA Wheeler: Simple Inductance Formulas for Radio Coils . In: Proceedings of the Institute of Radio Engineers . tape 16 , no. 10 , 1928, pp. 1398-1400 , doi : 10.1109 / JRPROC.1928.221309 .