Ferromagnetism

Ferromagnetism causes the lower piece of iron to be attracted to a horseshoe magnet .

Schematic course of the magnetic induction B from ferromagnetic ( ), paramagnetic ( ) and diamagnetic materials ( ) to vacuum ( )

{\ displaystyle \ mu _ {\ mathrm {f}}}

{\ displaystyle \ mu _ {\ mathrm {p}}}

{\ displaystyle \ mu _ {\ mathrm {d}}}

{\ displaystyle \ mu _ {0}}

Ferromagnetism (from Latin ferrum 'iron' ) is the best known type of magnetism in solids . It is explained by the fact that the magnetic moments ( elementary magnet ) of the atoms of the material tend to align themselves in parallel. Ferromagnets either generate a permanent magnetic field themselves or are strongly attracted by a pole of an external magnetic field. Ferromagnetic materials are usually solids. Known applications include a. Permanent magnets , electric motors , transformers and the various forms of magnetic data storage ( magnetic tape , floppy disk , hard disk drive ).

As pure metals, iron , cobalt and nickel are ferromagnetic at room temperature (approx. 20 ° C). At lower temperatures, some lanthanoids are also ferromagnetic, e.g. B. Gadolinium at up to 19.3 ° C.

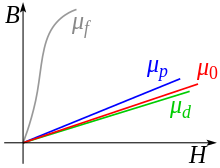
Ferromagnetic materials are magnetized in an external magnetic field in such a way that the magnetic flux density increases in their interior compared to the exterior, and are thereby drawn in the direction of higher field strengths ("into the magnetic field"). The factor of the increase in flux density compared to the empty space is described by the magnetic permeability (or the magnetic susceptibility ) of the material; applies to ferromagnets . Other types of stable magnetic order of elementary magnets are antiferromagnetism and ferrimagnetism . ${\ displaystyle \ mu _ {\ mathrm {r}}}$ ${\ displaystyle \ mu _ {\ mathrm {r}} -1}$ ${\ displaystyle \ mu _ {\ mathrm {r}} \ gg 1}$

An increase in the flux density in the material also occurs with paramagnetic substances. With them, however, there is no stable long-range order of the magnetic moments. Therefore the effect is usually weaker.

Ferromagnets show the tendency to maintain their magnetic order even against external influences. That leads u. a. to the fact that they maintain the internal magnetic order and thus the external magnetic field generated by them, even if they are no longer exposed to a magnetic field. This tendency is known as the remanence of ferromagnetism. It is caused by effects of two different magnitudes:

microscopic : the rectified magnetic order of the elementary magnets (e.g. the electron spins, see below ) on an atomic scale

macroscopic : the arrangement of the Weiss areas (so-called "domains") in the order of magnitude from micrometers to nanometers

Many considerations in theoretical solid-state physics are limited to the microscopic aspect and already refer to the rectification of elementary magnets as ferromagnetism. On the other hand, the Weiss domains also occur in other magnetic orders.

introduction

Typical hysteresis curve of ferromagnetic systems :
The new curve (first magnetization!) Is in blue, the gradients with repeated changing magnetization are shown in green.
The remanence magnetization and the coercive field strength (the axis values!) Are marked.

A material is classified or declared as a ferromagnetic substance if the magnetic moments of the atoms align themselves in parallel below the Curie temperature . This effect is due to the fact that there is an interaction between the atoms in these materials, which means that the total energy of the material is reduced by the order compared to a disordered configuration.

This tendency of the elementary magnets to align themselves in parallel leads to a spontaneous magnetization of larger areas, the Weiss areas , in which the elementary magnets are largely aligned in parallel. This distinguishes ferromagnets from paramagnets, in which the magnetic moments are usually disordered.

Without external influences, the directions of the magnetic fields of neighboring Weisser areas are anti-correlated. In the Bloch and Neel walls between the districts, the elementary magnets are aligned so that there is a transition between the two directions of magnetization. In this state, a body made of a ferromagnetic material does not generate an external magnetic field, as the fields of the different Weiss areas compensate each other.

If the material is exposed to an external magnetic field , the Weiss areas, which are magnetized in the opposite direction to the external magnetic field, shrink and finally fold over. This creates a macroscopic magnetization, the field of which is superimposed on the external one in such a way that the field lines appear to be drawn laterally into the material. In an inhomogeneous field, the material magnetized in this way is drawn to locations of greater field strength, be it magnetic north or south poles. Paramagnets behave similarly, but the alignment of the magnetic moments takes place exclusively due to the external field and not additionally due to the parallelizing influence of the neighboring moments. Therefore the effect is much weaker.

Ferromagnetic materials are classified according to the behavior they show when they are removed from a magnetic field. In general, a residual magnetism then remains, the so-called remanence .

In soft magnetic materials , the remanence is low; that is, most of the magnetization is lost immediately when the object is removed from the external magnetic field, especially after alternating fields have been applied.
Hard magnetic materials are more difficult to magnetize, but retain a greater permanent magnetization. Such materials, e.g. B. hardened steel, can be magnetized to permanent magnets or exist from the outset as permanent magnets, that is, assume a clearly recognizable (macroscopic) magnetization permanently.

The remanence magnetization can be eliminated by applying an opposing magnetic field, which happens when the coercive field strength is reached. In the case of hard magnetic substances, the height of the required opposing field is greater than in the case of soft magnetic substances. In the case of permanent magnets, both a high remanence and a high coercive field strength are desirable.

Ferromagnetism is to be distinguished from ferrimagnetism (e.g. in ferrites ), which macroscopically has similar properties, but microscopically related to antiferromagnetism . As in antiferromagnetism, the elementary magnets are alternately directed in opposite directions, but differently pronounced in the two directions, which is why - unlike in antiferromagnetism - one magnetization remains for each pair.

Substances with ferromagnetic properties

substance	${\ displaystyle T _ {\ mathrm {C}}}$ in K
Co	1395
Fe	1033
Ni	627
CrO ₂	390
Gd	289
Tb	219
Dy	85
EuO	70
Ho	20th
He	19th

Among the elements or metals in pure form, iron , nickel and cobalt have ferromagnetic properties at room temperature . In 2018, ruthenium was identified as the fourth element with ferromagnetic properties at room temperature (in the metastable body-centered tetragonal phase). At lower temperatures (see table) the lanthanoids gadolinium , terbium , dysprosium , holmium and erbium also become ferromagnetic.

In practice, ferromagnetic alloys such as B. AlNiCo , SmCo , Nd ₂ Fe ₁₄ B , Ni ₈₀ Fe ₂₀ (“ Permalloy ”), or NiFeCo alloys (“ Mumetall ”). It is noteworthy that under certain circumstances some compounds of generally non-ferromagnetic elements also exhibit ferromagnetic behavior, for example chromium dioxide , manganese arsenide , europium (II) oxide or the superfluid A-1 phase of He-3 , as well as the so-called Heusler alloys .

It is also noteworthy that the best-known ferromagnetic material, iron, as the main component of an austenitic alloy, does not have a ferromagnetic effect. Austenitic structures are a component of many stainless steels and some types of stainless steel . (Iron crystallizes in a body-centered cubic lattice at room temperature . Austenitic alloys, on the other hand, are predominantly face-centered .)

In general, the presence of ferromagnetic properties depends on the fact that unpaired electrons are present in the electron configuration of the ground state of the metal or compound in question, which essentially only occurs with transition metals and rare earths.

Ferromagnetism normally only occurs in the solid state because the Curie temperature of these materials is lower than the melting temperature. Ferromagnetism was also observed in a supercooled melt. Ferrofluids are suspensions of solid magnetic particles in a non-magnetic liquid.

Physical origin

Three examples of a ferromagnetic order of a linear chain of magnetic moments

The electron spins are the carriers of the elementary magnetic moments . As with other cooperative magnetic phenomena, in ferromagnetism the magnetic dipole-dipole interaction is far too weak to be responsible for the order of the spins. However, in contrast to the exchange interaction (see below), it has a very large range and is therefore still important for the applications. In the case of the ferromagnetic order, the parallel alignment of magnetic moments is energetically unfavorable for the dipole-dipole interaction. The quantum mechanical exchange interaction is responsible for the parallel spin order of the ferromagnet, which has to do with the existence of singlet and triplet states in two-electron systems and is related to the Pauli principle . So it is a non-classical phenomenon that is not easy to understand:

In detail, according to the Pauli principle, for an antisymmetrical spatial wave function the associated spin wave function must be symmetrical (e.g. for parallel spins in a two-electron system). It can be shown that the average distance between the two particles is greater for an antisymmetric spatial wave function and thus their Coulomb repulsion is lower for particles with the same charge. The exchange interaction brings about an effective lowering of the potential energy. On the other hand, according to the Pauli principle, the electrons with parallel spin cannot be in the same spatial state and must gradually occupy higher levels, which increases their kinetic energy. The spontaneous parallel position of the spins and thus a ferromagnetic order will only come about if the decrease in potential energy overcompensates for the increase in kinetic energy. That is the reason why only the few materials mentioned are ferromagnetic, but the vast majority are not.

The Bethe-Slater curve , which shows the exchange interaction as a function of the relative atomic distance, is a clear illustration of this . B. for common metals ( Cr , Mn , Fe , Co , Ni ). The relative atomic distance is the ratio of the atomic distance of the neighboring atoms to the diameter of the not closed electron shell.

In one sentence:

The order of the magnetic moments is mediated by the (quantum mechanical) exchange interaction , not by (classical) magnetic interaction .

The magnetic conductivity and thus the magnetic susceptibility is not constant in ferromagnets, but a complicated function of the applied field strength and depends on the magnetization history. Therefore, the (differential) magnetic susceptibility is usually regarded as the derivation of the magnetization according to the field strength. It disappears in the saturation area. ${\ displaystyle \ mu = \ mu _ {0} (1+ \ chi)}$ ${\ displaystyle \ chi}$ ${\ displaystyle \ chi}$

The relationship also applies to the relationship between magnetization and magnetic flux density ${\ displaystyle {\ vec {M}}}$ ${\ displaystyle {\ vec {B}}}$

{\ displaystyle {\ vec {B}} = \ mu {\ vec {H}} = \ mu _ {0} ({\ vec {H}} + \ chi {\ vec {H}}) = \ mu _ {0} ({\ vec {H}} + {\ vec {M}}).}

Weiss districts, domains and domain walls

Magneto-optical recording of the magnetic phases, grain geometries and domain orientations in non-grain-oriented transformer sheet (recording using a magneto-optical sensor and polarization microscope)

Electromagnetic dynamic domain investigation of transformer sheet metal (grain-oriented)

Ferromagnetism arises from the fact that elementary magnetic moments have a parallel order which, due to the mutual interaction of the moments, persists even without an external magnetic field. The areas of equal magnetization are called domains or Weiss areas . They occur in sizes from 0.01 µm to 1 µm and are not uniformly oriented in the non-magnetized state of the substance.

The exchange interaction only works between fermions whose wave functions have a substantial overlap, i.e. usually only between nearby particles. The magnetic interaction, on the other hand, also works between distant magnetic moments. Therefore, in an extended ferromagnet, the magnetic energy expenditure at some point exceeds the energy gain of the exchange interaction. The ferromagnetic order of the solid then breaks down into differently oriented domains. The areas of the solid in which domains with different orientations meet are called the domain wall. Depending on the rotation of the magnetization in the wall, one speaks of Bloch walls or Néel walls (with Bloch walls, the magnetization is rotated perpendicular to the wall plane; with Néel walls, on the other hand, it takes place within the wall plane; Néel walls only dominate with very thin magnetic layers). There are also other wall types with topological singularities, so-called Bloch lines and Bloch points, which are associated with changes in the rotational behavior within the wall. These differences, which can be in the 10 nanometer range, are subtle but interesting for current applications in information technology.

The formation of the domain wall requires work to be done against the exchange interaction ; the downsizing of domains (the volume of a contiguous domain) reduces the magnetic energy of a solid.

Due to the non-continuous alignment of the Weiss districts under the influence of external magnetic fields, so-called Barkhausen jumps can be observed.

The magnetic order is broken at high temperatures, the ferromagnets are then only paramagnetic . The temperature above which the ferromagnetic order disappears is called the Curie temperature (after Pierre Curie , the husband of Marie Curie ). The susceptibility can be calculated above the Curie temperature using the Curie-Weiss law . Paramagnetism is retained for all temperatures above the Curie temperature, even after the solid has passed into the liquid or gas phase. ${\ displaystyle T _ {\ mathrm {C}}}$

saturation

Magnetization curves of nine ferromagnetic substances down to the saturation range. 1. Sheet steel , 2. Silicon steel , 3. Cast steel , 4. Tungsten steel , 5. Magnetic steel , 6. Cast iron , 7. Nickel , 8. Cobalt , 9. Magnetite

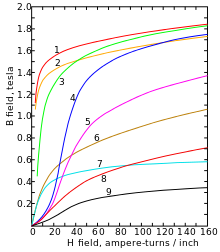
material	Flux density in Tesla at the onset of saturation
Steel "1.3505"	0.5
Steel "C15"	0.45
Cobalt - iron (Fe with 47 to 50% Co)	2.35
Silicon - iron (Fe with 3 to 4% Si)	1.5 to 2
Nickel- iron (Fe with 30 to 50% Ni)	1.2 to 1.5
Ferrite (MnZn)	0.4
Ferrite (NiZn)	0.2

In the case of ferromagnetic substances, saturation magnetization often appears, a material-specific maximum value of magnetization that cannot be exceeded even by increasing the external magnetic field strength . The derivation of the magnetization according to the field strength, the differential magnetic susceptibility ${\ displaystyle M}$ ${\ displaystyle H}$

{\ displaystyle \ chi = {\ frac {\ partial M} {\ partial H}}}

,

disappears in the saturation area.

Particularly good conductivity for the magnetic flux is the main property of ferromagnetic materials such as soft iron , dynamo sheet or certain ferrites . This is why these materials are used where the spatial guidance of magnetic fluxes is important, such as in electromagnets and in the iron cores of transformers. In the area of saturation, the magnetic conductivity decreases sharply. Therefore, saturation is usually undesirable in these technical applications. ${\ displaystyle \ Phi}$

If the magnetic flux density for a material is plotted against the externally applied magnetic field strength in a diagram, the hysteresis curve (magnetization curve) results . The flattening of the slope clearly marks the beginning of the saturation magnetization, one can also speak of reaching the saturation flux density or the saturation induction . ${\ displaystyle B}$ ${\ displaystyle H}$

Saturation in practice

In geophysics , materials are identified by determining their specific Curie temperature by determining the dependence of the saturation magnetization on the temperature.
In transformers and electric motors , magnetic saturation of the core is undesirable because it reduces the efficiency and the transmitted power. (The exception is the reluctance motor , which uses saturation to increase the power factor). To avoid saturation, magnetic cores in transformers and electric motors must have a corresponding minimum cross-sectional area.
In magnetic voltage regulators , the saturation of a transformer core is used to stabilize brief fluctuations in unstable power grids.
By inserting an air gap (perpendicular to the magnetic flux) in a closed coil core, the saturation of ferromagnetic core materials can be prevented or greatly reduced. However, the effective inductance decreases compared to the gapless coil core. This is used, for example, with throttles . Conventional Vorschaltdrosseln of gas discharge lamps and all kinds of storage chokes (also powder cores ) have one or more discrete or so-called (between the powder grains) distributed air gaps.

Hysteresis

Soft hysteresis curve of an EI transformer iron core with an air gap and a relatively large coercive field strength

Hard hysteresis curve of a transformer iron core without an air gap (toroidal core) with a small coercive field strength

In a physical system, hysteresis means that its variable output variable does not depend solely on the input variable, but also on its history. Such a hysteresis behavior occurs with ferromagnetic, magnetically conductive materials such as iron, cobalt, nickel and their alloys. If you increase the magnetic field strength in a previously non-magnetized ferromagnetic material, the magnetic flux density increases in its vicinity . If the field strength is reduced to 0 again, the magnetic flux density remains at a value not equal to 0. The ferromagnetic material retains some residual magnetism (remanence). The magnetic flux density depends not only on the magnetic field strength, but also on its course over time. ${\ displaystyle H}$ ${\ displaystyle B}$

The magnetic flux density in a ferromagnetic material is determined by the strength of the surrounding magnetic field ( ). If it is increased enough, it only increases slightly because of the saturation . If the external magnetic field decreases, the flux density decreases again. The magnetic flux density reaches a higher value at the same value of a field strength which is on the point of decreasing than it occurred during the increase of the field strength. If it is completely reduced to 0, it does not go back to 0, but only to what is known as remanence . In order to bring the magnetization back to 0, an opposing magnetic field with the coercive field strength must be built up. Since there is still an external magnetic field, one does not speak of demagnetization , for which several steps are necessary. If the field strength is reversed again, the lower branch of the hysteresis curve is passed through. This hysteresis process can be illustrated by the course of the hysteresis curve or hysteresis loop . A complete run through of the hysteresis curve is referred to as a hysteresis cycle . The hysteresis curve is point-symmetrical to the origin. The upper branch from the reversal point of the magnetization through the remanence as the -axis section to the coercive field strength on the -axis is called the demagnetization curve. However, only an alternating magnetic field with a decaying amplitude leads to complete demagnetization without an external magnetic field due to the gradual approach of the hysteresis cycles to the zero point. ${\ displaystyle B}$ ${\ displaystyle H}$ ${\ displaystyle H}$ ${\ displaystyle B}$ ${\ displaystyle B}$ ${\ displaystyle H}$ ${\ displaystyle B}$ ${\ displaystyle B_ {R}}$ ${\ displaystyle -H _ {\ mathrm {C}}}$ ${\ displaystyle H}$ ${\ displaystyle y}$ ${\ displaystyle x}$

The cause of the behavior are the so-called Weiss districts . They are characterized by the fact that the spins of the electrons, which can be interpreted as elementary magnets, are parallel to each other within a region. The boundaries between the districts are called Bloch walls . If an external magnetic field is now applied, the areas whose orientation corresponds to the orientation of the magnetic field grow at the expense of the other areas, as electrons in the other areas "flip over", i.e. align themselves parallel to the magnetic field. This clearly corresponds to a shift in the Bloch walls.

However, imperfections that exist in every ferromagnetic (in iron e.g. carbon inclusions) prevent the Bloch walls from shifting evenly. If a Bloch wall encounters an impurity while it is being moved, it first sticks to it, and a kind of bubble forms behind the impurity in which the spins of the electrons do not yet flip. Only after a certain field strength does this bubble close, which leads to a sudden change in magnetization. This process is called the Barkhausen jump . These uneven wall displacements make demagnetization along the new curve impossible. They are the reason for the formation of the hysteresis curve.
When all electron spins in the ferromagnetic are aligned with the field, saturation is reached. If the external field is now removed, not all electrons return to their original orientation. The magnetization drops to the remanence level. Only by supplying additional energy can the material be demagnetized again. Substances with high remanence are not necessarily hard magnetic. Hard magnetic materials ( permanent magnets ) require a high coercive field strength. The remanence in a transformer core is less dependent on the core material, but depends heavily on the shape of the core: A toroidal transformer core has a very high remanence because there are no air gaps in the magnetic circuit. A transformer with technologically conditioned or intentionally built-in air gaps , on the other hand, has a low remanence due to the shear (inclination) of the hysteresis curve, although the core material itself can have a high remanence.

The occurrence of bistable behavior is typical of the hysteresis . If the ambient conditions are the same, the state depends on the past, the voltage time area that was active before switching off. A certain point in the state diagram is reached accordingly .

Taking into account the shape of the hysteresis loop, a substance can be specifically magnetized. Corresponding processes are used in the manufacture of permanent magnets or when writing to magnetic storage media ( magnetic tape , hard disk , core storage ).

Hysteresis losses

When materials are remagnetized, energy has to be used to change the alignment of the Weiss areas. This turning causes heat to develop in the material. The losses are generally proportional to the area within the hysteresis curve and the frequency with which the magnetization is reversed. It should be noted that the hysteresis curve changes with increasing frequency compared to the statically measured curve, since further loss components are added and the relative permeability number decreases.

The area enclosed by the hysteresis curve corresponds to the energy that is converted into heat in the material when it is completely reversed. In electromagnetic components, it becomes noticeable as one of the core loss components or as an additional expenditure of energy. This integral should be as high as possible in the case of storage media. In the case of transformer cores, it should be as small as possible in order to cause only low energy losses.

Magnetically hard and soft materials

In the case of high coercive field strengths one speaks of magnetically hard material, since high field strengths are required for their reorientation. In the case of storage media, this corresponds to a high level of data security, since the written information is not reoriented by random stray fields. In the case of low coercive field strengths, on the other hand, one speaks of magnetically soft material. The designation comes from the fact that pure (i.e. soft) iron is more magnetically soft than magnetic steels. The above-mentioned permalloy , Ni ₈₀ Fe _20, is very soft magnetic . By adding 5% molybdenum , the extremely soft magnetic supermalloy is obtained , with which rooms are shielded in such a way that the extremely weak magnetic fields of brain waves can be measured. The so-called metallic glasses based on iron or cobalt, amorphous alloys, which are similar in structure to liquid metal alloys close to the melting point, are also very soft magnetic .

Practical references of the hysteresis

The course and shape of a hysteresis curve is influenced not only by the basic material properties but also by a possibly existing texture (grain orientation compared to the course of the field lines) or an air gap .

A magnetically soft material can become hard magnetic or even permanent magnetic through plastic deformation (machining process). Glow provides a remedy .

In the earlier common core memories of computers, toroidal cores, which frequently changed their state, became warm and reacted differently to the current impulses than those that were seldom addressed. The remedy was either forced air cooling so that all cores had the same temperature as possible, or a regime for more even use of the cores.

In many applications, small hysteresis cycles are run around points in the - area ; see also small signal behavior . Because of the magnetization-dependent permeability , the effective permeability can vary. ${\ displaystyle B}$ ${\ displaystyle H}$

the hysteresis is fundamental for recording on tape , for example , but causes distortion in audio recordings (see premagnetization ).

The hysteresis behavior of the core material is also important for the design and calculation of transformers with regard to losses.

If materials are remagnetized, energy has to be used to change the alignment of the Weiss areas. This turning causes heat in the iron (hysteresis losses); For example, with induction hobs, 1/3 of the heating power in ferromagnetic pots is provided by hysteresis.

Applications

Ferromagnetic materials have high permeability with on. As a result, the magnetic field lines are conducted well in comparison to the surrounding material (such as air ). That is why ferromagnetic materials are used for the cores of electromagnets and transformers . ${\ displaystyle \ mu _ {\ mathrm {r}} \ gg 1}$ ${\ displaystyle \ mu _ {\ mathrm {r}} \ approx 1}$

Due to the high permeability, coils and chokes for filters or for current limitation can be made smaller.

Further applications are storage media that use the GMR effect and the magnetic tunnel resistance (TMR) (read / write heads on magnetic hard drives ). For this, the 2007 Nobel Prize in Physics was awarded ( Peter Grünberg and Albert Fert ).

literature

Horst Stöcker: Pocket book of physics. 4th edition. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4 .
Hans Fischer: Materials in electrical engineering. 2nd Edition. Carl Hanser Verlag, Munich / Vienna 1982, ISBN 3-446-13553-7 .
Günter Springer: Expertise in electrical engineering. 18th edition. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 .
Richard P. Feynman , Robert B. Leighton, Matthew Sands: Lectures on Physics, Volume 2. 3rd Edition. Oldenbourg Verlag, Munich / Vienna 2001, ISBN 3-486-25589-4 .
Charles Kittel : Introduction to Solid State Physics. 1st edition 1953 to 14th edition 2005, ISBN 0-471-41526-X (German: Introduction to Solid State Physics. Oldenbourg, ISBN 3-486-57723-9 ), see especially the chapter on magnetism.

References and footnotes

↑ P. Quarterman J.-P. Wang et al. a., Demonstration of Ru as the 4th ferromagnetic element at room temperature , Nature Communications, Volume 9, 2018, Article No. 2058

↑ D. Platzek, C. Notthoff et al: Liquid metal undercooled below its Curie temperature . In: Applied Physics Letters . 65, 1994, p. 1723. doi : 10.1063 / 1.112898 .

↑ The impossibility of a classical explanation of ferromagnetism was proven (independently of each other!) As early as 1911 and 1921 by Niels Bohr and Hendryka Johanna van Leeuwen in their respective dissertations, published in:
Niels Bohr: Studier over Metallernes Elektrontheori. Københavns Universitet, 1911.
Hendrika Johanna van Leeuwen: Problems of the théorie électronique du magnétisme. In: Journal de Physique et le Radium. 1921, volume. 2, No. 12, p. 361.
See also the article Bohr-van-Leeuwen theorem . A first quantum mechanical explanation of the phenomenon, the so-called Heisenberg model , was only given in 1928 by Werner Heisenberg .

↑ Strictly speaking, with a strong magnetic field there is still a barely observable, very weak increase in magnetization, the so-called "magnetic para-effect" , see: H. Kronmüller, S. Parkin (Ed.): Handbook of Magnetism and Advanced Magnetic Materials. Wiley, 2007, ISBN 978-0-470-02217-7 . ${\ displaystyle \ Delta M \ propto {\ sqrt {\, H}}}$

↑ Growth, microstructure and hard magnetic properties of Nd-Fe-B layers. P. 13, Google Books.

^ Karl Schüler, Kurt Brinkmann: Permanent magnets: materials and applications . Springer, Berlin 1970.

↑ Lothar Michalowsky, Jürgen Schneider (Ed.): Magnettechnik . Vulkan, Essen 2006, ISBN 978-3-8027-2139-7 .

↑ Instead, the so-called Néel walls appear in very thin layers , see below.

[1] P. Quarterman J.-P. Wang et al. a., Demonstration of Ru as the 4th ferromagnetic element at room temperature , Nature Communications, Volume 9, 2018, Article No. 2058

[2] D. Platzek, C. Notthoff et al: Liquid metal undercooled below its Curie temperature . In: Applied Physics Letters . 65, 1994, p. 1723. doi : 10.1063 / 1.112898 .

[3] The impossibility of a classical explanation of ferromagnetism was proven (independently of each other!) As early as 1911 and 1921 by Niels Bohr and Hendryka Johanna van Leeuwen in their respective dissertations, published in:
Niels Bohr: Studier over Metallernes Elektrontheori. Københavns Universitet, 1911.
Hendrika Johanna van Leeuwen: Problems of the théorie électronique du magnétisme. In: Journal de Physique et le Radium. 1921, volume. 2, No. 12, p. 361.
See also the article Bohr-van-Leeuwen theorem . A first quantum mechanical explanation of the phenomenon, the so-called Heisenberg model , was only given in 1928 by Werner Heisenberg .