Magnetic permeability

Physical size
Surname	magnetic permeability
Formula symbol	${\displaystyle \mu }$
Size and unit system unit dimension SI H  ·  m -1 =  V  ·  s  ·  A -1 ·  m -1 L  ·  M  ·  T −2  ·  I −2 Gauss ( cgs ) c −2 L −2 · T 2 esE ( cgs ) c −2 L −2 · T 2 emE ( cgs ) - 1
See also: Magnetic field constant

Simplified comparison of the permeabilities of ferromagnetic ( ), paramagnetic ( ) and diamagnetic ( ) materials with the vacuum permeability ( ). The slope of the straight line or curve ( #Differential permeability ) is in each case . ${\displaystyle \mu _{f}}$ ${\displaystyle \mu _{p}}$ ${\displaystyle \mu _{d}}$ ${\displaystyle \mu _{0}}$ ${\displaystyle \mu }$ ${\displaystyle B(H)}$

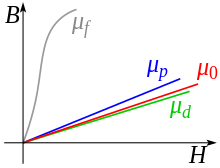
The magnetic permeability (also magnetic conductivity ) determines the ability of materials to adapt to a magnetic field, or more precisely, the magnetization of a material in an external magnetic field. It therefore determines the permeability ( Latin permeare "to go through, penetrate") of matter for magnetic fields . ${\displaystyle \mu }$

A closely related quantity is the magnetic susceptibility .

Basics

The permeability is the ratio of the magnetic flux density to the magnetic field strength : ${\displaystyle \mu }$ ${\displaystyle B}$ ${\displaystyle H}$

${\displaystyle \mu ={\frac {B}{H}}\,.}$

The magnetic field constant is a physical constant and indicates the magnetic permeability of the vacuum. A permeability is also assigned to the vacuum , since magnetic fields can also arise there or electromagnetic fields can propagate. The permeability number , formerly also referred to as relative permeability , is the ratio ${\displaystyle \mu _{0}}$ ${\displaystyle \mu _{\mathrm {r} }}$

${\displaystyle \mu _{\mathrm {r} }={\frac {\mu }{\mu _{0}}}\,.}$

This results in a permeability number of one for the vacuum. The size of the dimension number is related to the magnetic susceptibility via the relationship ${\displaystyle \mu _{\mathrm {r} }}$ ${\displaystyle \chi }$

${\displaystyle \mu _{\mathrm {r} }=1+\chi \,.}$

Complex permeability, permeability number

In electrical engineering in particular, phasors for the fields and a correspondingly complex permeability are used to record time-dependent effects .

${\displaystyle {\hat {\mu }}={\mu _{\mathrm {s} }}'-\mathrm {j} \cdot {\mu _{\mathrm {s} }}''}$

The real part of the complex permeability corresponds to the normal permeability. The imaginary part, on the other hand, describes the magnitude of the magnetic reversal losses. ${\displaystyle {\mu _{\mathrm {s} }}'}$ ${\displaystyle {\mu _{\mathrm {s} }}''}$

With the exception of the ferromagnetic materials with a significantly higher relative permeability than one, the imaginary part of the complex permeability is also negligible, as is the frequency dependence of the permeability. The result is a scalar, frequency-independent permeability:

${\displaystyle \mu =\mu _{0}\cdot \mu _{\mathrm {r} }}$

In the case of ferromagnetic materials, the frequency dependency cannot be neglected for many technical applications, the result is:

${\displaystyle {\hat {\mu }}\,(f)={\mu _{\mathrm {s} }}'\,(f)-\mathrm {j} \cdot {\mu _{\mathrm {s} }}''\,(f)}$

where is the frequency of the alternating magnetic field. The imaginary part is directly assigned to the movement of the Bloch walls in the material and a resonance results in a maximum, usually in the range 10–1000 kHz. ${\displaystyle f}$ ${\displaystyle {\mu _{\mathrm {s} }}''(f)}$

Like many physical material properties, the complex permeability in its generalized linear form is actually a three-dimensional second order tensor . For most materials, however, the anisotropy of the magnetic properties is so small that a description as scalar, complex permeability is sufficient.

Classification

Permeability numbers for selected materials

medium	µ r	Classification
Superconductor type 1	0	ideally diamagnetic
Lead , tin	<1 (approx. 0.999 ...)	diamagnetic
copper	0.9999936 = 1 - 6.4 · 10 −6	diamagnetic
hydrogen	1 - 2.061 · 10 −9	diamagnetic
water	0.999991 = 1 - 9 · 10 −6	diamagnetic
vacuum	1	(neutral)
Polyethylene	~ 1	(neutral)
air	approx. 1 + 4 · 10 −7	paramagnetic
aluminum	1 + 2.2 · 10 −5	paramagnetic
platinum	1+ 2.57 · 10 −4	paramagnetic
cobalt	80 ... 200	ferromagnetic
iron	300 ... 10,000	ferromagnetic
Ferrites	4… 15,000	ferromagnetic
Mumetal (NiFe)	50,000 ... 140,000	ferromagnetic
amorphous metals (ferromagnetic)	700 ... 500,000	ferromagnetic
nanocrystalline metals (ferromagnetic)	20,000 ... 150,000	ferromagnetic

Magnetic materials can be classified based on their permeability number.

Diamagnetic substances  ${\displaystyle 0\leq \mu _{\mathrm {r} }<1}$

Diamagnetic substances have a slightly lower permeability than vacuum , for example nitrogen , copper or water . Diamagnetic substances tend to push the magnetic field out of their interior. They magnetize against the direction of an external magnetic field, consequently is . Diamagnetic contributions are generally independent of temperature. Type 1 superconductors are a special case . They behave like ideal diamagnets in a constant magnetic field . This effect is called the Meißner-Ochsenfeld effect and is an important part of superconductivity. ${\displaystyle \mu _{\mathrm {r} }<1}$ ${\displaystyle \mu _{\mathrm {r} }=0}$

Paramagnetic substances  ${\displaystyle \mu _{\mathrm {r} }>1}$

For most materials, the permeability number is slightly greater than one (for example oxygen , air ) - the so-called paramagnetic substances. In paramagnetic substances, the atomic magnetic moments align in external magnetic fields and thus strengthen the magnetic field inside the substance. So the magnetization is positive and therefore . The temperature dependence of the susceptibility is determined by Curies law . Paramagnetism can also have other causes, for example conduction electrons from metals make a temperature-independent contribution (Pauli paramagnetism). ${\displaystyle \mu _{\mathrm {r} }>1}$

Ferromagnetic substances  ${\displaystyle \mu _{\mathrm {r} }\gg 1}$

The ferromagnetic substances or soft magnetic materials ( iron and ferrites , cobalt , nickel ) are of particular importance , as these have permeability numbers of. These substances are often used in electrical engineering ( coil , electric motor , transformer ). Ferromagnets align their magnetic moments parallel to the external magnetic field, but do so in a strongly amplifying manner. In addition to ferromagnetic substances, ferrimagnetic and antiferromagnetic substances also have a magnetic order . ${\displaystyle 300\,000>\mu _{\mathrm {r} }>300}$

Differential permeability

In ferromagnetic materials, the magnetization does not generally depend linearly on the external magnetic field. It is possible to magnetize ferromagnetic materials to saturation. Because of this magnetic saturation and the magnetic remanence , the permeability is also not constant. For small fields, the permeability is significantly greater than near saturation. In addition, the magnetization depends on the previous magnetization, they are said to have a memory . The behavior is described by a hysteresis loop . The definition as a ratio only corresponds to the slope of the magnetization curve if it is linear. ${\displaystyle {\tfrac {B}{H}}}$

Different definitions of permeability are used depending on the application. For technical applications it is defined a total of eleven times with different calculations in DIN 1324 Part 2. In addition to the permeability as the quotient of the magnetic flux density in Tesla (T) and the magnetic field strength in amperes per meter (A / m), the differential permeability , i.e. the gradient of the hysteresis curve at one location, is used. ${\displaystyle \mu }$ ${\displaystyle B}$ ${\displaystyle H}$ ${\displaystyle \mu _{\mathrm {D} }}$

Hysteresis curve

The problem of constant assumed permeability can be seen from the hysteresis curve . The permeability corresponds to the slope ${\displaystyle \mu _{\mathrm {D} }}$

${\displaystyle \mu _{\mathrm {d} }={\frac {\mathrm {d} B}{\mathrm {d} H}}}$.

Anisotropy of permeability

In anisotropic materials, the magnetic permeability, like the electrical permittivity , is generally direction-dependent. This magnetic anisotropy can be described as a first approximation with a matrix or a permeability tensor. The components of the vectors and then depend on the equation ${\displaystyle \varepsilon }$ ${\displaystyle \mu _{ij}}$ ${\displaystyle B}$ ${\displaystyle H}$

${\displaystyle B_{i}=\sum _{i=1}^{3}\mu _{ij}H_{j}}$

together. The notation as tensor level 2 is only suitable to a limited extent to record the magnetic anisotropy of ferromagnetic materials. In particular, the crystalline anisotropy is non-linear. A definition analogous to that for differential permeability is necessary here. The permeability is a scalar material constant only in the case that linearity and isotropy are given .

See also

• Faraday scales

literature

• Hans Fischer: Materials in electrical engineering. Structure, properties, testing, application. 2nd revised edition. Carl Hanser Verlag, Munich et al. 1982, ISBN 3-446-13553-7 .
• Horst Kuchling: Pocket book of physics. 4th edition. Verlag Harri Deutsch, Thun et al. 1982, ISBN 3-87144-097-3 .
• Günter Springer: Expertise in electrical engineering. 18th completely revised and expanded edition. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 ( Europa-Lehrmittel 30318).
• Horst Stöcker (Ed.): Pocket book of physics. Formulas, tables, overviews. 4th corrected edition. Verlag Harri Deutsch, Thun et al. 2000, ISBN 3-8171-1628-4 .
• Physikalisch-Technische Bundesanstalt: The International System of Units (SI) . German translation of the BIPM brochure "Le Système international d'unités / The International System of Units (8e édition, 2006)". In: PTB-Mitteilungen . tape 117 , no. 2 , 2007 ( Online [PDF; 1.4 MB ]).

Individual evidence

1. ↑ permeable. In: Wissen.de. Retrieved May 29, 2017 . 
2. ^ Heinrich Frohne, Karl-Heinz Locher, Hans Müller: Moeller Fundamentals of Electrical Engineering . 19th edition. Springer-Verlag, 2013, ISBN 3-322-93889-1 , p. 224 ( limited preview in Google Book search).