magnetization

Physical size
Surname	magnetization
Formula symbol	${\displaystyle {\vec {M}}}$
Size and unit system unit dimension SI A · m -1 L −1 I ${\displaystyle \cdot }$

Simplified comparison of the magnetic flux density of
ferromagnetic (μ _f ),
paramagnetic (μ _p ) and
diamagnetic materials (μ _d )
to vacuum (μ ₀ )

The magnetization is a physical quantity to characterize the magnetic state of a material. It is calculated as the magnetic moment per volume : ${\displaystyle M}$ ${\displaystyle {\vec {m}}}$ ${\displaystyle V}$

${\displaystyle {\vec {M}}={\frac {d{\vec {m}}}{dV}}}$

The magnetization describes the relationship between the magnetic flux density and the magnetic field strength : ${\displaystyle {\vec {B}}}$ ${\displaystyle {\vec {H}}}$

${\displaystyle {\vec {B}}=\mu _{0}\left({\vec {H}}+{\vec {M}}\right)\ =\mu {\vec {H}}}$

Here is the magnetic field constant and the permeability . In diamagnetic materials , the magnetization is opposite to the generating field; in paramagnetic material , magnetization and field are directed in the same direction. ${\displaystyle \mu _{0}}$ ${\displaystyle \mu }$ ${\displaystyle \mu <\mu _{0}}$ ${\displaystyle \mu >\mu _{0}}$

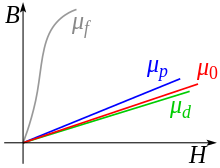
Also the - practically most important - ferromagnetic magnetization is directed in the same way as the field, but much larger than paramagnetic magnetization and not proportional to the field strength (see sketch on the right), i.e. H. is not a constant here, but depends on itself . A ferromagnetic body can be permanently magnetic . ${\displaystyle H}$ ${\displaystyle \mu }$ ${\displaystyle H}$

Every magnetization comes about through the alignment of elementary magnets. Since a body only contains a finite number of elementary magnets, there is a saturation magnetization that cannot be exceeded even in an external field of any strength. This is of great practical importance in ferromagnetism (see saturation ).

Description by the susceptibility

The magnetization can also be described by the magnetic field strength and the magnetic susceptibility : ${\displaystyle \chi _{\text{m}}}$

${\displaystyle {\vec {M}}=\chi _{\text{m}}\cdot {\vec {H}}}$

The susceptibility is dimensionless and can assume values ​​from −1 to almost infinite. The magnetization can therefore be opposite to the magnetic flux density.

Magnetization of a nail

Magnetization of a nail with the help of an external magnetic field

An iron nail, whose magnetic domains initially have random directions, can be magnetized by an external field . Domains change their direction and some domains enlarge at the expense of neighboring domains. Overall, this results in a magnetization that runs approximately parallel to the external field. This rearrangement of the magnetic domains can, for. B. be facilitated by external shocks or vibrations. Due to its ferromagnetic properties, the nail partially retains its magnetization even after the external field has been removed.

Magnetization in geology / mineralogy

Minerals and rocks can be permanently magnetized in various ways during their formation, whereby the earth's magnetic field determines the polarization:

• Thermally remanent magnetization (TRM): The magnetic alignment of the minerals in a melt is fixed by cooling below the Curie temperature .
• Chemically remanent magnetization (CRM): Minerals that become magnetizable minerals through a chemical reaction (e.g. oxidation , reduction ) align themselves during the conversion.
• Detritic remanent magnetization (DRM): During sedimentation in the water column, magnetizable mineral grains align themselves with the earth's magnetic field and are deposited with this alignment on the sediment .
• Postdetritic remanent magnetization (pDRM): Minerals align themselves with the deposition in the unconsolidated sediment.

literature

• Horst Stöcker: Pocket book of physics . 4th edition. Harri Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4 .
• Günter Springer: Expertise in electrical engineering . 18th edition. Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 .
• Hans Fischer: Materials in electrical engineering . 2nd Edition. Carl Hanser, Munich, Vienna 1982, ISBN 3-446-13553-7 .
• Horst Kuchling: Pocket book of physics . 4th edition. Harri Deutsch, Frankfurt am Main 1982, ISBN 3-87144-097-3 .

Web links

• Physical explanations of magnetization, magnetic fields and magnetism in general

Individual evidence

1. ^ Richard Feynman, Robert Leighton, Matthew Sands: The Feynman Lectures on Physics, Volume II . Addison-Wesley, 2006, ISBN 0-8053-9047-2 (Chapter 37: Magnetic Materials ).