alloy

In metallurgy, an alloy (from the Latin ligare ' to bind, to unite' ) is a macroscopically homogeneous metallic material made up of at least two elements (components), at least one of which is a metal and which together have the typical metal feature of metal bonding . From a chemical point of view, there are alloys that are mixtures and intermetallic compounds with a defined stoichiometric ratio of the metals involved. In general, alloys also have a crystalline structure. However, there are also amorphous metallic glasses .

Depending on the type of alloy formation, an alloy can be more homogeneous or heterogeneous at the microscopic level . Alloys that only form mixed crystals or exclusively intermetallic compounds are homogeneous. All others, which consist of several phases, are heterogeneous.

The behavior of the elements in an alloy and their influence on their properties are usually dependent on three factors: the type and number of alloy partners, their proportion by mass in the alloy and the temperature. These factors determine the respective absorption capacity, i.e. the solubility of one element in the other and whether the alloying partners form mixed crystals or mixtures of pure crystals (also crystal mixtures ) of the respective alloy components.

The verb alloy originally comes from the Latin ligare and means to bind together, to connect or to unite. In the 17th century , the now slightly modified legare (with the same meaning) was adopted into German .

properties

The alloying element can form a solid solution with the basic element (single-phase alloy) or several phases are formed . While the properties of single-phase alloys are essentially determined by the chemical composition, with multiphase alloys these are also significantly influenced by the distribution of the phases ( structure ). Base metal and alloying elements are also called components of an alloy. The list of alloying elements shows them and their effects on the respective base metals. Mixed crystals have a higher hardness and tensile strength , but a lower melting temperature than the base metal. In the case of metals, the electrical conductivity also drops . For the relatively soft, pure metals, solid solution strengthening is one of four possible strength-increasing processes to produce a hard material.

When a cast alloy solidifies, crystallization is not always complete. Certain alloys can also improve their mechanical properties (breaking strength, hardness, elongation) when they are cast - cold aged or heated - (“tempered”). In the case of wrought alloys , the recrystallization that strengthens the structure through cold aging or heat treatment is even a prerequisite for the manufacture of semi-finished products.

Examples of “natural alloys” are electrum , a gold - silver alloy, and stibarsen , an antimony - arsenic alloy.

In "man-made alloys", a distinction those that were deliberately made to material properties (Examples hardness , corrosion resistance) to change the "base metals" in the desired way, and those that are produced unintentionally as impurities ( metallurgy ) already by the Manufacturing can get into the alloy and have negative effects on the material properties. Examples of the latter are, inter alia, bismuth and / or arsenic in brass , as well as bismuth in AlSi alloys , where it severely affects the structure formation.

history

Copper, tin and bronze

Bronze axes

Copper is one of the first metals used by humans; it was discovered by chance about 6000 to 10000 years ago in charcoal fires that burned particularly hot when exposed to air. It gave the Copper Age its name. At a melting point of 1083 ° C, it can escape in liquid form from copper veins in the rock. By heating copper-containing, oxidic ores, however, copper can only be obtained with reducing firing, i.e. in the presence of charcoal. Also tin was discovered early, around 5000 years ago.

Bronze as an alloy of copper and tin (CuSn) is prehistoric since about 3300 v. Proven in Palestine . Bronze is harder and more edgy than copper and gave its name to an entire cultural epoch, the Bronze Age . Utensils, tools , weapons and jewelry were made from bronze. Many sculptures are still cast from bronze today.

Brass

Brass figure

Brass is an alloy of copper and zinc (CuZn). Zinc, mostly in the form of the zinc carbonate "calamine" ( Smithsonite ), has been around since the Bronze Age around 3000 BC. Used in Babylon and Assyria, in Palestine around 1400 to 1000 BC. Brass quickly became an important metal for coinage , but because of its beautiful, golden sheen, it was also used to make jewelry and sculptures.

Iron alloys

Iron sickle

Iron alloys were already used in prehistoric times , but only from meteorites , which often contain the iron-nickel (FeNi) alloy. Since meteorites were rarely found, iron objects were correspondingly valuable. The Sumerians called it "heaven metal", the ancient Egyptians "black copper from heaven". Smelted iron (recognized by the absence of nickel) was found in Mesopotamia , Anatolia and Egypt and is around 3000 to 2000 BC. BC originated. It was more valuable than gold and was mainly used for ceremonial purposes. Iron offered and still offers many advantages, the most important of which was the greater hardness compared to bronze and copper. Improvements in extraction and processing led people to make weapons first and then tools like plows out of iron. The Bronze Age was thus replaced by the Iron Age .

Classification

Depending on the number of components in the alloy, one speaks of a two-, three-, four- or multi-component alloy (binary, ternary, quaternary or polynary alloy), whereby only those components are counted that determine the characteristic properties. Since iron and steel are of particular importance in technology , alloys are divided into iron and non-iron alloys. Further classifications result from the type of alloy formation, as these arise not only from the melting of the components or from the special abilities of alloys.

• Natural alloys are created through the action of heat and the melting of elements, for example in the interior of celestial bodies . Since these alloys were not controlled by humans, they are not subject to their defined compositions and properties.
• Iron alloys are divided into cast iron and steel . The distinction is based on the carbon content . See main article iron-carbon diagram . Stainless steels are of particular importance: alloyed or unalloyed steels with a special degree of purity.
• Non-ferrous alloys (non-ferrous alloys; e.g. bronze , brass , amalgams , white gold , red gold ) are alloys based on non-ferrous metals .
• Diffusion alloys are created by the diffusion of atoms into the crystal lattice of the base metals. In particular, the first elements in the periodic table are able to migrate into its crystal lattice due to the small size of their atoms compared to the base metal . The best example of a diffusion alloy is the carburization of workpieces in order to harden them (see annealing ).
• Heusler's alloys are very special ferromagnetic alloys that do not contain iron, cobalt or nickel (example Cu ₂ AlMn).
• Shape memory alloys are metals that return to their original shape after being deformed by the action of heat.
• Cast alloys are used for direct shaping.
• Wrought alloys , as “semi-finished products”, are an intermediate product that is intended for further rolling, pressing or drawing forming.
• The workpieces produced by sintering ( pressing different, intimately mixed metal powders together at high temperature) are called pseudo-alloys . This process can also be used to mix elements that would not dissolve in one another in the molten state. Many tungsten alloys are z. B. made so.

Alloy formula

To identify an alloy, the base metal is usually mentioned first, followed by the most important component or components as an abbreviation for the metal with an appended number, which indicates the respective percentage ( mass percent ). An alloy CuZn37 (formerly known as brass 63 ) consists of the copper base to which 37% zinc has been added. In the case of the iron-carbon alloy steel, there are deviations from this system depending on the amount of alloying elements. In any case, iron is never specifically mentioned. For example, steel C37 contains 0.37% carbon and otherwise iron.

The specification of alloy proportions is based, among other things, on the DIN 1310 composition of mixed phases (gas mixture, solutions, mixed crystal); Basic terms regulated.

State diagram (state diagram, phase diagram)

During the thermal analysis , crystallization test series with different alloys of different composition are used to record the crystallization or crystal transformation points and enter them in a temperature-composition diagram, the temperature being dependent on the alloy composition.

For binary systems, three typical forms of state diagrams have emerged, especially with regard to the crystal system:

Two-component systems with complete solubility in the solid state

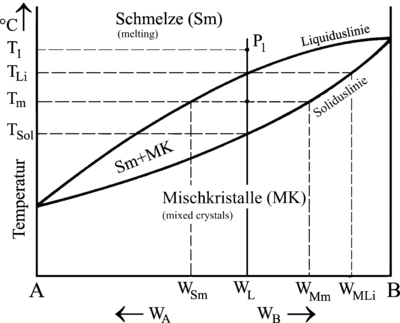
With complete solubility in the solid state, mixed crystals form in every composition. There are two ways of solid solution formation (MK), intercalation and substitution solid solution . Typical substitution MK formers are the alloys iron-chromium, iron-nickel, gold-copper, gold-silver and copper-nickel. Austenite (γ-iron-carbon) is an important intercalation MK-former .

In order for an alloy in any composition to be able to form mixed crystals with complete solubility in the solid state, the following requirements are necessary:

1. Both metals must have the same crystal system ( e.g. cubic ).
2. The lattice constants may differ by a maximum of about 15%.
3. The two metals must have a "certain chemical similarity".
4. The electronegativity difference must be "not too large".

Due to the mixed crystal formation, no matter how similar the alloy elements are, the crystal lattice is always distorted, since the different elements also have different atomic diameters. This creates tension; the sliding planes of the crystallites are prevented from yielding to deformations. So the lattice distortion increases the hardness.

A popular example of an alloy with complete solubility in the solid state is the two-component system Cu-Ni.

Cooling curves and state diagram of an alloy of different composition with solid solution formation

In contrast to the base metals (curves 1.6), the alloys (curves 2-5) do not solidify at a fixed temperature, but in a holding area. So the temperature does not stay constant, but slowly decreases. However, the holding ranges of different compositions of an alloy are always between the respective solidification temperatures of their pure components.

The reason for this is the "hindrance" of crystallization in an alloy by component A (curve 1), which, if it could, would solidify at an even lower temperature. Component B, on the other hand, “pushes” for solidification, which should actually have started earlier. This fact is also the reason why the crystals formed during the solidification change their mixing ratio and only when the cooling is slow enough ( thermal equilibrium ) until the end of the solidification, the desired mixing ratio is achieved by diffusion.

These compositions can be read from the state diagram by drawing a horizontal line through any point on the selected alloy (Figure W _L ) up to the solidus line . At the liquidus temperature T _Li (start of solidification) the first crystals therefore have a composition of W _MLi . The respective composition of the residual melt can also be determined in this way by, for example, drawing the horizontal line at T _m to the liquidus line. The melt would therefore have the composition W _Sm at this point and the mixed crystals would have the composition W _Mm .

With the aid of the state diagram and the law of levers, it can also be calculated how high the proportion of melt or the proportion of mixed crystals is at each intermediate temperature:

${\displaystyle M_{\mathrm {S} }\cdot W_{\mathrm {Sm} }+M_{\mathrm {MK} }\cdot W_{\mathrm {Mm} }=1\cdot W_{\mathrm {L} }}$ ${\displaystyle M_{\mathrm {S} }+M_{\mathrm {MK} }=1\ }$ ${\displaystyle M_{\mathrm {MK} }={\frac {W_{\mathrm {L} }-W_{\mathrm {Sm} }}{W_{\mathrm {Mm} }-W_{\mathrm {Sm} }}}}$ ${\displaystyle M_{\mathrm {S} }={\frac {W_{\mathrm {Mm} }-W_{\mathrm {L} }}{W_{\mathrm {Mm} }-W_{\mathrm {Sm} }}}}$

M S = proportion of melt W Sm = composition of melt (at T m ) M MK = proportion of mixed crystals W Mm = composition of mixed crystals (at T m ) W L = composition of alloy

Two-component systems with complete insolubility in the solid state

Alloys of this type are dissolved in one another in the melt, but separate completely during crystallization. The result is a crystal mixture of the pure components (see micrograph eutectic ).

Cooling curves and state diagram of an alloy of different composition with separate crystal formation

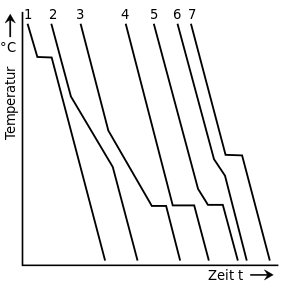
Even with separate crystal formation, alloys 2, 4 and 5 initially solidify in a holding area. Towards the end of solidification, however, the temperature curves describe a stopping point similar to that of a pure metal. Alloy 3 even solidifies exclusively in one stopping point.

The reason for this behavior is the strong, mutual hindrance of the two components, which separate during crystallization in order to be able to form crystals of their own kind. The maximum mutual interference is accordingly with alloy 3, in which crystals of components A and B simultaneously form at the solidification point. Due to the persistent mutual hindrance during separation and the low temperature, the paths of the atoms are very small and the crystal mixture is therefore very fine-grained.

Due to this peculiarity, alloy 3 is given the name Eutectic alloy (= the fine ; the well-built ). The solidus line common to all alloys is called the eutectical and the associated temperature is called the eutectic temperature (T _Eu ).

An outstanding example of a eutectic alloy with a particularly low melting point is Wood's alloy , whose melting point is 70 ° C.

In the case of alloys that are either to the left (= hypoeutectic) or right (= hypereutectic) of the eutectic, primary crystals of component A or primary crystals of component B solidify first. The proportion of primary crystals in an alloy can be calculated using the state diagram. The calculation starts at the point T _Eu , i.e. at the point where the residual melt has just reached the eutectic composition:

${\displaystyle M_{Eu}={\frac {W_{L}-W_{Pr}}{W_{Eu}-W_{Pr}}}}$ ${\displaystyle M_{Pr}={\frac {W_{Eu}-W_{L}}{W_{Eu}-W_{Pr}}}}$

M Eu = proportion of residual melt of eutectic composition = proportion of the eutectic M Pr = proportion of primary crystals W L = composition of alloy W Pr = composition of the primary crystals W Eu = composition of the eutectic

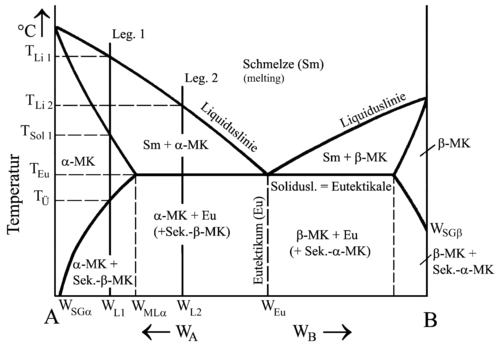
Two-component systems with limited solubility in the solid state

Alloys of this type can form mixed crystals, but not in every composition. In contrast to alloys with complete solubility, the atom sizes differ more strongly here, which means that the lattice distortions become unbearable above a certain composition. The crystal system can also be an obstacle if the alloying elements in the crystal system are similar but not the same.

For example, each component in the alloy lead (face-centered cubic) - tin (body-centered tetragonal) can form exchange mixed crystals with the other to a limited extent.

Typical MC-formers of limited solubility: aluminum-magnesium, lead-tin, copper-aluminum, copper-zinc, copper-tin, zinc-aluminum

Limited solubility in the solid state does not only mean that one component can absorb up to a certain percentage of atoms from the other component during crystallization, but also that the solubility decreases as the temperature falls. Since the kinetic energy of the atoms is lower, the lattice constant of the existing crystal system naturally also shrinks accordingly , and there is less space for foreign atoms. The consequence of this is that the mixed crystals begin to separate from the transition temperature T _Ü .

Precisely this property - partial segregation of the components due to decreasing solubility at lower temperatures - is exploited when hardening such an alloy. This is also referred to as precipitation hardening .

Cooling curves and phase diagram of an alloy of different composition with solid solution formation of limited solubility in the solid state

Alloy 1 thus solidifies from T _{Li 1} to T _{Sol 1} to form mixed crystals with the crystal system of A, called α-crystals. The homogeneous state is retained until T _Ü . The mixed crystals are saturated, which means that component A has absorbed component B up to the maximum solubility for this alloy.

At T _Ü, the atoms of B migrate to the grain boundaries according to the maximum solubility for this temperature and there form secondary mixed crystals with the crystal system of B, called β mixed crystals. To compensate for this, A atoms diffuse into the grain interior.

The proportion of secondary mixed crystals can be calculated using the following formula:

${\displaystyle M_{S\beta }={\frac {W_{S\alpha }-W_{L}}{W_{S\alpha }-W_{S\beta }}}}$ ${\displaystyle \left(M_{S\alpha }={\frac {W_{L}-W_{S\beta }}{W_{S\alpha }-W_{S\beta }}}\right)}$

M Sβ = proportion of secondary β mixed crystals W L = composition of alloy W Sβ = composition of secondary β mixed crystals W Sα = composition of secondary α mixed crystals M Sα = proportion of secondary α mixed crystals W Sα and W Sβ correspond at room temperature to W SGα and W SGβ (SG = saturation limit )

Alloy 2 initially crystallizes exactly like alloy 1. When the eutectical is reached, however, the residual melt solidifies at a break point and a fine-grained mixture of α and β mixed crystals is formed, which, as with separate crystal formation, is called a eutectic. The previously created α mixed crystals correspond to the primary crystals.

In this alloy, too, B atoms separate from the primary α mixed crystals below the eutecticals. In order to be able to calculate the proportion of secondary β mixed crystals from the primary crystals, the proportion of primary crystals in the overall alloy must first be calculated. The calculation corresponds to that for separate crystallization. Then the proportion of secondary β-mixed crystals is calculated from the primary crystals and multiplied by the proportion of primary crystals:

1) ${\displaystyle M_{Pr}={\frac {W_{Eu}-W_{L}}{W_{Eu}-W_{Pr}}}}$ ${\displaystyle \left(M_{Eu}={\frac {W_{L}-W_{Pr}}{W_{Eu}-W_{Pr}}}\right)}$ 2) ${\displaystyle M_{S\beta }={\frac {W_{S\alpha }-W_{\alpha }}{W_{S\alpha }-W_{S\beta }}}}$ 3) ${\displaystyle M_{LS\beta }=M_{S\beta }\cdot M_{Pr}}$

M Pr = proportion of primary crystals in% W Eu = composition of the eutectic W L = composition alloy W Pr = W MLα = composition of primary crystals (ML = miscibility gap ) M Sβ = proportion of secondary β mixed crystals (not in%) W Sα = composition of secondary α mixed crystals W α = Composition of primary α mixed crystals W Sβ = composition of secondary β mixed crystals M LSβ = proportion of secondary β mixed crystals in the alloy

Calculating the proportions of the secondary crystals in the eutectic does not make sense because they do not form a new phase here. Only atoms are regrouped while maintaining the crystal system. Therefore, no differences can be found either in the micrograph or in the technical properties.

Intermediate crystals

Another possibility for alloying is that the elements involved form a common crystal, but this does not resemble any crystal system of the basic elements. The result is its own crystal system, which, in contrast to those of pure metals, can be very complex. Such connections are also very hard and brittle. In addition, these crystals require a fixed atomic number ratio. An alloy with intermediate crystal formation , the alloying elements of which are exclusively metals, is called an intermetallic phase (with solubility for the constituent elements) or an intermetallic compound (with a stoichiometric composition). If such a phase occurs, a dystectic can be observed in the melting diagram .

Examples of intermediate crystallization are Al ₂ Cu, Mg ₂ Si, Cu ₄ Sn, Fe ₃ C ( cementite ) and WC ( tungsten carbide ).

The crystallization formula is similar to the formula for chemical compounds, which, in contrast to alloys, have a completely different type of compound .

Classification in the scheme of chemical substances

Schematic classification of the substances

material                                                                                                                               mixture                       Pure substance                                                                                               homogeneous mixture                         connection   element                                                                                           Gas mixture Mixture of several gases   Alloy Mixture with metallic properties , contains at least one metal   Solution Solid ,  liquid , gas dissolved  in a liquid             molecular   Ionic                                                       heterogeneous mixture                                                                                                                             Foam Gaseous bubbles in a liquid   Rigid foam Gaseous bubbles in a solid   Aerosol   Suspension Solid particles in a liquid   Emulsion Mixture of several immiscible liquids   Batch mixture of several not mixable solid                                                                             Smoke Solid particles in a gas   Fog Liquid particles in a gas

See also

• List of alloys
• List of alloying elements
• Master alloy

literature

• Stephan Hasse: Foundry Lexicon . Schiele & Schön, Berlin 1997, ISBN 3-7949-0606-3 (appendix from p. 1430 with numerous state diagrams of binary and ternary alloy systems).
• AF Holleman , E. Wiberg , N. Wiberg : Textbook of Inorganic Chemistry . 101st edition. Walter de Gruyter, Berlin 1995, ISBN 3-11-012641-9 .
• Alfred Böge: The Technician Handbook . 13th, revised edition. Vieweg, Braunschweig 1992, ISBN 3-528-14053-4 .
• Erhard Hornbogen: Materials . Springer, Berlin, Heidelberg, New York 2006, ISBN 3-540-30723-0 .
• Dieter Kohtz: Introduction to materials science for metal welders . In: Der Praktiker: the magazine for welding technology and more . 9/1982 to 1/1985. DVS-Verlag, ISSN  0554-9965 .
• Erwin Riedel: Inorganic Chemistry . de Gruyter, Berlin 2002, ISBN 3-11-017439-1 .
• Ulrich Müller: Inorganic Structural Chemistry . BG Teubner, Stuttgart 2004, ISBN 3-519-33512-3 .
• Wilhelm Domke: Materials science and material testing . 10th edition. Cornelsen, Düsseldorf 1987, ISBN 3-590-81220-6 .

Web links

Wiktionary: alloy  - explanations of meanings, word origins, synonyms, translations

• Surface alloys imaged with a scanning tunneling microscope

Individual evidence

1. ↑ Dieter Kohtz: Introduction to materials science for metal welders - What is an alloy . In: Der Praktiker: the magazine for welding technology and more . tape 1 . DVS-Verlag, 1984, ISSN  0554-9965 , p. 4 .
2. ↑ Lexicon of Physics: Alloys. Spektrum Akademischer Verlag, 1998, accessed January 27, 2018 .  
3. ↑ www.fremdwort.de: Alloy .
4. ↑ Friedrich Baumann: History of tin casting. (No longer available online.) Archived from the original on March 2, 2009 ; Retrieved April 2, 2009 .  
5. ↑ http://www.kupfer-institut.de/front_frame/frameset.php3?client=1&lang=1&idcat=27&parent=14 (link not available)
6. ^ Marianne Schönnenbeck, Frank Neumann: History of zinc. Rheinzink , accessed on March 26, 2018 ( complete report as eBook ).  
7. ↑ Helmut Föll: History of steel. In: Introduction to Materials Science I. Accessed April 2, 2009 .  

This version was added to the list of articles worth reading on October 25, 2005 .