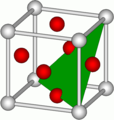
Sliding system

The sliding system in describing crystal mechanics means of sliding plane and sliding the deformation of metals by dislocation movement .

In the case of plastic deformation , those dislocations are moved in whose sliding system the maximum shear stress prevails. The shear stress acting on a sliding system is determined by the orientation of the sliding system to the applied stress ( Schmid's law of shear stress ). The dislocation movement generates further dislocations which, as obstacles, make the dislocation movements more difficult. As a result, hardening is observed in most metallic materials .

As the deformation progresses, the crystal lattice rotates until the maximum shear stress acts in another sliding system and this takes over the further deformation of the crystal. The tension required for this will generally be higher than in the first active sliding system, which represents a further contribution to the hardening.

Slip plane

The slip planes in a crystal form the planes between atomic layers with the closest packing and large layer spacing. The dislocation movement takes place in them when they are deformed, since the relatively smallest critical shear stress is required.

Slip planes are marked with the Miller indices commonly used in crystallography . Typical examples are the {111} plane in the face-centered cubic lattice and the {110} and {112} planes in the body-centered cubic lattice. In the hexagonal crystal system , {0001} is usually the slip plane.

• 

  {111} sliding plane in a face-centered cubic lattice

• 

  {110} sliding plane in a body-centered cubic lattice

Structure of two isomorphic TCNQ - complex salts, drawn by coordinates of Table: McPhail AT, GM.Semeniuk, DBChesnut, J. Chem. Soc. (A) (1971) p. 2174

In molecular crystals with a complicated structure, the sliding systems can also be based on other selection rules. In the case of two isomorphic triclinic TCNQ complex salts, it was found that the slip plane (010) is oriented parallel to a kind of alley in the structure which is not crossed by parts of the molecules, so that slip in the slip directions [ ], [ ] and their Opposite directions can take place without the molecules themselves being damaged. ${\displaystyle 101}$ ${\displaystyle 10{\bar {1}}}$

Sliding direction

The sliding direction is the direction of the densest atomic packing and thus the direction in which the sliding of the atomic layers is possible with a relatively low expenditure of energy .

Typical examples are

• in the face-centered cubic lattice the <110> direction
• in the body-centered cubic lattice the <111> direction
• in the hexagonal crystal system mostly the <1120> direction.

Sliding systems of the most important crystal structures

Different possible sliding systems result from the possible sliding planes and sliding directions.

Crystal structure	Slip plane	Sliding direction	non-parallel planes	Sliding directions per level	Number of sliding systems	annotation
vehicle	{111}	<110>	4th	3	12
short	{110}	<111>	6th	2	12
	{112}	<111>	12	1	12
	{123}	<111>	24	1	24	not found in all krz metals
hex	{0001}	<1120>	1	3	3
	{1010}	<1120>	3	1	3	not active in all hex metals
	{1011}	<1120>	6th	1	6th	not active in all hex metals

The different sliding systems also explain the different deformability of the crystal structures: In vehicle and vehicle structures, systems of the same type are spatially evenly distributed. In contrast, in hex structures, the easily activated {0001} <1120> systems allow movement in only one plane; therefore, the contribution of the other sliding systems (or the mechanical twin formation ) is always necessary for any deformation , but this usually requires a significantly higher tension.

literature

• G. Gottstein: Physical basics of metallurgy . 3. Edition. Springer, Berlin 2007, ISBN 978-3-540-71104-9 .
• Gustav ER Schulze: Metal Physics . 2nd Edition. Springer, Vienna 1974, ISBN 3-211-81113-3 .

Individual evidence

1. ↑ Heinz HW Preuß: Trikline TCNQ complex salts as a model body for the investigation of crystal plasticity with low symmetry, Dissertation B (habilitation thesis) Leipzig, 1977 . In: Freiberg research booklet . B 204. VEB Deutscher Verlag für Grundstofftindustrie, Leipzig 1978.
2. ↑ damask.mpie.de/Documentation/FCC , overview of all systems and spherical model.
3. ↑ damask.mpie.de/Documentation/BCC , overview of all systems and spherical model.
4. ↑ damask.mpie.de/Documentation/hex , overview of all systems and spherical model.