Miller indices

Selection of Miller indices in a cube

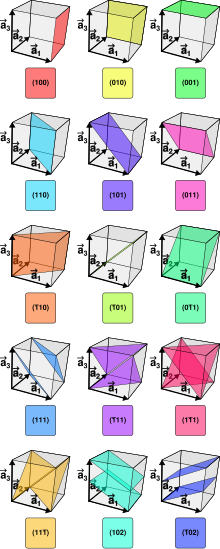
Miller's indices are used in crystallography to clearly designate crystal faces or planes in the crystal lattice. The spelling (hkl) was proposed in 1839 by William Hallowes Miller (1801-1880). In the same work Miller also introduced the notations in use today [uvw] for directions (direction indices) and {hkl} for crystal forms , i.e. H. the set of all symmetrically equivalent surfaces.

The Miller indices are formed as follows: The points of intersection of the crystal plane with the three coordinate axes are determined, common factors are abbreviated, the reciprocal values ​​are formed and multiplied by the lowest common multiple of the denominator, so that three whole, relatively prime numbers result.

Applications

In mineralogy , Miller indices are used to clearly describe crystal faces . They are also required for specifying the cleavage or twinning .

In diffraction methods such as X-ray diffraction or electron diffraction , they designate a lattice plane . Higher indices - for example 222 - are also used here to indicate the higher order diffraction. These indices are known as Laue indices or Laue symbols . They are usually written without brackets to distinguish them from Miller indices, which are coprime by definition. Laue indices are z. B. used when specifying systematic extinctions and are included in the formula of the structure factor. The Laue indices are the Miller indices multiplied by the order n of the interference (see Bragg equation ), e.g. B. the 2nd order reflection at the lattice plane with the Miller indices (100) is denoted by Laue indices 200.

In materials science , both lattice planes and lattice vectors are needed to characterize lattice defects such as dislocations . Also, sliding systems , textures or the crystal orientation of single crystals can be described by Miller indices.

notation

Depending on its crystal system , each crystal is assigned a coordinate system. The three vectors , and may form the basis of this grid coordinate system (not to be confused with the primitive translations of the grid). The basis of the associated reciprocal lattice is given by the vectors , and (they are defined by the basis vectors of the lattice). ${\displaystyle {\vec {a_{1}}}}$ ${\displaystyle {\vec {a_{2}}}}$ ${\displaystyle {\vec {a_{3}}}}$ ${\displaystyle {\vec {g_{1}}}}$ ${\displaystyle {\vec {g_{2}}}}$ ${\displaystyle {\vec {g_{3}}}}$ ${\displaystyle {\vec {a_{i}}}}$

Lattice plane (Miller indices)

The Miller indices are three integer , relatively prime indices , and , which form the number triplet . Negative indices are marked with a bar written over the number, for example . Each such triplet denotes a specific plane. ${\displaystyle h\!\,}$ ${\displaystyle k\!\,}$ ${\displaystyle l\!\,}$ ${\displaystyle (hkl)\!\,}$ ${\displaystyle ({\bar {1}}0{\bar {2}})\!\,}$

If all symmetrically equivalent levels are meant instead of a specific network level, the notation is used. For example, referred to the cubic crystal system the equivalent due to the cubic symmetry planes , , , , and what the six surfaces of a cube equivalent. ${\displaystyle \{hkl\}\!\,}$ ${\displaystyle \{100\}\!\,}$ ${\displaystyle (100)\!\,}$ ${\displaystyle ({\bar {1}}00)\!\,}$ ${\displaystyle (010)\!\,}$ ${\displaystyle (0{\bar {1}}0)\!\,}$ ${\displaystyle (001)\!\,}$ ${\displaystyle (00{\bar {1}})\!\,}$

Each set of lattice planes in the direct lattice corresponds to a point or position vector in the reciprocal lattice of the crystal. This vector has the coordinates in reciprocal space ; it is always perpendicular to the network level of the same name and its length is the reciprocal of the network level distance. ${\displaystyle (hkl)\!\,}$ ${\displaystyle h,k,l\!\,}$

There are two equivalent possibilities to describe a grid plane :

Lattice level in the local area

If one considers a grid plane with the trace points , and , ( are the unit vectors of a right-angled coordinate system of the space), the intercept form is given by: ${\displaystyle s_{1}{\vec {e_{1}}}}$ ${\displaystyle s_{2}{\vec {e_{2}}}}$ ${\displaystyle s_{3}{\vec {e_{3}}}}$ ${\displaystyle {\vec {e_{i}}}}$

${\displaystyle {\frac {1}{s_{1}}}x_{1}+{\frac {1}{s_{2}}}x_{2}+{\frac {1}{s_{3}}}x_{3}=1}$

Here is

${\displaystyle {\vec {n}}={\begin{pmatrix}{\frac {1}{s_{1}}}\\{\frac {1}{s_{2}}}\\{\frac {1}{s_{3}}}\end{pmatrix}}}$

a normal vector of the plane. Now form a multiple of this normal vector so that all entries of this multiple of the normal vector are whole coprime numbers. Let this be B. guaranteed in the following by the whole number (possible because the , since the intersection points should lie on the crystal lattice), then applies ${\displaystyle j}$ ${\displaystyle s_{i}\in \mathbb {Z} }$

${\displaystyle {\vec {n_{2}}}={\begin{pmatrix}{\frac {j}{s_{1}}}\\{\frac {j}{s_{2}}}\\{\frac {j}{s_{3}}}\end{pmatrix}}={\begin{pmatrix}h\\k\\l\end{pmatrix}}}$

The components of the tuple are called the Miller indices. Negative numbers are indicated by a line above the corresponding index instead of the minus sign. An index of zero denotes an intersection at infinity (as you can see from the intercept form), i.e. that is, the corresponding basis vector is parallel to the plane. ${\displaystyle (hkl)\!\,}$

Lattice plane in the reciprocal lattice

The other option is with the reciprocal lattice vector ${\displaystyle (hkl)\!\,}$

${\displaystyle h{\vec {g_{1}}}+k{\vec {g_{2}}}+l{\vec {g_{3}}}}$

to call. This vector is perpendicular to the corresponding grid planes.

The whole numbers , and are used that no longer have a common factor. This corresponds to the shortest reciprocal lattice vector that is perpendicular to the plane. ${\displaystyle h\!\,}$ ${\displaystyle k\!\,}$ ${\displaystyle l\!\,}$

Lattice vectors (direction indices)

Vectors within the grid can also be designated by indices. The notation is used to denote a specific vector. The notation denotes all directions symmetrically equivalent to the vector . ${\displaystyle [uvw]\!\,}$ ${\displaystyle \langle uvw\rangle \!\,}$ ${\displaystyle [uvw]\!\,}$

Examples: In the case of a cubic crystal (i.e. a cube), one direction is parallel to one of the cube edges, the direction of one of the surface diagonals and the direction of a spatial diagonal. ${\displaystyle \langle 100\rangle \!\,}$ ${\displaystyle \langle 110\rangle \!\,}$ ${\displaystyle \langle 111\rangle \!\,}$

The notation describes a vector in the real grid (grid vector ) ${\displaystyle [uvw]\!\,}$

${\displaystyle u{\vec {a_{1}}}+v{\vec {a_{2}}}+w{\vec {a_{3}}}.}$

This vector is generally not perpendicular to the plane . This is only the case in the cubic lattice . ${\displaystyle (uvw)\!\,}$

Quadruple notation

Miller indices in the hexagonal crystal system

In the trigonal crystal system and in the hexagonal crystal system , the notation with four indices is often used. These modified Miller indices are referred to as Bravais indices (also Bravais-Miller indices or Miller-Bravais indices ). An advantage of these indices in the hexagonal crystal system is that symmetry-equivalent faces are easy to identify, since they are obtained by permutating the first three indices. Such are the surfaces , and, for example, surfaces of the hexagonal prism. The indices , and agree with the usual Miller indices, always results as . ${\displaystyle (HKIL)\!\,}$ ${\displaystyle (10{\bar {1}}0)\!\,}$ ${\displaystyle (01{\bar {1}}0)\!\,}$ ${\displaystyle (1{\bar {1}}00)\!\,}$ ${\displaystyle H\!\,}$ ${\displaystyle K\!\,}$ ${\displaystyle L\!\,}$ ${\displaystyle I\!\,}$ ${\displaystyle -(H+K)\!\,}$

There is also a four-way notation for the direction indices. In crystallography and mineralogy, the normal directional indices or are mostly used, whereby a placeholder for indicates that the trigonal or hexagonal crystal system is meant. t is always zero. However, this notation is sometimes used for the Weber indices described below , which can lead to confusion. ${\displaystyle [uv.w]}$ ${\displaystyle [uv^{*}w]}$ ${\displaystyle t}$

In materials science, a different spelling is preferred, the so-called Weber indices or Weber symbols . The conversion from the three-way notation differs here from the conversion of the level indices: ${\displaystyle [UVTW]\!\,}$ ${\displaystyle [uvw]\!\,}$

${\displaystyle U=(2u-v)/3}$

${\displaystyle V=(2v-u)/3}$

${\displaystyle T=-(u+v)/3}$

${\displaystyle W=w.}$

The advantage of this notation is that the direction is perpendicular to the plane, similar to that in cubic crystal systems . In the three-way notation this is generally not the case in these crystal systems. In addition, as with the Miller-Bravais indices in cubic crystal systems, for reasons of symmetry, equivalent directions can be obtained by permutating the first three indices, and one means that the direction is perpendicular to the corresponding basis vector. Since the conversion of directions into the four-way notation is more complicated compared to planes, directions with Weber indices are often given incorrectly in the literature. ${\displaystyle [UVTW]\!\,}$ ${\displaystyle (UVTW)\!\,}$ ${\displaystyle 0}$

Derivation

The direction is supposed to be equivalent , i.e. H. both indices should point in the same direction. So is ${\displaystyle [uvw]}$ ${\displaystyle [UVTW]}$

${\displaystyle u\cdot {\vec {a}}+v\cdot {\vec {b}}+w\cdot {\vec {c}}\propto U\cdot {\vec {a}}+V\cdot {\vec {b}}+T\cdot {\vec {d}}+W\cdot {\vec {c}}.}$

Now is

${\displaystyle {\vec {d}}=-({\vec {a}}+{\vec {b}}),}$

which is why this turns out to be

${\displaystyle u\cdot {\vec {a}}+v\cdot {\vec {b}}+w\cdot {\vec {c}}\propto (U-T)\cdot {\vec {a}}+(V-T)\cdot {\vec {b}}+W\cdot {\vec {c}}}$

lets write. There

${\displaystyle T=-(U+V)}$

holds, follows

${\displaystyle u\cdot {\vec {a}}+v\cdot {\vec {b}}+w\cdot {\vec {c}}\propto (2U+V)\cdot {\vec {a}}+(2V+U)\cdot {\vec {b}}+W\cdot {\vec {c}}}$.

Therefore, the conversion of Weber symbols into directional indices is based on the three-way notation

${\displaystyle u=2U+V}$

${\displaystyle v=U+2V}$

${\displaystyle w=W,}$

but it has to be shortened at the end. The latter equations can be obtained by solving for , and the equations for determining the Weber indices from the three-way notation. ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle W}$

literature

• Charles Kittel : Introduction to solid state physics. 7th ed. Wiley, New York 1996. ISBN 0-471-11181-3 .
• Werner Schatt, H. Worch: Material Science. 8th edition Ger. Verl. Für Grundstofftindustrie, Stuttgart 1996. ISBN 3-342-00675-7 .
• Hans-Joachim Bautsch , Will Kleber , Joachim Bohm : Introduction to crystallography . Oldenbourg Wissenschaftsverlag, 1998 ( limited preview in Google book search).
• Christopher Hammond: The basics of crystallography and diffraction . Oxford University Press, Oxford 2001, ISBN 978-0-19-850552-5 ( limited preview in Google Book Search).

Web links

Commons : Miller Index  - album of pictures, videos and audio files

• IUCr Online Dictionary of Crystallography: Miller indices
• IUCr Online Dictionary of Crystallography: Bravais-Miller indices
• Directions and levels in the grid at Kiel University
• Video lecture at the University of Tübingen

Individual evidence

1. ↑ William Hallowes Miller : A treatise on crystallography . Deighton, Cambridge 1839, LCCN  04-030688 , OCLC 8547577 (English, full text in the Google book search).
2. ↑ Walter Borchardt-Ott: Crystallography. Springer 2008, p. 285, footnote 3.
3. ↑ Wolfgang Demtröder: Experimental Physics 3: Atoms, Molecules and Solids . Springer, 2005, ISBN 3-540-21473-9 , pp. 386 ( limited preview in Google Book Search).
4. ↑ Leonhard Weber : The four-part zone symbol of the hexagonal system . In: Z. Kristallogr. tape 57 , 1922, pp. 200-203 .
5. ^ Christopher Hammond, The Basics of Crystallography and Diffraction . Oxford University Press, 2001, ISBN 978-0-19-850552-5 , pp. 115 ( limited preview in Google Book search).