X-ray diffraction
X-ray diffraction , and X-ray diffraction ( English X-ray diffraction called XRD), the diffraction of X-rays of ordered structures such as crystals or quasi-crystals . X-rays basically show the same diffraction phenomena as light and all other electromagnetic waves . X-ray diffraction is used in materials physics, crystallography , chemistry and biochemistry to study the structure of crystals, known as X - ray diffractometry . For example, X-ray scattering results played an important role in structural analysis of DNA . The devices used for this purpose were originally X-ray cameras that recorded diffraction images on commercially available X-ray films; today, X-ray diffractometers with counter tubes, area detectors or the like are mainly used.
history
The phenomenon of X-ray diffraction on crystals was postulated in 1912 by Max von Laue after a conversation with Paul Peter Ewald and confirmed by the experiments of Walter Friedrich and Paul Knipping . For this, von Laue received the Nobel Prize in Physics in 1914 . Since diffraction is a typical property of waves , he was able to prove the wave nature of X-rays. Up to this point in time, it was not yet certain whether the radiation discovered by Wilhelm Conrad Röntgen in 1895 was a matter of waves or particles. Today we know that X-rays are light with wavelengths beyond UV radiation and that this has both particle and wave properties (see wave-particle dualism ). Based on the work of Max von Laue, William Henry Bragg and William Lawrence Bragg (father and son) began to use X-ray diffraction as a method for determining the structure of crystals in 1913 . Among other things, they succeeded in clearing up the crystal structures of NaCl , diamond , zinc blende , fluorspar and calcite . For this work both received the Nobel Prize in Physics in 1915. X-ray diffraction is still one of the standard methods for determining the structure of solids today.
Applications
The possible uses of X-ray diffraction are diverse. In addition to applications in research, X-ray diffraction methods are routinely used in the metal and building materials industry, the pharmaceutical industry or geological exploration, and in some cases fully automated, for sample analysis or production monitoring. Possible applications of X-ray diffraction include:
- Phase analysis: the qualitative or quantitative determination of crystalline phases based on their diffraction pattern, including the determination of minerals
- Determination of the lattice parameters (lattice constants)
- Crystal structure analysis : the determination of the symmetry ( space group ) and the crystal structure determination in the narrower sense, i.e. the determination of the atomic positions within the unit cell
- X-ray stress determination (RSE): Investigation of the strain and stress state of a material
- Texture analysis : the determination of the orientations ( orientation density distribution function) of the crystallites in a multicrystalline solid
- Determination of the crystal orientation in single crystals
- Investigations on thin layers
For many of these applications, synchrotron radiation , neutron radiation or electron radiation are used today in addition to classic X-rays .
Physical background
Diffraction occurs when the distance between the grating lines of the diffraction grating is of the order of magnitude of the wavelength of the incident waves. The wavelength of X-rays is in the order of 1 pm to 10 nm, which corresponds to the distance between the atoms in crystals. Therefore they act like a three-dimensional diffraction grating on X-ray light.
The X-rays are bent at the electron shell of the irradiated atoms (with neutron radiation, this happens at the nucleons). The diffracted waves emanating from the individual atoms interfere with one another. Depending on the distance between the atoms, there are different path differences for the diffracted waves . Whether there is constructive or destructive interference at a fixed angle therefore depends on the distance between the atoms.
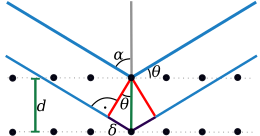
Since crystals consist of three-dimensional and periodically arranged structural units, constructive interference occurs only for very specific angles. These angles can be related to the distance between certain lattice planes of the crystal using the Bragg equation described below . The mosaic structure of the crystal is a necessary condition for X-ray diffraction .
An alternative to the Bragg description is the Von Laue description. There one does not assume scattering at network planes, but rather scattering at individual microscopic objects (see main article Laue condition ). Both descriptions are equivalent, although they are based on different assumptions.
Another possibility of performing X-ray diffraction is the direct generation of X-rays in the crystal by exciting the atoms by bombarding them with high-energy particles (e.g. electrons). Nothing changes in the description of diffraction by the Bragg or Laue description. This is known as the Kossel effect .
Bragg equation
The Bragg equation is the underlying mathematical relationship for determining the structure from the diffraction image obtained during X-ray diffraction:
Here, the wavelength of the monochromatic X-ray beam irradiated with the one sample, the spacing of the lattice planes , the angle to the network level, below the incident radiation and the degree of the examined peak from the center, counted in the form of a natural number.
The equation describes the conditions for constructive interference. The right side of the Bragg equation describes the path difference between two X-rays diffracted at two lattice planes with the distance . If this is an integral multiple of the wavelength, constructive interference occurs. William Lawrence Bragg described this equation as a “reflection condition”, since macroscopically the impression arises that the X-ray radiation is reflected by the crystal at the angle .
If the Bragg equation is fulfilled for a family of parallel network planes, the waves “reflected” by the individual planes are superimposed in such a way that constructive interference occurs. For each set of lattice planes, there are only certain angles at which reflection takes place. These angles are called glancing angles or Bragg angles.
The radiation caused by constructive interference can be registered by a detector or a photo film. The angle of deflection of the waves resulting from constructive interference from the incident beam is . Since the wavelength of the X-ray radiation used is known, the lattice plane spacing can be calculated, where hkl are the Laue indices that indicate the position of the set of parallel lattice planes in the crystal lattice and at the same time the order of diffraction.
If the crystal system is known, the lattice constants of the crystallographic unit cell can be derived from it.
In the cubic crystal system , for example:
- .
If one has calculated, the lattice constant of the unit cell can be calculated by assigning the reflections to individual lattice planes (i.e. to hkl reflections) .
The following applies to a rhombic crystal system :
- .
If d is known, the lattice constants a, b and c are calculated using approximation methods. You have to proceed in a similar way for other crystal systems.

As already mentioned, the different spacing between the lattice planes results in X-rays that interfere with one another. When entering the crystal, the individual X-rays are in phase. Due to the diffraction, however, there is interference and a shift of the individual phases from one another, one speaks of phase relationships. The Bragg equation shows the condition for constructive interference. The phase relationship is thus a shift in the phases of two waves by exactly one integer value. Destructive interference results when the phases are shifted by non-integer values.
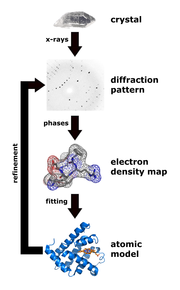
With detectors for X-rays, only the intensity of the radiation can be measured. Constructive or destructive interference can be inferred from appearing reflexes or systematic extinctions. However, all other phase relationships that carry the actual information for the distribution of the electron density in the crystal are lost. This dilemma is known in X-ray structure analysis as the phase problem .
The structure factor is the total resultant of all waves diffracted in one direction of a -reflection. The measured intensity is proportional to the square of the structure factor ,
and the structure factor is the Fourier transform of the electron density
- ,
where represent the lattice constants, the coordinates in the unit cell and the Laue indices. The positions of the atoms in the unit cell correspond to the positions of the electron density maxima; Hydrogen atoms, in which the maximum electron density lies on the bond to the neighboring atom, are the only exception.
The measured intensities only have information about the amplitude, i.e. the amount of the structure factor. In order to derive the structure factors from the intensities, the phase problem must therefore be solved. Today the “direct methods” are mostly used for the development of which Herbert A. Hauptman and Jerome Karle received the Nobel Prize in Chemistry in 1985. Another important method for solving the phase problem is the Patterson method , which is mainly used in the presence of heavy atoms.
In practice, Fourier methods are rarely used. Instead, one uses structure refinement. The structure factor can also be expressed as the sum of all atomic scattering factors of the atoms in the unit cell:
- ,
where all atoms in the unit cell are summed, representing the coordinates of the atom and the Miller indices. The atomic scattering factor is the Fourier transform of the electron density of an atom. Usually the electron density of a spherical atom is assumed, which does not overlap with its neighboring atoms. With the help of this sum equation, the structure factor can be calculated from the coordinates of the atoms in the unit cell. In the structure refinement, the structure model (the atomic coordinates) is changed until the difference between the experimentally measured structure factors and the structure factors calculated from the model is minimal. The method of least squares is used to refine structures with computer programs .
Atoms in the crystal lattice swing around their rest position. Because this also has an effect on the reflection intensities, the atomic scattering factors for the thermal movement are corrected. The structural model therefore consists of spherical atoms that oscillate (harmoniously) around their rest position. See Debye-Waller factor .
Procedure
The oldest diffraction method are the Laue method (1912), the Bragg spectrometer method (1913), the powder diffraction (1916) and the crystal rotation method , which according to the first approach of de Maurice Broglie of Michael Polanyi and Karl Weissenberg and independently of which was developed by Ernst Schiebold . From these four original methods a large number of other methods and devices emerged, which can be classified according to the following criteria: radiation used (“white” or monochromatic), sample (single crystal or powder) and detector (film or counter tube).
| radiation | sample | detector | Procedure |
|---|---|---|---|
| White | Single crystal | Movie | Laue camera |
| Counter tube ( ionization chamber ) | Bragg spectrometer | ||
| monochromatic | Single crystal | Movie |
Rotational crystal camera , panning shots ( oscillating camera ) Weissenberg camera De Jong-Bouman camera precession camera |
| Counter tube, also area detectors | Single crystal diffractometer | ||
| monochromatic | powder | Movie | Debye-Scherrer camera Guinier camera Seemann-Bohlin camera Gandolfi camera |
| Counter tube |
Powder diffractometer (mostly Bragg-Brentano diffractometer ) Guinier diffractometer |
Laue method
In the Laue process, a single crystal is exposed to polychromatic X-rays. The idea is to satisfy the Bragg equation by varying the wavelengths. However, the reflections obtained in the diffraction image cannot be clearly assigned to individual lattice plane distances. It is still used today to study dynamic processes, for example in protein crystals .
Rotary crystal process
An evaluation of the Laue method for determining according to the Bragg equation is hardly possible. The lattice constants cannot be determined either. In the rotating crystal method, the single crystal to be examined is rotated around a zone axis perpendicular to the primary beam. The evaluation of the rotating crystal image makes it possible to determine the lattice constants.
Weissenberg method
This process is a further development of the rotary crystal process. For this purpose, a cylindrical slice line aperture is inserted into the camera between the crystal and the film. The effect of this is that only the rays of a cone whose opening angle can be adjusted by moving the aperture can expose the film. In addition, the crystal rotation is synchronously coupled with a linear displacement of the cylindrically rolled film (e.g. 1 ° crystal rotation corresponds to a film movement of 1 mm). This pulls the reflections apart in the film plane, making it easier to determine the indices of the individual reflections. Instead of the primary spot in the rotary crystal image, the Weissenberg image shows a center line from which two coordinates can be assigned to each reflection.
Two similar processes, in which the film is not shifted, but rotated around the axis of the primary beam, are the processes of Erwin Sauter and Ernst Schiebold . In contrast to the Weissenberg process, these two processes, which are often grouped under the name of the Schiebold-Sauter process , have rarely been used in practice.
Debye-Scherrer method
The method developed by Peter Debye and Paul Scherrer and independently by Albert W. Hull does not work with single crystals but with powder samples. The powder consists of a series of randomly arranged crystallites, so that the lattice planes are also randomly arranged in space and some of them always meet the Bragg reflection condition. In addition, the sample rotates around an axis perpendicular to the incident beam. Conical shells from X-rays, which originate from the constructive interference, form around the sample. Around the sample is a photographic film on which the cone shells can be seen as reflections from which the diffractogram can then be created. The glancing angle can be calculated from the distances between the reflections recorded by the incident beam on the film :
- .
The distance of the diffraction reflex on the film from the incident beam is related to the circumference of the camera like the opening angle of the corresponding diffraction cone to 360 °.
Guinier method
This procedure is similar to the Debye-Scherrer procedure . In a circular chamber, however, the sample is not attached in the middle, but like the film on the chamber wall. It can be shown that any ray that traverses the chamber and is focused on the same point on one wall is imaged on the same point on the circumference when diffracted on the other wall. In this way, an X-ray beam can be used that is not parallelized, but only focused by grazing incidence into a concave mirror . This means that the intensity of an X-ray source can be used much better with simple means.
The chamber can be used to produce radiographic and retro-reflective images. As with the Debye-Scherrer method, the distance between the reflections on the film is directly proportional to the diffraction angle. The diameter of the chamber is usually 114.7 mm. When measuring the diffraction pattern on the film, 1 mm then corresponds to exactly 0.5 °. With this method you get more sharply mapped diffraction rings. In addition, three preparations in powder form can be recorded at the same time, whereby two preparations with a calibration substance , which is shown on the film in the middle area, are usually recorded.
Counter tube process
In modern powder diffractometers , unlike in the previous methods, a scintillation counter is used instead of a film to register the diffracted X-rays , which has the function of a counter tube. With this method, the interference intensity can be determined directly with high accuracy. Another advantage is the digital evaluation, so that many work steps can be automated.
Single crystal diffractometers use either such a point detector or an area detector (CCD, CMOS, Imageplate), which can measure the intensity and shape of several reflections at the same time.
Other methods
A special form of X-ray scattering is the small angle scattering (engl. Small angle X-ray scattering , SAXS): Da according to the Bragg equation at a given wavelength larger structures have a smaller scattering angle result, the small-angle scattering may be used to mesoscopic structures such as colloids to investigate partially crystalline polymers and the like. SAXS is one of the standard methods for structure elucidation in soft matter physics.
Another form of X-ray scattering is WAXS ( wide angle X-ray scattering ).
X-ray tubes and synchrotrons serve as X-ray sources . As an alternative (and in addition) to X-ray scattering, neutron scattering and electron diffraction are used. The advantage of structure determination with synchrotron radiation lies in the high intensity and excellent vertical collimation . The evaluation of powder data is made much easier by the higher resolution.
X-ray diffraction with grazing incidence is particularly suitable for thin layers .
With AXS ( anomalous X-ray scattering ), the contrast between several elements contained in the sample can be increased in X-ray scattering experiments . This makes use of the fact that the form factor of an element has a pronounced dependency on the wavelength of the incident radiation when this is in the immediate vicinity of an absorption edge of that element. Using this technique, additional information can be obtained on elements that would contribute little to the scattered intensity in a regular scattering experiment because 1. the element in question has a lower atomic number than other sample components, or 2. because the concentration of the element in the sample is very high is low. Since the wavelength of the radiation has to be varied for AXS and the effects to be observed are weak, synchrotron radiation is mostly used for such measurements.
X-ray diffraction in liquids
If one observes sharp reflections in solid crystalline substances, which occur at very specific glancing angles and can be traced back to the lattice planes in the crystal, the diffraction diagram of liquids in the intensity distribution shows broad and poorly structured maxima. Despite the poor structuring of the diffraction diagrams of liquids, certain statements can be made, at least in the short-range range within a cluster . Distance vectors of the particles, i.e. statements about distances and directions, cannot be determined via the intensity distribution, as in a crystal, only their amounts. A distance statistic is obtained which describes a distribution function of the pair distances. In this respect it is a problem to derive a three-dimensional structure. Via indirect methods, however, with structural models and their calculated distance statistics and a comparison with the experimental pair distribution function, statements about a possible structure can be made. It was possible to draw conclusions about liquid water from the X-ray structure investigation of the hexagonal ice with a β-tridymite structure. A hexagonal structural model gave good agreement with the experimental data, so that a β-tridymite structure was also assumed in water clusters. For example, resulted X-ray studies of an aqueous cesium fluoride solution to the conclusion that in the hydration of these cesium ions intercalate into the β-tridymite structure of the water clusters.
As early as the late 1920s, X-ray diffraction with liquids was performed by Peter Debye , Frits Zernike, and others. A determination of structures in the local area was not yet possible with the aids at that time due to the high computing effort and only became interesting with the use of computers.
literature
- Herbert Zimmermann: X-ray structure investigation of liquids . In: Chemistry in our time , 9th year 1975, No. 4, pp. 99-107.
- Walter Borchardt-Ott: Crystallography: an introduction for natural scientists . Verlag Springer, Berlin 1997, ISBN 3-540-63044-9 .
- Werner Massa: Crystal structure determination . Verlag Teubner, Stuttgart 2002, ISBN 3-519-23527-7 .
- Rudolf Allmann : X-ray powder diffractometry . Verlag Springer, Berlin 2003, ISBN 3-540-43967-6 .
- E. Prince (Ed.): International Tables for Crystallography (third series). Volume C. Mathematical, physical and chemical tables . 3. Edition. Springer, 2004, ISBN 978-1-4020-1900-5 ( limited preview in Google book search).
- Lothar Spieß, Gerd Teichert, Robert Schwarzer, Herfried Behnken, Christoph Genzel: Modern X-ray diffraction: X-ray diffractometry for materials scientists, physicists and chemists . 3. Edition. Springer Spectrum, Wiesbaden 2019, ISBN 978-3-8348-1219-3 , pp. 635 ( limited preview in Google Book search).
Web links
- LP - X-ray diffraction (including sketches, photos, videos and references)
- Fundamentals of X-ray diffractometry (XRD) and X-ray powder diffractometry (XRPD) (PDF, 2.7 MB)
Individual evidence
- ↑ Wolfgang Neumann, Klaus-Werner Benz: Crystals Change Our World Structure - Properties - Applications . Walter de Gruyter GmbH & Co KG, 2018, ISBN 978-3-11-043907-6 , p. 65 ( limited preview in Google Book search).
- ↑ Horst Biermann, Lutz Krüger: Modern methods of material testing . John Wiley & Sons, 2014, ISBN 978-3-527-67070-3 , pp. 255 ( limited preview in Google Book search).
- ↑ Lothar Spieß, Robert Schwarzer, Herfried Behnken, Gerd Teichert: Modern X-ray diffraction X-ray diffractometry for materials scientists, physicists and chemists . Springer-Verlag, 2015, ISBN 978-3-663-10831-3 ( limited preview in Google book search).
- ↑ Ludwig Bergmann, Clemens Schaefer: Textbook of Experimental Physics - 6th solid . Walter de Gruyter, 2005, ISBN 978-3-11-017485-4 , p. 112 ( limited preview in Google Book search).
- ↑ Kossel effect in the technology dictionary
- ^ WH Bragg , WL Bragg : The Reflection of X-rays by Crystals . In: Proceedings of the Royal Society of London. Series A . tape 88 , no. 605 , January 7, 1913, p. 428-438 , doi : 10.1098 / rspa.1913.0040 .
- ↑ Peter Debye , Paul Scherrer : Interferences on randomly oriented particles in X-ray light. I. In: Nachr. Ges. Wiss. Göttingen, mathematical-physical class. 1916, pp. 1-15.
- ↑ Peter Debye , Paul Scherrer : Interferences on randomly oriented particles in X-ray light. II. In: Nachr. Ges. Wiss. Göttingen, mathematical-physical class. 1916, pp. 16-26.
- ↑ Michael Polanyi , Ernst Schiebold , Karl Weissenberg : on the development of the rotary crystal process . In: Journal of Physics . tape 23 , no. 1 , December 1924, p. 337-340 , doi : 10.1007 / BF01327599 .
- ^ Diffraction techniques in the solid state . ( Memento of the original from October 3, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 930 kB) Lecture notes, University of Lethbridge.
- ^ Karl Weissenberg : A new X-ray goniometer . In: Journal of Physics . tape 23 , no. 1 , December 1924, p. 229-238 , doi : 10.1007 / BF01327586 .
- ↑ Erwin Sauter: A simple universal camera for X-ray crystal structure analysis . In: Journal of Crystallography . tape 85 , 1933, pp. 156-159 .
- ↑ Ernst Schiebold : About a new X-ray goniometer. Simultaneously a comment on the work of E. Sauter; "A simple universal camera for X-ray crystal structure analysis" . In: Journal of Crystallography . tape 86 , 1933, pp. 370-377 and 377-383 .
- ^ W. Bronger: Roentgenographic examinations according to the powder method. Document by the Institute for Inorganic Chemistry at RWTH Aachen University in 1971.
- ^ W. Kleber: Introduction to crystallography. VEB Verlag Technik Berlin 1969, p. 344.















![F _ {{hkl}} = \ int _ {0} ^ {a} \ int _ {0} ^ {b} \ int _ {0} ^ {c} \ rho (x, y, z) \, \ exp \ left [2 \ pi i \ left ({\ frac {hx} {a}} + {\ frac {ky} {b}} + {\ frac {lz} {c}} \ right) \ right] \, {\ mathrm {d}} x \, {\ mathrm {d}} y \, {\ mathrm {d}} z](https://wikimedia.org/api/rest_v1/media/math/render/svg/74099e8cf593081b62b20eadd8236eab9db4c979)




![F _ {{hkl}} = \ sum _ {j} ^ {N} f_ {j} \ exp [2 \ pi i (hx_ {j} + ky_ {j} + lz_ {j})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9e5e3d115a89d94d213fc0b522f41067e34f86e)







